Para verificar las ecuaciones de Einstein, debes patear un agujero negro

Dos equipos de investigadores han logrado un progreso significativo al probar la hipótesis de la estabilidad de los agujeros negros, la prueba matemática más importante de la Teoría general de la relatividad de Einstein.

En noviembre de 1915, en una conferencia en la Academia de Ciencias de Prusia, Albert Einstein describió una idea que convirtió a la humanidad en todo el universo. En lugar de fijar la geometría del espacio y el tiempo, Einstein explicó que vivimos en una realidad tetradimensional llamada espacio-tiempo, cuya forma fluctúa en respuesta a la materia y la energía.

Einstein describió esta importante idea en detalle en varias ecuaciones llamadas " ecuaciones de Einstein " (o ecuaciones del campo gravitacional) que forman el núcleo de su GTR. Esta teoría fue confirmada por todas las pruebas experimentales a las que fue sometida en el próximo siglo.

Y aunque la teoría de Einstein parece describir el mundo observado, las matemáticas subyacentes siguen siendo en gran parte misteriosas. Los matemáticos pudieron proporcionar muy poca evidencia con respecto a las ecuaciones mismas. Sabemos que funcionan, pero no podemos decir exactamente por qué. Incluso Einstein tuvo que regresar a aproximaciones, y no a soluciones exactas, para ver el Universo a través de las lentes que creó.

Pero durante el año pasado, los matemáticos han enfocado las matemáticas GR en un enfoque más claro. Dos grupos propusieron soluciones relacionadas con un problema importante en GR, conocido como la hipótesis de la estabilidad del agujero negro. Su trabajo demuestra que las ecuaciones de Einstein corresponden a la intuición física para el comportamiento del espacio-tiempo: si le aplicas una perturbación aguda, se sobresaltará como gelatina, y luego se calmará en un estado estable, a partir del cual todo comenzó.

“Si las decisiones fueran inestables, significaría que no son físicas. Sería un fantasma matemático que existe en las matemáticas, pero no importa desde el punto de vista de la física ", dijo Sergiu Kleinerman , matemático de la Universidad de Princeton, y autor, junto con Jeremy Szeftel , de uno de los dos resultados .

Para completar las pruebas, los matemáticos necesitaban resolver la complejidad básica de las ecuaciones de Einstein. Para describir la evolución de la forma espacio-tiempo, necesita un sistema de coordenadas, algo así como líneas de latitud y longitud, que le indique dónde están algunos puntos. Y en el espacio-tiempo es muy difícil encontrar un sistema de coordenadas que funcione en todas partes.

Sacude el agujero negro

Como saben, GR describe el espacio-tiempo como algo así como una lámina de goma. En ausencia de materia, la hoja es plana. Comience a arrojarle bolas (estrellas y planetas) y la hoja se deformará. Las bolas ruedan una hacia la otra. Cuando los objetos se mueven, la forma de la lámina de goma también cambia en respuesta.

Las ecuaciones de Einstein describen la evolución de la forma espacio-temporal. Les das información sobre la curvatura y la energía en cada punto, y dan la forma del espacio-tiempo en el futuro. En este sentido, las ecuaciones de Einstein son similares a las ecuaciones que simulan un fenómeno físico: aquí la pelota está en el tiempo cero, y aquí, después de cinco segundos.

"Esta es una versión cuantitativa matemáticamente precisa de la afirmación de que el espacio-tiempo está curvado en presencia de materia", dijo Peter Hinz, investigador del Clay Institute of Mathematics de la Universidad de California en Berkeley, responsable del segundo resultado con Andras Vasya.

En 1916, casi inmediatamente después del lanzamiento de GTR, el físico alemán Karl Schwarzschild encontró una solución exacta a las ecuaciones que describen lo que ahora conocemos con el nombre de un agujero negro (este término apareció solo cinco décadas después ). Más tarde, los físicos encontraron soluciones exactas que describen un agujero negro giratorio y BH con una carga eléctrica.

Y todas estas son decisiones exactas que describen BH. Si agrega al menos un segundo BH, la interacción de las fuerzas se vuelve tan complicada para las matemáticas modernas que solo se enfrenta en casos muy especiales.

Sin embargo, aún podemos hacer preguntas importantes sobre este grupo limitado de soluciones. Una de esas preguntas surgió en 1952 como resultado del trabajo de la matemática francesa Yvonne Choquet-Bruhat. De hecho, suena así: ¿qué sucede si sacudes un agujero negro?


Si sacudes el BH, creará ondas gravitacionales. Probar la hipótesis de la estabilidad es lo mismo que demostrar que estas ondas se dispersan en el vacío, como las ondas en la superficie de un estanque después de que cae una piedra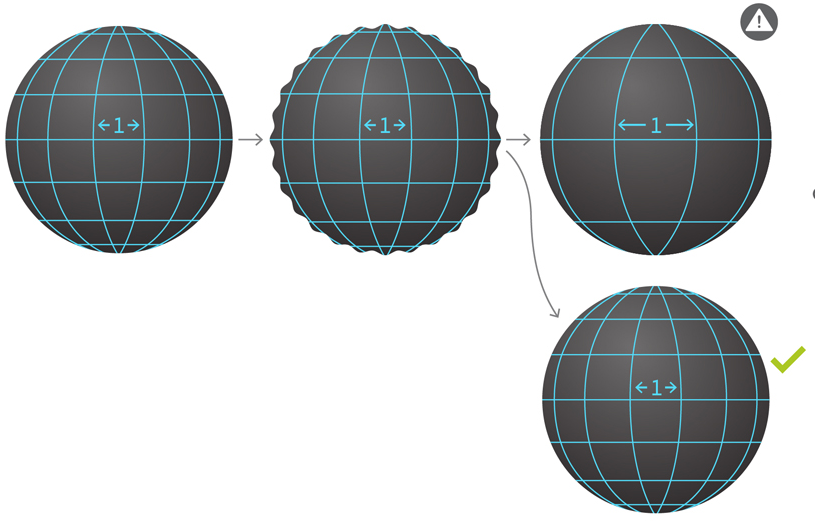


El espacio-tiempo cambia con el tiempo, y la cuadrícula utilizada para medir las ondas amortiguadas cambia con él. La plantilla determina los cambios en la cuadrícula y debe seleccionarse correctamente. Supongamos que tenemos un espacio-tiempo con una cuadrícula de 1 cm asociada con cierto patrón. Perturbaremos el espacio-tiempo para que aparezcan ondas gravitacionales. Un patrón seleccionado incorrectamente puede hacer que las distancias de la cuadrícula cambien, y parecerá que las ondas no se atenúan. El patrón correcto es crucial para medir el retorno a la sostenibilidad.

Este problema se conoce como hipótesis de estabilidad BH. Ella predice que las soluciones a las ecuaciones de Einstein serán "estables bajo disturbios". Hablando informalmente, si golpeas el BH, entonces el espacio también se volverá más caro y luego, en toga, se calmará de una forma que se verá muy similar a la que comenzamos. "En términos generales, la sostenibilidad significa que si tomamos soluciones especiales y las indignamos un poco, cambiamos los datos, la dinámica final estará muy cerca de la solución original", dijo Kleinerman.

La llamada "estabilidad" es una prueba importante de cualquier teoría física. Para comprender esto, sería útil presentar un ejemplo que sea más familiar que BH.

Imagina un estanque. Ahora imagine que ha rebelado su superficie arrojando una piedra allí. El estanque está un poco agitado, y luego se calmará. Matemáticamente, las soluciones de las ecuaciones utilizadas para describir el estanque (en este caso, las ecuaciones de Navier-Stokes ) deberían describir esta imagen física básica. Si la solución original no coincide con la decisión en un futuro lejano, puede que se pregunte sobre la exactitud de sus ecuaciones.

"Una ecuación puede tener propiedades, puede ser matemáticamente correcta, pero si contradice las expectativas físicas, no puede ser correcta", dijo Vasya.


Peter Hinz, matemático de la Universidad de California

Para los matemáticos que trabajan en las ecuaciones de Einstein, la prueba de estabilidad fue aún más difícil de encontrar que las soluciones a las ecuaciones mismas. Considere el caso de un espacio plano de Minkowski, la más simple de todas las configuraciones de espacio-tiempo. Esta solución de las ecuaciones de Einstein fue descubierta en 1908, en el contexto de la teoría especial de la relatividad anterior de Einstein. Pero solo en 1993, los matemáticos pudieron demostrar que si sacudes el espacio-tiempo plano y vacío, nuevamente obtienes el espacio-tiempo plano y vacío. Este resultado, obtenido por Kleinermann y Demetrios Christodoulou, es un trabajo venerado en esta área.

Una de las principales dificultades con la prueba de estabilidad está asociada con el seguimiento de lo que sucede en el espacio-tiempo de cuatro dimensiones durante la evolución de una solución. Necesita un sistema de coordenadas que le permita medir distancias y determinar puntos en el espacio-tiempo, como las líneas de latitud y longitud, que se utilizan para determinar una ubicación en la Tierra. Pero no es fácil encontrar un sistema de coordenadas que funcione en cada punto en el espacio de tiempo y continúe funcionando cuando cambia la forma del espacio-tiempo.

"No sabemos cómo hacer esto, adecuado para todos los casos", dijo Hinz en un correo electrónico. "El universo no nos da un sistema de coordenadas preferido".

Problema de medición

Lo primero que hay que entender sobre los sistemas de coordenadas es que las personas los inventaron. El segundo: no todos los sistemas de coordenadas le permiten definir todos los puntos en el espacio.

Tome la latitud y la longitud: pueden asignarse arbitrariamente. Los cartógrafos podrían elegir cualquier línea imaginaria como meridiano principal. Y aunque la latitud y la longitud ayudan a determinar casi cualquier lugar en la Tierra, ya no tienen sentido en los polos norte y sur. Si no sabía nada sobre la Tierra y solo tenía lecturas de latitud y longitud en sus manos, podría concluir incorrectamente que algo topológicamente incorrecto está sucediendo en estos puntos.

Esta posibilidad, sacar conclusiones incorrectas sobre las propiedades del espacio físico debido a la insuficiencia del sistema de coordenadas que lo describe, es la esencia de por qué es tan difícil demostrar la estabilidad del espacio-tiempo.

"Puede ser que exista estabilidad, pero usamos coordenadas inestables y, por lo tanto, omitimos la verdad de la estabilidad", dijo Michalis Dafermos, matemático de la Universidad de Cambridge, especialista líder en el estudio de las ecuaciones de Einstein.

En el contexto de la teoría de la estabilidad de un agujero negro, cualquier sistema de coordenadas utilizado debe desarrollarse de la misma manera que la forma del espacio-tiempo, como un guante cómodo que se adapta para cambiar la forma de la mano. La correspondencia entre el sistema de coordenadas y el espacio-tiempo debe ser buena al principio y permanecer así todo el tiempo. Si esto no es así, entonces pueden suceder dos cosas que interfieren con los intentos de demostrar la existencia de estabilidad.


Sergiu Kleinerman, matemático de la Universidad de Princeton

En primer lugar, su sistema de coordenadas puede cambiar de forma, lo que se romperá en ciertos puntos, al igual que la latitud y la longitud dejan de funcionar en los polos. Dichos puntos se denominan "singularidades coordinadas" (para distinguirlas de las singularidades físicas, por ejemplo, agujeros negros). Estos son puntos indefinidos en el sistema de coordenadas que no permiten describir completamente el desarrollo de la solución hasta el final.

En segundo lugar, un sistema de coordenadas mal seleccionado puede ocultar el fenómeno físico que debería medir. Para demostrar que las soluciones de las ecuaciones de Einstein llegan a un estado de calma después de las perturbaciones, los matemáticos necesitan monitorear cuidadosamente las ondas del espacio-tiempo causadas por las perturbaciones. Para entender por qué esto es necesario, vale la pena volver a la analogía con el estanque. Una piedra arrojada a un estanque genera olas. La estabilidad a largo plazo del estanque se debe al hecho de que las olas se debilitan con el tiempo: se vuelven cada vez más pequeñas, hasta que no hay rastros de su presencia.

La situación es similar al espacio-tiempo. La perturbación causará una cascada de ondas gravitacionales, y para demostrar la estabilidad es necesario demostrar que estas ondas están atenuadas. Y para esto, se necesita un sistema de coordenadas, o "cuadrícula", para medir el tamaño de las ondas. La cuadrícula correcta permite a los matemáticos ver cómo las ondas se aplanan y eventualmente desaparecen para siempre.

"La atenuación debe medirse en relación con algo, y aquí es donde entra el problema de la red", dijo Kleinerman. "Si tomamos la cuadrícula equivocada, incluso si la estabilidad está presente, esto no se puede probar, ya que la cuadrícula no me mostrará atenuación". Y si no calcula la tasa de atenuación de las olas, es imposible demostrar la estabilidad ".

El problema es que, aunque el sistema de coordenadas es extremadamente importante, no es obvio qué sistema elegir. "Hay demasiada libertad para elegir las condiciones para esta cuadrícula", dijo Hinz. "Y la mayoría de las opciones resultarán incorrectas".

En camino a la meta

Una prueba completa de la estabilidad de los agujeros negros requiere la prueba de que todas las soluciones conocidas de las ecuaciones de Einstein para BH (con el giro del agujero negro dentro de ciertos límites) son estables después de la perturbación. Entre las soluciones conocidas se encuentran la solución Schwarzschild que describe el espacio-tiempo de un BH no giratorio, y la familia de soluciones Kerr que describe la configuración espacio-tiempo en la que no hay nada más que un BH giratorio (y las propiedades de este BH - masa y momento angular - difieren dentro de la familia de soluciones) .

Ambos nuevos resultados han avanzado parcialmente hacia la prueba de una hipótesis completa.

Hinz y Washi, en un artículo publicado en arxiv.org en 2016, demostraron que los agujeros negros que giran lentamente son estables. Pero su trabajo no cubre BHs que giran a una velocidad mayor que cierto umbral.

Además, su evidencia tiene varios supuestos sobre la naturaleza del espacio-tiempo. La hipótesis original tuvo lugar en el espacio Minkowski, que no solo es plano y vacío, sino que también tiene un cierto tamaño. La prueba de Hintz y Vasya tiene lugar en el espacio de Sitter, donde el espacio-tiempo con aceleración crece hacia afuera, como en el Universo real. Cambiar la escena simplifica el problema desde un punto de vista técnico, y esto se puede entender por analogía: si arrojas una piedra a un estanque en expansión, la expansión estirará las olas y se debilitarán más rápido que si el estanque no se expandiera.

"Estamos viendo un universo con expansión acelerada", dijo Hinz. "Hace la tarea un poco más fácil, porque este proceso diluye las ondas gravitacionales".

Kleinermann y Scheftel tienen una característica ligeramente diferente. Su prueba, cuya primera parte se publicó en noviembre pasado, tiene lugar en el espacio-tiempo de Schwarzschild, que está más cerca de la condición original y más compleja del problema. Demuestran la estabilidad de un BH no giratorio, pero no se refieren a las decisiones en las que gira. Además, prueban la estabilidad de BH solo para una clase estrecha de perturbaciones, aquellas en las que las ondas gravitacionales generadas son simétricas de cierta manera.

Ambos resultados presentan nuevas técnicas para seleccionar el sistema de coordenadas apropiado. Hinz y Vasi comienzan con una solución aproximada de ecuaciones basada en un sistema de coordenadas aproximado, y aumentan gradualmente la precisión de la respuesta, hasta llegar a soluciones exactas y coordenadas que se comportan bien. Kleinerman y Scheftel utilizan un enfoque más geométrico.

Ahora los dos equipos están tratando de construir una prueba de la hipótesis completa basada en sus métodos. Algunos expertos observadores creen que el día que funcione no está lejos.

"Realmente creo que ahora todo está en la etapa de dificultades técnicas", dijo Dafermos. "Resulta que para resolver este problema, ya no se requieren nuevas ideas". Hizo hincapié en que la prueba final puede ser ofrecida por cualquiera de los matemáticos que trabajan en el problema en este momento.

Durante cien años, las ecuaciones de Einstein sirvieron como una instrucción experimental confiable para el Universo. Ahora los matemáticos probablemente se están acercando a demostrar por qué funcionan tan bien.