Determinación de la densidad del gas a partir de los resultados de medición de presión y temperatura con sensores Arduino

Introduccion

La tarea de medir los parámetros de una mezcla de gases está muy extendida en la industria y el comercio. El problema de obtener información confiable al medir los parámetros del estado del medio gaseoso y sus características utilizando medios técnicos se resuelve mediante los procedimientos de medición adoptados en los estándares (MVI), por ejemplo, al medir el caudal y la cantidad de gases usando dispositivos de constricción estándar [1], o usando una turbina, medidores y medidores de flujo rotacionales y de vórtice [2].

El análisis periódico de gases nos permite establecer una correspondencia entre la mezcla analizada real y su modelo, según la cual los parámetros fisicoquímicos del gas se tienen en cuenta en el MVI: la composición de la mezcla de gases y la densidad del gas en condiciones estándar.
Además, el MVI tiene en cuenta las características termofísicas del gas: densidad en condiciones de funcionamiento (presión y temperatura del gas en el que se mide su caudal o volumen), viscosidad, factor y factor de compresibilidad.

Los parámetros del estado del gas medidos en tiempo real incluyen: presión (presión diferencial), temperatura, densidad. Para medir estos parámetros, respectivamente, se utilizan medios de equipos de medición: manómetros (manómetros diferenciales), termómetros, densitómetros. La medición de la densidad del medio gaseoso puede medirse por métodos de medición directos o indirectos. Los resultados de los métodos de medición directos e indirectos dependen del error de los instrumentos de medición y del error metodológico. En condiciones de funcionamiento, las señales de información de medición pueden verse afectadas por un ruido significativo, cuya desviación cuadrática media puede exceder el error instrumental. En este caso, una tarea urgente es el filtrado efectivo de las señales de información de medición.

Este artículo analiza el método de medición indirecta de la densidad del gas en condiciones de operación y estándar utilizando un filtro Kalman.

Modelo matemático para determinar la densidad del gas.

Pasemos a los clásicos y recordemos la ecuación de estado de un gas ideal [3]. Tenemos:

1. La ecuación de Mendeleev-Clapeyron: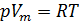

(1)

donde:

- presión de gas;

- volumen molar;

R es la constante de gas universal,

;

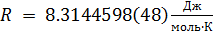
T es la temperatura absoluta, T = 273.16 K.

2. Dos parámetros medidos:

p - presión de gas, Pa
t es la temperatura del gas, ° C.

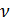
Se sabe que el volumen molar depende del volumen de gas V y la cantidad de moles de gas en este volumen:

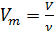
(2)

También se sabe que

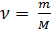
(3)

donde: m es la masa de gas, M es la masa molar de gas.

Dado (2) y (3) reescribimos (1) en la forma:

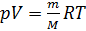
(4)

Como se sabe, la densidad de una sustancia

es igual a:

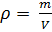
(5)

De (4) y (5) derivamos la ecuación para la densidad del gas

:

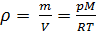
(6)

e introducir la notación para el parámetro

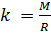
, que depende de la masa molar de la mezcla de gases:

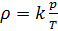
(7)

Si la composición de la mezcla de gases no cambia, entonces el parámetro k es constante.
Entonces, para calcular la densidad del gas, es necesario calcular la masa molar de la mezcla de gases.

La masa molar de una mezcla de sustancias se define como el promedio aritmético de la masa molar de las fracciones de masa incluidas en la mezcla de sustancias individuales.

Tomamos la composición conocida de sustancias en una mezcla de gases, en el aire, que consiste en:

• 23% en peso de moléculas de oxígeno
• 76% en peso de moléculas de nitrógeno
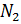
• 1% en peso de átomos de argón

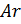
Las masas molares de estas sustancias atmosféricas serán respectivamente iguales a:

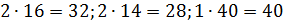
, g / mol.

Calculamos la masa molar del aire como el promedio aritmético ponderado:



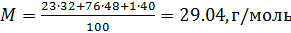
Ahora, sabiendo el valor de la constante

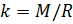
, podemos calcular la densidad del aire de acuerdo con la fórmula (7) teniendo en cuenta los valores medidos

y t :

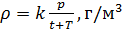
Llevando la densidad del gas a condiciones normales y estándar

En la práctica, las mediciones de las propiedades de los gases se llevan a cabo en diferentes condiciones físicas, y para garantizar la comparación entre diferentes conjuntos de datos, se deben establecer conjuntos de condiciones estándar [4].

Las condiciones estándar de temperatura y presión son las condiciones físicas establecidas por el estándar, con las cuales se correlacionan las propiedades de las sustancias que dependen de estas condiciones.

Varias organizaciones establecen sus condiciones estándar, por ejemplo: la Unión Internacional de Química Pura y Aplicada (IUPAC), ha establecido la definición de temperatura y presión estándar (STP) en el campo de la química: temperatura 0 ° C (273.15 K), presión absoluta 1 bar (Pa); El Instituto Nacional de Estándares y Tecnología (NIST) establece una temperatura de 20 ° C (293.15 K) y una presión absoluta de 1 atm (101.325 kPa), y este estándar se llama temperatura y presión normales (NTP); La Organización Internacional de Normalización (ISO) establece condiciones estándar para el gas natural (ISO 13443: 1996, confirmado en 2013): temperatura 15.00 ° y presión absoluta 101.325 kPa.

Por lo tanto, en la industria y el comercio es necesario indicar las condiciones estándar de temperatura y presión, con respecto a las cuales se realizan los cálculos necesarios.

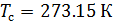
Calculamos la densidad del aire de acuerdo con la ecuación (8) en condiciones operativas de temperatura y presión. De acuerdo con (6), escribimos la ecuación para la densidad del aire en condiciones estándar: temperatura y presión absoluta :

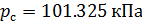
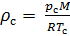
(9)

Hacemos el cálculo de la densidad del aire reducida a las condiciones estándar. Dividimos la ecuación (9) por la ecuación (6) y escribimos esta relación para :

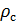
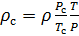
(10)

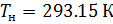
Del mismo modo, obtenemos una ecuación para calcular la densidad del aire reducida a condiciones normales: temperatura y presión absoluta

:

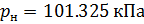
(11)

En las ecuaciones (10) y (11) usamos los valores de los parámetros del aire. , T y P de la ecuación (8) obtenida en condiciones de funcionamiento.

La implementación del canal de medición de presión y temperatura.

Para resolver muchas tareas de obtener información, dependiendo de su complejidad, es conveniente crear un prototipo de un sistema futuro basado en una de las plataformas de microcontroladores como Arduino, Nucleo, Teensy, etc.

¿Qué podría ser más fácil? Hagamos una plataforma de microcontrolador para resolver un problema específico: crear un sistema para medir la presión y la temperatura, gastar menos, posiblemente, fondos y utilizar todas las ventajas del desarrollo de software en el entorno del Software Arduino (IDE).

Para esto, a nivel de hardware, necesitaremos componentes:

1. Arduino (Uno, ...) - uso como programador;
2. microcontrolador ATmega328P-PU - microcontrolador de la futura plataforma;
3. un resonador de cuarzo de 16 MHz y un par de condensadores cerámicos de 12-22 pF cada uno (de acuerdo con las recomendaciones del fabricante);
4. un botón de reloj para reiniciar el microcontrolador y un pull-up más alimentación al pin RESET del microcontrolador 1 kOhm de resistencia;
5. BMP180 - transmisor de temperatura y presión con interfaz I2C;
6. convertidor de interfaz TTL / USB;
7. Consumibles: cables, soldadura, placa de circuito, etc.

Un diagrama esquemático de la plataforma, teniendo en cuenta las interfaces necesarias: una interfaz serial estándar, I2C, y nada más, se presenta en la Fig. 1)


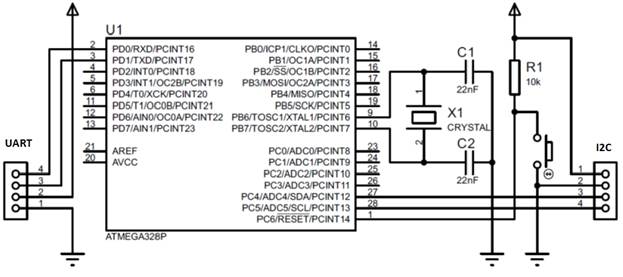Fig. 1 - Diagrama esquemático de una plataforma de microcontrolador para la implementación de un sistema de medición de presión y temperatura

Ahora consideraremos las etapas de la implementación de nuestra tarea.

1. Primero, necesitamos un programador. Conectamos Arduino (Uno, ...) a la computadora. En el entorno del software Arduno, desde el menú, vaya a Archivo-> Ejemplos-> 11. ArdunoISP llegamos al programador programador ArduinoISP, que cosimos en Arduino. Primero, en el menú Herramientas, seleccione respectivamente la placa, el procesador, el cargador y el puerto. Después de descargar el programa ArduinoISP a la placa, nuestro Arduino se convierte en un programador y está listo para usar para el propósito previsto. Para hacer esto, en el entorno del software Arduno, en el menú Herramientas , seleccione el elemento Programador: "Arduino como ISP ".

2. Conecte el microcontrolador esclavo ATmega328P a través de la interfaz SPI al programador maestro Arduino (Uno, ...), Fig. 2. Debe tenerse en cuenta que anteriormente los bits del registro de bytes de bajo fusible del microcontrolador ATmega328P estaban configurados en un estado no programado. Vaya al entorno de Arduno Software y, en el menú Herramientas , seleccione el elemento Grabar cargador . Destellando el microcontrolador ATmega328P.


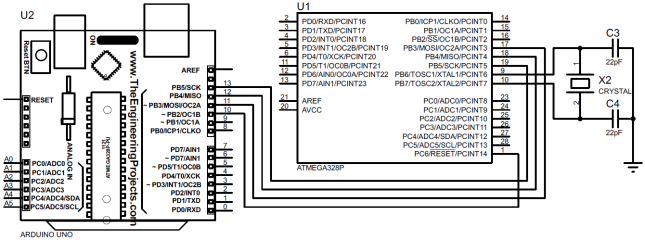Fig. 2 - Diagrama de conexión del microcontrolador al programador

3. Después de un firmware exitoso, el microcontrolador ATmega328P está listo para su instalación en la plataforma de microcontrolador desarrollada (Fig. 3), que es programable, así como el Arduino completo (Uno, ...). El programa de sondeo para el transmisor de presión y temperatura se muestra en el Listado 1.


Fig. 3 Sistema de medición de presión y temperatura.

Programa Python para filtrar por canales de temperatura y presión, y obtener resultados

El programa Python para el método para determinar la densidad del gas a partir de las mediciones de presión y temperatura se muestra en el Listado 2. La información del sistema de medición se muestra en tiempo real.


Los resultados del cálculo se presentan por listado y Fig. 4, 5, 6.



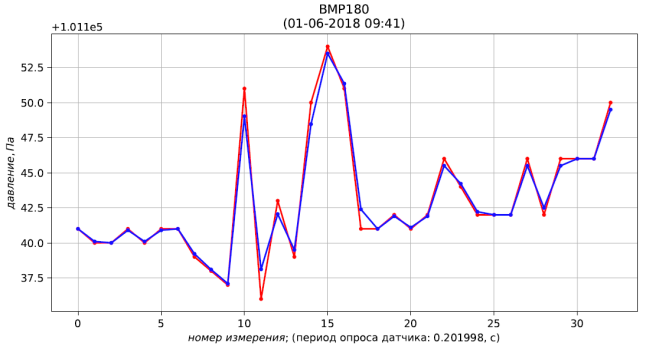Fig. 4 - resultados de medición (rojo) y filtración (azul) de presión


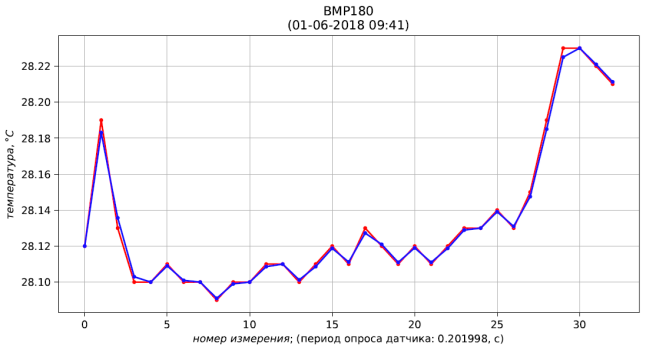Fig. 5 - resultados de medición (rojo) y filtración (azul) de temperatura


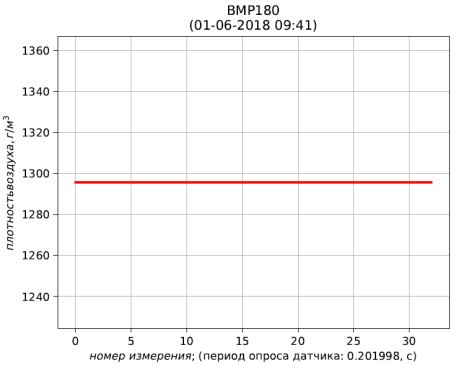Fig. 6 - resultados de cálculo de la densidad del aire reducida a condiciones estándar (temperatura 273.15 K; presión absoluta 101.325 kPa)

Conclusiones

Se ha desarrollado una técnica para determinar la densidad del gas a partir de mediciones de presión y temperatura utilizando sensores Arduino y el software Python.

Enlaces a fuentes de información.

1. GOST 8.586.5-2005. URL
2. GOST R 8.740 - 2011. URL
3. Ley del gas ideal. URL
4. Condiciones estándar de temperatura y presión. URL