Traducción de cómo las máquinas tienen sentido de Big Data: una introducción a los algoritmos de agrupamiento .Echa un vistazo a la imagen de abajo. Esta es una colección de insectos (los caracoles no son insectos, pero no encontraremos fallas) de varias formas y tamaños. Ahora divídalos en varios grupos según el grado de similitud. No hay trampa. Comience agrupando arañas.
Terminado? Aunque no hay una solución "correcta" aquí, debe haber dividido estas criaturas en cuatro
grupos . En un grupo hay arañas, en el segundo, un par de caracoles, en el tercero, mariposas, y en el cuarto, un trío de abejas y avispas.
Bien hecho, ¿verdad? Probablemente podría hacer lo mismo si hubiera el doble de insectos en la imagen. Y si tuviera mucho tiempo, o un ansia de entomología, entonces probablemente habría agrupado cientos de insectos.
Sin embargo, para una máquina, agrupar diez objetos en grupos significativos no es una tarea fácil. Gracias a una rama tan compleja de las matemáticas como la
combinatoria , sabemos que 10 insectos se agrupan de 115,975 formas. Y si hay 20 insectos, entonces el número de opciones de agrupación
superará los 50 billones .
Con un centenar de insectos, el número de posibles soluciones será mayor que el
número de partículas elementales en el Universo conocido . Cuanto mas Según mis estimaciones, unos
quinientos millones de billones de millones de veces más . Resulta más de
cuatro millones de billones de soluciones de
google (
¿qué es google? ). Y esto es solo para cientos de objetos.
Casi todas estas combinaciones no tendrán sentido. A pesar de la cantidad inimaginable de soluciones, usted mismo encontró rápidamente una de las pocas formas útiles de agrupamiento.
Los humanos damos por sentado nuestra excelente capacidad para catalogar y comprender grandes cantidades de datos. No importa si se trata de texto, imágenes en la pantalla o una secuencia de objetos: las personas, en general, entienden de manera efectiva los datos que provienen del mundo circundante.
Dado que un aspecto clave del desarrollo de IA y el aprendizaje automático es que las máquinas pueden comprender rápidamente grandes volúmenes de datos de entrada, ¿cómo puedo mejorar la eficiencia del trabajo? En este artículo, consideraremos tres algoritmos de agrupamiento con los que las máquinas pueden comprender rápidamente grandes cantidades de datos. Esta lista está lejos de ser completa, hay otros algoritmos, pero ya es bastante posible comenzar con ella.
Para cada algoritmo, describiré cuándo se puede usar, cómo funciona y también daré un ejemplo con análisis paso a paso. Creo que para una comprensión real del algoritmo, debe repetir su trabajo usted mismo. Si está
realmente interesado , se dará cuenta de que es mejor ejecutar algoritmos en papel. Acto, nadie te va a culpar!
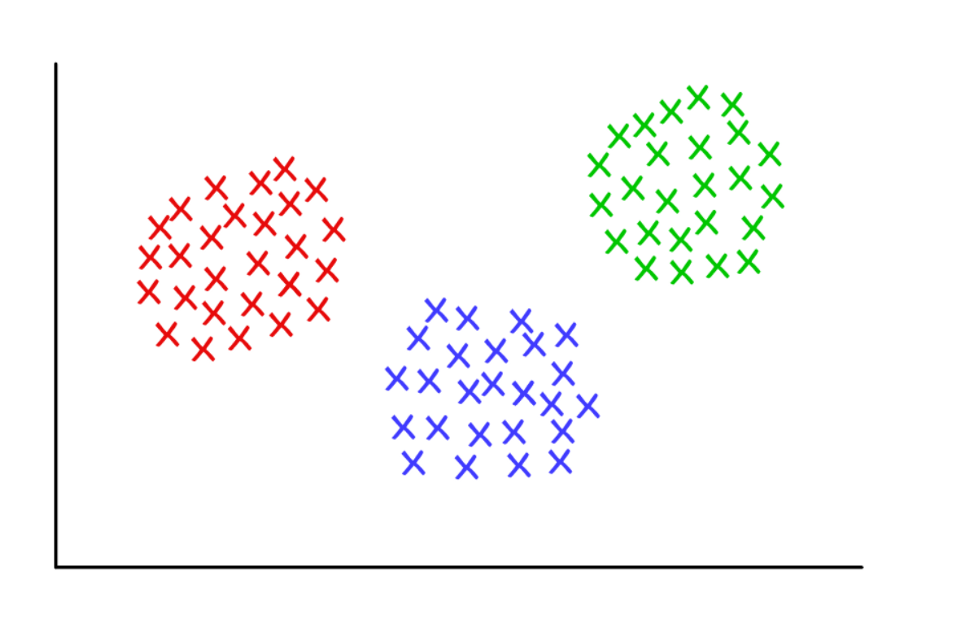Tres grupos sospechosamente limpios con k = 3K-significa agrupamiento
Utilizado por:
Cuando comprenda cuántos grupos se pueden obtener para encontrar
un predeterminado (a priori).
Cómo funciona
El algoritmo asigna aleatoriamente cada observación a una de las
k categorías y luego calcula el
promedio de cada categoría. Luego reasigna cada observación a la categoría con el promedio más cercano, y nuevamente calcula los promedios. El proceso se repite hasta que se necesiten reasignaciones.
Ejemplo de trabajo:
Tome un grupo de 12 jugadores y el número de goles marcados por cada uno de ellos en la temporada actual (por ejemplo, en el rango de 3 a 30). Dividimos a los jugadores, por ejemplo, en tres grupos.
Paso 1 : debes dividir aleatoriamente a los jugadores en tres grupos y calcular el promedio de cada uno de ellos.
Group 1 Player A (5 goals), Player B (20 goals), Player C (11 goals) Group Mean = (5 + 20 + 11) / 3 = 12 Group 2 Player D (5 goals), Player E (3 goals), Player F (19 goals) Group Mean = 9 Group 3 Player G (30 goals), Player H (3 goals), Player I (15 goals) Group Mean = 16
Paso 2 : reasigne a cada jugador al grupo con el promedio más cercano. Por ejemplo, el jugador A (5 goles) va al grupo 2 (promedio = 9). Luego nuevamente calculamos los promedios grupales.
Group 1 (Old Mean = 12) Player C (11 goals) New Mean = 11 Group 2 (Old Mean = 9) Player A (5 goals), Player D (5 goals), Player E (3 goals), Player H (3 goals) New Mean = 4 Group 3 (Old Mean = 16) Player G (30 goals), Player I (15 goals), Player B (20 goals), Player F (19 goals) New Mean = 21
Repita el paso 2 una y otra vez hasta que los jugadores dejen de cambiar de grupo. En este ejemplo artificial, esto sucederá en la próxima iteración.
Basta! ¡Has formado tres grupos a partir de un conjunto de datos!
Group 1 (Old Mean = 11) Player C (11 goals), Player I (15 goals) Final Mean = 13 Group 2 (Old Mean = 4) Player A (5 goals), Player D (5 goals), Player E (3 goals), Player H (3 goals) Final Mean = 4 Group 3 (Old Mean = 21) Player G (30 goals), Player B (20 goals), Player F (19 goals) Final Mean = 23
Los grupos deben corresponder a la posición de los jugadores en el campo: defensores, defensores centrales y delanteros. K-significa trabajar en este ejemplo porque hay razones para creer que los datos se dividirán en estas tres categorías.
Por lo tanto, en función de la variación estadística en el rendimiento, la máquina puede justificar la ubicación de los jugadores en el campo para cualquier deporte de equipo. Esto es útil para el análisis deportivo, así como para cualquier otra tarea en la que dividir el conjunto de datos en grupos predefinidos ayuda a sacar las conclusiones apropiadas.
Hay varias variaciones del algoritmo descrito. La formación inicial de grupos puede realizarse de varias maneras. Examinamos la clasificación aleatoria de jugadores en grupos, seguida del cálculo de promedios. Como resultado, los promedios iniciales del grupo están cerca uno del otro, lo que aumenta la repetibilidad.
Un enfoque alternativo es formar grupos que consisten en un solo jugador, y luego agrupar a los jugadores en los grupos más cercanos. Los grupos resultantes dependen más de la etapa inicial de formación, y la repetibilidad en conjuntos de datos con alta variabilidad disminuye. Pero con este enfoque, puede llevar menos iteraciones completar el algoritmo, ya que se dedicará menos tiempo a dividir los grupos.
El inconveniente obvio de la agrupación de k-means es que debe adivinar
de antemano cuántos grupos tiene. Existen métodos para evaluar la conformidad de un conjunto particular de grupos. Por ejemplo, la suma de cuadrados dentro del grupo es una medida de variabilidad dentro de cada grupo. Cuanto "mejores" son los grupos, menor es la suma total de cuadrados intragrupo.
Agrupación jerárquica
Utilizado por:
Cuando necesita revelar la relación entre los valores (observaciones).
Cómo funciona
La matriz de distancia se calcula en la que el valor de la celda (
i, j ) es la métrica de la distancia entre los valores de
i y
j . Luego se toma un par de los valores más cercanos y se calcula el promedio. Se crea una nueva matriz de distancia, los valores emparejados se combinan en un objeto. Luego se toma un par de los valores más cercanos de esta nueva matriz y se calcula un nuevo valor promedio. El ciclo se repite hasta que todos los valores estén agrupados.
Ejemplo de trabajo:
Tome un conjunto de datos extremadamente simplificado con varias especies de ballenas y delfines. Soy biólogo y puedo asegurarle que se utilizan muchas más propiedades para construir
árboles filogenéticos . Pero para nuestro ejemplo, nos restringimos a la longitud corporal característica de seis especies de mamíferos marinos. Habrá dos etapas de cálculos.
Paso 1 : se calcula la matriz de distancias entre todas las vistas. Utilizaremos la métrica euclidiana que describe qué tan lejos están nuestros datos unos de otros, como los asentamientos en el mapa. Puede obtener la diferencia en la longitud de los cuerpos de cada par leyendo el valor en la intersección de la columna y la fila correspondientes.
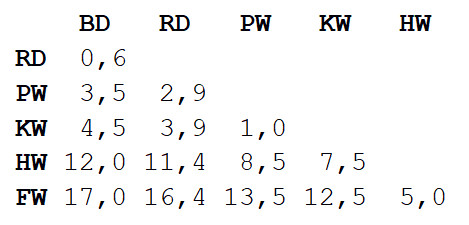Paso 2 : Tome un par de dos especies más cercanas entre sí. En este caso, se trata de un delfín nariz de botella y un delfín gris, en el que la longitud media del cuerpo es de 3,3 m.
Repetimos el paso 1, nuevamente calculando la matriz de distancia, pero esta vez combinamos delfín nariz de botella y delfín gris en un objeto con una longitud corporal de 3,3 m.
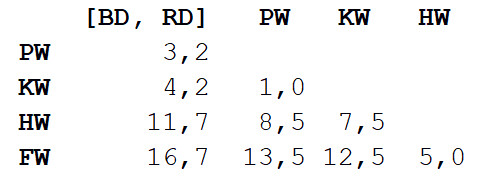
Ahora repetimos el paso 2, pero con una nueva matriz de distancia. Esta vez, la molienda y la orca serán las más cercanas, así que pongamos un par y calculemos el promedio: 7 m.
Luego, repita el paso 1: nuevamente, calcule la matriz de distancia, pero con la molienda y la orca en forma de un solo objeto con una longitud corporal de 7 m.
Repita el paso 2 con esta matriz. La distancia más pequeña (3.7 m) estará entre los dos objetos combinados, por lo que los combinaremos en un objeto aún más grande y calcularemos el valor promedio - 5.2 m.
Luego repita el paso 1 y calcule una nueva matriz combinando el delfín nariz de botella / delfín gris con la molienda / orca.
Repita el paso 2. La distancia más pequeña (5 m) será entre la jorobada y la aleta, por lo que las combinamos y calculamos el promedio - 17.5 m.
Nuevamente paso 1: calcule la matriz.
Finalmente, repita el paso 2: solo queda una distancia (12.3 m), por lo que uniremos a todos en un solo objeto y nos detendremos. Esto es lo que sucedió:
[[[BD, RD],[PW, KW]],[HW, FW]]
El objeto tiene una estructura jerárquica (recuerde
JSON ), por lo que se puede mostrar como un gráfico de árbol o dendrograma. El resultado es similar a un árbol genealógico. Cuanto más cerca estén dos valores en un árbol, más serán similares o estarán más estrechamente conectados.
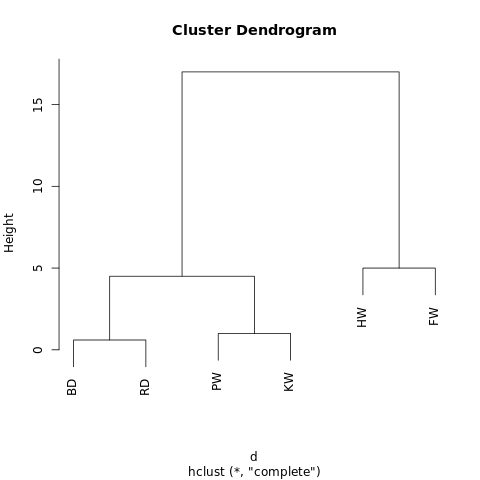Un dendrograma simple generado usando R-Fiddle.orgLa estructura del dendrograma le permite comprender la estructura del conjunto de datos en sí. En nuestro ejemplo, tenemos dos ramas principales: una con una jorobada y un finwal, la otra con un delfín nariz de botella / delfín gris y una orca.
En biología evolutiva, se utilizan conjuntos de datos mucho más grandes con muchas especies y una gran cantidad de caracteres para identificar las relaciones taxonómicas. Fuera de la biología, la agrupación jerárquica se aplica en las áreas de minería de datos y aprendizaje automático.
Este enfoque no requiere la predicción del número requerido de clústeres. Puede dividir el dendrograma resultante en grupos, "recortando" el árbol a la altura deseada. Puede elegir la altura de diferentes maneras, dependiendo de la resolución deseada de la agrupación de datos.
Por ejemplo, si el dendrograma anterior se corta a una altura de 10, entonces intersectaremos las dos ramas principales, dividiendo así el dendrograma en dos columnas. Si se corta a una altura de 2, luego divida el dendrograma en tres grupos.
Otros algoritmos de agrupamiento jerárquico pueden diferir en tres aspectos de los descritos en este artículo.
Lo más importante es el enfoque. Aquí usamos el método
aglomerativo : comenzamos con valores individuales y los agrupamos cíclicamente hasta que obtuvimos un gran grupo. Un enfoque alternativo (y computacionalmente más complejo) implica la secuencia inversa: primero se crea un gran grupo, y luego se divide secuencialmente en grupos cada vez más pequeños hasta que permanecen valores separados.
También hay varios métodos para calcular matrices de distancia. Las métricas euclidianas son suficientes para la mayoría de las tareas, pero
otras métricas son más adecuadas en algunas situaciones.
Finalmente, el criterio de vinculación puede variar. La relación entre grupos depende de su proximidad entre sí, pero la definición de "proximidad" puede ser diferente. En nuestro ejemplo, medimos la distancia entre los valores promedio (o "centroides") de cada grupo y combinamos los grupos más cercanos en pares. Pero puedes usar otra definición.
Supongamos que cada grupo consta de varios valores discretos. La distancia entre dos grupos puede definirse como la distancia mínima (o máxima) entre cualquiera de sus valores, como se muestra a continuación. Para diferentes contextos, es conveniente usar diferentes definiciones del criterio de unión.
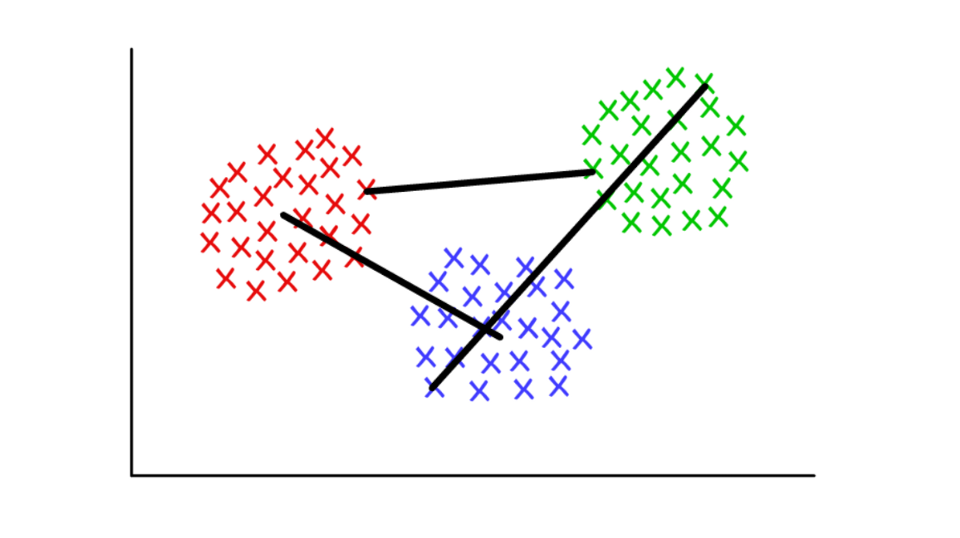Rojo / azul: grupo centroide; rojo / verde: combinación basada en mínimos; verde / azul: fusión basada en máximos.Definición de comunidades en gráficos (Detección de comunidad de gráficos)
Utilizado por:
Cuando sus datos pueden presentarse en forma de red o "gráfico".
Cómo funciona
Una comunidad en un gráfico puede definirse aproximadamente como un subconjunto de vértices que están más conectados entre sí que con el resto de la red. Existen diferentes algoritmos de definición de comunidad basados en definiciones más específicas, como Edge Betweenness, Modularity-Maximsation, Walktrap, Clique Percolation, Leading Eigenvector ...
Ejemplo de trabajo:
La teoría de grafos es una rama muy interesante de las matemáticas que nos permite modelar sistemas complejos en forma de conjuntos abstractos de "puntos" (vértices, nodos) conectados por "líneas" (bordes).
Quizás la primera aplicación de gráficos que viene a la mente es el estudio de las redes sociales. En este caso, los picos representan personas que están conectadas por costillas a amigos / suscriptores. Pero puede imaginar cualquier sistema en forma de red si puede justificar el método de conexión significativa de componentes. Las aplicaciones innovadoras de agrupamiento utilizando la teoría de grafos incluyen la extracción de propiedades de datos visuales y el análisis de redes reguladoras genéticas.
Como un simple ejemplo, veamos el gráfico a continuación. Esto muestra los ocho sitios que visito con más frecuencia. Los enlaces entre ellos se basan en enlaces en artículos de Wikipedia. Dichos datos se pueden recopilar manualmente, pero para proyectos grandes es mucho más rápido escribir un script Python. Por ejemplo, esto:
https://raw.githubusercontent.com/pg0408/Medium-articles/master/graph_maker.py .
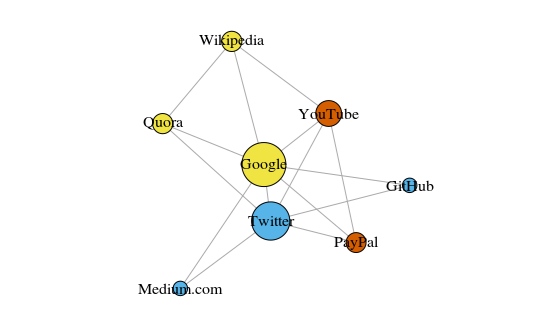El gráfico se construye usando el paquete igraph para R 3.3.3El color de los picos depende de la participación en las comunidades, y el tamaño depende de la centralidad. Tenga en cuenta que los más centrales son Google y Twitter.
Además, los grupos resultantes reflejan con mucha precisión tareas reales (esto siempre es un indicador importante de rendimiento). Los vértices que representan los enlaces / sitios de búsqueda están resaltados en amarillo; sitios resaltados en azul para publicaciones en línea (artículos, tweets o código); resaltados en rojo están PayPal y YouTube, fundados por ex empleados de PayPal. Buena deducción para la computadora!
Además de visualizar sistemas grandes, el verdadero poder de las redes reside en el análisis matemático. Comencemos convirtiendo la imagen de red en un formato matemático. La siguiente
es la matriz de
adyacencia de la red.
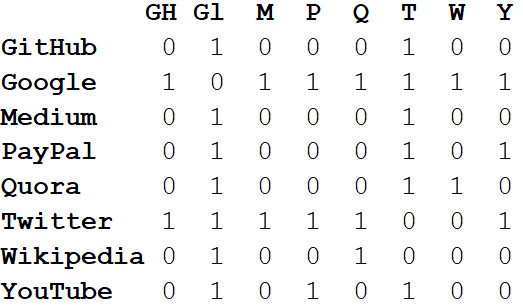
Los valores en las intersecciones de columnas y filas indican si hay un borde entre este par de vértices. Por ejemplo, entre Medium y Twitter está, por lo tanto, en la intersección de esta línea y la columna se encuentra 1. Y entre Medium y PayPal no hay borde, por lo que en la celda correspondiente hay 0.
Si representamos todas las propiedades de la red en forma de matriz de adyacencia, esto nos permitirá sacar todo tipo de conclusiones útiles. Por ejemplo, la suma de los valores en cualquier columna o fila caracteriza el
grado de cada vértice, es decir, el número de objetos conectados a este vértice. Generalmente indicado por la letra
k .
Si sumamos los grados de todos los vértices y los dividimos entre dos, obtenemos L, el número de aristas en la red. Y el número de filas y columnas es igual a N: el número de vértices en la red.
Conociendo solo k, L, N y los valores en todas las celdas de la matriz de adyacencia A, podemos calcular la modularidad de cualquier agrupación.
Supongamos que hemos agrupado una red en varias comunidades. Luego puede usar el valor de modularidad para predecir la "calidad" de la agrupación. Una mayor modularidad indica que dividimos la red en comunidades "exactas", y una menor modularidad sugiere que los grupos se forman más por casualidad que razonablemente. Para hacerlo más claro:
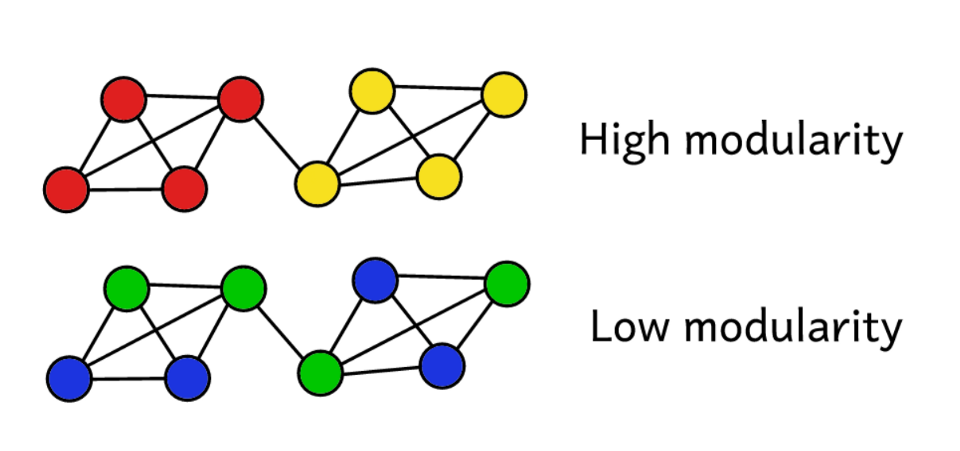
La modularidad sirve como una medida de la "calidad" de los grupos.
La modularidad se puede calcular utilizando la siguiente fórmula:
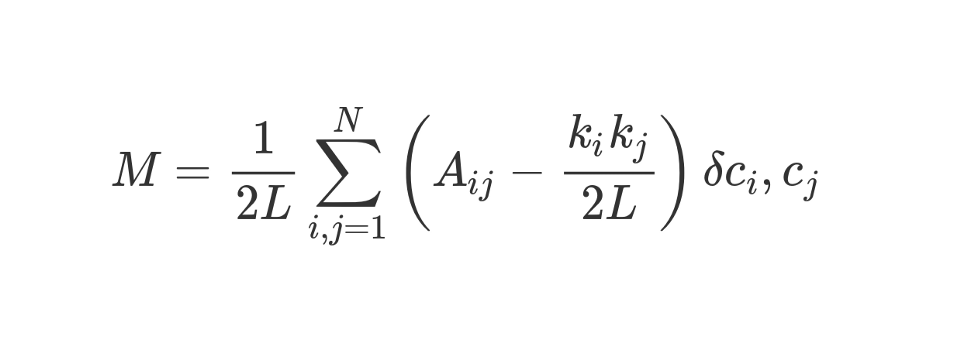
Veamos esta fórmula de aspecto increíble.
M , como sabes, esto es modularidad.
El coeficiente de
1 / 2L significa que dividimos el resto del "cuerpo" de la fórmula por 2L, es decir, por el doble número de aristas en la red. En Python, uno podría escribir:
sum = 0 for i in range(1,N): for j in range(1,N): ans =
¿Qué es
#stuff with i and j ? El bit entre paréntesis nos dice que restemos (k_i k_j) / 2L de A_ij, donde A_ij es el valor en la matriz en la intersección de la fila i y la columna j.
Los valores k_i y k_j son los grados de cada vértice. Se pueden encontrar sumando los valores en la fila i y la columna j, respectivamente. Si los multiplicamos y dividimos por 2L, obtenemos el número esperado de aristas entre los vértices i y j si la red se mezclara al azar.
El contenido de los corchetes refleja la diferencia entre la estructura real de la red y la esperada si la red se reconstruyera al azar. Si juegas con los valores, entonces la mayor modularidad estará en A_ij = 1 y baja (k_i k_j) / 2L. Es decir, la modularidad aumenta si hay un borde "inesperado" entre los vértices i y j.
Finalmente, multiplicamos el contenido de los corchetes por lo que se indica en la fórmula como δc_i, c_j. Esta es la función Kronecker-delta. Aquí está su implementación en Python:
def Kronecker_Delta(ci, cj): if ci == cj: return 1 else: return 0 Kronecker_Delta("A","A")
Si, muy simple. La función toma dos argumentos, y si son idénticos, devuelve 1, y si no, entonces 0.
En otras palabras, si los vértices i y j caen en un grupo, entonces δc_i, c_j = 1. Y si están en grupos diferentes, la función devolverá 0.
Como multiplicamos el contenido de los corchetes por el símbolo de Kronecker, el resultado de la suma invertida
Σ será el más alto cuando los vértices dentro de un grupo estén conectados por una gran cantidad de bordes "inesperados". Por lo tanto, la modularidad es un indicador de qué tan bien se agrupa un gráfico en comunidades individuales.
La división por 2L limita la modularidad superior a la unidad. Si la modularidad es cercana a 0 o negativa, esto significa que la agrupación actual de la red no tiene sentido. Al aumentar la modularidad, podemos encontrar una mejor manera de agrupar la red.
Tenga en cuenta que para evaluar la "calidad" de la agrupación de un gráfico, debemos determinar de antemano cómo se agrupará. Desafortunadamente, a menos que la muestra sea muy pequeña, debido a la complejidad computacional, es simplemente físicamente imposible pasar estúpidamente por todos los métodos de agrupar un gráfico comparando su modularidad.
Combinatorics sugiere que para una red con 8 vértices, hay 4.140 métodos de agrupamiento. Para una red con 16 vértices, ya habrá más de 10 mil millones de formas, para una red con 32 vértices, 128 septillones, y para una red con 80 vértices, la cantidad de métodos de agrupamiento excederá la
cantidad de átomos en el Universo observable .
Por lo tanto, en lugar de enumerar, usaremos el método heurístico, que ayudará a calcular relativamente fácilmente los clústeres con la máxima modularidad. Este es un algoritmo llamado
Fast-Greedy Modularity-Maximization , una especie de análogo al algoritmo de agrupamiento jerárquico aglomerativo descrito anteriormente. En lugar de combinar en base a la proximidad, Mod-Max une comunidades dependiendo de los cambios en la modularidad. Cómo funciona
Primero, cada vértice se asigna a su propia comunidad y se calcula la modularidad de toda la red: M.
Paso 1 : para cada par de comunidades conectadas por al menos un borde, el algoritmo calcula el cambio resultante en la modularidad ΔM en el caso de combinar estos pares de comunidades.
Paso 2 : luego se toma un par, cuando se combina, ΔM será máximo y se combinará. Para este agrupamiento, se calcula y almacena una nueva modularidad.
Se
repiten los pasos 1 y 2: cada vez que se une un par de comunidades, lo que da la mayor ΔM, un nuevo esquema de agrupamiento y su M.
Las iteraciones se
detienen cuando todos los vértices se agrupan en un gran grupo. Ahora el algoritmo verifica los registros almacenados y encuentra el esquema de agrupamiento con la mayor modularidad. Es ella quien regresa como una estructura comunitaria.
Fue computacionalmente difícil, al menos para las personas. La teoría de grafos es una rica fuente de problemas computacionales difíciles y problemas NP-difíciles. Usando gráficos, podemos sacar muchas conclusiones útiles sobre sistemas complejos y conjuntos de datos. Pregúntele a Larry Page, cuyo algoritmo PageRank, que ayudó a Google a transformarse de una startup a una posición dominante global en menos de una generación, se basa completamente en la teoría de gráficos.
Los estudios sobre teoría de grafos de hoy se centran en identificar comunidades. Hay muchas alternativas al algoritmo de maximización de modularidad, que, aunque útil, no está exento de inconvenientes.
Primero, con un enfoque aglomerativo, las comunidades pequeñas y bien definidas a menudo se combinan en comunidades más grandes. Esto se llama límite de resolución: el algoritmo no asigna comunidades más pequeñas que un cierto tamaño. Otro inconveniente es que, en lugar de un pico global pronunciado y fácilmente alcanzable, el algoritmo Mod-Max busca generar una "meseta" amplia a partir de muchos valores de modularidad cercanos. Como resultado, es difícil destacar al ganador.
Otros algoritmos utilizan diferentes métodos para definir comunidades. Por ejemplo, Edge-Betweenness es un algoritmo divisivo (divisorio) que comienza agrupando todos los vértices en un gran grupo. Luego, los bordes menos "importantes" se eliminan iterativamente hasta que se aíslan todos los vértices. El resultado es una estructura jerárquica en la que los vértices están más cerca uno del otro, cuanto más son similares.
El algoritmo, Clique Percolation, tiene en cuenta las posibles intersecciones entre comunidades. Hay un grupo de algoritmos basados en
una caminata aleatoria en un gráfico, y hay métodos de
agrupación espectral que se ocupan de la descomposición espectral (descomposición propia) de la matriz de adyacencia y otras matrices derivadas de ella. Todas estas ideas se utilizan para resaltar características, por ejemplo, en visión artificial.
No analizaremos ejemplos de trabajo para cada algoritmo en detalle. , , 20 .
Conclusión
, - , , . , , 20-40 .
, — , . , , .
, , , , . , - , , ? - !