Un artículo sobre el análisis del juego por una conocida red comercial despertó un
gran interés en
Cloud4Y . Aquí hay algunos pasajes para ponerte al día:
Una vez, en una soleada mañana de primavera, leyendo un foro de la ciudad, me encontré con un enlace con un juego simple de una conocida red comercial. El juego (acción) dedicado a la Copa del Mundo fue un campo sin complicaciones de tres por tres lleno de balones de fútbol. Al hacer clic en la pelota, abrimos una imagen con un producto en particular. Al abrir tres imágenes idénticas, se garantizó al participante un recibo gratuito de este producto en una de las tiendas de la red. Además, debajo de una de las bolas había una imagen de una tarjeta roja, cuya apertura significaba el final del juego.
El autor del artículo comenzó a investigar las razones de su pérdida y, basándose en los resultados de los cálculos, descubrió lo siguiente:
Un bosquejo rápido de las fórmulas en una servilleta, y resultó que la probabilidad de ganar es 1/4. Para 5 campos, tuve que jugar, pero la probabilidad calculada también fue del 25%.
...
Al ejecutar el script, obtuve un resultado inesperado: el 25% de las ganancias. Después de jugar con el número de elementos ganadores y el número total de campos, descubrí que la probabilidad de ganar en un juego de este tipo no depende del número de campos y es igual a uno dividido por el número de elementos ganadores aumentado en uno.
Estábamos interesados en la exactitud de tal cálculo y, reemplazando la servilleta con Excel, nos pusimos a trabajar en busca de la verdad matemática. Los lectores a quienes les gusta la teoría de la probabilidad están invitados a cat, para verificar la exactitud de nuestros cálculos.
En primer lugar, descubrimos las reglas del juego. En esto, sin saberlo, el usuario de Habr
Stecenko ayudó en su
comentario . Él también escribe:
Si miras el guión del autor, está escrito bajo el supuesto de que DEBE haber tres cartas de un producto en el campo, una carta de otros cinco bienes y una tarjeta roja, mientras que la descripción del juego no sigue absolutamente esto: las reglas no dicen que la combinación ganadora debe estar presente en el campo.
Las reglas, sin embargo, dicen que participan un total de 26 productos. Resulta que se genera la emisión de 9 tarjetas: 8 tarjetas son combinaciones de 26 productos con repeticiones, y una tarjeta es roja.
En tales condiciones, el cálculo de la probabilidad matemática de ganar es algo más complicado de lo que sugirió el autor de la publicación original. El juego consta de varias capas:- La probabilidad de abrir N cartas sin abrir la roja es la probabilidad de una duración diferente del juego, independientemente de si habrá un premio.
- La probabilidad de recoger una combinación de 3 cartas con los mismos bienes. Esta probabilidad varía con las diferentes duraciones del juego. Es importante entender que un conjunto de 8 cartas con productos y siempre una roja no contiene necesariamente al menos un par de cartas idénticas, sin mencionar tres a la vez.
Comencemos con una simple: comprender cómo disminuirá el número de participantes con el aumento en el número de tarjetas que abren debido a la regla de la tarjeta roja.
Probabilidades de diferentes duraciones de juego.
Calculamos la probabilidad de que para N intentos (cartas abiertas) se abra el rojo.UPD: Inicialmente, calculamos la probabilidad de abrir rojo usando una distribución binomial. Esto no nos garantizó estrictamente 1 tarjeta roja, con tal distribución probablemente hubo una tarjeta roja, pero podría haber 0 o los 9 con una probabilidad muy, muy pequeña. Nuevamente, gracias a Stecenko por señalar un error en el comentario y sugerir la solución correcta .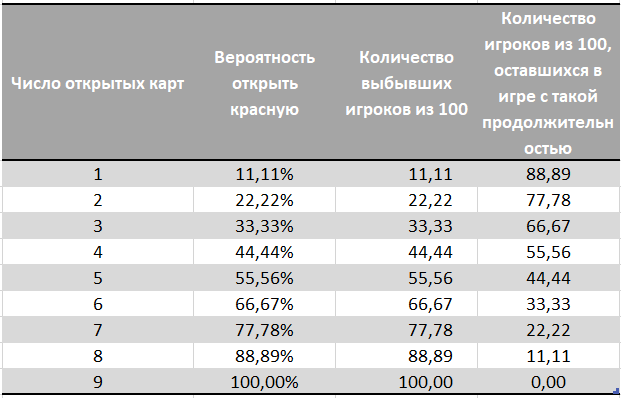
La última columna muestra cuántos jugadores de cada cien permanecen en el juego con esta duración. El resto de los jugadores son eliminados debido a la tarjeta roja, sin saber si hubo una combinación ganadora en el conjunto de tarjetas emitidas.
Ahora calcularemos las probabilidades de recolectar una combinación de tres cartas con los mismos bienes. Esta es una condición para recibir un premio.
Posibilidades de premios
Descomponemos el juego lógicamente. Abrimos la primera carta, y luego seleccionamos el par para esta carta, seleccionamos los tres para el par. Con este enfoque, podemos calcular la probabilidad de obtener 3 cartas idénticas en tres o más intentos, en función del hecho de que hay 26 productos en el juego.
Para tareas con un número fijo de pruebas o pruebas, si el resultado de cualquier prueba solo puede ser exitoso o fallido, las pruebas son independientes y la probabilidad de éxito permanece constante durante todo el experimento, usaremos la fórmula de Bernoulli, en Excel, la función BINOM.DIS.
Usando la función BINOM.RASP, puede calcular, por ejemplo, la probabilidad de que dos de los próximos tres recién nacidos sean niños. ¿Cuál es la probabilidad de descubrir tres de lo mismo en tres intentos?
= BINOM.RASP (3; 3; 1/26; 0) por máscara
= BINOM.DISP (número de éxitos; número de ensayos; probabilidad de éxito; integral)
O aquí está la fórmula para calcular la probabilidad de obtener 3
bienes idénticos y ciertos en 8 intentos.
= BINOM.RASP (3; 8; 1/26; 0), ¿verdad?
En realidad no Cuando alcanzamos la duración del juego en 4 intentos, sin permitir la apertura del rojo y continuar jugando, tenemos una situación con la posibilidad de que dos pares seleccionen un tres ganador.
Convencionalmente, dos productos de 26 son A y B. Nuestras tarjetas abiertas son A-B-A-B. La probabilidad ya no es 1/26, sino 1/26
+ (1/26) * "La probabilidad de dos pares para una duración determinada del juego" .
La probabilidad de dos pares para una duración determinada del juego = BINOM.DISP (2; 5; 1/26; 0) ^ 2
Cuando alcanzamos un juego más largo en el séptimo intento, obtenemos combinaciones como A-B-A-B-B-B. Esto significa que la probabilidad ahora es igual
= 1/26 * (1 + BINOM.RASP (2; 7; 1/26; 0) ^ 2 + BINOM.RASP (2; 7; 1/26; 0) ^ 3) y estamos buscando una tercera carta para 1, 2 o tres pares.
UPD: Además, inicialmente no tomamos en cuenta que el primer intento en nuestro cálculo de las ganancias, despejado de la probabilidad de elegir el rojo, es el descubrimiento de cualquiera de los 26 productos, lo que significa un 100% de éxito. El número de repeticiones de un producto en la matriz es el número de coincidencias con cualquier producto, lo que significa que dos repeticiones a un producto son suficientes para ganar, y no unir 3 con un resultado específico previsto. Por lo tanto, la primera opción de cualquier carta y dos intentos de recoger dos más de la misma forma un total de tres experimentos.Conociendo las probabilidades, estamos construyendo una matriz:
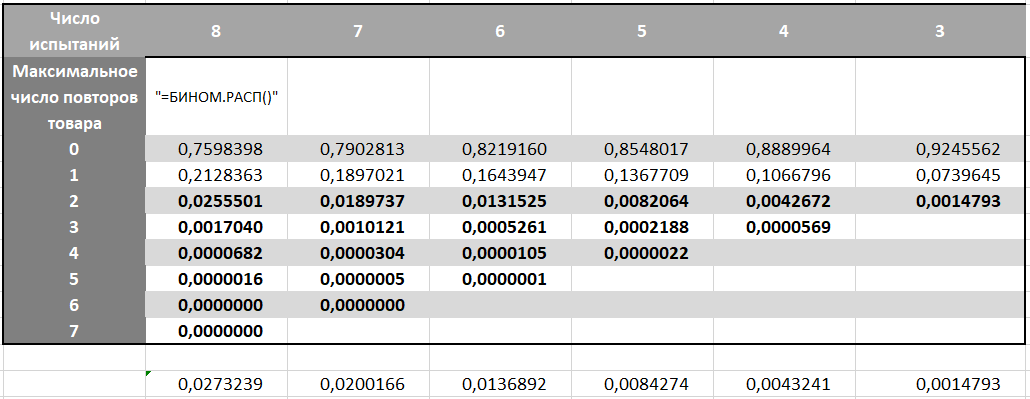
En él encontramos la probabilidad de cada número máximo de repeticiones de un producto para cada variante de la duración del juego. Recuerde que la probabilidad de ganar cambia en el cuarto intento y en el 7, lo que significa que tenemos esto en cuenta en la fórmula BINOM.RASP
Necesitamos opciones con un número máximo de repeticiones de cualquier producto de 3 o más. Dado que el juego se detendrá tan pronto como recolectemos los tres, agregamos las probabilidades por columnas en el área en negrita.
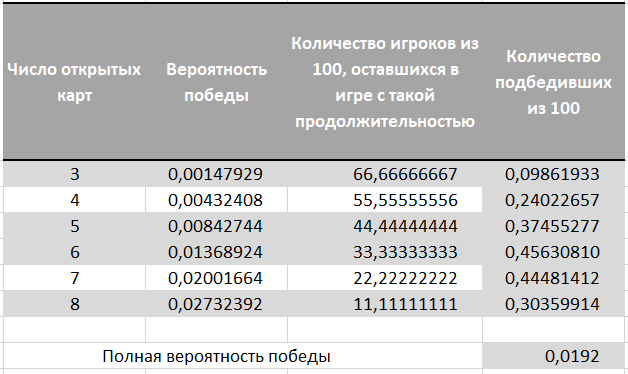
Luego, multiplicamos las posibilidades de la duración de cada juego por las posibilidades de ganar un premio con tal duración. Resumiendo estas piezas, tenemos una probabilidad de 0.0192 o 192 ganadores por cada 10,000 jugadores.
Sí, de hecho es una probabilidad muy baja. Nada del 25%. Veamos nuevamente las reglas del juego:
8. Fondo de premios:
8.1. Premios disponibles: nombres y cantidades
...
Total 166,000
Dividimos 116,000 por la probabilidad de ganar y obtenemos alrededor de 6 millones de participantes para poder jugar todos los premios. Recuerde que el 1 de enero de 2018, según Rosstat, había 146 938 921 residentes permanentes en Rusia. Aparentemente, esta es la idea de los organizadores del juego: dar la oportunidad de ganar a casi todos los ciudadanos de Rusia.UPD: la probabilidad final ha cambiado después de los cambios. Ahora podemos probar nuestros cálculos en la práctica con la ayuda de guiones, pero el don mental de Dios de los matemáticos y teóricos de generaciones anteriores es asombroso, quienes calcularon tantas probabilidades, encontrando la solución correcta en papel y usando experimentos mentales.El análisis del código mostró al autor de la publicación original que incluso antes del comienzo del juego, el guión "conoce" su resultado, pero nadie sabe qué resultado predeterminado dará el guión a un usuario específico. Conociendo el lado matemático del problema, podrá llegar a su propia conclusión sobre la honestidad de los organizadores.