Lógica difusa para controlar
El texto se basa en materiales del libro de V. Gostev. "Reguladores difusos en sistemas de modelado automático". Como todas las publicaciones serias sobre el tema, este libro está sobrecargado de cálculos matemáticos y es difícil para el lector no preparado. Mientras tanto, los principios de crear y usar la lógica difusa en sí mismos son bastante simples y claros. Este texto es un intento de traducir un ejemplo de un libro de un lenguaje matemático a uno de ingeniería.
Una posible secuencia de diseño de un controlador basado en lógica difusa se muestra complicando secuencialmente las reglas lógicas y seleccionando parámetros utilizando métodos de optimización.
Declaración del problema.
Considere la síntesis de un controlador PID digital y un controlador difuso para un sistema de control de misiles por ángulo de ataque. Utilizando modelos matemáticos, determinamos los procesos en el sistema y brindamos una evaluación comparativa de la calidad del sistema utilizando controladores sintetizados.
Tomando el ángulo de ataque como la coordenada de salida del misil:  y para la entrada coordine el ángulo de dirección
y para la entrada coordine el ángulo de dirección  defina la función de transferencia del cohete en la forma:
defina la función de transferencia del cohete en la forma:
 donde:
donde:
 - coeficiente de conversión de cohetes,
- coeficiente de conversión de cohetes,
 - coeficiente de amortiguación,
- coeficiente de amortiguación,
 - tiempo constante.
- tiempo constante.
En lo sucesivo, la "función de transferencia" no se utiliza en una definición clásica estricta, como la relación de las transformaciones de Laplace.
En el estudio del sistema de control, suponga que la dependencia de los parámetros del cohete en el tiempo de vuelo se determina de la siguiente manera:

Para simplificar los cálculos, describimos el mecanismo de dirección mediante la función de transferencia del enlace integrador  En este caso, la entrada del sistema
En este caso, la entrada del sistema  - ángulo de ataque dado, salida del sistema
- ángulo de ataque dado, salida del sistema  Es el ángulo de ataque elaborado por el cohete, m (t) es la señal de control a la salida del controlador, y el objeto de control se describe mediante la función de transferencia general:
Es el ángulo de ataque elaborado por el cohete, m (t) es la señal de control a la salida del controlador, y el objeto de control se describe mediante la función de transferencia general:

(El mecanismo de dirección analógico y el cohete están incluidos en el objeto de control).
La ley de variación de la acción de entrada viene dada por el polinomio:

Es necesario desarrollar un controlador que garantice el desarrollo del efecto de entrada utilizando un controlador PID y un controlador basado en lógica difusa.
Seleccionar los coeficientes de los reguladores.
Compare el transitorio con el controlador PID y el controlador basado en lógica difusa.
Modelo de objeto dinámico
Cree un modelo dinámico en un entorno de modelado estructural.
El circuito modelo en sí se muestra en la Figura 1.
La acción especificada se establece en forma de un bloque constante, una variable del script se establece como parámetros. Los parámetros de la función de transición se establecen en forma de variables.
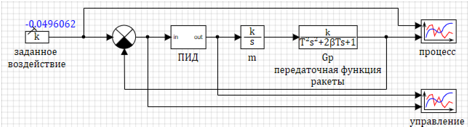 Figura 1. Diagrama de un modelo dinámico de un cohete.
Figura 1. Diagrama de un modelo dinámico de un cohete.Ajuste del regulador
El bloque PID es un submodelo (Fig. 2), que utiliza el bloque estándar "Controlador PID discreto". La frecuencia de muestreo se selecciona igual a 0.001 seg.
 Figura 2. Controlador PID con circuito de sintonización.
Figura 2. Controlador PID con circuito de sintonización.Los parámetros del controlador se configuran en forma de nombres de señales globales del proyecto
Kp, Ki, Kd. Esto le permite cambiar los parámetros durante la simulación y ajustar el regulador.
El bloque
"Optimización" se utilizó para ajustar el regulador, el criterio de optimización es la desviación estándar mínima.
La unidad de optimización lleva a cabo la optimización durante todo el proceso de transición. El resultado de la optimización es un vector de tres coeficientes, que se envía al bloque "Escribir en la lista de señales", donde los valores calculados se transfieren a las señales y, en consecuencia, los valores de los coeficientes PID cambian. Para configurar el controlador, establecemos los siguientes parámetros de optimización:
Valores iniciales de todos los coeficientes
1.El rango de selección se establece de
-50 a
+50Precisión de selección
0.001Desviación estándar máxima después de la optimización
0.01En este caso, la unidad de optimización calculó los siguientes valores óptimos de los coeficientes:
Kp = -1.7498597; Ki = 17.891995; Kd = 11.606602 .
Con estos coeficientes, la desviación estándar en el transitorio dado fue
0.008738090
Figura 3. Transitoria.
| 
Figura 4. Gestión. |
Controlador lógico difuso
Las principales ventajas de un controlador basado en lógica difusa son la simplicidad y la claridad de la formación de las reglas para controlar el objeto.
Por ejemplo, en el libro "Reguladores difusos en sistemas de modelado automático", las reglas de regulación difusa para controlar el cohete por el ángulo de ataque se describen en forma de una expresión matemática:

donde

- error del sistema, errores de cambio de velocidad (primera derivada), errores de aceleración (segunda derivada);
m - acción de control sobre el objeto;

- estimaciones lingüísticas de error, tasa de cambio de error (primera derivada) de error y segunda derivada de error, consideradas como conjuntos difusos definidos en un conjunto universal

;

- estimaciones lingüísticas de la acción de control sobre el objeto, seleccionadas de los conjuntos de términos de la variable
mEl lector puede preguntar: ¿cómo está, tu madre? Lo siento, ¿entiendes?
A veces me invaden dudas de que los matemáticos mismos entiendan lo que escribieron. Detrás de los turnos matemáticos abstrusos, se oculta el gran secreto de las reglas de regulación difusa. Aquí esta:
reducir mucho
norma - no tocar
pequeño - aumentarSi traduces del lenguaje de las matemáticas de las aves al ruso, entonces la expresión

literalmente significa lo siguiente:
Si es
más de lo normal y la
desviación aumenta y
la tasa de crecimiento aumenta , entonces
disminuimos .
Si la
norma no cambia y la
velocidad es constante , entonces
no cambiamos .
Si es
menos de lo normal y
cae y
la tasa de caída aumenta , entonces
aumente .
Si comprende lo que realmente está oculto detrás de la niebla matemática, puede abordar la creación de reguladores de manera más consciente y obtener resultados más interesantes.
Poco de teoría
Para resolver el problema de ajustar el ángulo de ataque, debemos obtener tres términos del valor de desviación continua: menos, norma, más. Lo mismo debe hacerse para la primera derivada de la desviación y la segunda derivada de la desviación. Esta es la primera etapa de la inferencia difusa: la fase.
Para obtener los términos, necesitamos establecer el valor numérico del parámetro para cada término. Por ejemplo: "Little" = -1; "Norma" = 0; "Many" = 1. Para la fase usaremos funciones triangulares. Las funciones crecen a medida que se acerca al valor establecido y disminuyen a medida que se aleja. En la Figura 5 se muestran dos opciones para funciones triangulares:

 Figura 5. Funciones de membresía triangular.
Figura 5. Funciones de membresía triangular.Conociendo la desviación (x1), podemos encontrar los valores de la función de membresía para los términos más (línea roja), norma (línea verde), menos (línea azul). Los valores variarán de 0 a 1.
Tenga en cuenta que en el gráfico de la izquierda las funciones extremas no son del todo "triangulares". Si lo consideramos desde el punto de vista de las matemáticas abstractas, entonces las funciones en el gráfico de la derecha son más "hermosas". Pero, si recuerda el "secreto principal de las reglas de la inferencia difusa", entonces el cuadro de la izquierda es más correcto. De hecho:
Considere la regla
"Agregar - pequeño" , si tenemos un valor de -1, entonces
"pequeño" = 1 (línea roja) es verdadero para ambos gráficos. ¿Y si tenemos un valor de -2? Lógicamente, también debemos
agregar . En el gráfico izquierdo en -2 es:
"little = 1" , pero en el gráfico derecho tenemos
"little" = 0, lo que obviamente no es cierto. Lo mismo es cierto para la regla
"reducir mucho" .
La eliminación gradual por funciones triangulares "honestas" puede llevar al hecho de que cuando el valor va más allá del rango de definición de funciones, obtenemos 0 para todos los términos, lo que, a su vez, puede conducir a la ausencia de impacto en el objeto.
El problema inverso es la desfasificación. Para calcular el impacto, debe realizar la transformación inversa: tenemos los valores de las funciones de membresía para reducir, no cambiar, aumentar el rango (
0 ... 1 ) (funciones triangulares) y el rango de efectos que podemos tener, y debemos obtener uno de los tres términos El número es un impacto específico.
Puede obtener el impacto de varias maneras, por ejemplo, en el centro de masa de la figura. La Figura 6 muestra el estado del controlador, donde los valores de los términos disminuyen
0.3 no cambian
0.6 y aumentan
0.8 con un rango de impacto regulatorio
-30..30 impacto resultante =
4.1.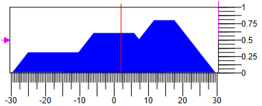 Figura 6. Desfazificación de la acción de control
Figura 6. Desfazificación de la acción de controlOtra opción para la desfazificación está en el centro de masa de los puntos. La Figura 7 muestra una opción donde, para los mismos valores de los términos y el rango de control, obtenemos otra respuesta
8.82 :
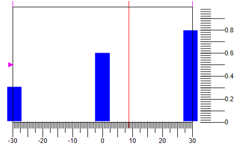 Figura 7. Desfazificación por el centro de masa de puntos.
Figura 7. Desfazificación por el centro de masa de puntos.Debe entenderse que, además del método de inferencia, la forma de la función de membresía también afecta el resultado. Por ejemplo, puede elegir tales funciones triangulares para las cuales la base del triángulo es la misma, solo difieren los vértices. (ver fig. 8).
 Figura 8. Funciones de pertenencia triangular con una base.
Figura 8. Funciones de pertenencia triangular con una base.En este caso, para reducir el resultado de la faseización con los mismos valores de los términos 0.3, no cambie 0.6 y aumente -0.8 con el rango de impacto regulatorio -30, 30 impacto resultante =
5.27 .
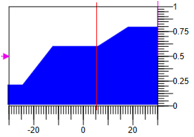 Figura 9. Desfazificación por cálculo de área.
Figura 9. Desfazificación por cálculo de área.Armados con el conocimiento secreto de la lógica difusa, crearemos un modelo de controlador. Dejamos el modelo de cohete igual que para el controlador PID (ver Fig. 1), pero en el submodelo del controlador ensamblamos el circuito que se muestra en la Figura 10.
 Figura 10. El circuito del controlador basado en lógica difusa.
Figura 10. El circuito del controlador basado en lógica difusa.En la entrada al regulador, se aplica un desajuste entre el ángulo de ataque dado y el real (medido). Después de la entrada hay un bloque "Extrapolador", que proporciona la conversión de una señal continua en una discreta con un período de muestreo dado (0.001 s es el mismo que el de un controlador PID discreto).
Después de esto, se calculan las desviaciones derivadas primera y segunda. Para hacer esto, calculamos la diferencia entre el valor actual y el valor con un retraso para el período de cuantificación, dividiéndolo por el tiempo de retraso (coeficiente en el bloque de comparación). Por lo tanto, obtenemos tres entradas: error del sistema, tasa de cambio (primera derivada) del error, aceleración (segunda derivada) del error.
El valor de las variables de entrada se convierte mediante bloques de fase en funciones triangulares. Para cada variable, obtenemos tres variables lingüísticas (nueve en total).
El demultiplexor bloquea los vectores de raza en variables lingüísticas para formar reglas. En el diagrama, los nombres de las variables se firman en el orden de su orden en los vectores.
La desviación en nuestro caso es la diferencia entre el conjunto y el medido, si un valor negativo significa que el ángulo de ataque es mayor que el conjunto, debemos reducirlo. Y en consecuencia, por el contrario, si la desviación es positiva, entonces el ángulo medido es menor que el especificado, debemos aumentarlo.
(Más - reducir, menos - aumentar, la norma - no tocar) .
La salida también tiene tres variables lingüísticas "reducir", "no cambiar", "aumentar". El multiplexor recoge los valores en un vector y lo envía al bloque de salida difusa. Ahora que tenemos todas las variables, podemos escribir las reglas de inferencia difusa en forma de diagrama.
- Si es más de lo normal y la desviación aumenta y la tasa de crecimiento aumenta => disminuye.
- Si la norma no cambia y es constante => no cambiamos.
- Si es menos de lo normal y cae y la tasa de caída aumenta => aumenta.
Todas las variables lingüísticas en las reglas están conectadas a través de los bloques lógicos "y" y conectadas a las salidas. Como se puede ver en la Figura 10, el circuito de inferencia difusa lógica prácticamente no es diferente del circuito lógico habitual, solo se utilizan bloques de lógica difusa.
De manera similar al ajuste del controlador PID, utilizamos el bloque de optimización.
La pregunta permanece con los parámetros de los bloques.
Síntesis de un controlador basado en lógica difusa
Nada se da en la vida por nada, y por lo tanto, la simplicidad de las reglas de regulación se compensa con el número de parámetros que describen las funciones de membresía. De hecho, si necesita seleccionar tres coeficientes para el controlador PID, en el caso de la lógica difusa, solo una función triangular necesita 3 números para los vértices. Si para cada variable de entrada necesitamos 3 funciones de membresía + 3 para la salida, ¡resulta que necesitamos establecer 3 x 3 x 3 + 3 x 3 = 36 parámetros!
Pero no todo es tan triste. Para una primera aproximación y configuración inicial, todo se puede simplificar.
Habiendo hecho algunas suposiciones para el ajuste inicial del controlador:
- Establecemos la simetría de las funciones con respecto a cero, luego, en lugar de dos números para el máximo y el mínimo, puede especificar uno: Max y, en consecuencia, se definirá como un rango [ -Max ... Max ].
- Establecemos una distribución uniforme de funciones, luego podemos calcular la posición de todos los vértices de los triángulos en función de un rango dado.
- Para tres funciones, las coordenadas de los vértices se definen como –Max, 0, Max.
- Establecemos que la base del triángulo de todas las funciones de membresía es la misma.
Por lo tanto, en lugar de 36 parámetros independientes, deberíamos especificar solo 4, la desviación máxima de 0 para tres variables de entrada y una salida, a saber:
uMax : amplitud de la acción de control
(-uMax ... uMax) ;
deltaMax - desviación máxima
(-deltaMax ... deltaMax) ;
divMax - derivada máxima de desviación
(-divMax ... divMax) ;
div2Max - segunda derivada máxima de la desviación
(-div2Max ... div2Max)En las funciones de faseización e inferencia difusa, utilizamos estas señales para calcular los parámetros teniendo en cuenta los supuestos aceptados.
Configuración del controlador propuesta en el libro por V.V. Gostev “Reguladores difusos en sistemas de modelado automático”, para el caso de la faseización por tres funciones de membresía, se proponen los siguientes parámetros:
uMax = 30 - la amplitud de la acción de control;
deltaMax = 0.01 - desviación máxima;
divMax = 0.07 - derivada máxima de la desviación;
div2Max = 1 es la segunda derivada máxima de la desviación.
Comparación transitoria
En el gráfico de transitorios, la coincidencia de un efecto dado y el resultado obtenido es casi completa:

Figura 11.a Transitoria. Controlador PID
| 
Figura 11.b Transitoria. Lógica difusa
|
Se pueden ver diferencias obvias en los gráficos de la desviación obtenida y la acción de control:

Figura 12.a. Gestión. Controlador PID
| 
Figura 12.b. Gestión. Lógica difusa |
A partir de una comparación de las figuras, se ve que el controlador difuso proporciona menos errores y mejor transitorios.
Comparemos los transitorios en el sistema si establecemos una acción de control gradual. Los resultados en la Figura 13:

Figura 13.a. Efecto de paso. Controlador PID.
| 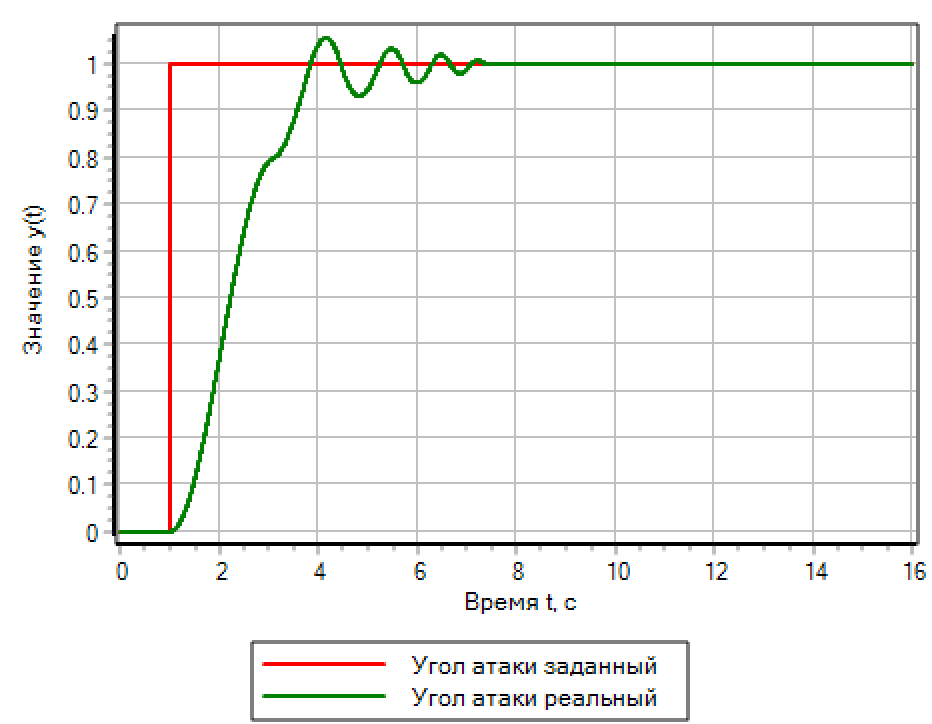
Figura 13.b. Efecto de paso. Lógica difusa. |
Para una acción gradual, un controlador basado en lógica difusa proporciona la mejor calidad transitoria. El controlador PID, que se configura automáticamente en un proceso suave, causa oscilaciones con sobreimpulso que son el doble del paso establecido.
Ajuste del controlador basado en lógica difusa por método de optimización
Intentemos seleccionar los parámetros del controlador difuso mediante el método de optimización, tal como los seleccionamos para el controlador PID. Como criterio, establecemos la desviación estándar menor que 0.001.
Cabe señalar que este método no es del todo correcto, porque para los profesionales está claro qué ángulos y qué velocidades son las máximas y mínimas para cada pieza de concierto, lo que le permite establecer restricciones en los parámetros optimizados de manera más consciente, establecemos los parámetros predeterminados y vemos qué sucede.
El método de optimización con la configuración predeterminada calculó los siguientes valores de los rangos de los parámetros de optimización:
uMax = 19.377 - la amplitud de la acción de control;
deltaMax = 1.095 - desviación máxima;
divMax = 0.01 - derivada máxima de la desviación;
div2Max = 2.497 es la segunda derivada máxima de la desviación.
En el caso de una optimización simple de la desviación, los parámetros obtenidos proporcionan la precisión especificada, sin embargo, esto causa oscilaciones de alta frecuencia de la acción de control.
La función de transición y las acciones de control se presentan en la Figura 14.a
 Figura 14.a. Lógica difusa. Ajuste de desviación. Figura 14.a. Lógica difusa. Ajuste de desviación.
| 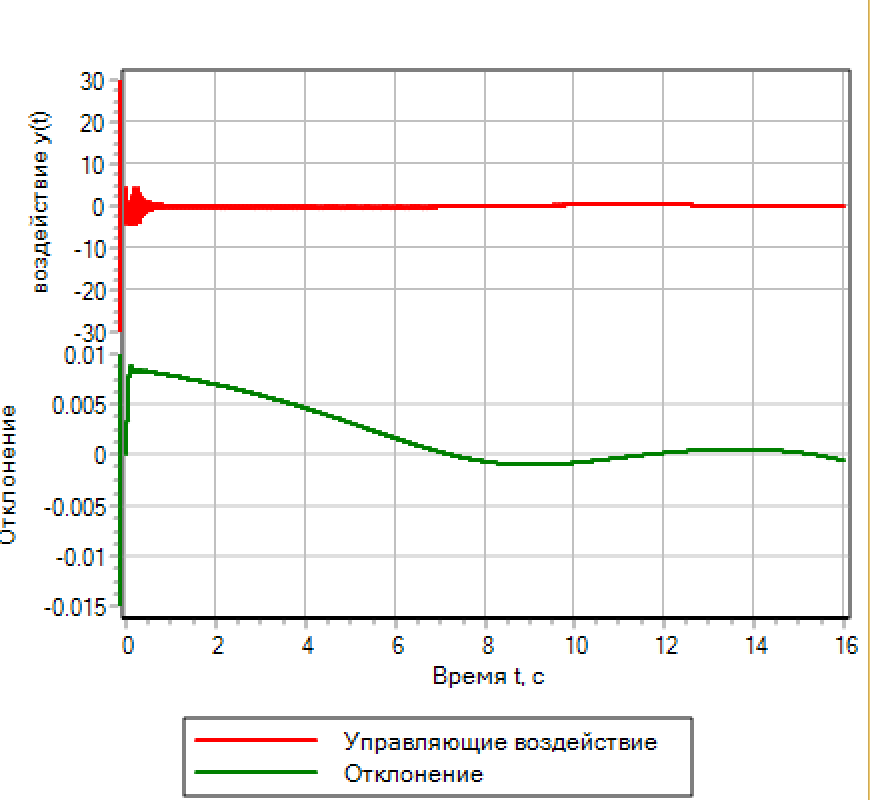 Figura 14.b. Lógica difusa. Establecimiento por desviación y número de respuestas. Figura 14.b. Lógica difusa. Establecimiento por desviación y número de respuestas. |
Para mejorar el proceso transitorio, se puede agregar al criterio de optimización el número de cambios del regulador del valor negativo al positivo del efecto regulador (esquema en la Fig. 15).
 Figura 15. Esquema para la optimización por 2 criterios.
Figura 15. Esquema para la optimización por 2 criterios.El cálculo mediante el método de optimización según dos criterios proporciona los siguientes valores de parámetros:
uMax = 19.714 - la amplitud de la acción de control;
deltaMax = 1.0496 - desviación máxima;
divMax = 0.01 - derivada máxima de la desviación;
div2Max = 1.7931 es la segunda derivada máxima de la desviación.
Se puede ver que cuando se agregó el número de disparos al criterio de optimización, fue posible reducir la frecuencia de conmutación del regulador (ver Fig. 14.b). Por lo tanto, podemos decir que el método de optimización funciona incluso cuando no sabemos nada sobre la física del objeto y simplemente seleccionamos los parámetros numéricos sin pensar en su significado físico.
Creando tu propio controlador basado en lógica difusa
Arriba, creamos el controlador de acuerdo con un esquema ya preparado y bastante simple, todos los términos de variables lingüísticas fueron conectados por el operador lógico I. Dado que tenemos el mismo número de términos en las entradas y salidas, esta es la solución más simple y obvia.
Tratemos de hacer un controlador cuya salida no tenga 3 términos, pero, por ejemplo, 5:
reducir rápidamente, reducir, no cambiar, aumentar, aumentar rápidamente . Y en la entrada lo mismo.
Cambiemos la lógica del regulador, para empezar, simplificando el algoritmo de control tanto como sea posible.Anotamos las reglas:1) Si es más grande y crece t => disminuya rápidamente.2) Si más => disminuye.3) Si la norma => no cambia.4) Si menos => aumenta.5) Si menos y tienen menshaetsya => aumento rápidamente.En este caso, tenemos 5 términos (5 funciones triangulares) para la variable de salida. Aceptamos que se distribuyan uniformemente entre -uMax y + uMax.Suponemos que las funciones triangulares están compuestas de tal manera que cuando las funciones de membresía del término toman valores máximos, las funciones vecinas toman valores cero (ver Fig. 5).Como parámetros para la salida, solo se utilizarán la desviación y la tasa de cambio de la desviación.Para acelerar los cálculos, utilizamos las fases de salida del método por el centro de gravedad de los puntos (ver Fig. 7).El circuito del controlador en este caso se verá como se muestra en la Figura 15.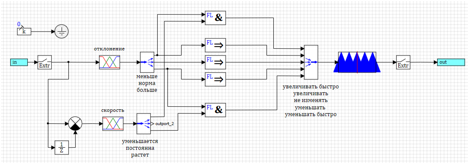 Figura 15. Un controlador simplificado basado en lógica difusa.En lugar del rango de la segunda derivada del optimizador, se tomará el valor para el término "aumento". Un intento de ajustar dicho regulador mediante el método de optimización muestra que el regulador está sintonizado, pero la calidad de la regulación del control del sistema deja mucho que desear.El mejor resultado se muestra en la Figura 16.
Figura 15. Un controlador simplificado basado en lógica difusa.En lugar del rango de la segunda derivada del optimizador, se tomará el valor para el término "aumento". Un intento de ajustar dicho regulador mediante el método de optimización muestra que el regulador está sintonizado, pero la calidad de la regulación del control del sistema deja mucho que desear.El mejor resultado se muestra en la Figura 16.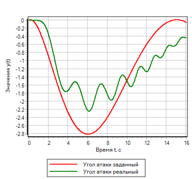 Figura 16. Transitoria para un controlador simplificado.Se puede ver que la regulación se está llevando a cabo, pero no en absoluto como nos gustaría. El hecho es que ejercemos el efecto cuando ya se ha producido una desviación. Intentemos activar la regulación en el momento en que tengamos una desviación en la norma, pero la velocidad muestra que aumentará o disminuirá.1) Si menos y disminuye => aumenta rápidamente.2) Si la norma y aumenta => disminuye.3) Si la norma => no cambia.4) Si la norma y disminuye => aumenta.5) Si es más grande y crece => disminuye rápidamente.
Figura 16. Transitoria para un controlador simplificado.Se puede ver que la regulación se está llevando a cabo, pero no en absoluto como nos gustaría. El hecho es que ejercemos el efecto cuando ya se ha producido una desviación. Intentemos activar la regulación en el momento en que tengamos una desviación en la norma, pero la velocidad muestra que aumentará o disminuirá.1) Si menos y disminuye => aumenta rápidamente.2) Si la norma y aumenta => disminuye.3) Si la norma => no cambia.4) Si la norma y disminuye => aumenta.5) Si es más grande y crece => disminuye rápidamente.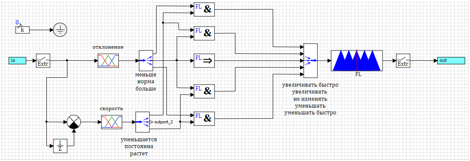 Figura 17. Control por la tasa de cambio de desviación.Los resultados del funcionamiento del controlador sintonizado por el método de optimización se presentan en las Figuras 18a y 18b.
Figura 17. Control por la tasa de cambio de desviación.Los resultados del funcionamiento del controlador sintonizado por el método de optimización se presentan en las Figuras 18a y 18b.
Figura 18.a. El proceso de transición.
| 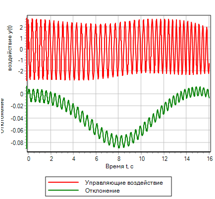
Figura 18.b. Gestión |
El control sobre la tasa de cambio de desviación mejoró significativamente el transitorio. Sin embargo, si observa detenidamente el conjunto de reglas lógicas, vemos que la desviación no está involucrada en la gestión. Si se da un efecto de paso, el controlador de control no generará una acción de control. La figura 19 muestra un ejemplo de un proceso transitorio con una acción de control gradual, se puede ver que el controlador no proporciona una acción de control, aunque la desviación es 1.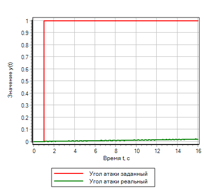
Figura 19.a. El proceso de transición. Paso
| 
Figura 19.b. Gestión. Paso |
Para resolver las desviaciones rápidas, agregamos una acción de control para las desviaciones. Aumentaremos si es menor y disminuiremos si es más. Como ya hay reglas en el conjunto de reglas bajo las cuales reducimos y aumentamos, usamos el operador lógico o:1) Si es menor y disminuye => aumenta rápidamente.2) If ( norma y aumentos ) o más => disminución.3) Si la norma => no cambia.4) Si ( norma y disminuye ) o menos => aumentar.5) simás grande y creciente => disminuye rápidamente.El circuito del controlador de acuerdo con estas reglas se presenta en la Figura 20.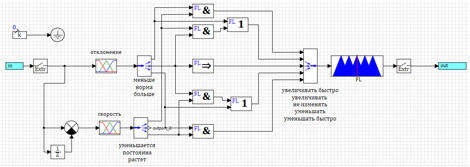 Figura 20. Un controlador con control por desviación y tasa de cambio.Como resultado de la modificación, la calidad del proceso de transición con una acción suave prácticamente no cambió, sin embargo, con una acción gradual, el regulador comenzó a calcular el paso y llevar el ángulo de ataque del cohete al especificado (ver Fig.21).
Figura 20. Un controlador con control por desviación y tasa de cambio.Como resultado de la modificación, la calidad del proceso de transición con una acción suave prácticamente no cambió, sin embargo, con una acción gradual, el regulador comenzó a calcular el paso y llevar el ángulo de ataque del cohete al especificado (ver Fig.21).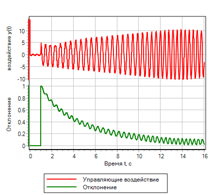
Figura 21.a. El proceso de transición. Paso
| 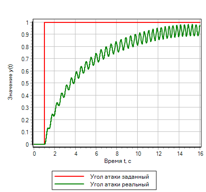
Figura 21.b. Gestión. Paso |
En conclusión, una vez más, "mejoremos" nuestro regulador.Intentemos usar la segunda derivada de la desviación, para comenzar el impacto, antes de que la desviación y su velocidad hayan cambiado. De hecho, con la aplicación de la fuerza, tenemos una aceleración a la que ya podemos responder.Intentemos agregar la segunda derivada a la ley de la regulación en lugar de la primera derivada de la velocidad. Tendremos un efecto regulatorio adicional en el caso en que nuestra segunda derivada muestre que habrá una desviación. Las reglas generales se verán casi iguales, solo entre paréntesis tenemos tres términos, la desviación y la velocidad son normales, y la segunda derivada se desvía:1) Si es menor y disminuye => aumenta rápidamente.2) Si (normal y constante y se acelera ) o más => disminución .3) Si la norma => no cambia.4) Si ( normal y constante y se ralentiza ) o menos => aumenta.5) Si es más grande y crece => disminuye rápidamente .El circuito de este regulador se muestra en la Figura 22. Para ahorrar espacio en el circuito, las expresiones lógicas "y" escritas en las reglas entre paréntesis se calculan en el submodelo marcado con " & ".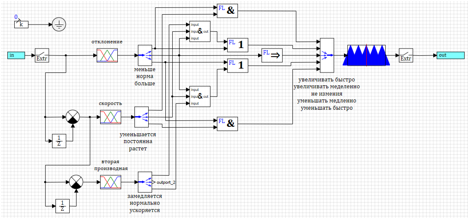 Figura 22. Controlador lógico difuso con control de la segunda derivada.Después de seleccionar los parámetros mediante el método de optimización para la desviación y el número de inclusiones, se obtuvieron los siguientes parámetros:uMax = 27.4983 - la amplitud de la acción de control;deltaMax = 0.0433 - desviación máxima;divMax = 0.0966 - derivada máxima de la desviación;div2Max = 1.0828 - la segunda derivada máxima de la desviación.El proceso transitorio se muestra en la Figura 23. Se puede ver que el regulador resultante tiene el mejor rendimiento de todos los considerados anteriormente, pero para un efecto dado. Las desviaciones y las acciones de control son el mínimo de todo lo considerado en este texto.
Figura 22. Controlador lógico difuso con control de la segunda derivada.Después de seleccionar los parámetros mediante el método de optimización para la desviación y el número de inclusiones, se obtuvieron los siguientes parámetros:uMax = 27.4983 - la amplitud de la acción de control;deltaMax = 0.0433 - desviación máxima;divMax = 0.0966 - derivada máxima de la desviación;div2Max = 1.0828 - la segunda derivada máxima de la desviación.El proceso transitorio se muestra en la Figura 23. Se puede ver que el regulador resultante tiene el mejor rendimiento de todos los considerados anteriormente, pero para un efecto dado. Las desviaciones y las acciones de control son el mínimo de todo lo considerado en este texto.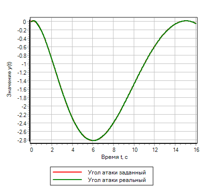
Figura 23.a. El proceso de transición.
| 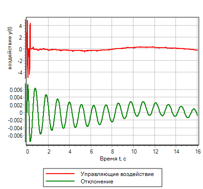
Figura 23.b. Gestión. |
Conclusiones
Un controlador basado en lógica difusa puede proporcionar un transitorio de mayor calidad para el control de cohetes que un controlador PID.El ajuste del controlador basado en la lógica difusa se puede hacer usando herramientas de optimización.Un controlador basado en lógica difusa proporciona una mayor flexibilidad en el ajuste y una mejor calidad transitoria. Pero requiere establecer más parámetros.Descargue el archivo de modelos utilizados en la preparación de este texto, para estudio independiente aquí ...