En este artículo, hablaremos sobre billeteras deterministas, generación de claves jerárquicas y cómo funciona matemáticamente y en qué casos es conveniente ponerlas en práctica. Este material será útil para especialistas cuyas actividades están relacionadas con pasarelas de pago, billeteras Bitcoin y otras tiendas de monedas. Además, el material será de interés para quienes estén interesados en la criptografía elíptica y los esquemas de implementación de claves de firma electrónica.
Billetera determinista
En primer lugar, definamos qué es una billetera determinista. Cuando hablamos de generación de claves, a menudo usamos la palabra "billetera", porque en el contexto de las criptomonedas, poseer una clave privada es una prueba de propiedad de monedas, y en este caso, la billetera y la llave tienen un significado similar.
La billetera determinista es una billetera en la que todas las claves privadas utilizadas se generaron a partir de un secreto compartido por todas las claves. La peculiaridad es que es posible desde un secreto generar cualquier número de pares de claves para la firma electrónica. Puede usar nuevas direcciones para cada pago entrante y cambio.
Convenientemente, las claves de dicha billetera se pueden transferir fácilmente a otro dispositivo, hacer una copia de seguridad y luego restaurarla, porque de hecho solo necesita reservar un secreto principal. Además, todas las claves privadas generadas a partir del secreto principal no están conectadas entre sí. Es imposible rastrear la conexión entre las direcciones generadas (para determinar que todas pertenecen a un usuario), y al tener la clave privada generada, no puede restaurar el secreto compartido.
Codificación secreta básica
Ahora hablemos de codificar el secreto principal. Hay un enfoque estandarizado que se definió en BIP39. Esta es la codificación de codificación de verificación del secreto principal en una frase mnemónica: un conjunto de palabras que es fácil de escribir en papel y, si es necesario, recordar. Al ingresar, es posible verificar la suma de verificación, es decir, identificar un error, si lo hay, con una probabilidad bastante alta.
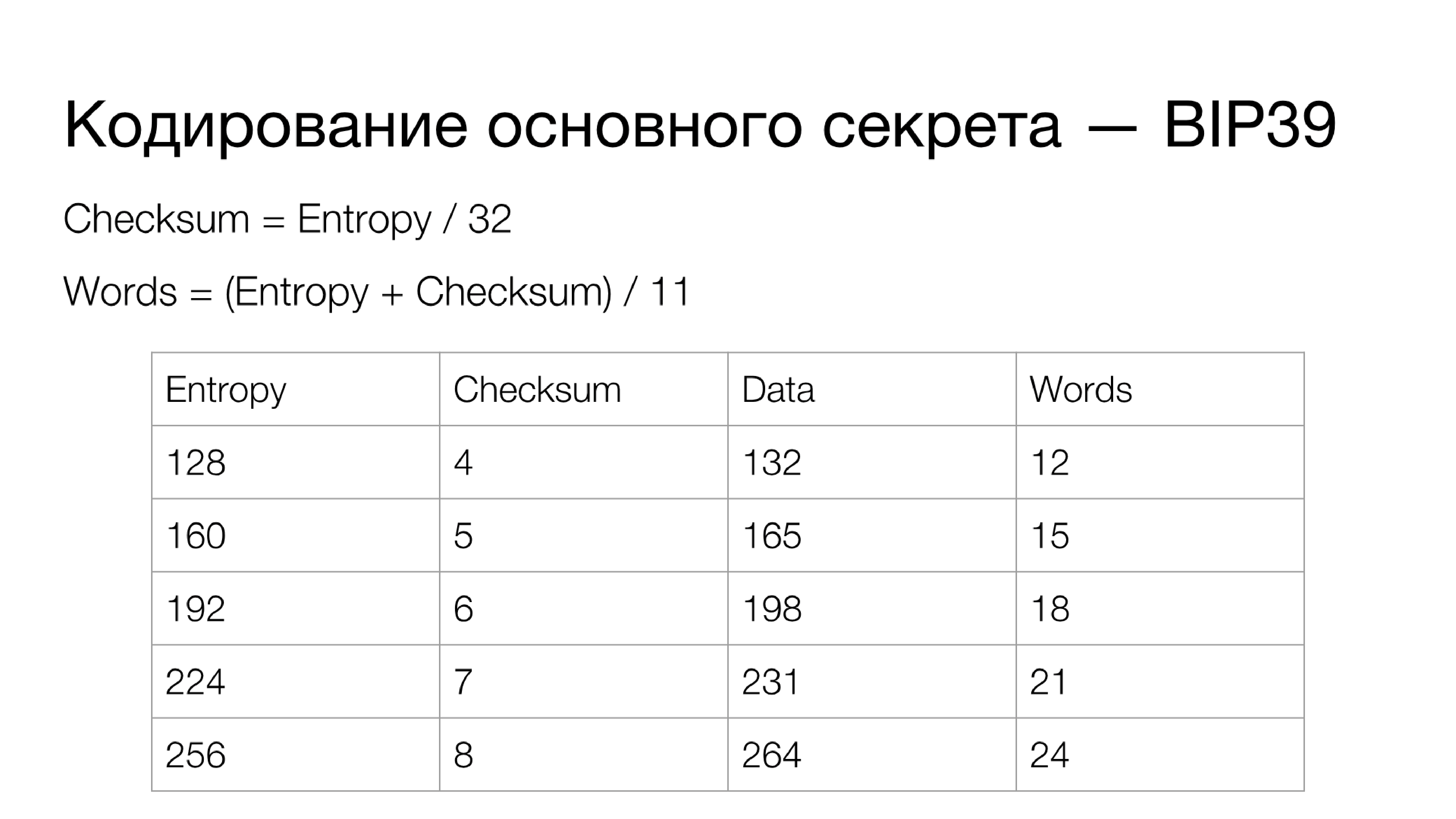
Como funciona De hecho, tiene el secreto principal (Entropía): los datos a partir de los cuales se expanden todas las claves personales de la billetera. Este secreto puede tener diferentes longitudes. En cuanto a la suma de verificación: por cada 32 bits de entropía hay 1 bit de la suma de verificación, es decir, la fórmula calcula la suma de verificación como la longitud de la entropía en bits divididos por 32.
La entropía se concatena con una suma de comprobación, que se calcula como un doble hash SHA-256 (SHA-2 con una longitud de 256 bits), después de lo cual se corta el número requerido de bits. Los datos concatenados se transfieren a otro sistema de números: del sistema binario al sistema de números en la base de 2048 (como puede ver, 2048 es
) Y si agrega la longitud de los bits de entropía y la suma de verificación, obtendrá un múltiplo de 11. Por lo tanto, obtenemos el número de palabras en la frase mnemónica de salida.
De hecho, los datos se "dividen" en partes de 11 bits. Hay un diccionario de 2048 palabras (
) a los que se aplican ciertos requisitos. El idioma predeterminado del diccionario es el inglés, pero se puede usar cualquier persona. Las palabras no deben exceder una cierta longitud (generalmente un límite de hasta 7 caracteres). Todos ellos deben estar codificados en UTF-8 con una cierta normalización de todos los caracteres. Obligatorio es la unicidad de cada palabra en los primeros cuatro caracteres.
Los primeros cuatro caracteres identifican de manera única la palabra en el diccionario, y los caracteres restantes se usan para completar esta palabra en una forma conveniente para leer, memorizar, etc. Por lo tanto, cada pieza de datos que consta de 11 bits recibe una coincidencia inequívoca en la forma de una palabra de diccionario Si la entropía de su secreto es de 256 bits, los datos para la codificación serán de 264 bits y su frase mnemónica contendrá 24 palabras. Este es el enfoque principal para cifrar secretos de billetera en BIP39, que se usa con mayor frecuencia en la práctica.
Para hacer una copia de seguridad en el futuro y usarla, está invitado a escribir esta frase en un medio externo. El papel que guardará en un lugar seguro es lo mejor. Para que pueda restaurar el acceso completo a todas sus claves.
Tipos de carteras deterministas
Las carteras deterministas vienen en dos tipos. Considere sus principales diferencias.
El primero es el más simple. El secreto principal aquí se concatena con el índice de la clave secundaria que queremos obtener, después de lo cual se trituran los datos concatenados. La mayoría de las veces esto sucede usando la función hash SHA-256.
El segundo tipo incluye billeteras deterministas jerárquicas (billeteras HD), cuyos principios se definen en BIP32, y son un enfoque muy común para la generación de claves jerárquicas.
Generación determinista
Considere las diferencias entre estos tipos de billeteras en el diagrama.
Una billetera determinista ordinaria tiene una semilla, a partir de la cual se genera directamente una gran cantidad de claves privadas. Su número solo puede estar limitado por la dimensión del índice, que se concatena con el secreto antes del hash. Por lo general, son 4 bytes, es decir, el espacio de opciones posibles permite alrededor de 4 mil millones de claves de billetera deterministas únicas. En la práctica, esto debería ser suficiente para cualquier situación.
Generación determinista jerárquica
Pasemos a una billetera determinista jerárquica, cuyo esquema de implementación clave se presenta de forma simplificada hasta ahora. Hay semilla, de la cual se obtiene un par de claves maestras directamente. Si en una billetera determinista ordinaria obtenemos una clave privada, entonces aquí obtenemos un par de claves. Además, hay niveles de jerarquía, en cada uno de los cuales calculamos el índice para generar la clave secundaria. También podemos construir ramas de clave pública y ramas de clave privada.
Niveles de jerarquía
Con respecto a las billeteras HD, vale la pena señalar que de acuerdo con las reglas BIP32 en cada nivel de la jerarquía, un nodo de generación tiene tres objetos: una clave privada, una clave pública y un código de cadena que se utiliza para generar el siguiente nivel de jerarquía.
Esquema de generación jerárquica
Consideremos con más detalle el esquema de generación de claves para BIP32.
Todo comienza con semilla, también se llama semilla maestra, a partir de la cual se calcula el nivel cero de la jerarquía: un par de claves maestras y código de cadena.
Se puede generar una gran cantidad de pares de claves con índices específicos a partir de un par de claves maestras. Se está formando un nuevo nivel de jerarquía, que se utiliza para generar cuentas. Supongamos que un usuario tiene semilla y quiere crear varias direcciones que serán diferentes entre sí. Las monedas de estas direcciones no se mezclarán, no se publicarán juntas, y en las transacciones terminadas entre ellas no será posible encontrar una conexión. Estas teclas se usarán completamente por separado una de la otra. En una de las cuentas, el grupo clave se utilizará para el presupuesto de trabajo, en la otra para el presupuesto personal y otra cuenta para la contabilidad negra. Las monedas no se mezclarán entre sí.
El siguiente nivel de jerarquía define diferentes cadenas de generación de claves. Con mayor frecuencia, se utilizan cadenas con los índices 0 y 1. Una cadena con índice 0 generará claves finales para formar una dirección para los pagos entrantes, y una cadena con índice 1 generará billeteras para monedas enviadas por el usuario, es decir, el cambio. Esto es necesario para que la billetera a nivel del programa distinga los pagos enviados desde el exterior del cambio, calcule los cambios en el saldo de cada transacción y compile una lista visual con el historial de todos los pagos. Esto simplifica el desarrollo de la billetera y su uso para pagos diarios.
Código de autenticación de mensaje basado en hash
Ahora pasemos al componente matemático de los procesos jerárquicos de generación de claves. Para empezar, considere el código de autenticación de mensaje basado en hash. Esta es una clase diferente para calcular funciones hash. Se diferencia en que toma dos valores en la entrada, y no uno. El primer valor es la clave privada y el segundo es el mensaje en sí.
K es la clave
m - mensaje
opad, ipad: algunos valores constantes necesarios para generar claves que difieren entre sí en diferentes etapas de hashing.
Como función hash, se utiliza SHA-512.
La peculiaridad es que para usar HMAC, debe poseer una clave secreta para obtener el valor hash correcto del mensaje.
Por lo tanto, para calcular el valor hash de HMAC, el valor de la clave XOR es con el valor constante de ipad, después de lo cual se divide el resultado. Un mensaje se concatena a este valor, después de lo cual la clave XOR se calcula con un valor constante, se concatena con un valor hash y luego se vuelve a aplicar hash. Como resultado, obtenemos 512 bits del valor hash.
Funciones de derivación
Veamos algunas funciones que se utilizan para calcular claves jerárquicas.
En primer lugar, estamos interesados en convertir la semilla maestra en un par de llaves maestras. Después de eso, debe obtener la clave privada secundaria y la clave pública secundaria de la clave primaria personal. En el segundo caso, se usa exactamente la misma función que en el primero, pero se agrega la multiplicación del número por el punto base, por lo tanto, no se considerará por separado. El siguiente paso es obtener el público secundario de la clave primaria pública. Vale la pena señalar que no es posible obtener un elemento personal secundario de la clave pública principal. Esta limitación se debe a ciertas propiedades inherentes a las billeteras HD, que consideraremos más a fondo.
Entonces, repasemos cada una de las funciones de generación por separado.
Para obtener la clave maestra del sid maestro, se utiliza la función HMAC, donde la cadena constante "semilla de Bitcoin" se transmite como la clave, y los datos secretos principales en sí como un mensaje. Por lo tanto, se obtiene un valor hash de 512 bits, que consideramos como dos partes: izquierda y derecha. El lado izquierdo es la clave privada maestra, y el lado derecho será el código de cadena. Además, estos valores se utilizarán para generar niveles posteriores de claves secundarias.
Para obtener un maestro público, simplemente multiplique el valor del punto base por el valor de la clave privada maestra. Como puede ver, esto sucede por analogía con las teclas ordinarias en un grupo de puntos en una curva elíptica.
Ahora veamos cómo la clave privada secundaria proviene de la clave privada primaria.
Usaremos la función HMAC nuevamente. Como clave, pasamos el código de cadena del nivel de jerarquía actual, y como mensaje, concatenación, donde la primera parte será la clave principal personal multiplicada por el punto base. De hecho, este es un reparto a un punto y la serialización de este punto. La concatenación se produce con el índice de la clave secundaria que queremos recibir, serializado en 32 bits, es decir, 4 bytes.
Según el resultado de la función HMAC, obtenemos el valor I, y nuevamente lo consideramos por separado: las partes izquierda y derecha de los valores de salida son 256 bits. Entonces la clave privada del niño
calculamos agregando al valor de salida izquierdo
valores de la clave privada principal. La adición se realiza módulo n, donde n es el orden del punto base de la curva elíptica, para no exceder el valor máximo de la clave privada. Por lo tanto, recibimos una clave privada secundaria.
En consecuencia, el código de la cadena secundaria será igual al valor de salida correcto de la función HMAC, es decir
. Si queremos encontrar la clave pública secundaria a partir de la clave primaria personal, multiplicamos el valor
por el valor del punto base en la curva elíptica. Entonces obtenemos la clave pública
.
¿Cómo calculamos la clave pública secundaria a partir de la clave primaria pública?
Aquí el cálculo será un poco diferente. Pasamos la jerarquía de cadena del nivel de jerarquía actual como una clave en la función HMAC, después de lo cual serializamos la clave pública principal y la concatenamos con el índice deseado serializado a 32 bits. Los datos de entrada se obtienen exactamente de la misma manera que en el caso anterior. Para calcular la clave pública, tomamos el lado izquierdo del valor de salida de la función HMAC y lo consideramos como 256 bits tomados módulo del orden del punto base, lo llevamos a un punto en la curva elíptica, es decir, lo multiplicamos por el punto base y luego agregamos el resultado con la clave pública principal . El resultado de la adición también será un punto, y será una clave secundaria pública. El código de cadena para esta clave será el lado derecho del valor de salida de la función HMAC.
Claves coincidentes entre sí
Esto puede plantear una pregunta lógica sobre cómo las claves privadas y públicas obtenidas de diferentes maneras se corresponderán entre sí. ¿Es realmente posible obtener exactamente el mismo valor de una clave pública generada por una vía pública tomando una clave privada obtenida de otra manera y multiplicándola por un punto base? Esto es fácil de verificar.
Si recordamos cómo calculamos la clave secundaria personal y la multiplicamos por el punto base, es decir, la llevamos a la función de punto, y luego recordamos el cálculo de la clave pública secundaria y comparamos estos cálculos, veremos que si consideramos la clave pública primaria como un producto de la clave personal clave del punto base, luego veremos que se realizaron los mismos cálculos, solo en un orden diferente.
En un caso, agregamos las claves privadas y las multiplicamos por el punto base, y en el segundo caso, primero multiplicamos los valores por el punto base, luego los agregamos y obtuvimos el resultado. Basado en el hecho de que la operación de sumar puntos en una curva elíptica es aditiva, podemos decir que estos dos valores son iguales: obtendremos la misma clave pública calculada de dos maneras.
Ejemplo de clave pública
En aras del interés, podemos ver un ejemplo de una clave pública que se obtuvo para los valores de prueba y los cálculos BIP32. Si nuestra entropía consistía en 128 bits, en el sistema de números hexadecimales se verá como la imagen de abajo.
El mismo valor codificado en la frase mnemónica BIP39 se verá como las 12 palabras que se muestran. Si utiliza esta frase mnemónica como semilla maestra para la generación de claves jerárquicas, obtendrá dicha clave privada maestra con el código de cadena de 256 bits correspondiente.
Llaves extendidas
También existen conceptos como clave pública extendida y clave privada extendida. Como se usa Para comprender mejor, describimos la situación visual.
Digamos que tenemos un usuario específico y algún servicio. Un servicio transfiere pagos, por ejemplo en bitcoins, a un usuario con cierta frecuencia. Tanto el usuario como el servicio están interesados en utilizar una nueva dirección para cada pago, a fin de dificultar que un observador externo establezca un hecho y confunda el historial de interacción entre ellos.
En el caso más simple, se vería así: el usuario para cada pago entrante genera un nuevo par de claves, calcula la dirección que pasa al servicio, después de lo cual el servicio puede generar una transacción y realizar el pago. Sin embargo, esto es inconveniente para cualquiera de las partes si la intensidad de estos pagos es alta.
Clave pública extendida
En una situación similar, la clave pública extendida (xPubKey) ayuda a eliminar las molestias. El usuario puede habilitar un servicio de terceros para generar direcciones en lugar de sí mismas que serán conocidas por el servicio, pero solo el usuario tendrá claves privadas. El servicio puede generar cualquier número de direcciones sin el conocimiento del usuario y enviarles fondos, y el usuario puede, a su conveniencia, implementar claves privadas y obtener acceso a cualquiera de estas direcciones.
Como funciona El usuario necesita generar una nueva cuenta en el segundo nivel de la jerarquía de claves, calcular para él la clave pública y el código de cadena para el nivel actual. Después de eso, debe transferir la clave pública y el código de cadena al servicio. Por conveniencia, se introdujo la codificación Base58Check, de la que hablamos (aquí hay una versión especial). A continuación, la clave pública, el código de cadena y la suma de verificación se concatenan. Todo esto está codificado en el sistema de números base 58 y obtenemos una clave pública extendida ya codificada de acuerdo con cierto estándar. Comienza con los caracteres "xpub", que se reconoce fácilmente. Se verá como se muestra en la imagen.
Un servicio puede aceptar dicha clave e implementar claves públicas para el usuario a través de BIP32, recibir direcciones de ellas y pagarlas. Sin embargo, solo el usuario puede calcular las claves privadas correspondientes.
Derivación endurecida
En la generación jerárquica de claves existe una derivación reforzada. Este es un enfoque que no permite el cálculo de claves públicas secundarias a partir de la clave pública principal correspondiente. Esto difiere de la generación normal en que en él usamos la concatenación del punto serializado como la clave pública principal como un mensaje para la función HMAC, y en la derivación reforzada usamos la serialización de la clave privada principal.
Además, el cálculo del índice es diferente. El índice en la generación normal se serializa directamente a 32 bits, y en la derivación reforzada se convierte ligeramente: se le agrega un valor constante
eso establece el bit más significativo en 1 (se hace fácil distinguir entre los tipos de derivación). En consecuencia, el espacio de variantes de posibles claves es el mismo para la generación normal y la derivación endurecida, y es igual a
.
Por lo tanto, al tener una clave pública principal y una derivación reforzada, no es posible calcular las claves públicas secundarias. Si el atacante recibe la clave pública principal, no podrá calcular las claves secundarias. Por lo tanto, no podrá calcular las direcciones y su relación con la clave principal recibida. En el caso de la derivación normal, es decir, en la forma habitual, dicha función se puede utilizar y rastrear la relación de direcciones entre ellos.Caminos de generacion
Hablemos sobre las formas en que se pueden generar claves.
En cada nivel de la jerarquía, hay un índice específico que define aspectos de la generación de claves. La ruta de la clave maestra a la clave final se puede escribir mediante barras inclinadas como índices. Si estamos hablando de una clave privada, entonces la grabación comienza con una pequeña "m", y si estamos hablando de generar una clave pública, entonces con una "M" grande. Si el índice está indicado por un apóstrofe, entonces debe entenderse que estamos hablando de derivación endurecida, sin un apóstrofe - derivación normal.Considere una de las rutas populares de generación de claves utilizadas en BIP32, donde se definieron las claves jerárquicas.
Utiliza una ruta donde la clave maestra es el nivel cero de la jerarquía. Los siguientes son los índices de cuentas que designan al mismo usuario, seguidos por cadenas donde puede haber cadenas de direcciones que se publican afuera para aceptar pagos entrantes, y con el índice 1, se crearán esas cadenas a las que el usuario se envía los pagos a sí mismo (más a menudo todo esto es rendición). El índice final se utilizará para generar las claves a partir de las cuales se calcularán las direcciones.Para calcular la primera clave con índice 0 de acuerdo con el estándar BIP32, tendremos m, 0 con la generación de endurecido, cadena - 0, índice - 0 (m / 0 '/ 0/0). Entonces obtenemos la ruta para la primera clave generada jerárquicamente.Hay una sugerencia para mejorar Bitcoin, se llama BIP43, que implica escribir en el primer nivel de la jerarquía el número de mejora, que ofrece una nueva ruta de generación (m / bip_number '/ *).
Por lo tanto, apareció BIP44, que usó la característica de la oración anterior, es decir, el índice 44 está escrito para el primer nivel de jerarquía, y propuso las siguientes mejoras: en el índice del segundo nivel de jerarquía, registre un cierto valor que corresponderá al tipo de moneda que usamos para esta billetera. Ahora, las claves para diferentes monedas se pueden implementar y usar en una billetera.
Para Bitcoin, la ruta se verá como “m / 44 '/ 0' / 0 '/ 0/0”, para Bitcoin testnet - “m / 44' / 1 '/ 0' / 0/0”, para Litecoin - “m / 44 '/ 2' / 0 '/ 0/0 ”, para Dash -“ m / 44' / 5 '/ 0' / 0/0 ”. Curiosamente, Ethereum usa exactamente la misma curva elíptica para calcular claves y firmar digitalmente y para su billetera la ruta se verá como "m / 44 '/ 60' / 0 '/ 0/0".Hay otra mejora: BIP45. La mejora está dirigida a determinar las reglas para generar claves en caso de su uso en billeteras de múltiples firmas y la formación de direcciones usando BIP16, es decir, P2SH. Incluye la oración BIP43 e indica el índice 45 en el primer nivel de la jerarquía; en el segundo nivel de la jerarquía, requiere una indicación de un firmante (cosignatario).
Por ejemplo, hay una regla de firma múltiple 3 de 5. Por lo tanto, hay 5 signatarios, pero para gastar monedas, necesita al menos 3 firmas. Por lo tanto, cada uno de los firmantes tendrá una billetera HD con su propia semilla maestra e indicará su número de serie en su camino. Se puede calcular como un índice al ordenar las claves generadas en el primer nivel de la jerarquía de cada usuario. Supongamos que, en el primer nivel, cada usuario genera claves, intercambian entre sí, clasifican y descubren quién tiene qué índice para el segundo nivel de la jerarquía. Esto es necesario para eliminar aún más la necesidad de interactuar de esta manera, e inmediatamente generar direcciones correctamente y conocer su número de serie.Es decir, puede intercambiar la clave pública extendida una vez para poder, independientemente, independientemente de otros miembros del grupo, formar direcciones de múltiples firmas y aceptar pagos en ellas.Preguntas
Pasemos a las preguntas frecuentes.- ¿Cómo difieren las semillas maestras en diferentes monedas?La semilla es un número generado aleatoriamente, alguna secuencia de bits, o es una frase mnemónica generada, por ejemplo, de acuerdo con BIP39, que se utiliza para generar claves. Se puede usar tanto para una moneda como para cualquier otra; no es necesario usar diferentes frases mnemotécnicas para diferentes monedas. Además, existe BIP44, que define las reglas para generar claves para diferentes monedas a partir de la misma frase mnemónica. Estas claves privadas no se cruzarán entre sí, sino que se utilizarán para diferentes direcciones de diferentes monedas.- Diccionario de BIP39, donde se estandarizan 2048 palabras para una frase mnemónica? ¿Puedo usarlo en todas las billeteras y aplicaciones?El hecho es que este estándar se describe para BIP39. Es para BIP39 que hay diccionarios: inglés, dos japoneses, chinos, italianos, rusos, ucranianos, etc. Es decir, si alguna aplicación afirma que usa BIP39 y permite importar y exportar una frase mnemónica, significa que también usa un conjunto de palabras lo mismo Sin embargo, hay billeteras que no usan BIP39, sino su propia modificación. Debe mirar la descripción de la billetera y usar el desarrollo estandarizado o su propio desarrollo o el desarrollo del servicio que ofrece la billetera.- En los intercambios y almacenes centralizados como Coinbase, ¿las claves de billetera para todos los usuarios se generan a partir de la misma frase común para todos o no?Es difícil de decir, porque no abren su estructura interna, pero los nuevos servicios que aparecen pueden generar claves por separado, o usar el estándar BIP32, o usar su versión modificada. Esos servicios que existían antes de que aparecieran los estándares para la generación de claves jerárquicas, muy probablemente, continúan generando claves privadas separadas. Quizás es así como son más fáciles de administrar si hay una gran rotación de todas las claves."¿Es la clave un punto en la curva elíptica, es decir, dos números muy grandes X e Y?"La clave pública: sí, este es un punto en la curva elíptica, y la clave privada es un número natural que muestra cuántas veces debe agregarse el punto base. La clave pública en sí consta de dos valores: estas son las coordenadas X e Y, cada una de las cuales tiene un tamaño de 256 bits.- ¿Qué es "lanzar a punto" y la serialización de punto e índice?La reducción a un punto significa que hay un número natural, que consideramos como una clave privada. Agregamos el punto base con nosotros tantas veces, es decir, en el grupo de puntos en la curva elíptica, solo se define la operación de suma, luego podemos multiplicar el punto por un número natural. La serialización de un punto significa registrar de cierta manera dos coordenadas. Esto puede ser un registro comprimido, pero no es necesario. Comprimido en el sentido de que una de las coordenadas, a saber, Y se convierte en un signo, luego los datos se sustituyen en la ecuación y observa dónde está el punto: arriba o abajo. En el caso de la serialización de índice, debe comprender que un número regular, que, según el tamaño, se puede escribir en bytes o bits. Cuanto mayor sea el número, se necesitarán más datos. En el caso de los cálculos que examinamos,se requiere un número de cierta longitud. Debe serializarlo a una longitud específica: 4 bytes. Como resultado, esto se refiere a convertir el índice a un número de 4 bytes. Si los valores superiores permanecen vacíos allí, serán cero.- ¿A quién se le ocurrieron estos cálculos para las funciones de derivación de las billeteras HD? ¿Por qué tales fórmulas donde hay justificaciones y donde puedes leer más sobre esto?Puede leer con mayor precisión en BIP32, si está interesado en una frase mnemónica, luego en BIP39, etc. Puede abrir GitHub y encontrar un usuario con el apodo de Bitcoin. Tiene un repositorio de Bitcoin donde se almacena el código fuente de Bitcoin, y tiene un repositorio de BIP (fuente primaria), donde se registran todas las sugerencias para mejorar Bitcoin.Se les ocurrió la idea de hacer cálculos de esta manera, porque está vinculada a un grupo de puntos de una curva elíptica. Cuando deseaba lograr una funcionalidad que le permitiera calcular por separado las ramas de las claves públicas y privadas, manteniendo su correspondencia entre ellas, esta fue la opción de implementación más fácil. De hecho, los desarrolladores utilizaron la opción más simple, que le permite obtener propiedades interesantes utilizando la criptografía que ha sido probada por el tiempo. Los autores de las mejoras propuestas son muchos. La comunidad de Bitcoin, cuyos participantes ofrecen algún tipo de desarrollo de mejoras y transformaciones matemáticas, es bastante grande.- ¿La derivación endurecida siempre está solo en el segundo nivel de la jerarquía?Todo depende de la situación. En el caso de generar claves para la firma múltiple, tiene sentido hacer una derivación reforzada solo en el primer nivel de la jerarquía. En BIP44, la derivación endurecida se aplica a los primeros tres niveles: en el primer nivel está el número del BIP en sí, en el segundo está el número de cuenta donde es relevante, en el tercero está el número de moneda, donde también tiene sentido. Suponga que es poco probable que le guste si publica la clave pública, y a través de ella las personas pueden rastrear todas sus direcciones en Bitcoin. Si usa una cuenta para recibir pagos de ciertos servicios, puede revelar esta clave y no necesita derivación reforzada aquí.- ¿Dónde es posible aplicar la generación de claves jerárquicas?Puede aplicarlo cuando trabaje con el intercambio para que el intercambio siempre le pague a diferentes direcciones. Aunque en este caso es mejor organizar todo esto manualmente. Esto es más relevante para las billeteras digitales cotidianas, porque aquí es un proceso muy simple crear una copia de seguridad de claves privadas y restaurar una billetera. También se admite la generación de claves para diferentes monedas, y el estándar en sí ya se usa en diferentes implementaciones de billeteras digitales. Las claves entre estas billeteras son convenientes para transferir usando la misma frase mnemónica.Este tema se trata en una de las conferencias del curso en línea de blockchain " Generación de claves jerárquicas ".