Introduccion
Para determinar las características balístico-temporales del movimiento del centro de masa del paracaidista, uno tiene que elegir un modelo matemático simplificado que sea bastante accesible para la investigación analítica y al mismo tiempo conserve los rasgos más característicos del objeto original.
Para construir modelos matemáticos simplificados del movimiento del paracaidista, se lleva a cabo un análisis, determinación, sistematización de parámetros constantes y de tiempo.
Actualmente no existen métodos regulares y suficientemente justificados para construir modelos matemáticos no lineales, sin embargo, para resolver problemas particulares, con la composición correcta de los sistemas iniciales de ecuaciones diferenciales no lineales, los métodos numéricos para resolverlos pueden dar resultados bastante adecuados.
El propósito de esta publicación es compilar y resolver numéricamente sistemas de ecuaciones diferenciales que describen todas las etapas del movimiento de un paracaidista que aterriza desde un avión, teniendo en cuenta el efecto de los cambios en la altitud y la temperatura de la densidad de masa del aire.
Características balístico-temporales del movimiento de un paracaidista.
Los parámetros variables constantes y limitados incluyen:
H - la altura de la liberación del paracaidista;
V0 - velocidad de la aeronave;
k - peso, altura del paracaidista;
g es la aceleración de la gravedad;
ρ es la densidad del aire;
T es la temperatura del aire.
Los parámetros temporales (variables) incluyen:
tn - tiempo de aterrizaje,
w es la velocidad del viento;
V es la velocidad del paracaidista;
u es la velocidad de los flujos ascendentes (descendentes);
d - deriva (distancia desde la proyección al suelo del punto de expulsión al punto de toma de contacto);
C es el coeficiente de arrastre del objeto de aterrizaje;
F - sección media del objeto de aterrizaje.
Etapas de salto
La primera etapa es una caída libre después de la separación del avión:
 La segunda etapa
La segunda etapa es una disminución en un paracaídas estabilizador:

La propiedad principal del paracaídas estabilizador es la estabilización del paracaidista en la posición más conveniente para el paracaídas principal.
La tercera etapa : llenar la cúpula del paracaídas principal:
 La cuarta etapa
La cuarta etapa es una disminución en el paracaídas abierto:

Compilación de un sistema de ecuaciones diferenciales para todas las etapas de un salto en paracaídas
Elegimos un sistema de coordenadas fijo OXY centrado en el punto de expulsión O. El eje OX coincide con la dirección del componente horizontal de la velocidad del avión. El eje OY se dirige verticalmente hacia arriba en la dirección opuesta a la velocidad vertical del paracaidista.
Asumiremos que el movimiento del paracaidista es plano y ocurre en el plano OXY. Este modelo de un salto puede considerarse como un modelo de un salto en clima tranquilo sin tener en cuenta la influencia del viento.
Creemos que, además del peso, el paracaidista se ve afectado por la fuerza de la resistencia del aire proporcional al cuadrado de la velocidad del paracaidista:
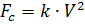
,
donde:
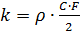
,
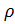
- densidad del aire, C - coeficiente de arrastre, F - sección media del cuerpo.
Con el aumento de la altura, la temperatura del aire cambia:

La temperatura mínima ya se alcanza a una altitud de 10 km. y es -55 ° C. La densidad del aire también depende de la presión. Por lo tanto, al calcular la balística de un salto en paracaídas, es conveniente utilizar la siguiente fórmula para determinar la densidad del aire [1]:
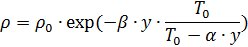
,
donde
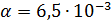
K / m;
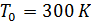
- temperatura al nivel del mar; y es la altura en m;

- densidad del aire en y = 0;
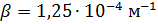
.
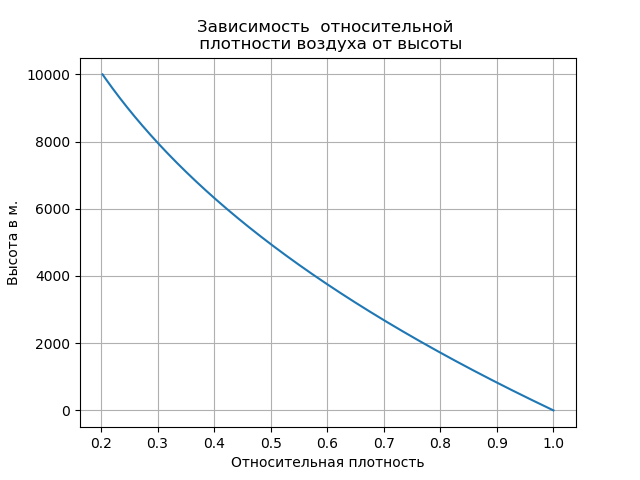
En la práctica de los cálculos, el cuadrado de crecimiento se toma como la sección media; el valor de C se encuentra en la tabla [2]:

Θ denota el ángulo de inclinación de la trayectoria. Bajo los supuestos hechos para los componentes
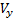
,
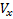
vectores de velocidad V tenemos:

Dividiendo por m los lados izquierdo y derecho de las ecuaciones del sistema resultante y denotando

a través de r, obtenemos:
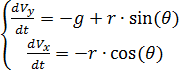
(1)
Anotamos las ecuaciones de movimiento de un paracaidista en forma de un sistema de ecuaciones diferenciales para las funciones V, θ, y (t), x (t).
Dado que:
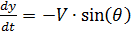
,
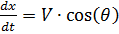
,
y relación de tiempo de diferenciación:

, teniendo en cuenta el sistema de ecuaciones (1) obtenemos:
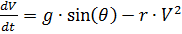
,
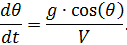
.
Por lo tanto, bajo las condiciones iniciales:
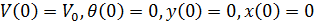
Tenemos el siguiente sistema de ecuaciones diferenciales:
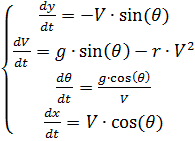
Solución numérica de un sistema de ecuaciones diferenciales (2) usando Python
Para resolver (2), lo reescribimos de la siguiente forma, introduciendo fuerzas de arrastre estabilizadoras controladas por el tiempo y la densidad del aire.
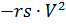
y principal
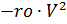
paracaídas, respectivamente, multiplicados por las funciones de control de tiempo ks (t) y ko (t):
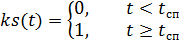
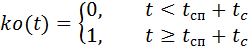
,
donde:
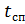
–– tiempo de caída libre del paracaidista;

- el tiempo de funcionamiento del paracaídas de estabilización hasta la apertura del principal.
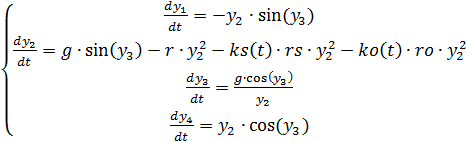
(3)
Listado completo del programa ajustado por cambios en la densidad del aire Obtenemos:
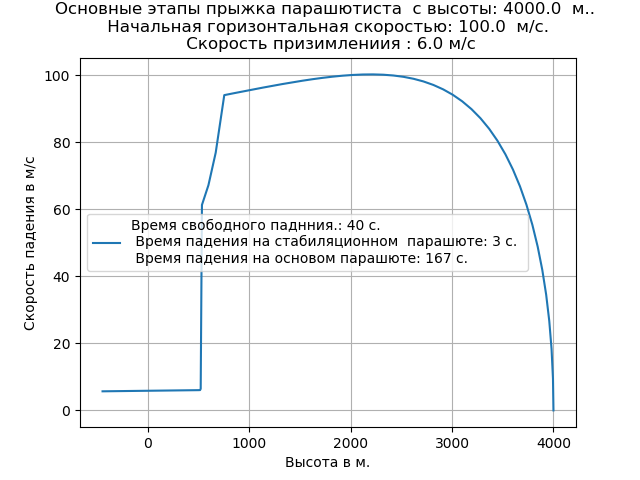
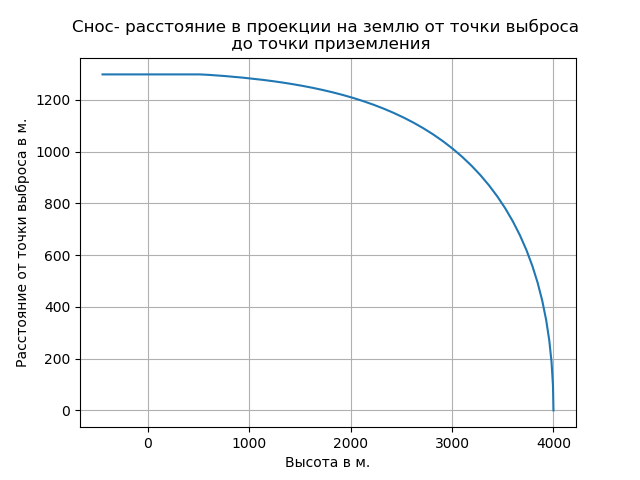
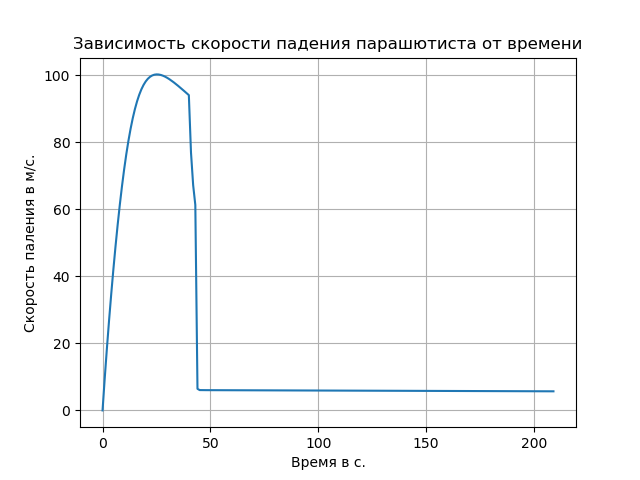
Tener en cuenta el aire enrarecido condujo a un aumento en la tasa de caída libre y cambió la naturaleza de la trayectoria en esta sección.
Este problema se puede resolver con la ayuda de un sistema de dos ecuaciones diferenciales, que se dan a continuación (excluyendo paracaídas y cambios en la densidad del aire):
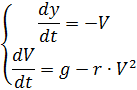
El cambio en las fuerzas de resistencia y la densidad del aire se muestra en la lista debajo del alerón, teniendo en cuenta lo anterior y sin explicación.# - * - codificación: utf8 - * -
de importación numpy *
de scipy.integrate import odeint
importar matplotlib.pyplot como plt
m = 100
r0 = 1.3
c1 = 0.3
c2 = 0.6
c3 = 0.5
c4 = 0.75
S = 70
s = 0.8
ss = 1.5
g = 9.8
cucharadita = 6
tsbp = 10
tp = 90.0
h = 1000.0
beta = 1.25 * 10 ** - 4
alfa = 6.5 * 10 ** - 3
T0 = 300
def ks (t):
si t <tsp:
z = 0
más:
z = 1
volver z
def ko (t):
si t <tsp + tsbp:
z = 0
más:
z = 1
volver z
# dy1 / dt = y2
# dy2 / dt = g- (k1 * y2 ** 2) / m- (k2 * y2) / m- (ks (t) * k3 * y2 ** 2) / m- (ko (t) * k4 * y2 ** 2) / m
def f (y, t):
y1, y2 = y
r = r0 * exp (-beta * y1 * T0 / (T0-alfa * y1))
k1 = 0.5 * r * c1 * s
k2 = 0.5 * r * c2 * s
k3 = 0.5 * r * c3 * ss
k4 = 0.5 * r * c4 * S
retorno [-y2, g- (k1 * y2 ** 2) / m- (k2 * y2) / m- (ks (t) * k3 * y2 ** 2) / m- (ko (t) * k4 * y2 ** 2) / m]
t = rango (0.0, tp)
y0 = [h, 0.0]
[y1, y2] = odeint (f, y0, t, full_output = False) .T
plt.title ("Paracaidismo de 1000 y 800 metros")
plt.plot (y1, y2, label = 'Altitud 1000 m')
h = 800.0
cucharadita = 6
tsbp = 2
tp = 80.0
def ks (t):
si t <tsp:
z = 0
más:
z = 1
volver z
def ko (t):
si t <tsp + tsbp:
z = 0
más:
z = 1
volver z
def f (y, t):
y1, y2 = y
r = r0 * exp (-beta * y1 * T0 / (T0-alfa * y1))
k1 = 0.5 * r * c1 * s
k2 = 0.5 * r * c2 * s
k3 = 0.5 * r * c3 * ss
k4 = 0.5 * r * c4 * S
retorno [-y2, g- (k1 * y2 ** 2) / m- (k2 * y2) / m- (ks (t) * k3 * y2 ** 2) / m- (ko (t) * k4 * y2 ** 2) / m]
t = rango (0.0, tp)
y0 = [h, 0.0]
[y1, y2] = odeint (f, y0, t, full_output = False) .T
plt.plot (y1, y2, label = 'Altura 800 m')
plt.xlabel ('Altura en m.')
plt.ylabel ('Velocidad de combustión en m / s.')
plt.legend (loc = 'mejor')
plt.grid (verdadero)
plt.show ()
Obtenemos:

Conclusión
Se determinan las características balístico-temporales del movimiento del centro de masa de un paracaidista que aterriza desde un avión.
Referencias
- Presión atmosférica
- Gerasimenko I.A. Entrenamiento aéreo: libro de texto. M .: Military Publishing, 1986. Parte 1, p. 32.