Reducción de red neuronal mediante optimización variacional

Hola Habr Hoy me gustaría desarrollar el tema de la optimización variacional y decir cómo aplicarlo a la tarea de recortar canales no informativos en redes neuronales (poda). Al usarlo, uno puede aumentar relativamente fácilmente la "velocidad de disparo" de una red neuronal sin palear su arquitectura.


La idea de reducir elementos redundantes en los algoritmos de aprendizaje automático no es nada nueva. De hecho, es más antiguo que el concepto de aprendizaje profundo: fue antes que las ramas de los árboles decisivos fueron cortadas, y ahora pesan en una red neuronal.

La idea básica es simple: encontramos en la red un subconjunto de pesos inútiles y los ponemos a cero. Sin una búsqueda exhaustiva, es difícil decir qué pesos realmente participan en la predicción y cuáles solo pretenden, pero esto no es obligatorio. Varios métodos de regularización, daño cerebral óptimo y otros algoritmos funcionan bien. ¿Por qué eliminar cualquier peso? Resulta que esto mejora la capacidad de generalización de la red: como regla, los pesos insignificantes simplemente introducen ruido en la predicción o se agudizan especialmente para detectar signos de un conjunto de datos de entrenamiento (es decir, un artefacto de reentrenamiento). En este sentido, la reducción de las conexiones se puede comparar con el método de desconectar neuronas aleatorias (abandono) durante el entrenamiento de la red. Además, si la red tiene muchos ceros, ocupa menos espacio en el archivo y puede leer más rápido en algunas arquitecturas.

Suena bien, pero es mucho más interesante tirar no pesos separados, sino neuronas de capas o canales completamente conectados de los paquetes completos. En este caso, el efecto de la compresión de la red y la aceleración de las predicciones se observa mucho más claramente. Pero esto es más complicado que destruir pesos individuales: si intenta llevar a cabo el daño cerebral óptimo, tomando todo el paquete en lugar de una conexión, es probable que los resultados no sean muy impresionantes. Para poder eliminar sin dolor una neurona, es necesario hacerlo de modo que no tenga una única conexión útil. Para hacer esto, necesita inducir de alguna manera a las neuronas "fuertes" a fortalecerse, y a las "débiles" a debilitarse. Esta tarea ya nos es familiar: de hecho, forzamos a la red a inducir la escasez con algunas restricciones en la agrupación de pesos.

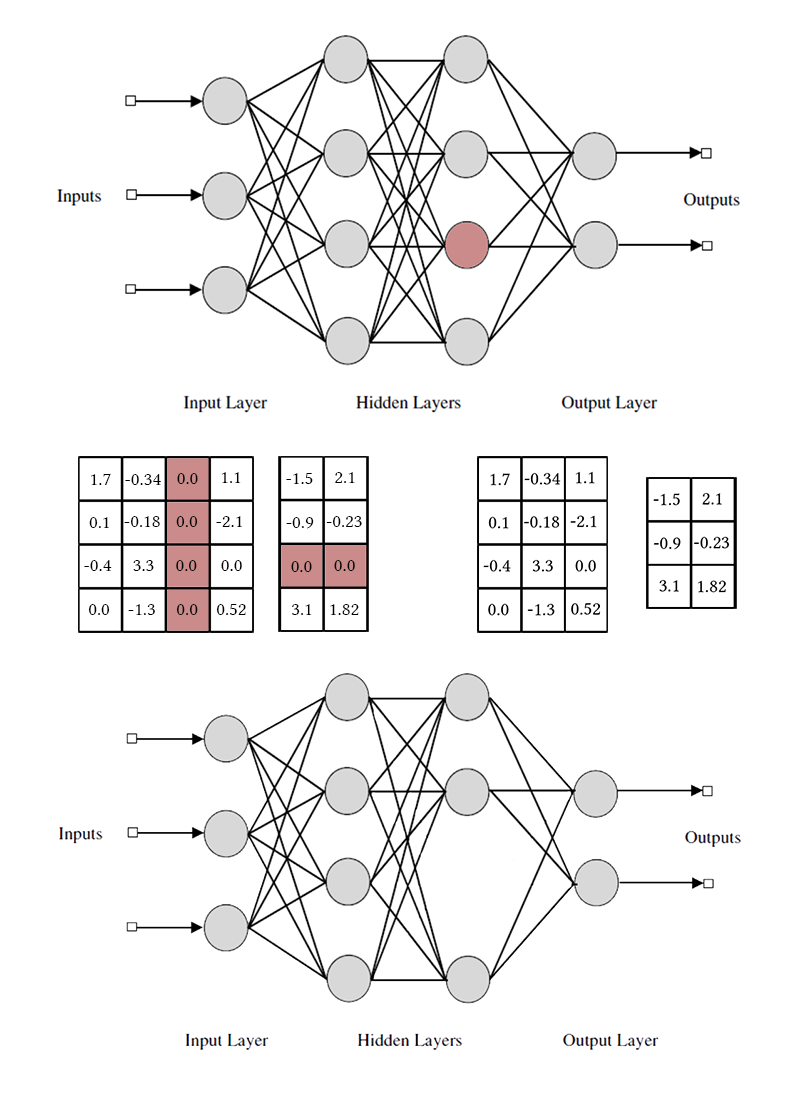
Tenga en cuenta que para eliminar una neurona o un canal convolucional, debe modificar dos matrices de pesos. No distinguiré entre canales convolucionales y neuronas: el trabajo con ellos es el mismo, solo difieren los pesos específicos eliminados y el método de transposición.

La manera fácil: regularización de grupo L1

Para comenzar, le contaré la forma más simple y efectiva de eliminar neuronas adicionales de la red: la regularización grupal de LASSO. La mayoría de las veces se usa para mantener pesos inútiles en redes cercanas a cero; trivialmente se generaliza al caso de canal por caso. A diferencia de la regularización regular, no regularizamos el peso o la activación de la capa directamente, la idea es un poco más complicada. [Poda de canales para acelerar redes neuronales muy profundas; Yihui He y col; 2017]

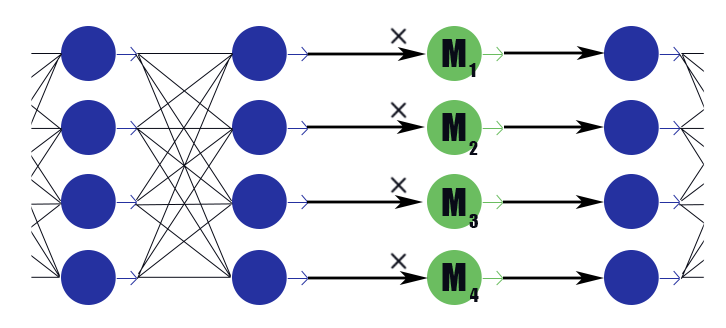
Considere una capa de máscara especial con un vector de peso $$$M = (\ beta_1, \ beta_2, \ dots, \ beta_n)$. Su conclusión es solo un trabajo por partes $$$M$según las conclusiones de la capa anterior, no tiene función de activación. Colocamos en la capa de enmascaramiento después de cada capa, los canales en los que deseamos descartar, y sometemos los pesos en estas capas a la regularización L1. Por lo tanto, el peso de la máscara. $$$\ beta_i$multiplicado por la salida i-ésima de la capa impone implícitamente una restricción en todos los pesos de los que depende esta conclusión. Si entre estos pesos, digamos medio útil, entonces $$$beta_i$se mantendrá más cerca de la unidad, y esta conclusión podrá transmitir bien la información. Pero si solo uno o ninguno en absoluto, $$$beta_i$caerá a cero, lo que restablecerá la salida de la neurona y, de hecho, restablecerá todos los pesos de los que depende esta conclusión (en el caso de la función de activación igual a cero en cero). Tenga en cuenta que de esta manera la red recibe menos refuerzo negativo en el caso de un peso legalmente grande o una respuesta legalmente fuerte. La utilidad de la neurona en su conjunto es importante.

Resulta esta fórmula:

Donde $$$\ lambda$- ponderación constante de pérdida 'una red y pérdida' escasez. Parece la fórmula habitual de regularización L1, solo el segundo término contiene vectores de capas de enmascaramiento, y no el peso de la red.

Después del entrenamiento de la red, revisamos las neuronas y sus valores de enmascaramiento. Si $$$beta_i$más de un cierto umbral, entonces los pesos de las neuronas se multiplican por $$$beta_i$si es menor, entonces los elementos correspondientes a la neurona se eliminan de las matrices de los pesos entrantes y salientes (como en la imagen un poco más arriba). Después de esto, se pueden quitar las máscaras y completar la red.

En la aplicación del grupo LASSO hay varias sutilezas:

1. Regularización normal. Junto con la regularización de los pesos de máscara, la regularización L1 / L2 debe aplicarse a todos los demás pesos de red. Sin esto, una disminución en el peso de enmascaramiento en el caso de funciones de activación no saturadas (ReLu, ELu) se compensará fácilmente con un aumento en los pesos, y el efecto de anulación no funcionará. Sí, y para sigmoide ordinario, esto le permite comenzar mejor el proceso con comentarios positivos: $$$M_i$el resultado no informativo se vuelve más pequeño, por lo que el optimizador tiene que pensar con más fuerza sobre cada peso específico, lo que hace que el resultado sea aún menos informativo, por eso $$$M_i$disminuye aún más y así sucesivamente.
2. Los autores del artículo también aconsejan imponer una restricción esférica sobre el peso de las capas. $$$| W_i | _2 = 1$. Esto probablemente debería contribuir al "flujo" del equilibrio de neuronas débiles a fuertes, pero no noté mucha diferencia.
3. Entrenamiento push-pull. Los autores del artículo sugieren entrenar alternativamente los pesos normales de la red neuronal y los pesos de enmascaramiento. Es más largo que enseñar todo a la vez, pero ¿como si los resultados fueran un poco mejores?
4. No olvide el ajuste fino de la red (ajuste fino) después de arreglar la máscara, esto es muy importante.
5. Controle cuidadosamente el estado de sus máscaras: antes o después de la función de activación. Puede tener problemas con las activaciones que no son iguales a cero cuando el argumento es cero (por ejemplo, un sigmoide).
6. La poda no es amigable con batchnorm por la misma razón que el abandono no es amigable con él: desde el punto de vista de la normalización, cuando hay 32 valores en el paquete 32 de los cuales 12 son cero, y cuando 20 valores en el paquete son situaciones muy diferentes. Después de romper el saldo a cero, la distribución aprendida por la capa de batchnorm deja de ser válida. Debe insertar capas de poda después de todas las capas de batchnorm o modificarlas de alguna manera.
7. También existen dificultades para aplicar la reducción de canales a arquitecturas de ramificación y redes residuales (ResNet). Después de recortar neuronas adicionales durante la fusión de ramas, las dimensiones pueden no coincidir. Esto se resuelve fácilmente mediante la introducción de capas de amortiguación, en las que no rechazamos las neuronas. Además, si las ramas de la red transportan una cantidad diferente de información, tiene sentido establecer diferentes $$$\ lambda$para que no resulte que la poda simplemente corte todas las neuronas en la rama menos informativa. Sin embargo, si todas las neuronas están cortadas, ¿no es esa rama tan importante?
8. En la declaración original del problema, existe una restricción estricta en el número de canales distintos de cero, pero en mi opinión es suficiente para cambiar solo los parámetros de ponderación de la pérdida inicial y la pérdida L1 de los pesos de enmascaramiento, y luego dejar que el optimizador decida cuántos canales dejar.
9. Captura máscaras. Esto no está en el artículo original, pero en mi opinión, este es un buen mecanismo práctico para mejorar la convergencia. Cuando el valor de la máscara alcanza un cierto valor bajo predeterminado, lo reiniciamos y prohibimos cambiar esta parte de la máscara. Por lo tanto, los pesos débiles dejan de contribuir por completo a la predicción durante el entrenamiento del modelo, y no introducen ningún valor perdido en las cantidades correspondientes. Teóricamente, esto puede evitar que un canal potencialmente útil regrese al servicio, pero no creo que esto esté sucediendo en la práctica.

El camino difícil: regularización L0

Pero no estamos buscando formas fáciles, ¿verdad?

El rechazo de canales utilizando la regularización L1 no es del todo justo. Permite que el canal se mueva en la escala de "respuesta fuerte" - "respuesta débil" - "respuesta cero". Solo cuando el peso de enmascaramiento está lo suficientemente cerca de cero, descartamos el canal usando la máscara de captura. Tal movimiento distorsiona enormemente la imagen y realiza cambios en otros canales durante el entrenamiento: antes de que puedan aprender qué hacer cuando la neurona anterior está completamente apagada, deben aprender qué hacer cuando sistemáticamente da una respuesta débil.

Permítame recordarle que, idealmente, nos gustaría seleccionar con entusiasmo el canal menos informativo de la red, continuar aprendiendo la red sin él, eliminar el siguiente canal menos informativo, ajustar la red nuevamente, y así sucesivamente. Desgraciadamente, en tal formulación, la tarea es computacionalmente insoportable incluso para redes relativamente simples. Además, este enfoque no deja a los canales una segunda oportunidad, una vez que una neurona remota no puede volver a funcionar nuevamente. Cambiemos un poco la tarea: a veces eliminaremos la neurona y a veces la dejaremos. Además, si la neurona en su conjunto es útil, se deja con mayor frecuencia, pero si es inútil, viceversa. Para esto, usaremos las mismas capas de enmascaramiento que en el caso de la regularización L1 (¡no fue sin razón por la que se introdujeron!). Solo sus pesos no se moverán a lo largo de todo el eje real con el atractor en cero, sino que se concentrarán alrededor de 0 y 1. No es que se haya vuelto mucho más simple, sino que al menos resolvió el problema de la eliminación categórica de las neuronas.

El instinto del entrenador de la red sugiere que no es necesario resolver el problema mediante una búsqueda exhaustiva, pero debe agregar el número de neuronas activas en las capas en la ejecución actual a la función de pérdida. Sin embargo, dicho término en pérdida será constante por etapas, y el descenso de gradiente no puede funcionar con él. Es necesario enseñar de alguna manera el algoritmo de aprendizaje para excluir periódicamente algunas neuronas, a pesar de la ausencia de un gradiente.

Tenemos una forma de eliminar temporalmente las neuronas: podemos aplicar un abandono a la capa de máscara. Dejar durante el entrenamiento $$$\ beta_i = 1$con probabilidad $$$\ pi$y $$$\ beta_i = 0$con probabilidad $$$1 - \ pi$. Ahora en la función de pérdida puedes poner la suma $$$\ pi$que es un número real Aquí nos enfrentamos a otro obstáculo: la distribución es discreta, no está claro cómo funciona la propagación hacia atrás. En general, existen algoritmos especiales de optimización que pueden ayudarnos aquí (ver REFUERZO), pero adoptaremos un enfoque diferente.

Y luego llegó el momento en que la optimización variacional entra en juego : podemos aproximar la distribución discreta de ceros y unos en la capa de enmascaramiento por una continua y optimizar los parámetros de esta última utilizando el algoritmo de retropropagación habitual. Esta es la idea detrás del trabajo [Aprendizaje de redes neuronales dispersas a través de la regularización L0; Christos Louizos y col .; 2017].

El papel de la distribución continua será desempeñado por la distribución de concreto duro [The Concrete Distribution: A Continuous Relaxation of Discrete Random Variables; Chris Maddison; 2017], aquí hay algo tan complicado de los logaritmos que se aproxima a la distribución de Bernoulli:

$$$\ alpha$- distribución de desplazamiento relativa al centro, y $$$\ beta$- temperatura. En $$$\ beta \ rightarrow 0$La distribución comienza a aproximarse cada vez más a la verdadera distribución de Bernoulli, pero pierde su diferenciabilidad. En $$$0 <\ beta <1$la densidad de distribución es cóncava (este es el caso que nos interesa), para $$$\ beta> 1$- convexo Pasamos esta distribución a través de un sigmoide rígido para que pueda ceder hábilmente con una probabilidad finita distinta de cero $$$z = 0$y $$$z = 1$y en el intervalo (0, 1) tenía una densidad continua diferenciable. Después de terminar la poda, observamos en qué dirección se ha desplazado la distribución y reemplazamos la variable aleatoria $$$z$a un valor de máscara específico $$$\ beta$y traemos a la condición un modelo ya determinista.

Para sentir una distribución un poco mejor, daré algunos ejemplos de su densidad para diferentes parámetros:

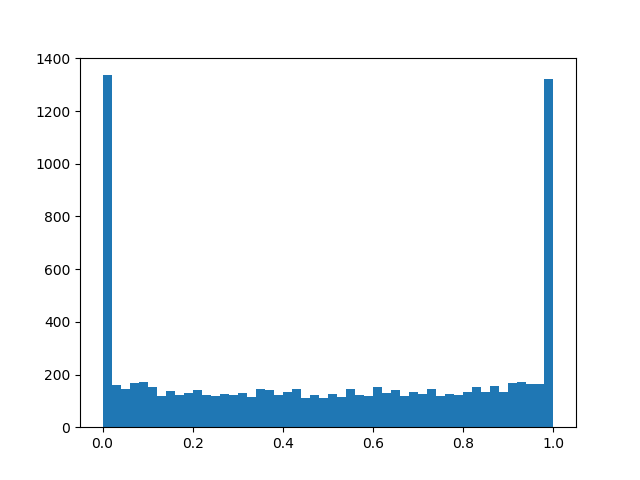
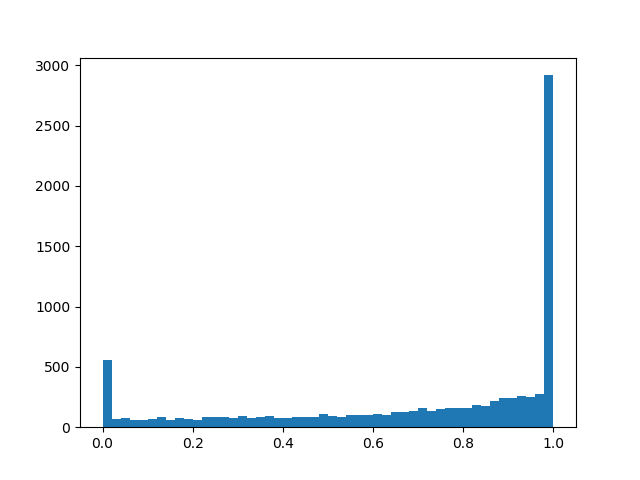
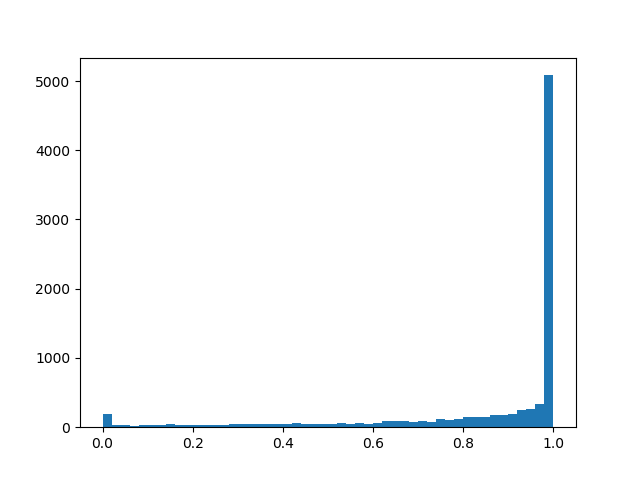
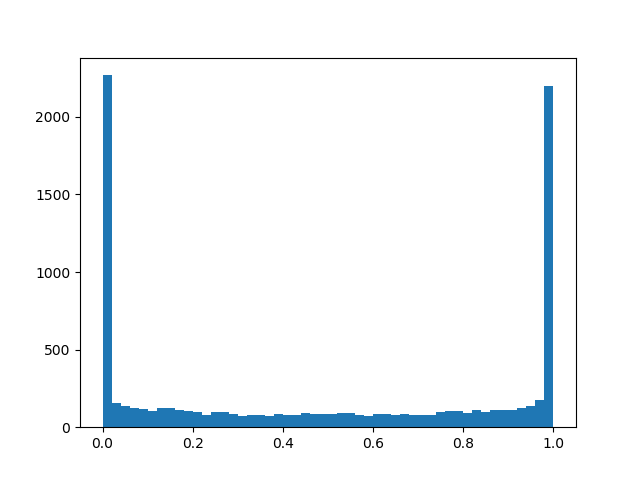
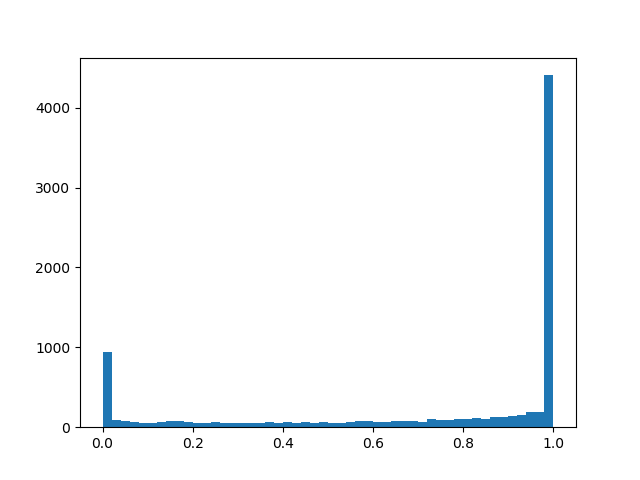
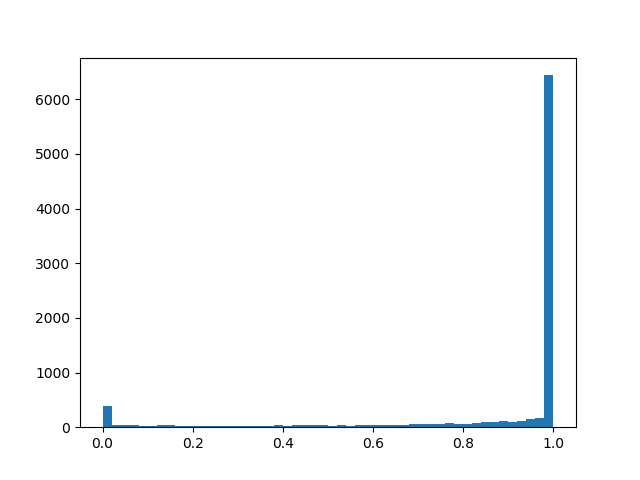
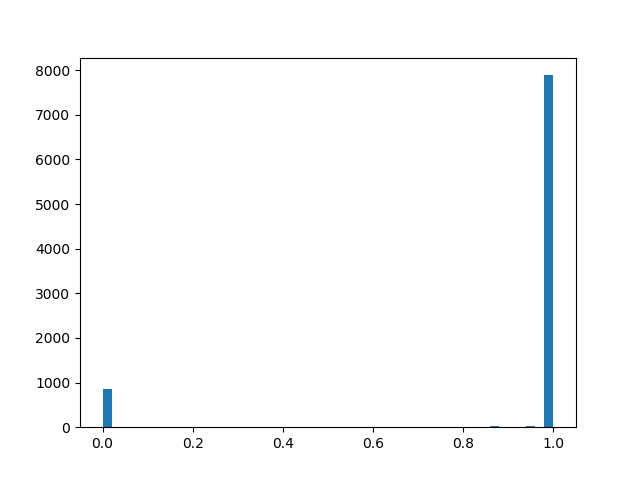
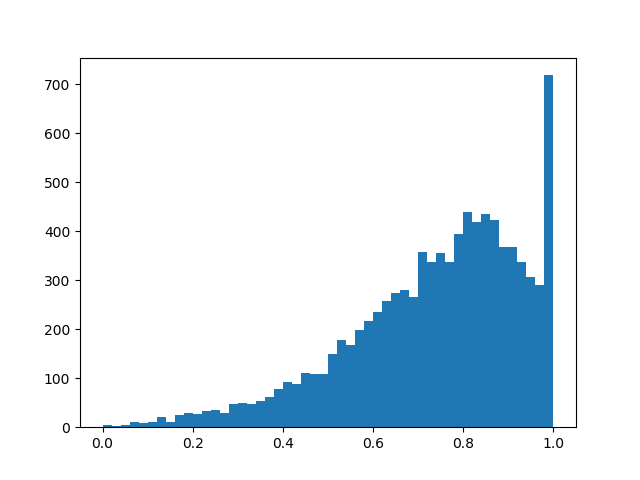
En esencia, tenemos una capa de abandono "inteligente" que aprende qué conclusiones se deben desechar con mayor frecuencia. Pero, ¿qué estamos optimizando exactamente? En caso de pérdida, debe colocar la integral de la densidad de distribución en una región distinta de cero (la probabilidad de que la máscara sea distinta de cero durante el entrenamiento, simplemente):

Las siguientes características se agregan al entrenamiento push-pull, regularización regular y otros detalles de implementación mencionados en el capítulo sobre regularización L1:

• Una vez más: nuestra capa de deserción "inteligente" con una probabilidad notable restablece la salida, con algo, la deja como está, y además, hay una pequeña posibilidad dependiendo de $$$\ beta, \ xi, \ gamma$que la salida se multiplicará por un número aleatorio de 0 a 1. La última parte es más parasitaria que útil para nuestro objetivo final, pero sin ella de ninguna manera, es necesaria para la propagación hacia atrás.
• En general y $$$\ alpha$y $$$\ beta$- parámetros de entrenamiento, pero en mis experimentos sentí que si solo preguntas un poco $$$\ beta$(0.05) y en el proceso de aprendizaje todavía se reduce linealmente, el algoritmo converge mejor que si lo aprende honestamente. $$$\ alpha$es mejor establecer lo suficientemente grande $$$\ log {\ alpha} \ aprox 2.5$de modo que inicialmente las neuronas se conservan más a menudo que se descartan, pero no lo suficientemente grandes como para saturar el sigmoide en pérdida.
• Si se reemplaza en fórmulas $$$\ log {\ alpha}$en solo $$$\ alpha$como si la red estuviera convergiendo mejor y con menos probabilidades de encontrarse con NaN durante el entrenamiento. Con esta maniobra, uno no debe olvidar cambiar el término en la función de pérdida e inicialización.
• Además, si hace trampa y reemplaza el sigmoide habitual en pérdida por uno rígido con restricciones en $$$\ log {\ alpha} \ en [-4, 4]$, la regularización convergerá mejor y actuará más fuerte.
• A $$$\ alpha$y $$$\ beta$También puede aplicar la regularización para aumentar aún más la dispersión.
• Después del entrenamiento, debe binarizar los resultados y entrenar persistentemente la red con la máscara determinada hasta que la precisión val alcance la constante. El artículo proporciona una fórmula más precisa mediante la cual la salida de una neurona puede hacerse determinista durante la validación o para liberar una red, pero parece que al final del entrenamiento $$$\ alpha$resultan estar lo suficientemente polarizados para que funcione una heurística simple: $$$\ alpha <0$- máscara 0, $$$\ alpha \ geq 0$- máscara 1 (pero esto no es exacto). Después de pasar a las máscaras deterministas, verá un salto en la calidad. No olvide que llegamos aquí a cero pesos, y debajo de un cierto umbral de peso, aún necesita reemplazar los pesos de enmascaramiento con ceros.
• Una ventaja adicional del enfoque L0: las capas de enmascaramiento comienzan a funcionar como un abandono, lo que brinda un poderoso efecto de regularización a la red. Pero esta es una espada de doble filo: si comienzas a entrenar con muy poco $$$\ alpha$Existe el riesgo de arruinar la estructura de red pre-entrenada.

Los experimentos

Para el experimento, tomemos el conjunto de datos CIFAR-10 y una red relativamente simple de cuatro capas convolucionales, seguidas por dos completamente conectadas: Conv2D, Máscara, Conv2D, Máscara, Pool2D, Conv2D, Máscara, Conv2D, Máscara, Pool2D, Flatten, Dropout (p = 0.5) , Denso, Máscara, Denso (logits). Se cree que los algoritmos de poda funcionan mejor en redes más gruesas, pero aquí me encontré con un problema puramente técnico de falta de potencia informática. Como optimizador, se utilizó Adam con una tasa de aprendizaje = 0.0015 y un tamaño de lote = 32. Además, se usaron las regularizaciones habituales L1 (0.00005) y L2 (0.00025). No se aplicó el aumento de imagen. La red se entrenó 200 épocas antes de la convergencia, después de lo cual se preservó, y se le aplicaron algoritmos de reducción de neuronas.

Además de aplicar los algoritmos descritos anteriormente para la poda, establecemos un punto de referencia trivial para asegurarnos de que los algoritmos hagan algo. Intentemos tirar el primero de cada capa $$$k$neuronas y terminar la red resultante.

El gráfico muestra los resultados de comparar los algoritmos de reducción de canales L1 y L0 después de una serie de experimentos con diferentes constantes de potencia de regularización. El eje x representa el porcentaje de reducción en el número de pesos después de aplicar el algoritmo. En el eje Y, la precisión de la red de corte en la muestra de validación. La barra azul en el medio es la calidad aproximada de una red que aún no ha sido cortada de neuronas. La línea verde representa un algoritmo de aprendizaje de máscara L1 simple. La línea roja es la poda L0. Línea morada - primer retiro $$$k$canales Triángulos negros: entrenamiento de una red que inicialmente tenía menos pesos.

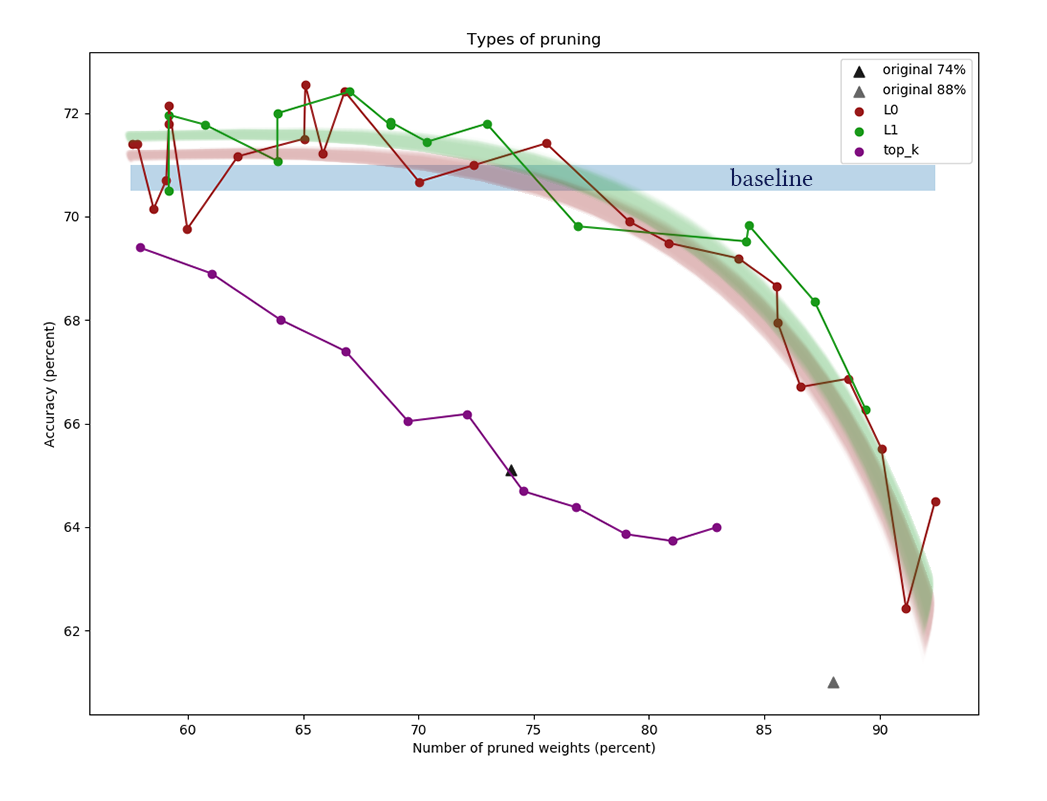
Otro ejemplo para el CIFAR-100 y una red un poco más larga y más amplia de aproximadamente la misma arquitectura y con parámetros de entrenamiento similares:

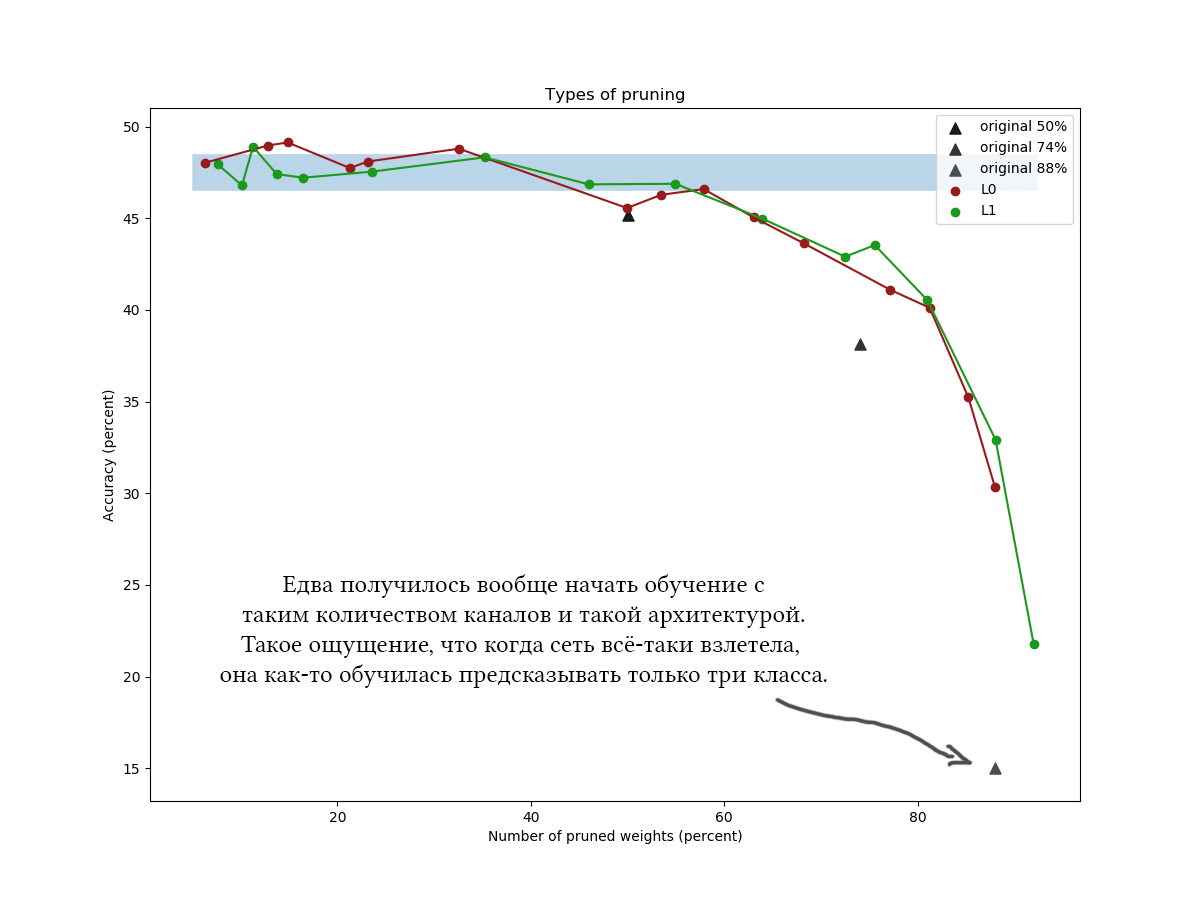
Iiiii en los gráficos es claramente visible que un algoritmo L1 simple no es peor que una astuta optimización variacional, y parece que incluso mejora un poco más la calidad de la red con valores de compresión bajos. Los resultados también se confirman mediante experimentos únicos con otros conjuntos de datos y arquitecturas de red. Este es un resultado absolutamente esperado, con el que contaba cuando comencé a experimentar con la reducción de la red. Honestamente Suspiro

Bueno, para ser sincero, me sorprendió un poco y traté de jugar con el algoritmo y la red: diferentes arquitecturas, hiperparámetros de red, fórmulas exactas, distribución concreta dura, valores iniciales $$$\ alpha$y $$$\ beta$, el número de épocas de sintonización intermedia. La regularización L0 se ve genial en teoría, pero en la práctica es más difícil detectar hiperparámetros, y lleva más tiempo, por lo que no recomendaría usarlo sin experimentos adicionales y procesamiento de archivos. No considere el tiempo dedicado a leer el artículo: la poda L0 parece realmente muy creíble, y diría que prefiero aplicar el algoritmo en algún lugar incorrecto, que no recibí la ganancia prometida. Además, la optimización variacional es la base para algoritmos de reducción aún más avanzados [p. Ej., Compresión de redes neuronales usando el sistema variacional
Cuello de botella de información, 2018].

En general, se pueden sacar las siguientes conclusiones:

1. Muchos canales en la red capacitada son claramente redundantes. Incluso si establece una constante de regularización de máscara pequeña, es fácil lograr una reducción del 30-50% de los pesos. Pero si inicialmente entrenas una grilla demasiado delgada, es difícil lograr buenos resultados. Esto habla a favor del efecto beneficioso de las capas anchas sobre la función objetivo de la red y a favor de la teoría de los boletos de lotería [La hipótesis del boleto de lotería: Entrenamiento de redes neuronales podadas, J. Frankle y M. Carbin, 2018] (cuantas más neuronas, más probabilidades hay de que, aunque si uno de ellos se inicializa para que forme una buena regla).
2. , . . , ?
3. , . 60-90% . $$$k$<7%, .
4. , (<60%) : , !
5. L1 L0 (APoZ), , .. , $$$k$.
6. , . , , , , . , , . pruning' , . - , .

¿Recuerdas cómo escribí al principio de la publicación que después de completar el algoritmo de poda, puedes "simplemente cortar las piezas adicionales de la red por completo"? Por lo tanto, cortar piezas adicionales de la red no es nada fácil. Tensorflow y otras bibliotecas crean un gráfico computacional, y no se puede cambiar tan fácilmente cuando ya está en funcionamiento. Debe guardar la red con las máscaras calculadas, eliminar la lista de los pesos necesarios, transponer los pesos según sea necesario, eliminar los grupos puestos a cero, volver a transponer y crear una nueva red basada en el conjunto de tensores de salida. La red resultante debe tener el mismo diseño que la original, pero tendrá menos neuronas. Espere un dolor de cabeza al mantener el mismo esquema de red en la función de crear la red inicial y final, especialmente si no son lineales, sino ramificadas.

Probablemente para un enmascaramiento conveniente, debe crear sus propias capas. Es fácil, pero tenga cuidado a qué colecciones agrega opciones de enmascaramiento. Es fácil cometer un error y entrenar accidentalmente los parámetros de reducción de canal junto con todas las demás escalas.

Cabe señalar que una parte importante de los pesos de las redes con arquitecturas poco profundas generalmente se concentra en la transición de una parte convolucional a una totalmente conectada. Esto se debe al hecho de que la última capa convolucional se hace plana, como resultado de lo cual, por así decirlo, se forma el (número de canales) * (ancho) * (altura) de las neuronas, y la siguiente matriz de pesos es muy amplia. Es poco probable que estos pesos se corten; además, esto no debe hacerse, de lo contrario las últimas capas de la red estarán "ciegas" a las características que se encuentran en algunos lugares. En tales casos, intente reducir el número final de canales y use maxpool'ing o incluso use arquitecturas totalmente convolucionales o completamente conectadas.

Gracias a todos por su atención, si alguien está interesado en repetir los experimentos con CIFAR-10 y CIFAR-100,el código se puede tomar en github . ¡Que tengas un buen día de trabajo!