Introduccion

Esta breve nota hablará sobre cómo el modelo de dispersión de la luz atmosférica está estructurado en nuestro último 4k int Appear by Jetlag , cuya versión de fiesta ganó un honorable duodécimo lugar en el 4k intro compo en la fiesta de demostración Revision 2018 en abril de este año.

Puede descargar el binario gratis sin SMS aquí .

Sin embargo, si no tiene Windows, o si no tiene una tarjeta de video moderna y potente, entonces hay un tonto reconfortante:

La música para este trabajo fue escrita por Keen usando 4klang . Todo el código y las imágenes quedaron detrás de mí.

Aquí solo hablaremos sobre el modelo de dispersión de luz. Otras cosas, como herramientas, un modelo de ciudad, un modelo de iluminación y materiales, no se ven afectados. Puedo enviar a los valientes a leer la fuente , o ver las grabaciones de cómo me he estado ahogando durante horas : la mayor parte del desarrollo ha sido en video.

Una historia aburrida para perderse

El trabajo en este trabajo comenzó con la comprensión de que el trabajo principal a tiempo completo no deja tiempo para trabajar en un trabajo completo de 4k: ya es casi mediados de marzo en el patio, quedan un par de semanas hasta Revizen.
Solo queda encontrar algo lo suficientemente simple como para un relleno rápido, por un par de noches. Hacer otra estúpida remarcha no es respetar al espectador, así que recordé que hace unos años tuve que hacer un sombreador con dispersión, y era bastante simple, compacto y al mismo tiempo permisible, hermoso, aunque bastante lento.

En el transcurso de una breve discusión, insistí por mi cuenta, y decidimos centrarnos en lo siguiente: hacer un paisaje lleno de luz difusa, con puesta de sol, nubes y rayos crepusculares (TIL como se traduce la expresión "rayos de dios"). Para no elevar el número de pasos en la atmósfera a valores completamente no interactivos, tiene que sonar fuertemente (como un método de patio de Monte Carlo), lo que generará ruido visible. Pero no importa si mueve la cámara y cambia la escena lentamente y comienza la pista ambiental, puede mezclar sin problemas los cuadros adyacentes y suavizar temporalmente este ruido.

Keen escribió la música bastante rápido: estaba casi lista dos semanas antes de la Revisión. Sin embargo, estaba gravemente lisiado por la gripe, con una ambulancia y una enfermedad infecciosa, por lo que prácticamente no comencé a trabajar en el sombreador hasta el momento en que, de alguna manera, más o menos en condiciones de vida, tomé un avión a Frankfurt. El prototipo de este modelo de dispersión ya estaba escrito en el aire.

Preparamos la versión Party del intra de arena y saliva en la fiesta durante las pocas horas restantes antes de la fecha límite (y, probablemente, un par después; D), mientras simultáneamente me alejaba de la gripe, la falta de sueño, los vuelos de horas largas y estaba constantemente distraído al participar en el componente de codificación en vivo de Shader Showdown .

La versión que se muestra en la pantalla grande contenía muchos artefactos y solo la geometría rudimentaria de la ciudad basada en el diagrama de Voronoi con alturas aleatorias.

En general, el duodécimo lugar es bastante generoso.

La versión final, que se muestra arriba, se realizó más tarde y en un modo más relajado, 1-2 pm a la semana durante un mes. En total, tomó alrededor de 40-50 horas de trabajo para trabajar.

Modelo de dispersión

(Nota: no hago programación de gráficos profesionalmente. Este es mi pequeño pasatiempo acogedor para bien, si cien o dos están muy desenfocados bajo cerveza horas de vino al año. Por lo tanto, no hay probabilidad cero de que algunas cosas se describan a continuación y / o se nombren incorrectamente. ¡Tío, golpea!)

El modelo de dispersión está tomado del artículo "Dispersión de luz exterior de alto rendimiento mediante muestreo epipolar" de Egor Yusov , publicado en GPU Pro 5 , con muestreo epipolar completamente expulsado.

Modelo fisico

Los fotones solares bombardean la atmósfera de la Tierra e interactúan con partículas de aire. Un fotón puede ser dispersado por una partícula, lo que implica un cambio en la dirección del fotón, o puede ser absorbido, lo que significa que el fotón se pierde y su energía se ha convertido en alguna otra forma.
Ambos procesos son probabilísticos y dependen en particular de la densidad de partículas y la energía del fotón (que corresponde a su color).

En los dedos, los fotones "rojos" tienen una menor probabilidad de interactuar con el aire, por lo que superan el grosor de la atmósfera relativamente intacto.
Sin embargo, los azules tienen una mayor probabilidad de dispersión, por lo que pueden cambiar de dirección repetidamente y viajar distancias considerables en la atmósfera antes de llegar (o no) al observador.

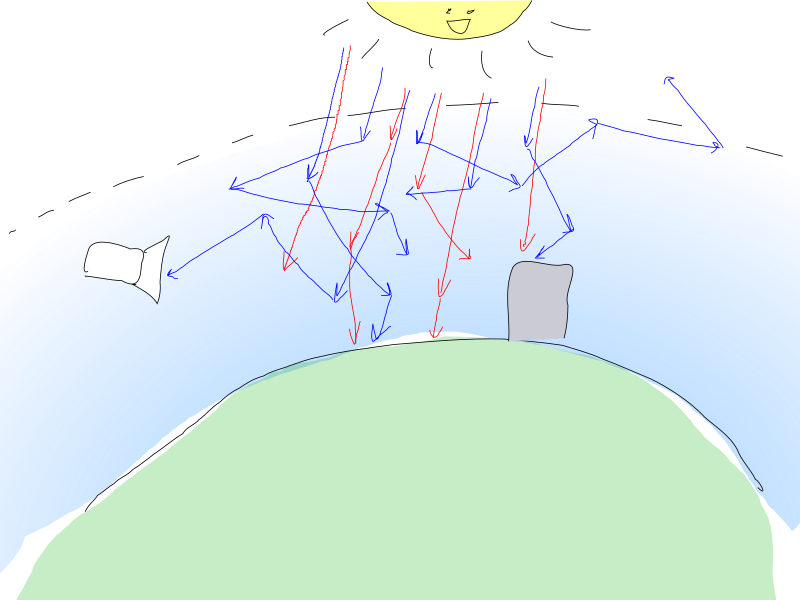
Los parámetros de interacción de la luz con el aire que nos interesan son los siguientes:

• $$$\ beta ^ s (x)$- fracción de luz dispersa por unidad de longitud en un punto $$$x$
• $$$\ beta ^ a (x)$- fracción de luz absorbida por unidad de longitud en un punto $$$x$
• $$$\ beta ^ e (x) = \ beta ^ s (x) + \ beta ^ a (x)$- fracción total de luz perdida por unidad de longitud en un punto $$$x$
• $$$p (\ alpha)$Es la distribución angular de la luz dispersa, donde $$$\ alpha$Este es el ángulo entre el incidente y el haz disperso

Se supone que el aire consta de dos tipos de partículas, cuya dispersión ocurre independientemente: moléculas (modelo de Rayleigh) y aerosoles (partículas esféricas relativamente grandes, dispersión de Mie en la literatura en inglés). Los modelos difieren solo en diferentes valores para los parámetros anteriores.

Para ambos modelos, se cree que la densidad de las partículas correspondientes disminuye exponencialmente con la altura: $$$\ rho = \ rho_0e ^ {- \ frac {h} {H}}$donde $$$\ rho_0$- densidad al nivel del mar. Las probabilidades $$$\ beta$proporcional $$$\ rho$, y sus significados a continuación se dan para el nivel del mar.

Modelo Rayleigh

• $$$p_R (\ alpha) = \ frac {3} {16 \ pi} (1+ \ cos ^ 2 (\ alpha))$[Nishita y col. 93, Preetham y col. 99]
• $$$\ beta_R ^ a = 0$
• $$$\ mathbf {\ beta_R ^ e} = \ mathbf {\ beta_R ^ s} = (5.8, 13.5, 33.1) _ {rgb} 10 ^ {- 6} m ^ {- 1}$[Riley y col. 04, Bruneton y Neyret 08]
• $$$H_R = 7994m$[Nishita y col. 93]

Aerosoles

• $$$p_M (\ alpha) = \ frac {1} {4 \ pi} \ frac {3 (1-g ^ 2)} {2 (2 + g ^ 2)} \ frac {1+ \ cos ^ 2 (\ alfa)} {(1 + g ^ 2 - 2g \ cos (\ alpha)) ^ \ frac {3} {2}}$[Nisita y col. 93, Riley y col. 04] donde $$$g = 0.76$[Bruneton y Neyret 08]
• $$$\ beta_M ^ s = 2 \ cdot10 ^ {- 5} m ^ {- 1}$[Bruneton y Neyret 08]
• $$$\ beta_M ^ e = 1.1 \ beta_M ^ s$
• $$$H_M = 1200m$[Nishita y col. 93]

Aproximación de dispersión única

La aproximación de dispersión se basa en la emisión de un haz desde cada píxel de la cámara y el cálculo de cuánta luz de la atmósfera debería recibir desde esta dirección. Cada rayo corresponde a los tres componentes de luz RGB, como si tres fotones con energías correspondientes vuelen a lo largo de este rayo.

La luz que llega a la cámara está formada por los siguientes procesos en el aire:

• Dispersión (TIL que los higos aprenden a traducir en dispersión). Se agrega la luz emitida por el sol, que se dispersa probabilísticamente en un ángulo correspondiente a la dirección de la cámara.
• Absorción La luz que ya vuela a lo largo del rayo es absorbida por el aire.
• Dispersión La luz que ya vuela a lo largo del rayo se pierde al dispersarse en otras direcciones.

Por razones de rendimiento, creemos que la luz solo puede entrar en la dirección de la cámara desde la dispersión una vez, y toda otra luz (que se dispersó más de una vez) puede descuidarse. Esto no se recomienda para el crepúsculo, pero qué hacer.

Este enfoque se representa en la siguiente imagen hermosa (¡lo intenté!):

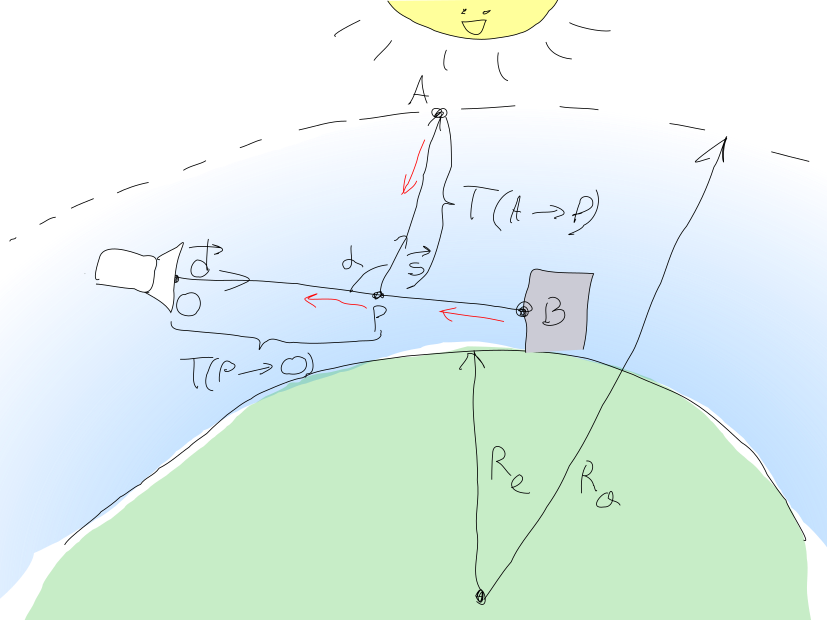
Por lo tanto, la cantidad de luz que debe detectar el píxel de la cámara en $$$O$se puede calcular como la suma $$$\ mathbf {L} = \ mathbf {L_ {in}} + \ mathbf {L_ {BO}}$donde $$$\ mathbf {L_ {in}}$- luz difusa del sol, y $$$\ mathbf {L_ {BO}}$- la cantidad de luz desde el punto $$$B$escena de geometría de objeto llegando $$$O$.

Geometría ligera

$$$\ mathbf {L_ {BO}} = \ mathbf {L_O} e ^ {- \ mathbf {T} (B \ rightarrow O)}$donde $$$\ mathbf {L_O}$¿Se emite la luz desde un punto? $$$B$hacia la cámara.

$$$\ mathbf {T} (B \ rightarrow O)$llamado el espesor óptico del medio entre los puntos $$$B$y $$$O$, y se calcula de la siguiente manera:

$$

$$\ mathbf {T} (B \ rightarrow O) = \ int_B ^ O (\ beta_M ^ e (s) + \ mathbf {\ beta_R ^ e} (s)) ds$$

Mientras que los miembros $$$\ beta$constan de nivel constante del mar y densidad variable, esta expresión se puede convertir a:

$$

$$\ mathbf {T} (B \ rightarrow O) = \ beta_M ^ e \ cdot \ int_B ^ O \ rho_M (s) ds + \ mathbf {\ beta_R ^ e} \ int_B ^ O \ rho_R (s) ds = \ bar {\ mathbf {\ beta}} \ cdot \ bar {T_ \ rho} (B \ rightarrow O)$$

Tenga en cuenta que no divulgo específicamente $$$\ rho$, porque los cambiaremos más adelante cuando agreguemos nubes. También llamo la atención sobre el hecho de que $$$\ beta$- Vectores RGB (al menos $$$\ mathbf {\ beta_R}$tener diferentes significados para los componentes RGB, y $$$\ beta_M$- vector solo por consistencia). Miembros con $$$\ rho$debajo de la integral están los escalares.

Sol

Sol $$$\ mathbf {L_ {in}}$calculado por integración sobre todos los puntos $$$P$a lo largo del segmento $$$Ob$y la acumulación de toda la luz solar entrante dispersándose hacia la cámara y muriendo en el espesor $$$\ mathbf {T} (P \ rightarrow O)$.

La cantidad de luz solar que alcanza un punto $$$P$se calcula con una fórmula similar $$$\ mathbf {L_P} = \ mathbf {L_ {sun}} e ^ {- T (A \ rightarrow P)}$donde $$$\ mathbf {L_ {sun}}$- el brillo del sol, y $$$A$Es el punto en el que el rayo desde el punto $$$P$hacia el sol $$$\ vec {s}$deja el ambiente La fracción de esta luz que se dispersará hacia la cámara es $$$\ mathbf {L_P} \ cdot (\ mathbf {\ beta_R ^ s} (s) p_R (\ alpha) + \ beta_M ^ s (s) p_M (\ alpha))$.

Total que obtenemos:

$$

$$\ mathbf {L_ {in}} = \ int_B ^ O \ mathbf {L_P} (s) \ cdot (\ beta_M ^ s (s) p_M (\ alpha) + \ mathbf {\ beta_R ^ s} (s) p_R (\ alpha)) \ cdot e ^ {- \ mathbf {T} (P (s) \ rightarrow O)} ds$$

Puede notar que:

• $$$\ alpha$es una constante para cada píxel-rayo de la cámara (creemos que el sol está infinitamente lejos y que los rayos son paralelos)
• Las probabilidades $$$\ beta$consisten en constantes de nivel del mar y funciones de densidad $$$\ rho (s)$
• Las funciones $$$p (\ alpha)$tienen factores comunes para ambos procesos de dispersión

Esto le permite convertir la expresión a:

$$

$$\ mathbf {L_ {in}} = \ mathbf {L_ {sun}} (1+ \ cos ^ 2 (\ alpha)) (\ frac {\ frac {1} {4 \ pi} \ frac {3 (1 -g ^ 2)} {2 (2 + g ^ 2)}} {(1 + g ^ 2 - 2g \ cos (\ alpha)) ^ \ frac {3} {2}} \ beta_M ^ s \ cdot \ mathbf {I_M} + \ frac {3} {16 \ pi} \ mathbf {\ beta_R ^ s} \ cdot \ mathbf {I_R})$$

donde

$$

$$\ mathbf {I_M} = \ int_B ^ O \ rho_M (s) e ^ {- \ mathbf {T} (A \ rightarrow P (s)) - \ mathbf {T} (P (s) \ rightarrow O)} ds$$

$$

$$\ mathbf {I_R} = \ int_B ^ O \ rho_R (s) e ^ {- \ mathbf {T} (A \ rightarrow P (s)) - \ mathbf {T} (P (s) \ rightarrow O)} ds$$

$$$I_m$y $$$I_R$difieren solo en las funciones de densidad; sus exponenciales son las mismas.

Nadie logró calcular estas integrales de forma analítica, por lo que deben calcularse numéricamente mediante el mapeo (como dicen en las publicaciones originales, ¡no puede hacerlo!).

Integración numérica

Por razones de tamaño y pereza, lo consideraremos lo más estúpido posible: $$$\ int_A ^ B f (x) dx \ approx \ frac {\ left | B - A \ right |} {N} \ sum_ {i = 0} ^ N f (A + i \ cdot \ frac {\ vec { B - A}} {N})$

La marcha de rayos se realizará en la dirección opuesta al flujo de luz: desde el punto de la cámara $$$O$antes de la intersección de la viga con geometría $$$B$. Segmento de línea $$$O \ rightarrow B$dividido por $$$N$pasos

Antes de comenzar la marcha, inicialice las variables:

• vec2 (dos componentes separados, para dispersión de Rayleigh y aerosol) espesor óptico total acumulado $$$\ mathbf {T_ \ rho} (P (s) \ rightarrow O)$
• vec3 (RGB) $$$\ mathbf {I_M}$, $$$\ mathbf {I_R}$

Siguiente para el punto $$$P_i$cada paso entre $$$O$y $$$B$:

1. Rayamos $$$\ vec {s}$en la dirección del sol y obtener un punto $$$A_i$La salida de este rayo de la atmósfera.
2. Calcular el espesor $$$\ mathbf {T} (A \ rightarrow P_i)$calculando primero $$$\ int_A ^ {P_i} \ rho_M (s) ds$y $$$\ int_A ^ {P_i} \ rho_R (s) ds$usando la misma remarcha (con el número de pasos M ), y luego multiplique los términos resultantes con las constantes correspondientes $$$\ beta_M ^ e$y $$$\ mathbf {\ beta_R ^ e}$.
3. Calcular el espesor $$$\ mathbf {T_ \ rho} (P_i \ rightarrow O) = \ mathbf {T_ \ rho} (P_ {i-1} \ rightarrow O) + \ rho_i (s) \ cdot ds$
4. Acumular $$$\ mathbf {I_R}$y $$$\ mathbf {I_M}$usando estos valores

El color final después de volver a buscar se calcula mediante la suma de los términos:

1. Plazo $$$\ mathbf {L_ {BO}}$obtener trivial: una variable que contiene $$$\ mathbf {T_ \ rho} (P_i \ rightarrow O)$contiene valor $$$\ mathbf {T_ \ rho} (B \ rightarrow O)$desde $$$P_i$ha alcanzado $$$B$.
2. Por multiplicación $$$\ mathbf {I_R}$y $$$\ mathbf {I_M}$a las constantes correspondientes y al sumar el resultado se calcula $$$\ mathbf {L_ {in}}$

Sombreadores

Dispersión simple sin nadie

Fuentes de dispersión ligeramente peinadas y comentadas tomadas (casi) directamente de la propia intra:

 const float R0 = 6360e3; //    const float Ra = 6380e3; //     const vec3 bR = vec3(58e-7, 135e-7, 331e-7); //    const vec3 bMs = vec3(2e-5); //    const vec3 bMe = bMs * 1.1; const float I = 10.; //   const vec3 C = vec3(0., -R0, 0.); //   ,  (0, 0, 0)    //   //  vec2(rho_rayleigh, rho_mie) vec2 densitiesRM(vec3 p) { float h = max(0., length(p - C) - R0); //    return vec2(exp(-h/8e3), exp(-h/12e2)); } //    ,        float escape(vec3 p, vec3 d, float R) { vec3 v = p - C; float b = dot(v, d); float det = b * b - dot(v, v) + R*R; if (det < 0.) return -1.; det = sqrt(det); float t1 = -b - det, t2 = -b + det; return (t1 >= 0.) ? t1 : t2; } //         `L`   `p`   `d` //   `steps`  //  vec2(depth_int_rayleigh, depth_int_mie) vec2 scatterDepthInt(vec3 o, vec3 d, float L, float steps) { vec2 depthRMs = vec2(0.); L /= steps; d *= L; for (float i = 0.; i < steps; ++i) depthRMs += densitiesRM(o + d * i); return depthRMs * L; } //   (  --   ) vec2 totalDepthRM; vec3 I_R, I_M; //    vec3 sundir; //    ,    `-d`   `L`   `o`   `d`. // `steps` --    void scatterIn(vec3 o, vec3 d, float L, float steps) { L /= steps; d *= L; //   O  B for (float i = 0.; i < steps; ++i) { // P_i vec3 p = o + d * i; vec2 dRM = densitiesRM(p) * L; //  T(P_i -> O) totalDepthRM += dRM; //     T(P_i ->O) + T(A -> P_i) // scatterDepthInt()    T(A -> P_i) vec2 depthRMsum = totalDepthRM + scatterDepthInt(p, sundir, escape(p, sundir, Ra), 4.); vec3 A = exp(-bR * depthRMsum.x - bMe * depthRMsum.y); I_R += A * dRM.x; I_M += A * dRM.y; } } //    // O = o --   // B = o + d * L --   // Lo --     B vec3 scatter(vec3 o, vec3 d, float L, vec3 Lo) { totalDepthRM = vec2(0.); I_R = I_M = vec3(0.); //  T(P -> O) and I_M and I_R scatterIn(o, d, L, 16.); // mu = cos(alpha) float mu = dot(d, sundir); //     return Lo * exp(-bR * totalDepthRM.x - bMe * totalDepthRM.y) //   + I * (1. + mu * mu) * ( I_R * bR * .0597 + I_M * bMs * .0196 / pow(1.58 - 1.52 * mu, 1.5)); } 

Cállate en el sombreador

Las nubes

No está mal, pero esa imagen también podría obtenerse mucho más fácilmente con un montón de gradientes astutos.

De manera engañosa, obtener nubes y rayos de Dios es mucho más difícil. Vamos a agregar

La idea es aproximar las nubes con aerosoles y modificar solo la función de densitiesRM() . Esto puede no ser tan físicamente correcto como nos gustaría (no tengo idea de cómo se aproxima realmente la dispersión de la luz en las nubes en los gráficos por computadora).

 //      const float low = 1e3, hi = 25e2; // vec4 noise24(vec2 v) --       // float t --  float noise31(vec3 v) { return (noise24(v.xz).x + noise24(v.yx).y) * .5; } vec2 densitiesRM(vec3 p) { float h = max(0., length(p - C) - R0); vec2 retRM = vec2(exp(-h/8e3), exp(-h/12e2) * 8.); //    () if (low < h && h < hi) { vec3 v = 15e-4 * (p + t * vec3(-90., 0., 80.)); //    <s></s>      :     retRM.y += 250. * step(vz, 38.) * smoothstep(low, low + 1e2, h) * smoothstep(hi, hi - 1e3, h) * smoothstep(.5, .55, //  :   .75 * noise31(v) + .125 * noise31(v*4. + t) + .0625 * noise31(v*9.) + .0625 * noise31(v*17.)-.1 ); } return retRM; } 

Contrariamente a lo esperado, no obtenemos nubes hermosas, una dulce victoria y fanáticos, sino artefactos. Intentar aumentar la cantidad de pasos que los artefactos en la frente no eliminan por completo, pero estropea significativamente el rendimiento.

Soluciones muletas que empujan el intra:

• Los artefactos más desagradables en el horizonte se esconden detrás de las montañas.
• Las nubes se agregan solo cerca de la cámara.
• Se agrega Monte-Karlovschina, cada rayo de marcha se desplaza por un desplazamiento aleatorio: for (float i = pixel_random.w; i < steps; ++i) . Esto se suma al ruido que tiene que suavizar temporalmente al mezclar cuadros sucesivos.

• El número de pasos para zonas que requieren más detalles está aumentando (por ejemplo, una capa con nubes). Es por esto que se hace una separación tan absurda de funciones en scatterImpl() y scatterDepthInt() :

  
  

   //    scatterIn() vec2 depthRMsum = totalDepthRM; float l = max(0., escape(p, sundir, R0 + hi)); if (l > 0.) //   16  depthRMsum += scatterDepthInt(p, sundir, l, 16.); //     4- depthRMsum += scatterDepthInt(p + sundir * l, sundir, escape(p, sundir, Ra), 4.); 

  
  

   //   scatter() //  10    float l = 10e3; if (L < l) scatterIn(o, d, L, 16.); else { scatterIn(o, d, l, 32.); // 8  --     scatterIn(o+d*l, d, Ll, 8.); } 

  
  

Alineación con la geometría de la escena.

Como resultado de la reasignación tradicional de las funciones de distancia y sombra, la distancia L al punto B y el color de píxel Lo ya se han obtenido. Estos valores simplemente se sustituyen en la función scatter() . Si el rayo no descansa contra la geometría y abandona la escena, entonces el color Lo cero, y L calcula usando escape() : se cree que el rayo ha abandonado la atmósfera.

Como todo

... De hecho, por supuesto, no todos. Es un gran dolor frotar todas las partes para que parezca creíble. Solo un montón de alboroto con parámetros de torsión, geometría de escena, funciones de ruido, trayectoria y ángulo de cámara. Me temo que no tengo buenos consejos aquí, excepto por repetir muchas horas y golpear mi cabeza contra la pared.

Minificación

Después de procesar el minificador de sombreador , el código de dispersión del sombreador final tiene un tamaño de aproximadamente 1500 bytes. Crinkler lo comprime a ~ 700 bytes, que es aproximadamente el 30% de todo el código del sombreador.

La cría

No sé cómo hacer gráficos por computadora.