Si describe en un par de oraciones sobre qué principios de intercambio de clasificación funcionan, entonces:

1. Los elementos de la matriz se comparan en pares
2. Si el elemento a la izquierda ^{* es} más grande que el elemento a la derecha, entonces los elementos se intercambian
3. Repita los pasos 1 y 2 hasta que la matriz esté ordenada

^{* - el elemento de la izquierda significa ese elemento del par comparado, que está más cerca del borde izquierdo de la matriz. En consecuencia, el elemento de la derecha está más cerca del borde derecho.}

Pido disculpas de inmediato por repetir material conocido, es poco probable que al menos uno de los algoritmos del artículo sea una revelación para usted. Sobre estas clasificaciones en Habré, ya se escribió muchas veces (incluyéndome a mí - 1 , 2 , 3 ) y pregunta por qué nuevamente volver a este tema. Pero como decidí escribir una serie coherente de artículos sobre todas las clasificaciones en el mundo , tengo que seguir los métodos de intercambio incluso en la versión express. Al considerar las siguientes clases, ya habrá muchos algoritmos nuevos (y pocas personas lo saben) que merecen artículos interesantes por separado.

Tradicionalmente, los "intercambiadores" incluyen clasificaciones en las que los elementos cambian (pseudo) aleatoriamente (bogosort, bozosort, permsort, etc.). Sin embargo, no los incluí en esta clase, ya que carecen de comparaciones. Habrá un artículo separado sobre estas clasificaciones, donde filosofaremos mucho sobre la teoría de la probabilidad, la combinatoria y la muerte térmica del Universo.

Tipo tonto :: Tipo de títere

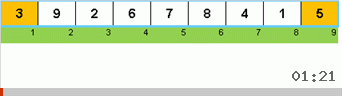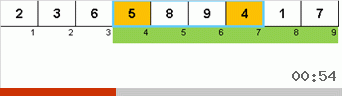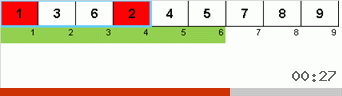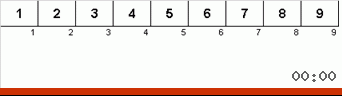
1. Compare (y, si es necesario, cambie) los elementos en los extremos de la submatriz.
2. Tomamos dos tercios de la submatriz desde su comienzo y aplicamos el algoritmo general a estos 2/3 de forma recursiva.
3. Tomamos dos tercios de la submatriz desde su final y aplicamos el algoritmo general a estos 2/3 de forma recursiva.
4. Y nuevamente, tomamos dos tercios de la submatriz desde su comienzo y aplicamos el algoritmo general a estos 2/3 de forma recursiva.

Inicialmente, una submatriz es una matriz completa. Y luego, la recursión divide el subconjunto principal en 2/3, realiza comparaciones / intercambios en los extremos de los segmentos fragmentados y, finalmente, organiza todo.

def stooge_rec(data, i = 0, j = None): if j is None: j = len(data) - 1 if data[j] < data[i]: data[i], data[j] = data[j], data[i] if j - i > 1: t = (j - i + 1) // 3 stooge_rec(data, i, j - t) stooge_rec(data, i + t, j) stooge_rec(data, i, j - t) return data def stooge(data): return stooge_rec(data, 0, len(data) - 1) 

Parece esquizofrénico, pero sin embargo es 100% correcto.

Clasificación lenta :: Clasificación lenta

Y aquí observamos el misticismo recursivo:

1. Si la submatriz consta de un elemento, entonces completamos la recursividad.
2. Si una submatriz consta de dos o más elementos, divídala por la mitad.
3. Aplicamos el algoritmo recursivamente a la mitad izquierda.
4. Aplicamos el algoritmo recursivamente a la mitad derecha.
5. Los elementos en los extremos de la submatriz se comparan (y cambian si es necesario).
6. Aplicamos recursivamente el algoritmo a una submatriz sin el último elemento.

Inicialmente, una submatriz es toda la matriz. Y la recursión continuará reduciéndose a la mitad, comparándola y cambiando hasta que resolvió todo.

 def slow_rec(data, i, j): if i >= j: return data m = (i + j) // 2 slow_rec(data, i, m) slow_rec(data, m + 1, j) if data[m] > data[j]: data[m], data[j] = data[j], data[m] slow_rec(data, i, j - 1) def slow(data): return slow_rec(data, 0, len(data) - 1) 

Parece una tontería, pero la matriz está ordenada.

¿Por qué funcionan correctamente StoogeSort y SlowSort?

Un lector curioso hará una pregunta razonable: ¿por qué funcionan estos dos algoritmos? Parecen simples, pero no es muy obvio que puedas ordenar algo así.

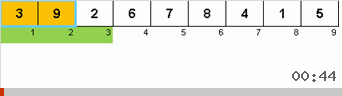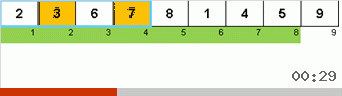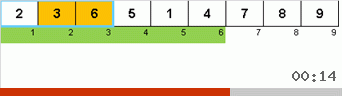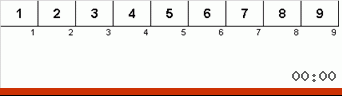
Primero echemos un vistazo a la clasificación lenta. El último punto de este algoritmo insinúa que los esfuerzos recursivos de la clasificación lenta solo tienen como objetivo colocar el elemento más grande en el subconjunto en la posición más a la derecha. Esto es especialmente notable si aplica el algoritmo a una matriz reordenada:



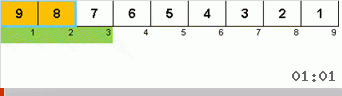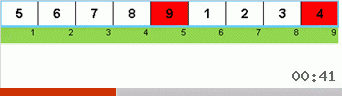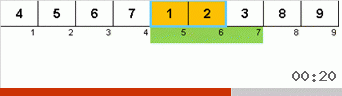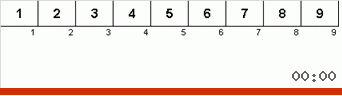
Se ve claramente que en todos los niveles de recursión, los máximos migran rápidamente hacia la derecha. Luego, estos máximos, donde están donde se necesitan, se desactivan del juego: el algoritmo se llama a sí mismo, pero sin el último elemento.

En el tipo Stooge, ocurre una magia similar:



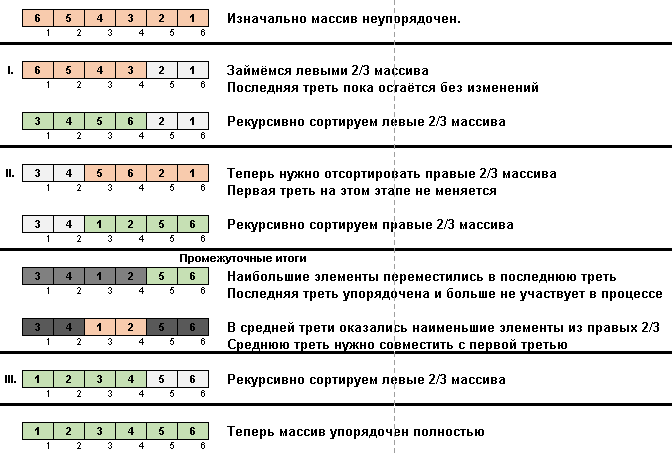
De hecho, también se pone énfasis en los elementos máximos. Solo la ordenación lenta los mueve al final uno por uno, y la ordenación Stooge empuja un tercio de los elementos del subarreglo (el más grande de ellos) empuja hacia el tercio derecho del espacio de la celda.

Pasamos a los algoritmos, donde todo ya es bastante obvio.

Dumb Sort :: Stupid sort

Muy cuidadosa clasificación. Va desde el principio de la matriz hasta el final y compara los elementos vecinos. Si dos elementos vecinos tuvieran que intercambiarse, entonces, por si acaso, la ordenación regresa al comienzo de la matriz y comienza de nuevo.

 def stupid(data): i, size = 1, len(data) while i < size: if data[i - 1] > data[i]: data[i - 1], data[i] = data[i], data[i - 1] i = 1 else: i += 1 return data 

Gnome sort :: Gnome sort

Casi lo mismo, pero la clasificación durante el intercambio no vuelve al comienzo de la matriz, sino que solo retrocede un paso. Resulta que esto es suficiente para resolver todo.

 def gnome(data): i, size = 1, len(data) while i < size: if data[i - 1] <= data[i]: i += 1 else: data[i - 1], data[i] = data[i], data[i - 1] if i > 1: i -= 1 return data 

Ordenamiento enano optimizado

Pero puede ahorrar no solo en la retirada, sino también al avanzar. Con varios intercambios consecutivos, debe retroceder tantos pasos. Y luego tienes que regresar (comparando en el camino los elementos que ya están ordenados entre sí). Si recuerda la posición desde la que comenzaron los intercambios, puede saltar inmediatamente a esta posición cuando se completen los intercambios.

 def gnome(data): i, j, size = 1, 2, len(data) while i < size: if data[i - 1] <= data[i]: i, j = j, j + 1 else: data[i - 1], data[i] = data[i], data[i - 1] i -= 1 if i == 0: i, j = j, j + 1 return data 

Clasificación de burbujas :: Clasificación de burbujas

A diferencia de la clasificación estúpida y gnómica, cuando se intercambian elementos en la burbuja, no se producen devoluciones, continúa avanzando. Al llegar al final, el elemento más grande de la matriz se mueve hasta el final.

Luego, el proceso de clasificación repite todo el proceso nuevamente, como resultado de lo cual el segundo elemento en la antigüedad está en el último pero un lugar. En la siguiente iteración, el tercer elemento más grande es el tercero desde el final, etc.

 def bubble(data): changed = True while changed: changed = False for i in range(len(data) - 1): if data[i] > data[i+1]: data[i], data[i+1] = data[i+1], data[i] changed = True return data 

Clasificación optimizada de burbujas

Puede beneficiarse un poco en los pasillos al comienzo de la matriz. En el proceso, los primeros elementos se ordenan temporalmente entre sí (esta parte ordenada cambia constantemente de tamaño, disminuye, aumenta). Esto se soluciona fácilmente y con una nueva iteración simplemente puede saltar sobre un grupo de tales elementos.
_{(Agregaré la implementación probada en Python aquí un poco más tarde. No tuve tiempo de prepararla).}

Shaker Sort :: Shaker sort
(Cóctel tipo :: Cóctel tipo)

Una especie de burbuja En la primera pasada, como siempre, empuje el máximo hasta el final. Luego giramos bruscamente y empujamos el mínimo al principio. Las áreas marginales ordenadas de la matriz aumentan de tamaño después de cada iteración.

 def shaker(data): up = range(len(data) - 1) while True: for indices in (up, reversed(up)): swapped = False for i in indices: if data[i] > data[i+1]: data[i], data[i+1] = data[i+1], data[i] swapped = True if not swapped: return data 

Clasificación par impar :: Clasificación par impar

Nuevamente, iteraciones sobre la comparación por pares de elementos vecinos cuando se mueve de izquierda a derecha. Solo primero, compare los pares en los que el primer elemento es impar en el recuento, y el segundo es par (es decir, el primero y el segundo, el tercero y el cuarto, el quinto y el sexto, etc.). Y luego viceversa: par + impar (segundo y tercero, cuarto y quinto, sexto y séptimo, etc.). En este caso, muchos elementos grandes de la matriz en una iteración al mismo tiempo dan un paso adelante (en la burbuja, el más grande para la iteración llega al final, pero el resto de los más grandes casi permanecen en su lugar).

Por cierto, esto era originalmente un tipo paralelo con O (n) complejidad. Será necesario implementar AlgoLab en la sección "Clasificación paralela".

 def odd_even(data): n = len(data) isSorted = 0 while isSorted == 0: isSorted = 1 temp = 0 for i in range(1, n - 1, 2): if data[i] > data[i + 1]: data[i], data[i + 1] = data[i + 1], data[i] isSorted = 0 for i in range(0, n - 1, 2): if data[i] > data[i + 1]: data[i], data[i + 1] = data[i + 1], data[i] isSorted = 0 return data 

Peine Ordenar :: Peine ordenar

La modificación más exitosa de la burbuja. El algoritmo de velocidad compite con la clasificación rápida.

En todas las variaciones anteriores, comparamos a los vecinos. Y aquí, primero, se consideran pares de elementos que están a una distancia máxima entre sí. En cada nueva iteración, esta distancia se estrecha de manera uniforme.

 def comb(data): gap = len(data) swaps = True while gap > 1 or swaps: gap = max(1, int(gap / 1.25)) # minimum gap is 1 swaps = False for i in range(len(data) - gap): j = i + gap if data[i] > data[j]: data[i], data[j] = data[j], data[i] swaps = True return data 

Clasificación rápida :: Clasificación rápida

Bueno, el algoritmo de intercambio más avanzado.

1. Divide la matriz por la mitad. El elemento del medio es la referencia.
2. Nos movemos desde el borde izquierdo de la matriz hacia la derecha, hasta que encontramos un elemento que es más grande que el de referencia.
3. Nos movemos desde el borde derecho de la matriz hacia la izquierda hasta que encontramos un elemento que es más pequeño que el de referencia.
4. Intercambiamos los dos elementos encontrados en los puntos 2 y 3.
5. Continuamos llevando a cabo los puntos 2-3-4 hasta que se produzca una reunión como resultado del movimiento mutuo.
6. En el punto de encuentro, la matriz se divide en dos partes. Para cada parte, aplicamos recursivamente un algoritmo de ordenación rápida.

Por que funciona A la izquierda del punto de encuentro hay elementos más pequeños o iguales que el de referencia. A la derecha del punto de encuentro hay elementos mayores o iguales a la referencia. Es decir, cualquier elemento del lado izquierdo es menor o igual que cualquier elemento del lado derecho. Por lo tanto, en el punto de encuentro, la matriz se puede dividir de forma segura en dos submatrices y ordenar cada submatriz de manera recursiva similar.

 def quick(data): less = [] pivotList = [] more = [] if len(data) <= 1: return data else: pivot = data[0] for i in data: if i < pivot: less.append(i) elif i > pivot: more.append(i) else: pivotList.append(i) less = quick(less) more = quick(more) return less + pivotList + more 

K-sort :: K-sort

En Habré se publica una traducción de uno de los artículos, que informa sobre la modificación de QuickSort, que supera la clasificación piramidal en 7 millones de elementos. Por cierto, esto en sí mismo es un logro dudoso, porque la clasificación piramidal clásica no rompe los registros de rendimiento. En particular, su complejidad asintótica en ningún caso alcanza O (n) (una característica de este algoritmo).

Pero la cosa es diferente. Según el pseudocódigo del autor (y obviamente incorrecto), generalmente no es posible entender cuál es, de hecho, la idea principal del algoritmo. Personalmente, tuve la impresión de que los autores son unos delincuentes que actuaron de acuerdo con este método:

1. Declaramos la invención de un algoritmo de super-clasificación.
2. Reforzamos la declaración con un pseudocódigo incomprensible que no funciona (como, inteligente y muy claro, pero los tontos aún no pueden entenderlo).
3. Presentamos gráficos y tablas que supuestamente demuestran la velocidad práctica del algoritmo en big data. Debido a la falta de un código que realmente funcione, nadie podrá verificar ni refutar estos cálculos estadísticos.
4. Publicamos tonterías en Arxiv.org bajo la apariencia de un artículo científico.
5. BENEFICIO !!!

¿Tal vez estoy hablando en vano con la gente y, de hecho, el algoritmo está funcionando? ¿Alguien puede explicar cómo funciona k-sort?

UPD Mis amplias acusaciones de seleccionar autores de fraude resultaron ser infundadas :) El usuario jetsys descubrió el pseudocódigo del algoritmo, escribió una versión funcional en PHP y me lo envió en mensajes privados:

Anuncio

Todo era una teoría, es hora de pasar a la práctica. El siguiente artículo está probando intercambios de clasificación en diferentes conjuntos de datos. Descubriremos:

• ¿Qué clasificación es la peor: tonta, aburrida o aburrida?
• ¿Las optimizaciones y modificaciones a la clasificación de burbujas realmente ayudan?
• ¿En qué condiciones los algoritmos lentos son fácilmente rápidos en la velocidad de QuickSort?

Y cuando descubramos las respuestas a estas preguntas más importantes, podemos comenzar a estudiar la próxima clase: los tipos de inserción.

Referencias

Aplicación de Excel AlgoLab , con la que puede ver paso a paso la visualización de estos (y no solo estos) tipos.

Wiki - Silly / Stooge , Slow , Dwarf / Gnome , Bubble / Bubble , Shaker / Shaker , Odd / Even , Comb / Comb , Fast / Quick

Artículos de la serie

• Aplicación Excel AlgoLab.xlsm
• Clases de intercambio
  • Comparación de clasificación de intercambio
• Clases de inserción
• Ordenar por selección
• Combinar clasificaciones
• Ordenar por distribución
• Clasificación híbrida