Richard Hamming: Capítulo 17. Filtros digitales - IV

"El objetivo de este curso es prepararte para tu futuro técnico".

Hola Habr ¿Recuerdas el increíble artículo "Tú y tu trabajo" (+219, 2442 marcadores, 393k lecturas)?

Entonces, Hamming (sí, sí, los códigos de Hamming que se autoverifican y corrigen a sí mismos) tiene un libro completo escrito basado en sus conferencias. Lo estamos traduciendo, porque el hombre está hablando de negocios.

Este libro no es solo sobre TI, es un libro sobre el estilo de pensamiento de personas increíblemente geniales. “Esto no es solo una carga de pensamiento positivo; describe condiciones que aumentan las posibilidades de hacer un gran trabajo ".

Ya hemos traducido 24 (de 30) capítulos. Y estamos trabajando en una edición en papel.

Capítulo 17. Filtros digitales - IV

(Gracias por la traducción, Andrei Pakhomov, quien respondió a mi llamada en el "capítulo anterior".) ¿Quién quiere ayudar con la traducción, el diseño y la publicación del libro? Escriba en un correo electrónico personal o magisterludi2016@yandex.ru

Y ahora pasamos a filtros recursivos, que tienen la siguiente forma:



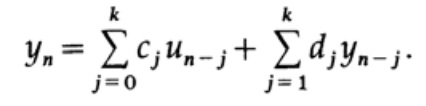
Esta fórmula muestra que tenemos valores solo en un lado del enésimo valor actual. Utilizamos los valores anteriores de la señal y su valor en el momento actual un, así como los valores anteriores obtenidos a la salida del filtro.
Este enfoque clásico es el resultado del hecho de que a menudo procesamos la señal en tiempo real y no tenemos acceso a valores de señal futuros.

Recordando lo básico, veremos que si tuviéramos "valores futuros", probablemente el pronóstico bidireccional sería mucho más preciso. Luego, para calcular yn, nos encontraríamos con un sistema que resolvería instantáneamente ecuaciones lineales, eso está bien en la era de la informática barata. Dejaremos de lado esta observación, hoy a menudo registramos la señal en cinta u otros medios, y luego procesamos los datos en el laboratorio, y por lo tanto tenemos valores futuros para algún momento. Por ejemplo, usar un filtro digital recursivo en el procesamiento de imágenes sería una tontería porque no usa parte de la información relevante disponible.

El siguiente aspecto al que debe prestar atención cuando usa el valor de salida anterior como la siguiente entrada es la presencia de retroalimentación, y esto automáticamente plantea el problema de la estabilidad. Esta es una condición que debemos monitorear constantemente durante el diseño de filtros recursivos. Esto limita lo que podemos hacer. En este caso, la estabilidad significa que el efecto de las condiciones iniciales no comenzará a prevalecer en el resultado final.

Cuando trabajamos con un sistema lineal, vimos que no importa qué frecuencia apliquemos a la entrada del filtro cuando está estacionario, solo esta frecuencia aparece en la salida del filtro, aunque la fase de la señal de salida se puede cambiar en relación con la fase de la señal original. Sin embargo, en el estado de transición, pueden aparecer otras frecuencias que surgen de la solución de una ecuación diferencial homogénea. Un filtro recursivo no es más que una solución de una ecuación diferencial con coeficientes constantes para términos de la ONU que forman una función forzada.

Por lo tanto, para un estado estacionario (ignorando los transitorios), suponemos que



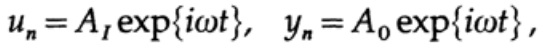
(donde A puede ser números complejos para tener en cuenta el cambio de fase), y esto lleva a la solución de la relación A0 / A1 para encontrar la función de transferencia:



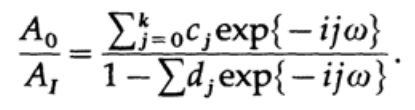
Esta expresión es una función racional de la variable compleja exp {iωt} = z, en contraste con el filtro no recursivo previamente considerado, donde la característica de transferencia era un polinomio en z. Se desarrolla la parte teórica de la representación de la función en forma de expansión en una serie de Fourier; pero hasta ahora no existe una teoría sobre la representación de funciones como las relaciones de dos series de Fourier (creo que no hay razones por las que tal teoría no exista). Por lo tanto, en este momento, los métodos de diseño no son sistemáticos (lo que hizo Kaiser para el diseño de filtros no recursivos), sino que son un conjunto de trucos.

Por lo tanto, tenemos un filtro Butterworth, dos tipos de filtros Chebyshev (dependiendo de la presencia de la misma ondulación en las bandas de paso y supresión) y un filtro elíptico (que se llama así debido al uso de funciones elípticas), que tiene la misma ondulación en ambas bandas.



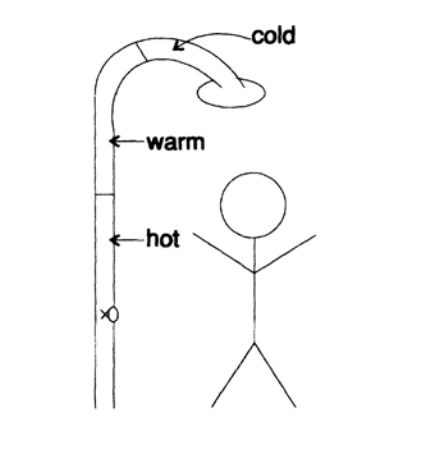Figura 17.1

Solo tocaré el tema de los comentarios. Para aclarar el problema de los comentarios, te contaré una historia sobre mí. Érase una vez, participé en una serie de seis programas de televisión de media hora en computadoras e informática. La filmación tuvo lugar principalmente en San Francisco. A menudo me quedaba allí y tenía la costumbre de quedarme en la misma habitación en el mismo hotel: es genial conocer la habitación con todos los detalles cuando ya es tarde en la noche y estás cansado o cuando tienes que levantarte en medio de la noche, de ahí el deseo de permanecer en el mismo la habitacion.

Es genial que el plomero haya conectado la ducha a tuberías grandes (Figura 17.I). Como resultado, en la mañana, cuando comencé a ducharme, el agua estaba demasiado fría, giré la llave del grifo con agua tibia más, aún demasiado fría y más, aún demasiado fría y aún más, y finalmente, cuando el agua alcanzó la temperatura correcta Me quedé Por supuesto, el agua se calentó más y más cuando salió el agua que previamente había entrado en las tuberías, y tuve que saltar de la ducha e intentar nuevamente encontrar una posición adecuada para el mango del grifo de agua caliente. La demora en el suministro de agua caliente me causó molestias. A pesar de la rica experiencia, me encontré en una situación clásica de inestabilidad. Puedes ver esta situación desde uno de los dos lados: o mi respuesta fue demasiado fuerte (fui muy grosero en mis acciones) o la detección de la señal fue demasiado tarde (fui demasiado apresurado para ajustar el grifo). ¡El mismo efecto duradero! Nunca antes tuve que lidiar con largas demoras, así que todos los días mi mañana comenzó con inconvenientes. En este ejemplo ilustrativo, puede observar la esencia misma de la inestabilidad.

Aquí no profundizaré en el diseño de filtros recursivos, solo noto que durante la lucha con fórmulas correctivas para la solución numérica de ecuaciones diferenciales ordinarias, desarrollé independientemente una teoría.

El corrector en el método predictor-corrector tiene la forma



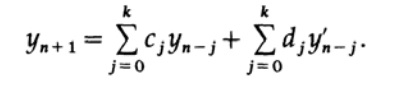
Vemos que ahora los coeficientes uj del filtro recursivo son las derivadas yn 'de la salida del filtro, que se toman de la ecuación diferencial. Los filtros no recursivos convencionales no tienen un ciclo de retroalimentación: los valores calculados de yn no aparecen más adelante en el lado derecho de la expresión. En ecuaciones diferenciales, aparecen tanto en el ciclo de retroalimentación como en sus derivados, formando así otro ciclo de retroalimentación, generalmente no lineal. Por lo tanto, la estabilidad en el campo de la resolución de ecuaciones diferenciales es un tema más complicado que en el campo de los filtros recursivos.

Dichos filtros recursivos a menudo se denominan "filtros con una respuesta de impulso infinita" (filtros IIR), porque una sola perturbación se repetirá a través del bucle de retroalimentación, que decaerá exponencialmente, y solo si el filtro es estable. No sería yo mismo si no me hubiera preguntado si todos los filtros recursivos deberían tener esta propiedad. Pronto encontré el ejemplo opuesto. En verdad, este no es el tipo de filtro que generalmente diseñará, pero este ejemplo muestra que esta afirmación es superficial. Si se pregunta si todo lo que dice es verdad, se sorprenderá de cuántas cosas resultan ser falsas, ¡incluso en áreas bien diseñadas!

En el Capítulo 26, abordaré la cuestión de trabajar con expertos. Ahora verá un ejemplo de lo que sucede con demasiada frecuencia. A los expertos se les dijo algo en el aula cuando todavía eran estudiantes, y no hicieron preguntas, simplemente lo tomaron como un hecho. Y reproducen constantemente este hecho aceptado sin siquiera tratar de verificar si es cierto o no, especialmente en relación con el problema que están tratando de resolver en este momento.

Déjame contarte otra historia ahora. Una señora del departamento de matemáticas de los Laboratorios Labs Bella estaba bailando un baile cuadrado con uno de los físicos en una fiesta de fin de semana, y el lunes por la mañana, en el pasillo, me mencionó un problema que estaba teniendo. Midió el número de pulsos en un experimento radiactivo en cada uno de los 256 niveles de energía que recuerdo. Esto se llama espectro del proceso. Su problema era obtener una derivada de los datos.

Entonces, usted sabe que (a) el número de pulsos de cierto nivel de energía formará una curva con discontinuidades, y (b) diferenciarla para obtener un coeficiente angular local no es una tarea fácil en sí misma. Cuanto más pensaba en su nota al azar, más sentía que necesitaba un buen ayudante, es decir, ¡yo! Lo encontré en el directorio telefónico de los Laboratorios Bell y le expliqué mi interés y cómo lo conocí. Inmediatamente quiso venir a mi oficina, pero yo era terca e insistí en reunirme en su laboratorio. Trató de ofrecer su oficina, pero todavía insistí en su laboratorio. Por qué Para evaluar sus habilidades y decidir si su problema vale mi tiempo y esfuerzo, ya que prometía ser un hueso duro de roer. Pasó la prueba con brillantez por el laboratorio: quedó claro que era un experimentador muy competente.

Estaba casi al límite de lo que podía hacer: se recopilaron datos durante una semana y muchas fuentes ocultaron la fuente de radiación. No parecía que pudieras hacer nada más para recopilar datos más precisos. Además, pronto me convencí, a pesar del hecho de que conocía pocos detalles, de que su experimento era importante tanto para la física como para los Laboratorios Bell. Entonces, asumí esta tarea. Moraleja: hasta cierto punto, puede elegir y trabajar en aquellas tareas que considere importantes.

Obviamente, este era un problema de suavizado, y Kaiser, de hecho, me acaba de entrenar, entonces, ¿qué podría ser mejor que llevar el experimentador a Kaiser y pedirle a Kaiser que diseñe un filtro diferenciador adecuado? Los problemas comenzaron de inmediato. Kaiser siempre pensó en la señal como una función del tiempo, y en el área bajo la curva como energía, ¡y en este caso la energía era una variable independiente! En este punto, el problema con Kaiser se repitió hasta que le dije directamente: "Bueno, su energía es el tiempo y sus medidas, impulsos, este voltaje". Solo después de eso, Kaiser pudo resolver el problema.

La maldición de los expertos radica en su comprensión limitada de lo que pueden hacer. Te mencioné que Kaiser es una persona muy capaz, pero su experiencia, como sucede a menudo con los expertos, limitó su visión. ¿Puedes, a su vez, hacerlo mejor? Espero que estas historias te ayuden a evitar esta trampa.

Como noté anteriormente, generalmente el espectro de la señal útil está en la parte inferior de la banda de Nyquist, y el espectro de ruido se distribuye por toda la banda de Nyquist, por lo que tuvimos que encontrar la frecuencia de corte entre la señal útil del físico y el ruido blanco plano. ¿Cómo encontrarla? Al principio, probé un modelo teórico del experimento desde la cabeza del físico que estaba en su cabeza: eran muchas líneas espectrales estrechas en forma de funciones gaussianas en la parte superior de una función gaussiana amplia (dudaba que fuera una distribución de Cauchy, pero no discutí con ella, ya que la diferencia sería muy pequeño, dada la naturaleza de los datos que teníamos). Entonces, simulamos esta distribución, y él preparó una cierta cantidad de datos sintéticos correspondientes a este modelo. Un análisis espectral rápido de la señal a través de la transformada rápida de Fourier mostró que la señal se encuentra en el 1/20 inferior de la banda Nyquist. ¡Además, procesamos sus datos experimentales de la misma manera y obtuvimos la misma ubicación de frecuencia de corte! Que suerte (Quizás la suerte debería atribuirse a la habilidad del experimentador). Érase una vez, la teoría y la práctica se unieron! Resultó que pudimos filtrar el 95% del ruido. Finalmente, Kaiser escribió un programa para él que sintetizó un filtro para una frecuencia de corte dada, que fue establecido por el experimentador.

El programa (1) calculó un filtro diferenciador adecuado, (2) escribió un programa para calcular la salida suavizada y luego (3) procesó los datos con este filtro sin ninguna intervención del físico.

Más tarde, atrapé a un físico ajustando la frecuencia de corte para diferentes partes de los datos del nivel de energía obtenidos en una serie de mediciones y me vi obligado a recordarle que hay ciertos "grados de libertad" y que lo que hace no es un procesamiento de datos honesto. Se volvió mucho más problemático cuando las cosas iban bien, para persuadirlo de aprovechar al máximo sus datos (que era muy costoso de obtener): debería trabajar con las raíces cuadradas de sus impulsos, ya que tenían la misma variación. Finalmente, entendió esto y lo hizo. Él y Kaiser escribieron un trabajo clásico en esta área que abrió la puerta a nuevas cosas que podrían hacerse.

Mi contribucion Principalmente, primero identifique el problema, luego reúna a las personas adecuadas, luego observe a Kaiser para confrontarlo con el hecho de que el filtrado es necesario no solo para las señales como funciones del tiempo, y finalmente recordarles lo que sabían de las estadísticas (o deberían haberlo hecho) saber, pero tal vez no lo sabían).

Sobre la base de la mía, me parece que la necesidad de ese papel aumenta a medida que las personas se vuelven cada vez más expertos en áreas de conocimiento cada vez más estrechas. Alguien necesita mantener un horizonte amplio y asegurarse de que las cosas se hagan honestamente. Creo que llegué a este papel después de una educación muy larga bajo el liderazgo de John Tukey, además de una buena base en forma de una herramienta universal de la Ciencia llamada Matemáticas. Hablaré sobre la naturaleza de las Matemáticas en el Capítulo 23 .

La mayor parte del procesamiento de la señal proviene de las señales a lo largo del tiempo. Al mismo tiempo, la mayoría de los filtros digitales están diseñados para estudios pequeños y altamente especializados que no están necesariamente asociados con las señales a lo largo del tiempo. Aquí te pediré que tengas cuidado en el futuro. Suponga que tiene un negocio en la cima y está interesado en datos que muestren costos laborales anteriores para el equipo. Serán datos ruidosos, pero aún así quiere comprender, en el sentido habitual, lo que sucede en la organización, qué procesos a largo plazo se están llevando a cabo, aquellos que son tan lentos que las personas los comprenderán cuando ya sucedan, pero no obstante entiendan captura, que es fundamentalmente importante si quieres ser un buen gerente. Necesitará un filtro digital para suavizar los datos y ver indicios de la tendencia, si existe. No desea encontrar una tendencia que no existe, pero si existe, realmente desea saber qué era antes para predecir qué es probable que sea en el futuro cercano. De hecho, deseará ver cambios en la pendiente de la tendencia, si los datos le permiten verla. Algunas señales, como la potencia de fuego en relación con el desplazamiento de la nave, no están vinculadas al tiempo, pero pueden decirle mucho sobre el estado actual de la flota. Por supuesto, puedes estudiar esta relación en función del tiempo.

En la parte superior de su carrera, podrá utilizar una variedad de filtros digitales de bajo nivel para señales en función del tiempo, y no solo para administrar mejor las cosas. Por lo tanto, sostengo que probablemente sintetice muchos más filtros digitales para cosas no estándar que para reducir los datos de radar y aplicaciones clásicas similares. Por lo general, es en nuevas aplicaciones de conocimiento que puede obtener el mayor rendimiento.

Permítanme expresar algunas inquietudes con respecto al uso incorrecto de herramientas inteligentes; con más detalle hablaré sobre temas cercanos a las estadísticas en el Capítulo 27 . El análisis de expansión de Fourier supone la linealidad del modelo subyacente. Puede usarlo para casos ligeramente no lineales, pero la mayoría de las veces, el análisis hábilmente realizado por la expansión de Fourier falla, ya que el fenómeno investigado es de naturaleza demasiado no lineal. Vi cómo se desperdiciaron millones de dólares cuando era bastante obvio para los extraños que las no linealidades distorsionarían todo el análisis lineal realizado por aproximación por series de Fourier. Cuando señalaron esto, su respuesta fue que no sabían qué otro enfoque podría adoptarse, ¡así que continuaron haciendo lo incorrecto! Y no estoy exagerando aquí.



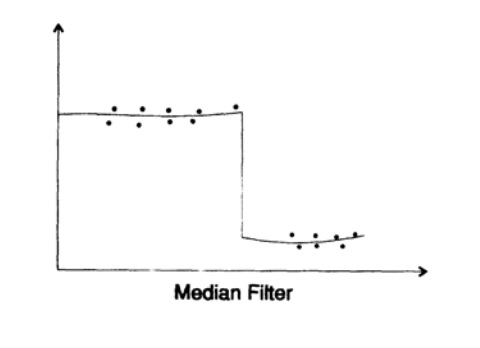Figura 17.2

¿Qué pasa con los filtros no lineales? Las posibilidades aquí son infinitas y dependen, por supuesto, del problema con el que está lidiando. Trataré solo con uno de ellos, el filtro mediano.Considera la salida del filtro mediano para un conjunto de datos específico. Veamos cómo funciona en la práctica. En primer lugar, observamos que busca suavizar cualquier ruido local, pero ¿cómo se comportará el filtro en el punto de ruptura (Fig. 17.2)?

Con un número impar de miembros en el filtro mediano, verá que la salida del filtro permanece en el nivel superior hasta que más de la mitad de los puntos en la entrada del filtro estén en el nivel inferior, después de lo cual la salida del filtro "salta" hacia abajo. ¡Seguirá los descansos lo suficientemente bien y no intentará suavizarlos por completo! En algunos casos, este es exactamente el tipo de filtro que le conviene: el ruido local se suaviza, mientras que los cambios repentinos en el estado del sistema en estudio no se perderán.

Repito que el análisis de la serie de Fourier es lineal, mientras que hay una gran cantidad de filtros no lineales, pero la teoría no está bien desarrollada para otra cosa que no sea un filtro mediano. El filtro de Kalman es otro ejemplo del uso de un filtro parcialmente no lineal, la parte no lineal es el "ajuste" independiente del filtro a la señal.

Finalmente, aquí hay otra observación fundamental que hice al estudiar los filtros digitales. Un día, mientras estudiaba un libro sobre integrales de Fourier, encontré un teorema que afirmaba que la variación de una función multiplicada por la variación de su transformación debería ser mayor que una cierta constante. Me pregunté: "¿Qué es sino el famoso principio de incertidumbre de la mecánica cuántica"? Sí, toda teoría lineal debería tener un principio de incertidumbre que vincule las variables conjugadas. Tan pronto como adopte el enfoque lineal, y el CM afirma la aditividad absoluta de los estados propios, debe descubrir el principio de incertidumbre. La invariancia lineal del tiempo conduce automáticamente a las funciones propias e ^ iω (t). Inmediatamente conducen a la serie de Fourier y, a su vez, tienen el principio de incertidumbre.Es como si usara lentes de color azul. Lo que sea que mires, ¡debería tener un tinte azulado!

Por lo tanto, no está realmente seguro de si el famoso principio de incertidumbre CM existe o no; tal vez esto sea solo el efecto de la linealidad implícita del sistema.

¡Pocas personas quieren creer que lo que vemos depende de qué lado abordemos el problema! Muy a menudo vemos lo que queremos ver, y es por eso que debe usar un enfoque científico en todas partes, dudando de sus propias creencias.
Para demostrar esto claramente, repetiré la historia de Eddington sobre los pescadores. Pescaban en la red, y cuando examinaron el tamaño de los peces capturados en la red, decidieron que había un tamaño mínimo de peces en el mar.

En conclusión, si no duda de las reglas adoptadas, de vez en cuando, lo más probable es que no se convierta en líder en ningún campo, por otro lado, si duda de todo, quedará paralizado y no hará nada. . Cuándo dudar, cuándo aprender los conceptos básicos, cuándo pensar por sí mismo y cuándo continuar y tomar las cosas como son, es una cuestión de estilo de pensamiento, y no puedo dar una fórmula simple para resolver este problema. Debes aprender de tu propia experiencia. Las grandes ganancias generalmente vienen después de cambios significativos en los supuestos subyacentes en los que se basa el área. El estado de nuestro conocimiento determina el equilibrio entre varios aspectos de la investigación. Parece que cuando eres joven, la intuición y la comprensión tienen más tiempo para pagar, pero cuando eres viejo,queda menos tiempo para esto y probablemente debería concentrarse en lo que ya está a su alcance.

Continuará ...

¿Quién quiere ayuda con la traducción, diseño y publicación de un libro - escritura en un magisterludi2016@yandex.ru personal o electrónico

Por cierto, hemos puesto en marcha una traducción de otro más fresco libro - «del sueño de la máquina: La historia de la revolución del ordenador" )