En esta serie de artículos, se familiarizará con los principios básicos de la programación funcional y comprenderá lo que significa "pensar funcionalmente" y cómo este enfoque difiere de la programación orientada a objetos o imperativa.

Ahora que ha visto algunas de las razones por las que debería usar F #, en el artículo " Bucear en F #. Una guía para desarrolladores de C # ”, dé un paso atrás y analice los conceptos básicos de la programación funcional. ¿Qué significa realmente "programación funcional", y cómo difiere este enfoque de la programación orientada a objetos o imperativa?
Cambio de mentalidad (Introducción)
Es importante comprender que la programación funcional no es solo un estilo de programación separado. Esta es una forma de pensar completamente diferente en la programación, que difiere del enfoque "tradicional" tan significativamente como la OOP actual (en el estilo Smalltalk) difiere de un lenguaje imperativo tradicional como C.
F # le permite usar estilos de codificación no funcionales, y esto tienta al programador a preservar sus hábitos existentes. Puede programar en F # la forma en que está acostumbrado, sin cambiar radicalmente la visión del mundo y sin siquiera saber lo que se está perdiendo. Sin embargo, para sacar el máximo provecho de F #, y también para aprender a programar con confianza en un estilo funcional en general, es muy importante aprender a pensar de una manera funcional y no imperativa.
El propósito de esta serie de artículos es ayudar al lector a comprender los antecedentes de la programación funcional y cambiar su forma de pensar.
Esta será una serie bastante abstracta, aunque usaré muchos ejemplos de códigos cortos para demostrar algunos puntos. Cubriremos los siguientes temas:
- Funciones matematicas . El primer artículo presenta los conceptos matemáticos que subyacen a los lenguajes funcionales y los beneficios que aporta este enfoque.
- Funciones y valores . A continuación se presentan funciones y valores, se explica cómo los "valores" difieren de las variables y cuáles son las similitudes entre funciones y valores simples.
- Tipos Luego pasamos a los tipos principales que funcionan con funciones: tipos primitivos como string e int, tipo de unidad, tipos funcionales y tipos genéricos.
- Funciones con varios parámetros . Explicaré más detalladamente los conceptos de "curry" y "aplicación parcial". En este lugar, el cerebro de alguien se lastimará, especialmente si estos cerebros solo tienen un pasado imperativo.
- Definición de funciones . Luego, se dedicarán varias publicaciones a muchas formas diferentes de definir y combinar funciones.
- Firmas de funciones . La siguiente es una publicación importante sobre el valor crítico de las firmas de funciones, lo que significan y cómo usar las firmas para comprender el contenido de las funciones.
- Organización de funciones . Cuando queda claro cómo crear funciones, surge la pregunta: ¿cómo puede organizarlas para hacerlas accesibles al resto del código?
Funciones matemáticas
La programación funcional está inspirada en las matemáticas. Las funciones matemáticas tienen una serie de características muy agradables que los lenguajes funcionales intentan implementar.
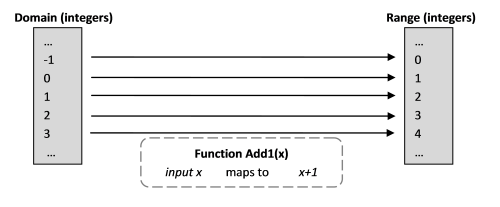
Comencemos con una función matemática que agrega 1 a un número.
Add1(x) = x+1
¿Qué significa realmente esta expresión? Se ve bastante simple. Significa que existe una operación que toma un número y le agrega 1.
Agregue alguna terminología:
- El conjunto de valores de función de entrada válidos se denomina dominio (ámbito). En este ejemplo, podrían ser muchos números reales, pero simplificaremos la vida y nos limitaremos aquí a números enteros.
- El conjunto de resultados posibles de la función (rango de valores) se llama rango (técnicamente, la imagen del codominio ). En este caso, también hay muchos enteros.
- Una función se llama mapeo (en el mapa original) del dominio al rango. (Es decir, del alcance al alcance).
Así es como se verá esta definición en F #.
let add1 x = x + 1
Si lo ingresa en F # Interactive (no olvide los puntos y comas dobles), puede ver el resultado (la "firma" de la función):
val add1 : int -> int
Considere la conclusión en detalle:
- El significado general es que la función
add1 compara enteros (del dominio de definición) con enteros (del rango de valores). - "
add1 " se define como "val", abreviatura de "valor". Hm? que significa Discutiremos los significados un poco más tarde. - La notación de flecha "->" se utiliza para mostrar el dominio y el rango. En este caso, el dominio es del tipo 'int', como el rango.
Tenga en cuenta que el tipo no se especificó explícitamente, pero el compilador de F # decidió que la función funciona con ints. (¿Se puede cambiar esto? Sí, y pronto lo veremos).
Propiedades clave de las funciones matemáticas.
Las funciones matemáticas tienen una serie de propiedades que las distinguen mucho de las funciones que se utilizan en la programación de procedimientos.
- Una función siempre tiene el mismo resultado para el mismo valor de entrada.
- La función no tiene efectos secundarios.
Estas propiedades proporcionan una serie de ventajas notables que los lenguajes de programación funcionales intentan obtener en su diseño tanto como sea posible. Consideraremos cada uno de ellos a su vez.
Las funciones matemáticas siempre devuelven el mismo resultado a un valor dado
En la programación imperativa, creemos que las funciones "hacen" algo o "cuentan" algo. Las funciones matemáticas no cuentan nada, son asignaciones puras de entrada a salida. De hecho, otra definición de una función es un conjunto simple de todas las asignaciones. Por ejemplo, es muy crudamente posible definir la función "add1" (en C #) como
int add1(int input) { switch (input) { case 0: return 1; case 1: return 2; case 2: return 3; case 3: return 4; etc ad infinitum } }
Obviamente, es imposible tener un caso para cada número posible, pero el principio es el mismo. Con esta configuración, no se realizan cálculos, solo se realiza una búsqueda.
Funciones matemáticas sin efectos secundarios.
En una función matemática, los valores de entrada y salida son lógicamente dos cosas diferentes, ambas predefinidas. La función no cambia los datos de entrada o salida y simplemente asigna el valor de entrada predefinido del área de definición al valor de salida predefinido en el área de valor.
En otras palabras, el cálculo de una función no puede tener ningún efecto sobre los datos de entrada o cualquier otra cosa de este tipo . Debe recordarse que el cálculo de una función realmente no cuenta ni manipula nada, es solo una búsqueda sobrevalorada.
Esta "inmutabilidad" de los valores es muy sutil, pero al mismo tiempo es algo muy importante. Cuando hago matemáticas, no espero que los números cambien a medida que se agregan. Por ejemplo, si tengo:
x = 5 y = x+1
No espero que x cambie cuando agregue 1. Espero obtener un número diferente ( y ), y x debería permanecer intacta. En el mundo de las matemáticas, los enteros ya existen en un conjunto inmutable, y la función add1 simplemente determina la relación entre ellos.
El poder de la función pura.
Ese tipo de funciones que tienen resultados repetibles y no tienen efectos secundarios se denominan "funciones puras", y puede hacer algunas cosas interesantes con ellas:
- Son fáciles de paralelizar. Digamos que podríamos tomar números enteros en el rango de 1 a 1000 y distribuirlos a 1000 procesadores diferentes, después de lo cual le indicamos a cada CPU que ejecute "
add1 " en el número correspondiente, al tiempo que nos aseguramos de que no haya necesidad de interacción entre ellos. Sin cerraduras, sin mutexes, sin semáforos, etc. - Puede usar funciones con pereza, calculando cuando sea necesario para la lógica del programa. Puede estar seguro de que la respuesta será exactamente la misma, independientemente de si los cálculos se realizan ahora o más tarde.
- Solo puede realizar cálculos de funciones para una entrada específica y luego almacenar en caché el resultado, porque se sabe que estos valores de entrada darán la misma salida.
- Si hay muchas funciones puras, se pueden calcular en cualquier orden. Nuevamente, esto no puede afectar el resultado final.
En consecuencia, si es posible crear funciones puras en un lenguaje de programación, puede recibir inmediatamente muchos trucos poderosos. Y, sin duda, todo esto se puede hacer en F #:
- Un ejemplo de computación paralela fue en la serie "¿Por qué usar F #?" .
- El cálculo de la función diferida se discutirá en la serie Optimización .
- Los resultados de la función de almacenamiento en caché se denominan memorización y también se analizarán en la serie Optimización .
- La ausencia de la necesidad de rastrear el orden de ejecución hace que la programación paralela sea mucho más fácil y elimina la necesidad de errores causados por cambiar el orden de las funciones o la refactorización.
Propiedades "inútiles" de funciones matemáticas
Las funciones matemáticas también tienen algunas propiedades que parecen no ser muy útiles al programar.
- Los valores de entrada y salida son inmutables.
- Las funciones siempre tienen una entrada y una salida.
Estas propiedades se reflejan en el diseño de lenguajes de programación funcionales. Vale la pena considerarlos por separado.
Los valores de entrada y salida son inmutables.
Los valores inmutables en teoría parecen una buena idea, pero ¿cómo se puede hacer realmente cualquier trabajo si no hay forma de asignar una variable de la manera tradicional?
Les puedo asegurar que este no es un problema tan grande como pueden imaginar. En esta serie de artículos, quedará claro cómo funciona esto en la práctica.
Las funciones matemáticas siempre tienen una entrada y una salida.
Como se puede ver en los diagramas, para una función matemática siempre hay solo una entrada y solo una salida. Esto también es cierto para los lenguajes de programación funcionales, aunque puede no ser obvio cuando se usa por primera vez.
Esto parece un gran inconveniente. ¿Cómo puedo hacer algo útil sin funciones con dos (o más) parámetros?
Resulta que hay una manera de hacer esto, y lo que es más, es completamente transparente en F #. Se llama "curry", y merece una publicación separada, que aparecerá en un futuro próximo.
De hecho, más tarde quedará claro que estas dos propiedades "inútiles" se volverán increíblemente valiosas y serán la parte clave que hace que la programación funcional sea tan poderosa.
Recursos Adicionales
Hay muchos tutoriales para F #, incluidos los materiales para aquellos que vienen con experiencia en C # o Java. Los siguientes enlaces pueden ser útiles a medida que profundiza en F #:
También se describen varias otras formas de comenzar a aprender F # .
Finalmente, la comunidad F # es muy amigable para principiantes. Hay un chat muy activo en Slack, respaldado por la F # Software Foundation, con salas para principiantes a las que puedes unirte libremente . ¡Recomendamos encarecidamente que haga esto!
¡No te olvides de visitar el sitio de la comunidad de habla rusa F # ! Si tiene alguna pregunta sobre el aprendizaje de un idioma, estaremos encantados de discutirlo en las salas de chat:
Sobre autores de traducción
Traducido por @kleidemos
 La traducción y los cambios editoriales fueron realizados por los esfuerzos de la comunidad de desarrolladores de F # de habla rusa . También agradecemos a @schvepsss y @shwars por preparar este artículo para su publicación.
La traducción y los cambios editoriales fueron realizados por los esfuerzos de la comunidad de desarrolladores de F # de habla rusa . También agradecemos a @schvepsss y @shwars por preparar este artículo para su publicación.