Mapeo normal

Todas las escenas que utilizamos están formadas por polígonos, que a su vez están formados por cientos, miles de triángulos absolutamente planos. Ya hemos logrado aumentar ligeramente el realismo de las escenas debido a detalles adicionales que proporcionan la aplicación de texturas bidimensionales en estos triángulos planos. El texturizado ayuda a ocultar el hecho de que todos los objetos en la escena son solo una colección de muchos triángulos pequeños. Una gran técnica, pero sus posibilidades no son ilimitadas: al acercarse a cualquier superficie, todo queda claro que consiste en superficies planas. La mayoría de los objetos reales no son completamente planos y muestran muchos detalles en relieve.


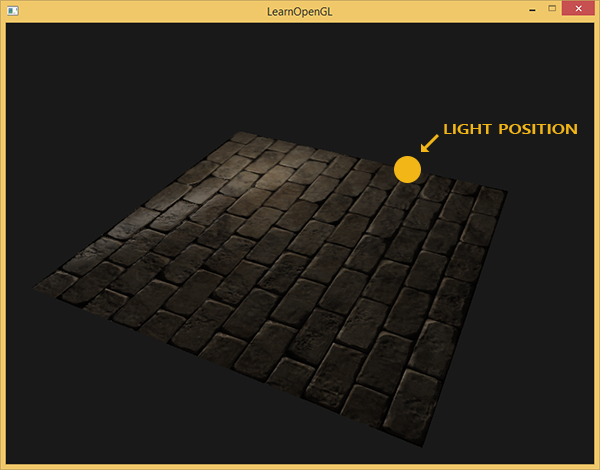
Por ejemplo, toma ladrillos. Su superficie es muy rugosa y, obviamente, no está representada por un plano: en ella hay huecos con cemento y muchos pequeños detalles, como agujeros y grietas. Si analizamos una escena con imitación de ladrillo en presencia de iluminación, entonces la ilusión del relieve superficial se destruye muy fácilmente. El siguiente es un ejemplo de tal escena que contiene un plano con una textura de mampostería y una fuente de luz de un punto:


Como puede ver, la iluminación no tiene en cuenta los detalles de relieve asumidos para esta superficie: todas las pequeñas grietas y cavidades con cemento también son indistinguibles del resto de la superficie. Se podría usar un mapa de brillo especular para limitar la iluminación de ciertos detalles que se encuentran en los huecos de la superficie. Pero esto parece más un truco sucio que una solución de trabajo. Lo que necesitamos es una forma de proporcionar a las ecuaciones de iluminación datos sobre el microrelieve de la superficie.
En el contexto de las ecuaciones de iluminación que conocemos, considere esta pregunta: ¿bajo qué condiciones se iluminará la superficie como perfectamente plana? La respuesta está relacionada con lo normal a la superficie. Desde el punto de vista del algoritmo de iluminación, la información sobre la forma de la superficie se transmite solo a través del vector normal. Dado que el vector normal es constante en todas partes en la superficie presentada anteriormente, la iluminación también sale uniforme, correspondiente al plano. Pero, ¿qué pasa si pasamos al algoritmo de iluminación no la única constante normal para todos los fragmentos que pertenecen al objeto, sino la única normal para cada fragmento? Por lo tanto, el vector normal cambiará ligeramente según la topografía de la superficie, lo que creará una ilusión más convincente de la complejidad de la superficie:


Mediante el uso de normales fragmentariamente diferentes, el algoritmo de iluminación considerará que la superficie está compuesta de muchos planos microscópicos perpendiculares a su vector normal. Como resultado, esto agregará significativamente textura al objeto. La técnica de aplicar normales únicos a un fragmento y no a toda la superficie: esto es el mapeo normal o el mapeo de relieve . Aplicado a una escena ya familiar:


Puede ver el impresionante aumento en la complejidad visual debido al costo muy modesto del rendimiento. Dado que todos los cambios en el modelo de iluminación solo están en el suministro de una normal única en cada fragmento, entonces no se cambian las fórmulas de cálculo. Solo en la entrada, en lugar de la normal interpolada, la normal para el fragmento actual sale a la superficie. Las mismas ecuaciones de iluminación hacen el resto del trabajo para crear la ilusión de alivio.

Mapeo normal

Entonces, resulta que necesitamos proporcionar al algoritmo de iluminación normales que sean exclusivas de cada fragmento. Usaremos el método ya conocido en texturas de reflexión difusa y especular y usaremos la textura 2D habitual para almacenar datos normales en cada punto de la superficie. No se sorprenda, las texturas también son excelentes para almacenar vectores normales. Luego solo tenemos que seleccionar la textura, restaurar el vector normal y realizar cálculos de iluminación.

A primera vista, puede que no esté muy claro cómo guardar los datos vectoriales en una textura regular, que generalmente se usa para almacenar información de color. Pero piense por un segundo: la tríada de color RGB es esencialmente un vector tridimensional. De manera similar, puede guardar los componentes del vector normal XYZ en los componentes de color correspondientes. Los valores de los componentes del vector normal se encuentran en el intervalo [-1, 1] y, por lo tanto, requieren una conversión adicional al intervalo [0, 1]:

vec3 rgb_normal = normal * 0.5 + 0.5; //   [-1,1]  [0,1] 

Tal reducción del vector normal al espacio de los componentes de color RGB nos permitirá guardar el vector normal en la textura, obtenida sobre la base del relieve real del objeto modelado y único para cada fragmento. Un ejemplo de tal textura - mapas normales - para el mismo ladrillo:


Es interesante observar el tinte azul de este mapa normal (casi todos los mapas normales tienen un tinte similar). Esto sucede porque todas las normales están orientadas aproximadamente a lo largo del eje oZ, que está representado por la coordenada triple (0, 0, 1), es decir. en forma de tríada de colores: azul puro. Pequeños cambios en el tono son consecuencia de la desviación de las normales del semi-eje positivo oZ en algunas áreas, que corresponde a terreno irregular. Entonces, puede ver que en los bordes superiores de cada ladrillo, la textura adquiere un tono verde. Y esto es lógico: en las caras superiores del ladrillo, las normales deben orientarse más hacia el eje oY (0, 1, 0), que corresponde al verde.

Para la escena de prueba, tome un plano orientado hacia el semieje positivo oZ y use el siguiente mapa difuso y el mapa normal para él.

Tenga en cuenta que el mapa normal en el enlace y en la imagen de arriba son diferentes. En el artículo, el autor mencionó casualmente las razones de las diferencias, limitándose a aconsejar que los mapas normales se conviertan para que el componente verde indique "abajo" en lugar de "arriba" en el sistema local del plano de textura.
Si observa con más detalle, entonces dos factores interactúan aquí:

• La diferencia es cómo se abordan los texels en la memoria del cliente y en la memoria de textura OpenGL
• La presencia de dos notaciones para mapas normales. Convencionalmente, dos campamentos: estilo DirectX y estilo OpenGL

En cuanto a las anotaciones de mapas normales, históricamente familiares son dos campos: DirectX y OpenGL.

Aparentemente, no son compatibles. Y con un poco de reflexión, puede comprender que DirectX considera que el espacio tangente es para zurdos y OpenGL para diestros. Deslizar el mapa X normal de nuestra aplicación sin ningún cambio dará como resultado una iluminación incorrecta, y no siempre queda claro de inmediato que sea incorrecto. En particular, las protuberancias en el formato OpenGL se convierten en hendiduras para DirectX y viceversa.
En cuanto al direccionamiento: cargar datos de un archivo de textura en la memoria, suponemos que el primer texel es el texel superior izquierdo de la imagen. Para representar datos de textura en la memoria de la aplicación, esto es generalmente cierto. Pero OpenGL usa un sistema de coordenadas de textura diferente: para ello, el primer texel es la esquina inferior izquierda. Para una textura correcta, las imágenes generalmente se voltean a lo largo del eje Y en el código de uno u otro cargador de archivos de imagen. Para Stb_image utilizado en las lecciones, debe agregar una casilla de verificación

 stbi_set_flip_vertically_on_load(1); 

Lo curioso es que dos opciones se muestran correctamente en términos de iluminación: un mapa normal en notación OpenGL con la reflexión Y activada o un mapa normal en notación DirectX con la reflexión Y desactivada. La iluminación en ambos casos funciona correctamente, la diferencia solo permanecerá en el inverso de la textura a lo largo del eje Y.

Nota trans.

Entonces, cargue ambas texturas, enlace a los bloques de textura y renderice el plano preparado, teniendo en cuenta las siguientes modificaciones del código del sombreador de fragmentos:

 uniform sampler2D normalMap; void main() { //         [0,1] normal = texture(normalMap, fs_in.TexCoords).rgb; //      [-1,1] normal = normalize(normal * 2.0 - 1.0); [...] //  ... } 

Aquí aplicamos la transformación inversa del espacio de valores RGB a un vector normal completo y luego simplemente la usamos en el conocido modelo de iluminación Blinn-Fong.

Ahora, si cambia lentamente la posición de la fuente de luz en la escena, puede sentir la ilusión del alivio de la superficie que proporciona el mapa normal:


Pero queda un problema que reduce drásticamente el rango de uso posible de los mapas normales. Como ya se señaló, el tinte azul del mapa normal insinuó que todos los vectores en la textura están orientados en promedio a lo largo del eje positivo oZ. En nuestra escena, esto no creó problemas, porque lo normal a la superficie del avión también estaba alineado con oZ. Sin embargo, ¿qué sucede si cambiamos la posición del plano en la escena para que lo normal esté alineado con el eje positivo oY?


¡La iluminación resultó estar completamente equivocada! Y la razón es simple: las normales del mapa aún devuelven vectores orientados a lo largo del semieje positivo oZ, aunque en este caso deberían orientarse en la dirección del semieje positivo oY de la superficie normal. Al mismo tiempo, el cálculo de la iluminación es como si las normales a la superficie estuvieran ubicadas como si el plano aún estuviera orientado hacia el semieje positivo oZ, lo que da un resultado incorrecto. La siguiente figura muestra más claramente la orientación de las normales leídas del mapa en relación con la superficie:


Se puede ver que las normales están generalmente alineadas a lo largo del semieje positivo oZ, aunque deberían haberse alineado a lo largo de la normal a la superficie que se dirige a lo largo del semieje positivo oY.
Una posible solución sería establecer un mapa normal separado para cada orientación de la superficie en consideración. Para un cubo, se necesitarían seis mapas normales, pero para modelos más complejos, el número de orientaciones posibles puede ser demasiado alto y no adecuado para la implementación.

Existe otro enfoque matemáticamente más complicado, que ofrece calcular la iluminación en un sistema de coordenadas diferente: de modo que los vectores normales siempre coincidan aproximadamente con el medio eje positivo oZ. Otros vectores necesarios para los cálculos de iluminación se convierten a este sistema de coordenadas. Este método permite utilizar un mapa normal para cualquier orientación del objeto. Y este sistema de coordenadas específico se llama espacio tangente o espacio tangente .

Espacio tangente

Cabe señalar que el vector normal en el mapa normal se expresa directamente en el espacio tangente, es decir. en un sistema de coordenadas tal que lo normal siempre se dirige aproximadamente en la dirección del semieje positivo oZ. El espacio tangente se define como un sistema de coordenadas local al plano del triángulo, y cada vector normal se define dentro de este sistema de coordenadas. Puede imaginar este sistema como un sistema de coordenadas local para un mapa normal: todos los vectores en él se dirigen hacia el semieje positivo oZ, independientemente de la orientación final de la superficie. Utilizando matrices de transformación especialmente preparadas, es posible transformar vectores normales de este sistema de coordenadas de tangente local a coordenadas mundiales o de visualización, orientándolos de acuerdo con la posición final de las superficies texturizadas.
Considere el ejemplo anterior con el uso incorrecto del mapeo normal, donde el plano estaba orientado a lo largo del eje positivo oY. Como el mapa de las normales se define en el espacio tangente, una de las opciones de ajuste es calcular la matriz de transición de las normales del espacio tangente a una orientación normal a la superficie. Esto causaría que las normales se alineen a lo largo del eje positivo oY. Una propiedad notable del espacio tangente es el hecho de que al calcular dicha matriz podemos reorientar las normales a cualquier superficie y su orientación.

Dicha matriz se abrevia como TBN , que es la abreviatura del nombre del triple de vectores Tangente , Bitangente y Normal . Necesitamos encontrar estos tres vectores para formar esta matriz de cambio de base. Tal matriz hace la transición de un vector desde el espacio tangente a otro y para su formación son necesarios tres vectores perpendiculares entre sí, cuya orientación corresponde a la orientación del plano del mapa normal. Este es un vector de dirección hacia arriba, hacia la derecha y hacia adelante, un conjunto que nos resulta familiar de la lección sobre la cámara virtual .
Con el vector superior, todo está claro de inmediato: este es nuestro vector normal. Los vectores derecho y directo se llaman tangente y bitangente, respectivamente. La siguiente figura da una idea de su posición relativa en el avión:


El cálculo de la tangente y la bi-tangente no es tan obvio como el cálculo del vector normal. En la figura, puede ver que las direcciones de la tangente y el mapa de tangente de la normalidad están alineados con los ejes que especifican las coordenadas de textura de la superficie. Este hecho es la base para calcular estos dos vectores, que requerirán cierta habilidad con las matemáticas. Mira la foto:


Cambios en las coordenadas de textura a lo largo del borde de un triángulo. $$$E_2$ designado como $$$\ Delta U_2$ y $$$\ Delta V_2$ expresado en las mismas direcciones que los vectores tangentes $$$T$ y bi-tangente $$$B$ . En base a este hecho, puede expresar los bordes de un triángulo $$$E_1$ y $$$E_2$ en forma de una combinación lineal de vectores tangentes y bi-tangentes:

$$

$$E_1 = \ Delta U_1T + \ Delta V_1B$$

$$

$$E_2 = \ Delta U_2T + \ Delta V_2B$$

Transformando en un registro bit a bit obtenemos:

$$

$$(E_ {1x}, E_ {1y}, E_ {1z}) = \ Delta U_1 (T_x, T_y, T_z) + \ Delta V_1 (B_x, B_y, B_z)$$

$$

$$(E_ {2x}, E_ {2y}, E_ {2z}) = \ Delta U_2 (T_x, T_y, T_z) + \ Delta V_2 (B_x, B_y, B_z)$$

$$$E$ se calcula como el vector de la diferencia de dos vectores, y $$$\ Delta U$ y $$$\ Delta V$ como la diferencia en las coordenadas de textura. Queda por encontrar dos incógnitas en dos ecuaciones: la tangente $$$T$ y sesgo $$$B$ . Si recuerda las lecciones de álgebra, sabe que tales condiciones hacen posible resolver el sistema por $$$T$ y para $$$B$ .
La última forma dada de ecuaciones nos permite reescribirla en forma de multiplicación matricial:

$$

$$\ begin {bmatrix} E_ {1x} y E_ {1y} y E_ {1z} \\ E_ {2x} y E_ {2y} y E_ {2z} \ end {bmatrix} = \ begin {bmatrix} \ Delta U_1 & \ Delta V_1 \\ \ Delta U_2 & \ Delta V_2 \ end {bmatrix} \ begin {bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \ end {bmatrix}$$

Intenta hacer una multiplicación matricial en tu mente para asegurarte de que el registro sea correcto. Escribir un sistema en forma de matriz hace que sea mucho más fácil comprender el enfoque para encontrar $$$T$ y $$$B$ . Multiplica ambos lados de la ecuación por el inverso de $$$\ Delta U \ Delta V$ :

$$

$$\ begin {bmatrix} \ Delta U_1 & \ Delta V_1 \\ \ Delta U_2 & \ Delta V_2 \ end {bmatrix} ^ {- 1} \ begin {bmatrix} E_ {1x} & E_ {1y} & E_ {1z } \\ E_ {2x} & E_ {2y} & E_ {2z} \ end {bmatrix} = \ begin {bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \ end {bmatrix}$$

Tenemos una decisión sobre $$$T$ y $$$B$ , que, sin embargo, requiere el cálculo de la matriz inversa de cambios en las coordenadas de textura. No entraremos en detalles sobre el cálculo de matrices inversas: la expresión para la matriz inversa se parece al producto del número inverso al determinante de la matriz original y la matriz adjunta:

$$

$$\ begin {bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z \ end {bmatrix} = \ frac {1} {\ Delta U_1 \ Delta V_2 - \ Delta U_2 \ Delta V_1} \ begin {bmatrix} \ Delta V_2 & - \ Delta V_1 \\ - \ Delta U_2 & \ Delta U_1 \ end {bmatrix} \ begin {bmatrix} E_ {1x} & E_ {1y} & E_ {1z} \\ E_ {2x} & E_ { 2y} & E_ {2z} \ end {bmatrix}$$

Esta expresión es la fórmula para calcular el vector tangente $$$T$ y bi-tangente $$$B$ basado en las coordenadas de las caras del triángulo y las coordenadas de textura correspondientes.
No se preocupe si la esencia de los cálculos matemáticos anteriores se le escapa. Si comprende que obtenemos la tangente y la tangente de sesgo en función de las coordenadas de los vértices del triángulo y sus coordenadas de textura (dado que las coordenadas de textura también pertenecen al espacio de tangente), esto ya es la mitad de la batalla.

Cálculo de tangentes y bitangentes.

En el ejemplo de esta lección, tomamos un plano simple mirando hacia el semieje positivo oZ. Ahora intentaremos implementar el mapeo normal usando el espacio tangente para poder orientar el plano en el ejemplo como queramos sin destruir el efecto de mapeo normal. Usando el cálculo anterior, encontramos manualmente la tangente y la bi-tangente a la superficie bajo consideración.
Suponemos que el plano está compuesto por los siguientes vértices con coordenadas de textura (los vectores 1, 2, 3 y 1, 3, 4 dan dos triángulos):

 //   glm::vec3 pos1(-1.0, 1.0, 0.0); glm::vec3 pos2(-1.0, -1.0, 0.0); glm::vec3 pos3( 1.0, -1.0, 0.0); glm::vec3 pos4( 1.0, 1.0, 0.0); //   glm::vec2 uv1(0.0, 1.0); glm::vec2 uv2(0.0, 0.0); glm::vec2 uv3(1.0, 0.0); glm::vec2 uv4(1.0, 1.0); //   glm::vec3 nm(0.0, 0.0, 1.0); 

Primero, calculamos los vectores que describen las caras del triángulo, así como los deltas de las coordenadas de textura:

 glm::vec3 edge1 = pos2 - pos1; glm::vec3 edge2 = pos3 - pos1; glm::vec2 deltaUV1 = uv2 - uv1; glm::vec2 deltaUV2 = uv3 - uv1; 

Con los datos iniciales necesarios en la mano, podemos comenzar a calcular la tangente y la bi-tangente directamente por las fórmulas de la sección anterior:

 float f = 1.0f / (deltaUV1.x * deltaUV2.y - deltaUV2.x * deltaUV1.y); tangent1.x = f * (deltaUV2.y * edge1.x - deltaUV1.y * edge2.x); tangent1.y = f * (deltaUV2.y * edge1.y - deltaUV1.y * edge2.y); tangent1.z = f * (deltaUV2.y * edge1.z - deltaUV1.y * edge2.z); tangent1 = glm::normalize(tangent1); bitangent1.x = f * (-deltaUV2.x * edge1.x + deltaUV1.x * edge2.x); bitangent1.y = f * (-deltaUV2.x * edge1.y + deltaUV1.x * edge2.y); bitangent1.z = f * (-deltaUV2.x * edge1.z + deltaUV1.x * edge2.z); bitangent1 = glm::normalize(bitangent1); [...] //         

Primero, sacamos el componente fraccional de la expresión final en una variable separada f . Luego, para cada componente de los vectores, realizamos la parte correspondiente de la multiplicación de matrices y multiplicamos por f . Al comparar este código con la fórmula de cálculo final, puede ver que esta es su disposición literal. No olvides normalizar al final, para que los vectores encontrados sean unitarios.

Como el triángulo es una figura plana, es suficiente calcular la tangente y la bi-tangente una vez por triángulo; serán los mismos para todos los vértices. Vale la pena señalar que la mayoría de las implementaciones de trabajar con modelos (como cargadores o generadores de paisajes) utilizan una organización de triángulos, donde comparten vértices con otros triángulos. En tales casos, los desarrolladores generalmente recurren a parámetros promedio en vértices comunes, como vectores normales, tangentes y bi-tangentes, para obtener un resultado más uniforme. Los triángulos que forman nuestro plano también comparten varios vértices, pero dado que ambos se encuentran en el mismo plano, no se requiere promediar. Sin embargo, es útil recordar la presencia de este enfoque en aplicaciones y tareas reales.

Los vectores tangentes y bi-tangentes resultantes deben tener valores (1, 0, 0) y (0, 1, 0), respectivamente. Que junto con el vector normal (0, 0, 1) forman la matriz ortogonal TBN. Si visualiza la base resultante con el plano, obtendrá la siguiente imagen:


Ahora, habiendo calculado los vectores, puede proceder a la implementación completa del mapeo normal.

Mapeo normal en espacio tangente

Primero debe crear una matriz TBN en los sombreadores. Para este propósito, transferiremos los vectores de tangente y bi-tangente previamente preparados al sombreador de vértices a través de los atributos de vértice:

 #version 330 core layout (location = 0) in vec3 aPos; layout (location = 1) in vec3 aNormal; layout (location = 2) in vec2 aTexCoords; layout (location = 3) in vec3 aTangent; layout (location = 4) in vec3 aBitangent; 

En el código del vértice del sombreador mismo, formamos la matriz directamente:

 void main() { [...] vec3 T = normalize(vec3(model * vec4(aTangent, 0.0))); vec3 B = normalize(vec3(model * vec4(aBitangent, 0.0))); vec3 N = normalize(vec3(model * vec4(aNormal, 0.0))); mat3 TBN = mat3(T, B, N) } 

En el código anterior, primero convertimos todos los vectores de la base del espacio tangente en un sistema de coordenadas en el que nos sentimos cómodos trabajando; en este caso, este es el sistema de coordenadas mundial y multiplicamos los vectores por el modelo de matriz modelo . A continuación, creamos la matriz TBN en sí misma simplemente pasando los tres vectores correspondientes a un constructor de tipo mat3 . Tenga en cuenta que para la exactitud del orden de cálculo, es necesario multiplicar los vectores no por la matriz modelo, sino por la matriz normal, ya que solo estamos interesados ​​en la orientación de los vectores, pero no en su desplazamiento o escala

Estrictamente hablando, no es necesario transferir el vector bi-tangente al sombreador.
Como el triple de los vectores TBN es mutuamente perpendicular, la bi-tangente se puede encontrar en el sombreador mediante la multiplicación vectorial:

  vec3 B = cross(N, T) 

Entonces, se recibe la matriz TBN, ¿cómo la usamos? De hecho, hay dos enfoques para su uso en el mapeo normal:

1. Use la matriz TBN para transformar todos los vectores necesarios de la tangente al espacio mundial. Transfiera los resultados al sombreador de fragmentos, donde, también utilizando la matriz, transforme el vector del mapa normal al espacio mundial. Como resultado, el vector normal estará en el espacio donde se calcula toda la iluminación.
2. Tome la matriz inversa a TBN y convierta todos los vectores necesarios del espacio mundial a tangente. Es decir use esta matriz para transformar los vectores involucrados en los cálculos de iluminación en espacio tangente. El vector normal en este caso también permanece en el mismo espacio que los otros participantes en el cálculo de la iluminación.

Veamos la primera opción. El vector normal de la textura correspondiente se especifica en el espacio tangente, mientras que los otros vectores utilizados en el cálculo de la iluminación se definen en el espacio mundial. Al pasar la matriz TBN al sombreador de fragmentos, podríamos transformar el vector normal obtenido mediante el muestreo de la textura del espacio tangente al mundo, asegurando la unidad de los sistemas de coordenadas para todos los elementos del cálculo de la iluminación. En este caso, todos los cálculos (especialmente las multiplicaciones de vectores escalares) serán correctos.

La transferencia de la matriz TBN se realiza de la manera más simple:

 out VS_OUT { vec3 FragPos; vec2 TexCoords; mat3 TBN; } vs_out; void main() { [...] vs_out.TBN = mat3(T, B, N); } 

En el código del sombreador de fragmentos, respectivamente, establecemos una variable de entrada de tipo mat3:

 in VS_OUT { vec3 FragPos; vec2 TexCoords; mat3 TBN; } fs_in; 

Con la matriz a mano, puede especificar el código para obtener lo normal mediante la expresión de la traducción de la tangente al espacio mundial:

 normal = texture(normalMap, fs_in.TexCoords).rgb; normal = normalize(normal * 2.0 - 1.0); normal = normalize(fs_in.TBN * normal); 

Como la normal resultante ahora se establece en el espacio mundial, no hay necesidad de cambiar nada más en el código del sombreador. Cálculos de iluminación, y así asume un vector normal dado en coordenadas mundiales.

Veamos también el segundo enfoque.Se requerirá obtener la matriz TBN inversa, así como transferir todos los vectores involucrados en el cálculo de la iluminación del sistema de coordenadas mundial al que corresponde a los vectores normales obtenidos de la textura: la tangente. En este caso, la formación de la matriz TBN permanece sin cambios, pero antes de pasar al sombreador de fragmentos debemos obtener la matriz inversa:

 vs_out.TBN = transpose(mat3(T, B, N)); 

Tenga en cuenta que la función transpose () se usa en lugar de inverse () . Dicha sustitución es verdadera, ya que para las matrices ortogonales (donde todos los ejes están representados por unidades de vectores perpendiculares entre sí), la obtención de la matriz inversa da un resultado idéntico a la transposición. Y esto es muy útil, ya que, en el caso general, calcular la matriz inversa es una tarea mucho más costosa computacionalmente en comparación con la transposición.

En el código de sombreador de fragmentos, no convertiremos el vector normal, en su lugar, convertiremos otros vectores importantes del sistema de coordenadas del mundo a la tangente, es decir, lightDir y viewDir. Esta solución también reúne todos los elementos de los cálculos en un solo sistema de coordenadas, esta vez la tangente.

 void main() { vec3 normal = texture(normalMap, fs_in.TexCoords).rgb; normal = normalize(normal * 2.0 - 1.0); vec3 lightDir = fs_in.TBN * normalize(lightPos - fs_in.FragPos); vec3 viewDir = fs_in.TBN * normalize(viewPos - fs_in.FragPos); [...] } 

El segundo enfoque parece más lento y requiere más multiplicaciones de matriz en el sombreador de fragmentos (lo que afecta en gran medida el rendimiento). ¿Por qué empezamos a desmontarlo?
El hecho es que traducir vectores de coordenadas mundiales a tangentes proporciona una ventaja adicional: de hecho, ¡podemos mover todo el código de transformación del fragmento al sombreador de vértices! Este enfoque funciona porque lightPos y viewPos no cambian de fragmento a fragmento, y el valor es fs_in.FragPosTambién podemos traducir al espacio tangente en el sombreador de vértices, el valor interpolado en la entrada del sombreador de fragmentos será bastante correcto. Por lo tanto, para el segundo enfoque, no es necesario traducir todos estos vectores en el espacio tangente en el código del sombreador de fragmentos, mientras que el primero lo requiere, porque lo normal es único para cada fragmento.

Como resultado, nos alejamos de transferir la matriz inversa a TBN al sombreador de fragmentos y, en su lugar, le pasamos el vector de posición del vértice, la fuente de luz y el observador en el espacio tangente. Por lo tanto, eliminaremos las costosas multiplicaciones de matrices en el sombreador de fragmentos, lo que será una optimización significativa, porque el sombreador de vértices se ejecuta con mucha menos frecuencia. Es esta ventaja la que coloca el segundo enfoque en la categoría de uso preferido en la mayoría de los casos.

 out VS_OUT { vec3 FragPos; vec2 TexCoords; vec3 TangentLightPos; vec3 TangentViewPos; vec3 TangentFragPos; } vs_out; uniform vec3 lightPos; uniform vec3 viewPos; [...] void main() { [...] mat3 TBN = transpose(mat3(T, B, N)); vs_out.TangentLightPos = TBN * lightPos; vs_out.TangentViewPos = TBN * viewPos; vs_out.TangentFragPos = TBN * vec3(model * vec4(aPos, 0.0)); 

En el sombreador de fragmentos, cambiamos al uso de nuevas variables de entrada en los cálculos de iluminación en el espacio tangente. Como las normales se definen condicionalmente en este espacio, todos los cálculos siguen siendo correctos.
Ahora que todos los cálculos de mapeo normales se realizan en el espacio tangente, podemos cambiar la orientación de la superficie de prueba en la aplicación como queramos y la iluminación seguirá siendo correcta:

 glm::mat4 model(1.0f); model = glm::rotate(model, (float)glfwGetTime() * -10.0f, glm::normalize(glm::vec3(1.0, 0.0, 1.0))); shader.setMat4("model", model); RenderQuad(); 

De hecho, exteriormente todo se ve como debería:


Las fuentes están aquí .

Objetos complejos

Entonces, descubrimos cómo realizar un mapeo normal en el espacio tangente y cómo calcular independientemente los vectores tangentes y tangentes de polarización para esto. Afortunadamente, este cálculo manual no suele ser una tarea: en su mayor parte, los desarrolladores implementan este código en algún lugar de las entrañas del cargador de modelos. En nuestro caso, esto es cierto para el cargador Assimp utilizado .

Assimp proporciona un indicador de opción muy útil al cargar modelos: aiProcess_CalcTangentSpace . Cuando se pasa a la función ReadFile () , la propia biblioteca calculará las líneas de tangente suave y bi-tangente para cada uno de los vértices cargados, un proceso similar al discutido aquí.

 const aiScene *scene = importer.ReadFile( path, aiProcess_Triangulate | aiProcess_FlipUVs | aiProcess_CalcTangentSpace ); 

Después de eso, puede acceder directamente a las tangentes calculadas:

 vector.x = mesh->mTangents[i].x; vector.y = mesh->mTangents[i].y; vector.z = mesh->mTangents[i].z; vertex.Tangent = vector; 

También deberá actualizar el código de descarga para tener en cuenta la recepción de mapas normales para modelos texturizados. El formato Wavefront Object (.obj) exporta mapas normales de tal manera que el indicador Assimp aiTextureType_NORMAL no garantiza que estos mapas se carguen correctamente, mientras que todo funciona correctamente con el indicador aiTextureType_HEIGHT . Por lo tanto, personalmente, suelo cargar mapas normales de la siguiente manera:

 vector<Texture> normalMaps = loadMaterialTextures(material, aiTextureType_HEIGHT, "texture_normal"); 

Por supuesto, este enfoque puede no ser adecuado para otros formatos de descripción de modelos y tipos de archivos. También noto que configurar el indicador aiProcess_CalcTangentSpace no siempre funciona. Sabemos que el cálculo de tangentes se basa en coordenadas de textura, sin embargo, a menudo los autores de modelos aplican varios trucos a las coordenadas de textura, lo que interrumpe el cálculo de tangentes. Por lo tanto, una imagen especular de coordenadas de textura a menudo se usa para modelos con textura simétrica. Si no se tiene en cuenta el reflejo, el cálculo de las tangentes será incorrecto. Assimp no hace esta contabilidad. El modelo de nanotraje familiar aquí no es adecuado para la demostración, ya que también utiliza la duplicación.

Pero con un modelo correctamente texturizado que utiliza mapas normales y especulares, la aplicación de prueba ofrece un resultado muy bueno:


Como puede ver, el uso del mapeo normal proporciona un aumento tangible en los detalles y es barato en términos de costos de rendimiento.

No olvide que el uso del mapeo normal puede ayudar a mejorar el rendimiento de una escena en particular. Sin su uso, lograr el detalle del modelo solo es posible al aumentar la densidad de la malla poligonal, malla. Pero esta técnica le permite alcanzar visualmente el mismo nivel de detalle para mallas de baja poli. A continuación puede ver una comparación de estos dos enfoques:


El nivel de detalle en el modelo de alta poli y en el modelo de baja poli que utiliza el mapeo normal es prácticamente indistinguible. Por lo tanto, esta técnica es una excelente manera de reemplazar modelos de alta poli en la escena con modelos simplificados, prácticamente sin pérdida de calidad visual.

Ultimo comentario

Hay otro detalle técnico sobre el mapeo normal, que mejora un poco la calidad con poco o ningún costo adicional.

En los casos en que las tangentes se calculan para mallas grandes y complejas con un número significativo de vértices que pertenecen a varios triángulos, los vectores tangentes generalmente se promedian para obtener un resultado de mapeo normal suave y visualmente agradable. Sin embargo, esto crea un problema: después del promedio, el triple de los vectores TBN puede perder perpendicularidad mutua, lo que también significa la pérdida de ortogonalidad para la matriz TBN. En el caso general, el resultado del mapeo normal obtenido sobre la base de una matriz no ortogonal es solo ligeramente incorrecto, pero aún podemos mejorarlo.

Para hacer esto, es suficiente aplicar un método matemático simple:Proceso de Gram-Schmidt o re-ortogonalización de nuestro triple de vectores TBN. En el código del sombreador de vértices:

 vec3 T = normalize(vec3(model * vec4(aTangent, 0.0))); vec3 N = normalize(vec3(model * vec4(aNormal, 0.0))); // - T  N T = normalize(T - dot(T, N) * N); //    B    T  N vec3 B = cross(N, T); mat3 TBN = mat3(T, B, N) 

Esta enmienda, aunque pequeña, mejora la calidad del mapeo normal a cambio de los gastos generales exiguos. Si está interesado en los detalles de este procedimiento, puede ver la última parte del video Normal Mapping Mathematics, cuyo enlace se proporciona a continuación.

Recursos Adicionales

• Tutorial 26: Mapeo normal : una lección sobre mapeo normal de ogldev .
• Cómo funciona la asignación normal : un video tutorial que explica los conceptos básicos de la asignación normal de TheBennyBox .
• Mapeo de Mapeo Normal : Una película relacionada con la anterior que explica las matemáticas utilizadas en el método de Mapeo Normal, también de TheBennyBox .
• Tutorial 13: Mapeo normal : otra lección de opengl-tutorial.org .

PD : Tenemos un telegrama conf para la coordinación de transferencias. Si tiene un serio deseo de ayudar con la traducción, ¡de nada!