La dinámica del vuelo vertical de un avión más ligero que el aire.

Introduccion

Determinar la velocidad de ascenso y descenso de aviones más ligeros que el aire (LALV) hasta la fecha es casi una tarea importante que surge en el diseño de tales dispositivos.

Una gran cantidad de publicaciones están dedicadas a LALF, por ejemplo, solo en nuestro recurso hay dos artículos muy interesantes [1,2] relacionados con la historia del desarrollo en el ejemplo de diseños específicos de aeronaves y estratostatos. Sin embargo, hay muy pocos cálculos de la dinámica del vuelo vertical de tales dispositivos, lo que permite determinar al menos aproximadamente la velocidad de ascenso y descenso de las APAL.

La última declaración requiere una cierta explicación, ya que un lector experimentado recuerda el curso de física de la escuela, en el que se resolvieron problemas sobre la altura de elevación y otros parámetros de globos llenos de gases más livianos que el aire o por el aire calentado durante el vuelo.

Todas estas tareas se basaron en la igualdad de dos fuerzas: la fuerza del peso y la fuerza de flotabilidad. Los gases se consideraron ideales y sus parámetros se calcularon de acuerdo con la ley de Mendeleev Clapeyron. Sin embargo, incluso un simple cálculo de la tercera fuerza de resistencia al aire ya conduce a un sistema de ecuaciones diferenciales, que no puede resolverse analíticamente. También es necesario tener en cuenta el cambio en la densidad del aire atmosférico con la altura de elevación y la temperatura.

Además, si necesita considerar no solo el ascenso, sino también el congelamiento de la pelota y su descenso al suelo, entonces no es en absoluto una tarea de niños. Espero que la consideración de la solución de un problema similar mediante Python no solo contribuya a la expansión del conocimiento en física, sino también a la popularización del lenguaje de programación Python. Lo que trato de hacer en mis publicaciones sobre este recurso.

Un modelo matemático del vuelo de un LALV con un caparazón en forma de bola, cuyo volumen no cambia con la altura.

Nos limitamos a considerar el movimiento de su centro de masa bajo la acción de las siguientes fuerzas: gravedad ( G ), fuerza de Arquímedes ( Fa ) y fuerza de arrastre aerodinámica ( Fc ). Escribimos las relaciones para determinar las fuerzas a través de los parámetros de movimiento y el ambiente aéreo [3]:





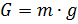
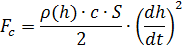
En las fórmulas anteriores, se utiliza la notación: h es la altura de la pelota, dh / dt es la velocidad vertical, m es la masa, g es la aceleración de la gravedad, W es el volumen de la pelota, c es el coeficiente de arrastre, S es el área característica de resistencia (área intermedia).
Se supondrá que la dependencia de la densidad del aire con la altura es exponencial:



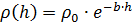
donde $$$ρ_0$- densidad del aire a altura cero, coeficiente b. La fuerza de la gravedad se dirige hacia abajo, la fuerza de Arquímedes se dirige hacia arriba y la fuerza de la resistencia aerodinámica siempre se dirige "contra el movimiento", por lo tanto, la inclusión correcta de esta fuerza en las ecuaciones de movimiento requiere la introducción de un factor $$$-sing (dh / dt)$.

Sin embargo, para nuestros propósitos, este hecho no es de importancia fundamental, y nos limitamos a considerar solo la etapa de elevar la pelota, cuando la fuerza de arrastre aerodinámico se dirige hacia abajo y, por lo tanto, se tendrá en cuenta en las ecuaciones de movimiento con un signo menos. Ahora la ecuación de movimiento se puede escribir como:

, (1)

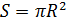
Además, suponga que el globo es un cuerpo homogéneo de radio R con densidad $$$ρ_b$. Luego, el tamaño del área que determina su resistencia aerodinámica se define como volumen como y masa, respectivamente, como .

Ahora está claro que cada término de la ecuación (1) contiene S. como factor. Por lo tanto, cada término de la ecuación de movimiento puede reducirse por un factor de S. La ecuación misma tomará la forma:

, (2)

Presentamos la siguiente notación:

;
;

y reescribir (2) en la forma del siguiente sistema de ecuaciones no lineales:

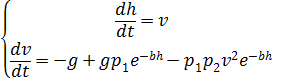
, (3)

Influencia en la velocidad y altura del aumento de la temperatura del aire LALV

Para hacer esto, primero resolvemos el sistema (3) usando la siguiente relación para la dependencia de la densidad del aire atmosférico de la altura sin tener en cuenta la temperatura:



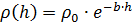
Repitamos la solución del sistema (3), pero usando la relación para la dependencia de la densidad del aire de la altitud y la temperatura:



donde: b = 0.000125 es una constante asociada con una densidad del aire de 1 / m;
a = 0.0065 es una constante relacionada con la temperatura del aire en K / m.
$$$T_0 = 300 K$- temperatura al nivel del mar.


Obtenemos:



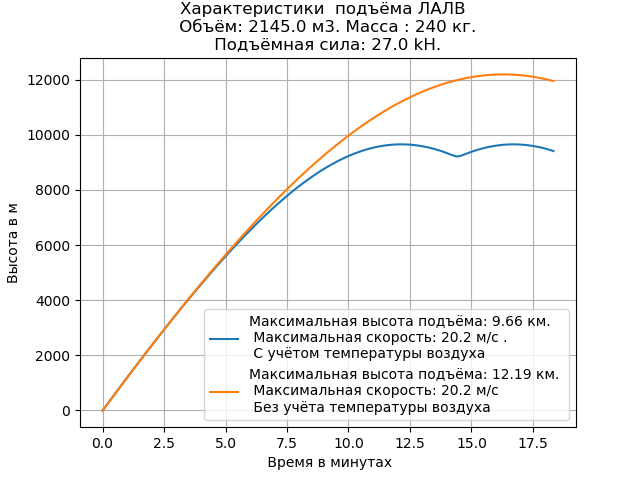
El valor calculado de la altura del elevador LALV, teniendo en cuenta la temperatura, es menor que sin tener en cuenta. La velocidad de elevación del aparato permanece sin cambios.

Determinación de las características de todas las fases del vuelo SALV desde el inicio hasta el aterrizaje.

Para construir el programa de vuelo LALV considere las condiciones para los siguientes períodos de tiempo:

Rise - ;
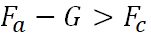
Colgar - ;
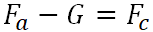
Aterrizaje - .


Obtenemos:



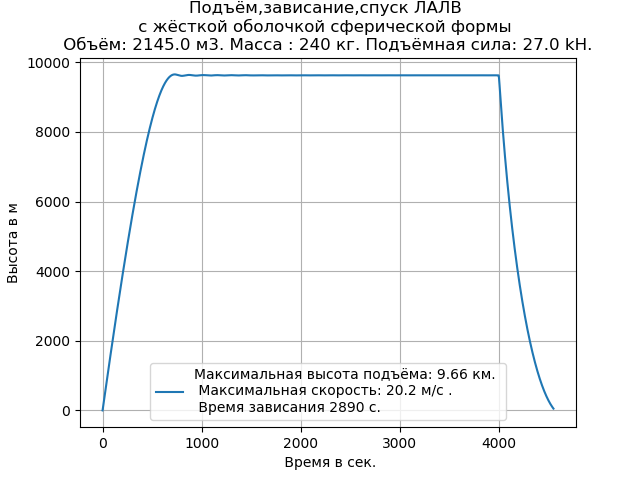
Como se desprende del gráfico y la lista del programa, para realizar un experimento computacional, es suficiente ingresar los datos iniciales necesarios.

Un modelo matemático del vuelo de un LALV con una carcasa, cuyo volumen varía con la altura.

Tales LALV incluyen estratostatos. El globo estratosférico no se puede inflar completamente con helio, dándole la máxima fuerza de elevación, que convertirá la forma de su caparazón en una bola. Tal bola a gran altitud puede explotar debido a la mayor diferencia en las presiones internas y externas.

Por estas razones, para calcular la altura de elevación máxima alcanzable, se introducen dos valores de su volumen: el Vmin mínimo y el Vmax máximo, respectivamente. Teniendo en cuenta las variables introducidas y la dependencia de la densidad del aire en la altura, las relaciones para la fuerza de flotabilidad Fa y la fuerza de gravedad Ft toman la forma:

, (4)

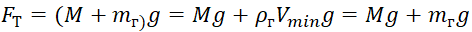
, (5)

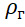
donde: M es la masa de la carcasa y el equipo del globo estratosférico; Es la densidad del helio.

Al igualar las relaciones (4) y (5), suponiendo que el volumen del caparazón V es una función de la altura del LALV, obtenemos la relación:

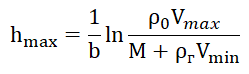
. (6)

Los valores numéricos de los parámetros incluidos en la relación (6) se dan en el listado para construir un gráfico, que se da solo para el propósito indicado.


Obtenemos:



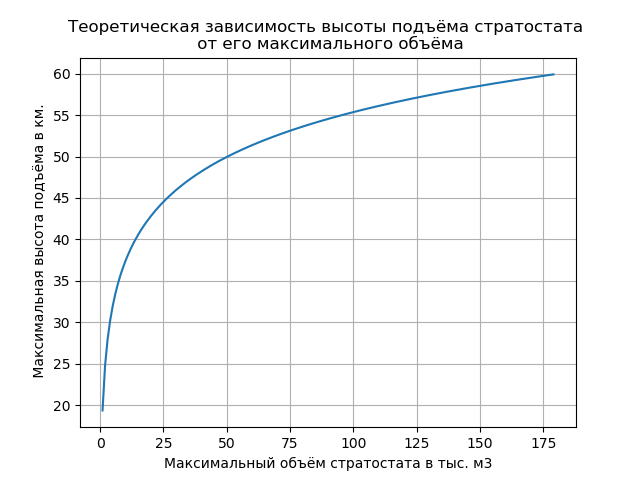
Al cambiar los parámetros de LALV que figuran en la lista del programa, puede obtener el gráfico dado y seleccionar el volumen de shell máximo requerido durante el diseño. El refinamiento de los resultados se lleva a cabo utilizando una vasta experiencia en la creación de tales dispositivos.

Conclusiones:

1. Se obtienen modelos matemáticos de dos tipos de aeronaves más livianas que el aire, que permiten que los experimentos computacionales evalúen los parámetros de dichos dispositivos en condiciones idealizadas del ambiente aéreo.
   
2. El esquema de etapas múltiples propuesto para la solución numérica del sistema de ecuaciones diferenciales permite obtener la trayectoria vertical de un avión más ligero que el aire en las etapas de ascenso y descenso.
   

Referencias

1. Algunas palabras sobre aeronaves
   
2. En el camino al espacio. Estratostatos
   
3. Ryzhikov Yu.I. Fortran moderno. - San Petersburgo: impresión de la corona, 2004 .-- 288 p.