AI, curso práctico. Descripción general de las redes neuronales para la clasificación de imágenes

Este artículo proporciona una visión general teórica accesible de las redes neuronales convolucionales (CNN) y explica su aplicación al problema de clasificación de imágenes.

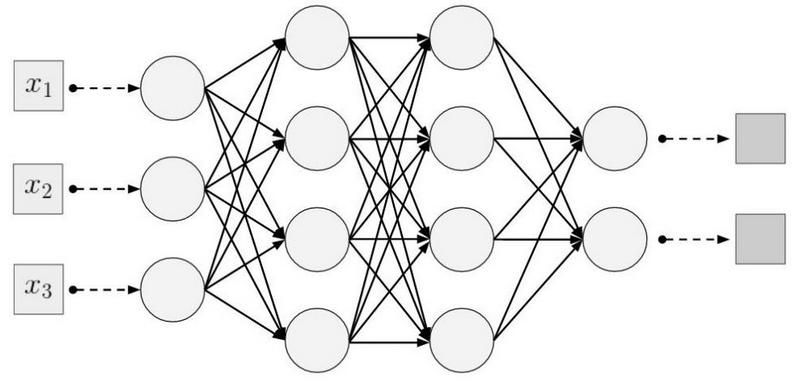
Enfoque común: sin aprendizaje profundo

El término "procesamiento de imágenes" se refiere a una amplia clase de tareas para las cuales los datos de entrada son imágenes, y la salida puede ser imágenes o conjuntos de características asociadas. Hay muchas opciones: clasificación, segmentación, anotación, detección de objetos, etc. En este artículo, examinamos la clasificación de imágenes, no solo porque es la tarea más simple, sino también porque subyace a muchas otras tareas.

El enfoque general para la clasificación de imágenes consta de los siguientes dos pasos:

1. Generación de características significativas de la imagen.
2. Clasificación de una imagen en función de sus atributos.

La secuencia común de operaciones utiliza modelos simples como MultiLayer Perceptron (MLP), Support Vector Machine (SVM), k método de vecinos más cercanos y regresión logística sobre las características creadas manualmente. Los atributos se generan usando varias transformaciones (por ejemplo, detección de umbral y escala de grises) y descriptores, por ejemplo, histograma de gradientes orientados ( HOG ) o transformaciones de transformación de características invariantes de escala ( SIFT ), y etc.

La principal limitación de los métodos generalmente aceptados es la participación de un experto que elige un conjunto y una secuencia de pasos para generar características.

Con el tiempo, se notó que la mayoría de las técnicas para generar características se pueden generalizar utilizando núcleos (filtros): matrices pequeñas (generalmente de tamaño 5 × 5), que son convoluciones de las imágenes originales. La convolución puede considerarse como un proceso secuencial de dos etapas:

1. Pase el mismo núcleo fijo en toda la imagen de origen.
2. En cada paso, calcule el producto escalar del núcleo y la imagen original en la ubicación actual del núcleo.

El resultado de la convolución de la imagen y el núcleo se denomina mapa de características.
Una explicación matemáticamente más rigurosa se da en el capítulo correspondiente del libro recientemente publicado, Aprendizaje profundo, de I. Goodfellow, I. Benjio y A. Courville.


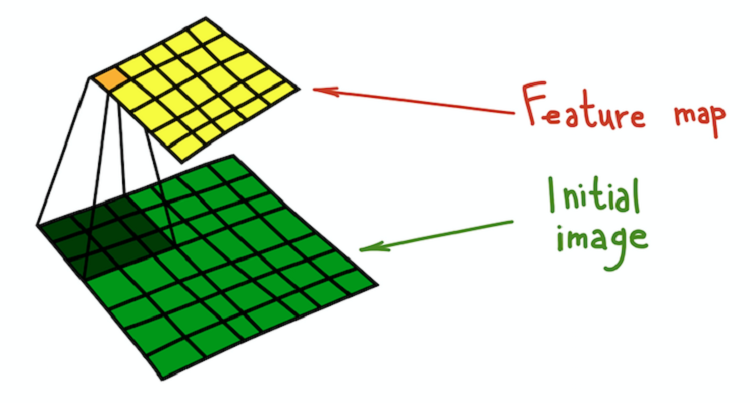El proceso de convolución del núcleo (verde oscuro) con la imagen original (verde), como resultado de lo cual se obtiene un mapa de características (amarillo).

Un ejemplo simple de una transformación que se puede hacer con filtros es desenfocar una imagen. Tome un filtro que consta de todas las unidades. Calcula el promedio del vecindario determinado por el filtro. En este caso, el vecindario es una sección cuadrada, pero puede ser cruciforme o cualquier otra cosa. El promedio lleva a la pérdida de información sobre la posición exacta de los objetos, lo que hace borrosa toda la imagen. Se puede dar una explicación intuitiva similar para cualquier filtro creado manualmente.


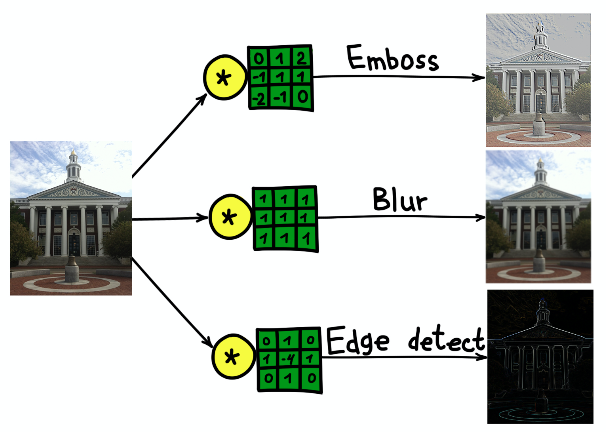El resultado de la convolución de la imagen del edificio de la Universidad de Harvard con tres núcleos diferentes.

Redes neuronales convolucionales

El enfoque convolucional para la clasificación de imágenes tiene una serie de inconvenientes importantes:

• Un proceso de varios pasos en lugar de una secuencia de extremo a extremo.
• Los filtros son una gran herramienta de generalización, pero son matrices fijas. ¿Cómo elegir pesos en filtros?

Afortunadamente, se han inventado filtros que se pueden aprender, que son el principio básico de CNN. El principio es simple: entrenaremos los filtros aplicados a la descripción de las imágenes para cumplir mejor su tarea.

CNN no tiene un inventor, pero uno de los primeros casos de su aplicación es LeNet-5 * en el trabajo " Aprendizaje basado en el gradiente aplicado al reconocimiento de documentos" por I. LeCun y otros autores.

CNN mata a dos pájaros de un tiro: no hay necesidad de una definición preliminar de los filtros, y el proceso de aprendizaje se vuelve de extremo a extremo. Una arquitectura típica de CNN consta de las siguientes partes:

• Capas convolucionales
• Capas de submuestreo
• Capas densas (completamente conectadas)

Consideremos cada parte con más detalle.

Capas convolucionales

La capa convolucional es el principal elemento estructural de CNN. La capa convolucional tiene un conjunto de características:
Conectividad local (escasa) . En las capas densas, cada neurona está conectada a cada neurona de la capa anterior (por lo tanto, se llamaron densas). En la capa convolucional, cada neurona está conectada solo a una pequeña parte de las neuronas de la capa anterior.


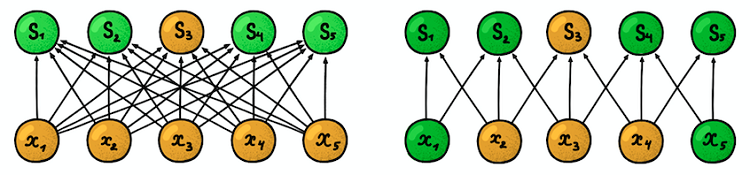Un ejemplo de una red neuronal unidimensional. (izquierda) Conexión de neuronas en una red densa típica, (derecha) Caracterización de la conectividad local inherente a la capa convolucional. Imágenes tomadas de I. Goodfellow y otros por Deep Learning

El tamaño del área a la que está conectada la neurona se denomina tamaño del filtro (la longitud del filtro en el caso de datos unidimensionales, por ejemplo, series de tiempo, o el ancho / alto en el caso de datos bidimensionales, por ejemplo, imágenes). En la figura de la derecha, el tamaño del filtro es 3. Los pesos con los que se realiza la conexión se denominan filtro (un vector en el caso de datos unidimensionales y una matriz para datos bidimensionales). El paso es la distancia que el filtro se mueve sobre los datos (en la figura de la derecha, el paso es 1). La idea de conectividad local no es más que un núcleo que se mueve un paso. Cada neurona de nivel convolucional representa e implementa una posición específica del núcleo deslizándose a lo largo de la imagen original.


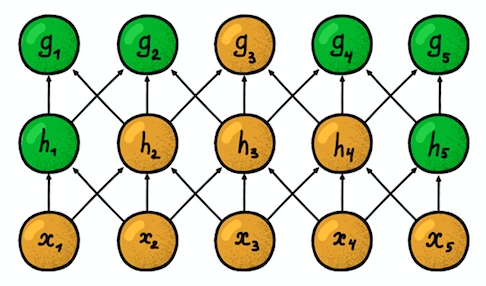Dos capas convolucionales unidimensionales adyacentes

Otra propiedad importante es la llamada zona de susceptibilidad . Refleja el número de posiciones de la señal original que la neurona actual puede "ver". Por ejemplo, la zona de susceptibilidad de la primera capa de red, que se muestra en la figura, es igual al tamaño del filtro 3, ya que cada neurona está conectada a solo tres neuronas de la señal original. Sin embargo, en la segunda capa, la zona de susceptibilidad ya es 5, ya que la neurona de la segunda capa agrega tres neuronas de la primera capa, cada una de las cuales tiene una zona de susceptibilidad 3. Con una profundidad creciente, la zona de susceptibilidad crece linealmente.

Parámetros compartidos Recuerde que en el procesamiento clásico de imágenes, el mismo núcleo se deslizó por toda la imagen. La misma idea se aplica aquí. Solo fijamos el tamaño del filtro de pesos para una capa y aplicaremos estos pesos a todas las neuronas de la capa. Esto es equivalente a deslizar el mismo núcleo por toda la imagen. Pero puede surgir la pregunta: ¿cómo podemos aprender algo con un número tan pequeño de parámetros?


Las flechas oscuras representan los mismos pesos. (izquierda) MLP regular, donde cada factor de ponderación es un parámetro separado, (derecha) Un ejemplo de separación de parámetros, donde varios factores de ponderación indican el mismo parámetro de entrenamiento

Estructura espacial . La respuesta a esta pregunta es simple: ¡entrenaremos varios filtros en una capa! Se colocan paralelos entre sí, formando así una nueva dimensión.

Hacemos una pausa breve y explicamos la idea presentada por el ejemplo de una imagen RGB bidimensional de 227 × 227. Tenga en cuenta que aquí se trata de una imagen de entrada de tres canales, lo que, en esencia, significa que tenemos tres imágenes de entrada o datos de entrada tridimensionales.


La estructura espacial de la imagen de entrada.

Consideraremos las dimensiones de los canales como la profundidad de la imagen (tenga en cuenta que esto no es lo mismo que la profundidad de las redes neuronales, que es igual al número de capas de red). La pregunta es cómo determinar el núcleo para este caso.


Un ejemplo de un núcleo bidimensional, que es esencialmente una matriz tridimensional con una medición de profundidad adicional. Este filtro da una convolución con la imagen; es decir, se desliza sobre la imagen en el espacio, calculando productos escalares

La respuesta es simple, aunque todavía no es obvia: haremos que el núcleo también sea tridimensional. Las dos primeras dimensiones seguirán siendo las mismas (ancho y alto del núcleo), y la tercera dimensión siempre es igual a la profundidad de los datos de entrada.


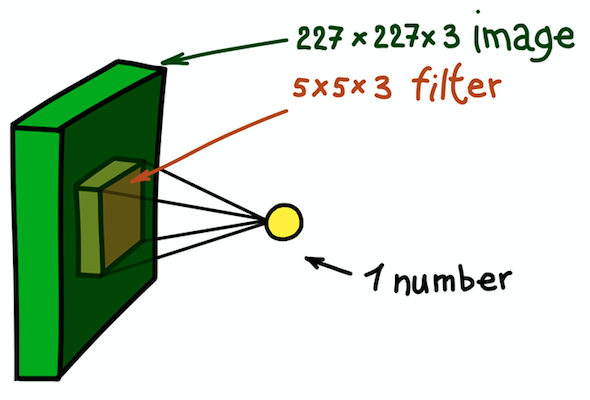Un ejemplo de un paso de convolución espacial. El resultado del producto escalar del filtro y una pequeña porción de la imagen 5 × 5 × 3 (es decir, 5 × 5 × 5 + 1 = 76, la dimensión del producto escalar + desplazamiento) es un número

En este caso, toda la sección 5 × 5 × 3 de la imagen original se transforma en un número, y la imagen tridimensional en sí se transformará en un mapa de características ( mapa de activación ). Un mapa de características es un conjunto de neuronas, cada una de las cuales calcula su propia función, teniendo en cuenta dos principios básicos discutidos anteriormente: conectividad local (cada neurona está asociada con solo una pequeña parte de los datos de entrada) y separación de parámetros (todas las neuronas usan el mismo filtro). Idealmente, este mapa de características será el mismo que el que se encuentra en el ejemplo de una red generalmente aceptada: almacena los resultados de convolución de la imagen de entrada y el filtro.


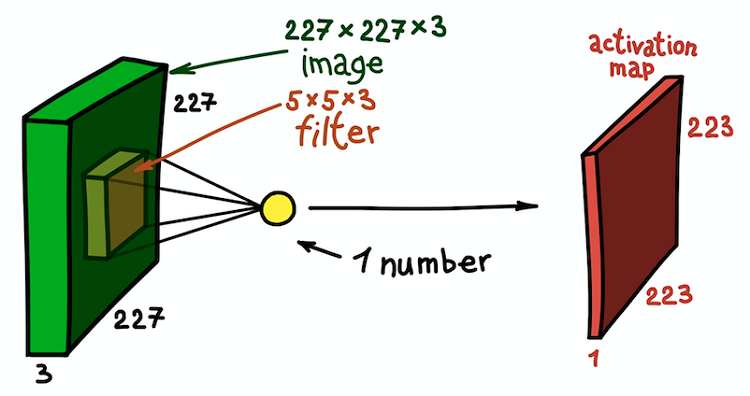Mapa de características como resultado de la convolución del núcleo con todas las posiciones espaciales

Tenga en cuenta que la profundidad del mapa de entidades es 1, ya que solo usamos un filtro. Pero nada nos impide usar más filtros; por ejemplo, 6. Todos ellos interactuarán con los mismos datos de entrada y funcionarán independientemente uno del otro. Vayamos un paso más allá y combinemos estas tarjetas de características. Sus dimensiones espaciales son las mismas ya que las dimensiones de los filtros son las mismas. Por lo tanto, los mapas de características recopilados juntos pueden considerarse como una nueva matriz tridimensional, cuya dimensión de profundidad está representada por mapas de características de diferentes núcleos. En este sentido, los canales RGB de la imagen de entrada no son otros que los tres mapas de características originales.


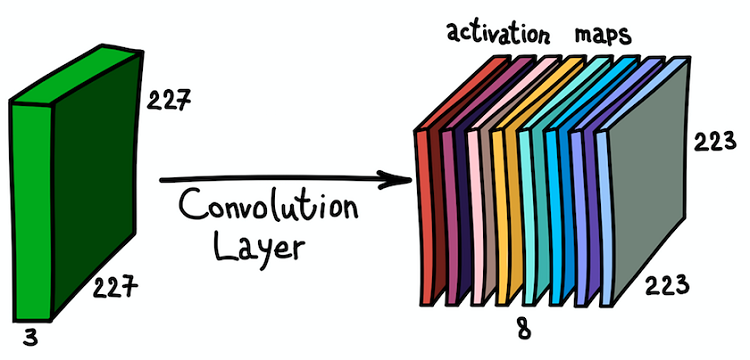La aplicación paralela de varios filtros a la imagen de entrada y el conjunto resultante de tarjetas de activación

Tal comprensión de los mapas de características y su combinación es muy importante, ya que, al darnos cuenta de esto, podemos expandir la arquitectura de red e instalar capas convolucionales una encima de la otra, aumentando así la zona de susceptibilidad y enriqueciendo nuestro clasificador.


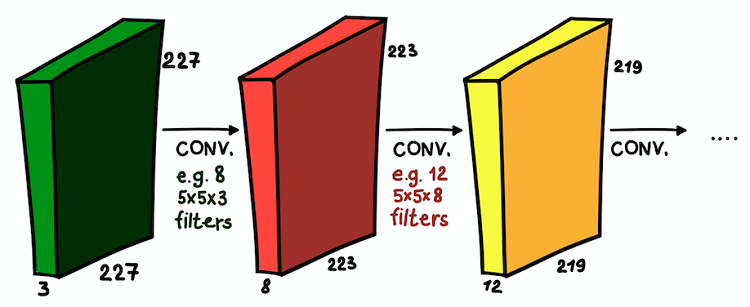Capas convolucionales instaladas una encima de la otra. En cada capa, el tamaño de los filtros y su número pueden variar.

Ahora entendemos qué es una red convolucional. El objetivo principal de estas capas es el mismo que con el enfoque generalmente aceptado: detectar signos significativos de la imagen. Y, si en la primera capa estos signos pueden ser muy simples (la presencia de líneas verticales / horizontales), la profundidad de la red aumenta el grado de su abstracción (la presencia de un perro / gato / persona).

Capas de submuestreo

Las capas convolucionales son el bloque de construcción principal de CNN. Pero hay otra parte importante y de uso frecuente: estas son capas de submuestra. En el procesamiento de imágenes convencional, no existe un análogo directo, pero una submuestra puede considerarse como otro tipo de núcleo. Que es esto


Ejemplos de submuestreo. (izquierda) Cómo una submuestra cambia los tamaños espaciales (¡pero no de canal!) de las matrices de datos, (derecha) Un esquema básico de cómo funciona una submuestra

Una submuestra filtra una parte de la vecindad de cada píxel de los datos de entrada con una función de agregación específica, por ejemplo, máximo, promedio, etc. La submuestra es esencialmente lo mismo que convolución, pero la función de combinación de píxeles no se limita al producto escalar. Otra diferencia importante es que el submuestreo solo funciona en la dimensión espacial. Un rasgo característico de la capa de submuestreo es que el tono suele ser igual al tamaño del filtro (el valor típico es 2).

Una submuestra tiene tres objetivos principales:

• Disminución de la dimensión espacial o submuestreo. Esto se hace para reducir el número de parámetros.
• El crecimiento de la zona de susceptibilidad. Debido a las neuronas de la submuestra en las capas posteriores, se acumulan más pasos de la señal de entrada
• Invarianza traslacional a pequeñas heterogeneidades en la posición de los patrones en la señal de entrada. Al calcular estadísticas de agregación de vecindades pequeñas de la señal de entrada, una submuestra puede ignorar pequeños desplazamientos espaciales en ella.

Capas gruesas

Las capas convolucionales y las capas de submuestra sirven al mismo propósito: generar atributos de imagen. El último paso es clasificar la imagen de entrada en función de las características detectadas. En CNN, las capas densas en la parte superior de la red hacen esto. Esta parte de la red se llama clasificación . Puede contener varias capas una encima de la otra con conectividad completa, pero generalmente termina con una capa de clase softmax activada por una función de activación logística multivariable , en la que el número de bloques es igual al número de clases. En la salida de esta capa está la distribución de probabilidad por clase para el objeto de entrada. Ahora la imagen se puede clasificar eligiendo la clase más probable.