"¡Pero hacemos cohetes!"

En un artículo anterior, verifiqué si es posible ajustar automáticamente un controlador difuso usando "métodos estándar" de optimización. Resultó ser posible y el resultado de la sintonización automática es bastante satisfactorio. Al menos para el cohete cuyo modelo se utilizó.

Para los objetos de control no estacionarios donde los parámetros del objeto varían en rangos amplios, un controlador difuso puede no proporcionar suficiente calidad de control en todos los rangos operativos. En este caso, es necesario utilizar un controlador difuso con "sintonización multicanal".

Verifiquemos si es posible configurar dicho regulador utilizando métodos de optimización estándar.
Considere la síntesis de un controlador difuso con sintonización multicanal para estabilizar un misil balístico en ángulo de cabeceo. Como se indica en los comentarios, el misil será FAU-2. Usamos un ejemplo del mismo libro de V. Gostev. "Reguladores difusos en sistemas de control automático".

Todos los términos utilizados en este texto están tomados de este libro y pueden no corresponder a la estricta terminología de la teoría del control automático.

Declaración del problema.

Un misil balístico que utiliza una gran cantidad de sistemas de control local es un objeto de control sustancialmente no estacionario. Las funciones de transferencia, que describen el cohete como un objeto de control, difieren de las funciones de transferencia de las aeronaves aladas en que tienen enlaces inestables, por lo que el movimiento de un cohete no controlado a lo largo de una ruta programada sería inestable.

A continuación consideramos el sistema de estabilización de un misil balístico en ángulo de cabeceo (canal de movimiento longitudinal). El sistema consta de los siguientes elementos funcionalmente necesarios:
un elemento de comparación (un giroscopio libre con un sensor potenciométrico caracterizado por coeficientes Kp);
amplificador de potencia Ku y engranaje de dirección hidráulica.

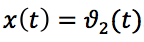
Tomando el ángulo de cabeceo como la coordenada de salida del cohete , para la coordenada de entrada - ángulo de dirección , definimos la función de transferencia en la forma:


(El engranaje de dirección analógico y el cohete están incluidos en el objeto de control) Los parámetros de la función de transferencia serán polinomios dependientes del tiempo. Matemáticamente, pueden determinarse por polinomios:











La tarea supone que el tiempo de inicio del vuelo es de 6 segundos. Los valores polinómicos se aceptan con un cambio de 6 segundos.
El modelo matemático del enlace oscilatorio no estacionario se describe mediante la ecuación diferencial:



El modelo matemático de un enlace forzado inestable se describe mediante la ecuación diferencial:



El error de desajuste en la entrada del controlador difuso es la diferencia entre el conjunto y el ángulo de paso requerido.

El diagrama estructural del modelo se muestra en la Figura 1. Para comprender el principio de formación del modelo, las líneas de comunicación indican las variables X1, X y sus derivadas ( X1 '', X1 '', X ' ) de acuerdo con las ecuaciones de los enlaces. El rectángulo verde indica la parte del circuito modelo que corresponde al enlace oscilante, y el amarillo es el enlace forzado.

Los parámetros a (t), b (t), c (t), r (t) se establecen en forma de factores de amplificación, en bloques del tipo "amplificador". Parámetro se establece en la ganancia del enlace integrador.


Figura 1. Diagrama estructural del modelo.

Ruta del software, dado el ángulo de paso u (t) = 1 + 0.5sin (πt / 30).
Los gráficos de los cambios en los parámetros del cohete durante el vuelo se presentan en la Figura 2.
El valor de t = 6 se toma como el inicio del vuelo; en la función polinómica, el valor (tiempo + 6) se usa para calcular los parámetros, donde el tiempo es el tiempo de simulación actual.


Figura 2. Gráficos de cambios en los parámetros del cohete.

Controlador lógico difuso

Como controlador basado en lógica difusa, utilizamos el controlador que se muestra en la Figura 3. Se aplica un desajuste entre el ángulo de paso dado y el ángulo de paso de misil real a la entrada.

El retardo de bloque por paso de cuantificación proporciona una discretización de la conversión de una señal continua en una discreta con un paso de muestreo de 0,01 segundos.

Usando dos retrasos más, la primera y la segunda desviación derivada se calculan mediante los métodos de diferencia en el paso de discretización.

Las unidades de fase calculan los valores de los términos para desviación, tasa de cambio y aceleración. (Para más información sobre esto, vea el texto anterior ). A la salida de cada bloque de fases, obtenemos un vector de términos para variables lingüísticas. (ver tabla 1)

Variable lingüística	Términos
Desviación	Más Norma Menos
Tasa de cambio	Esta creciendo No cambia Esta cayendo
Cambio más rápido	Está aumentando Constante Disminuye

Los bloques demultiplexores analizan los vectores en términos separados, que se transmiten a los bloques de procesamiento lógico de acuerdo con las reglas de inferencia difusa.
El resultado de la inferencia difusa también tiene tres variables lingüísticas: "reducir", "no cambiar", "aumentar". Las siguientes reglas de inferencia están escritas en forma de diagrama.

• Si Más y Creciente y la tasa de crecimiento aumentan >> disminuyen .
• Si la norma , y no cambia y es constante => no cambiamos .
• Si Less and Falls y la tasa de caída aumenta => aumenta .

Figura 3. Esquema de un regulador basado en lógica difusa.

En la desnazificación, las funciones triangulares con una base común se utilizan como una función de pertenencia (ver Fig. 4)

Figura 4. Funciones de fase triangular con una base común.

Se supone que las funciones son simétricas con respecto a 0, en este caso, para describir tres funciones triangulares, un valor de Max es suficiente. Para los que se muestran en la figura, Max = 30.

Las mismas funciones de membresía se utilizan para la salida.

Para una definición completa del regulador, es necesario establecer los valores máximos para los bloques de variableización de fase:

- deltaMax - desviación máxima;
- divMax: la derivada máxima de la desviación;
- div2Max - segunda derivada máxima de la desviación;
- uMax - acción de control máximo.

Optimización completa del proceso.

La acción de control máxima se toma igual a uMax - 70.
Por lo tanto, nos queda elegir 3 parámetros para la función de cambio de fase.
En este problema, el desajuste se alimenta mediante un paso en el momento cero del tiempo del modelo, u (t) = 1 + 0.5.sin (πt / 30).

La trayectoria programada, el ángulo de paso dado u (t) = 1 + 0.5sin (πt / 30), causa un efecto gradual en el primer segundo del proceso de transición, ya que resultó durante los experimentos con la tarea anterior, los controladores sintonizados a un proceso de control suave, con acción gradual, pueden no proporcionar la calidad requerida del proceso de transición.

Por lo tanto, para la optimización, formamos 3 criterios:

1. Tiempo transitorio: debemos llegar a una ruta de programa determinada lo más rápido posible.
2. Desviación estándar
3. Número de conmutaciones: en los experimentos con la tarea anterior, obtuvimos la opción cuando hubo oscilaciones de alta frecuencia de la acción de control en la salida del sistema de control.

El esquema general del bloque de optimización se muestra en la Figura 5.

Figura 5. Esquema del bloque de optimización.

Parámetros de entrada del bloque de optimización:

- desviación del ángulo de inclinación dado.
- impacto regulatorio.

Para calcular el tiempo transitorio, se usa un interruptor en el que el tiempo actual del modelo se aplica a una de las entradas. Después del bloque hay un retraso para el período de cuantificación, el valor del retraso se transmite a la segunda entrada.

Como interruptor, se utiliza un módulo de desviación. Si el módulo de desviación es mayor que el valor de conmutación establecido (0.02), el tiempo actual se emite en el bloque; si el módulo es menor que el valor establecido, el tiempo almacenado cuando la desviación fue mayor se transmite a la salida. Si la desviación nuevamente excede el límite, nuevamente obtenemos el tiempo. Por lo tanto, a la salida siempre tenemos la última vez que la desviación excedió el valor establecido.
Como unidad de conmutación, el signo de la acción de control cambia de + a -. Para calcular el número de conmutaciones, utilizamos el bloque "impulso a lo largo del frente" que, cuando la entrada se cambia de 0 a 1, da un pulso de duración en el paso de integración, el integrador calcula los impulsos. A la salida del bloque: la cantidad de cambios.

- El bloque de optimización selecciona los valores de los parámetros que se optimizarán de forma que se minimicen los tres parámetros:
- deltaMax - desviación máxima;
- divMax: la derivada máxima de la desviación;
- div2Max: la segunda derivada máxima de la desviación.

El resultado es la optimización del proceso de transición completo.

Después de comenzar el proceso de optimización, obtuvimos los siguientes parámetros óptimos para el controlador difuso:

- deltaMax = 0.185– desviación máxima;
- divMax = 0.278 - la derivada máxima de la desviación;
- div2Max = 1.291 - la segunda derivada máxima de la desviación.

Los resultados del proceso optimizado se muestran en la Figura 6.

Figura 6a. El proceso de transición.

Figura 6b. Opciones de control.

Se puede ver que la optimización, en general, fue un éxito, pero existen desviaciones del ángulo de paso dado casi a lo largo del proceso. El gráfico de desviación ampliado muestra que las desviaciones después de la optimización y la finalización del proceso de transición están en el rango de 0.015 - 0.02. (ver figura 7)

Figura 7. Desviación en el proceso de control.

Optimización por tramos de vuelo.

Intentemos mejorar el proceso seleccionando los parámetros del controlador difuso para diferentes secciones del vuelo del cohete.

La primera sección es el tiempo desde el inicio hasta la salida en una ruta determinada. Basado en el gráfico de desviación, el proceso de transición asociado con el efecto paso a paso inicial termina en algún lugar a los 20 segundos. (ver figura 7). En esta sección, se produce la optimización del tiempo del proceso de transición.

Establezca el tiempo de finalización del cálculo en 20 segundos. Y realizaremos la optimización, eliminando la desviación estándar de los criterios. Optimizaremos el tiempo del proceso de transición y el número de cambios. El diagrama de bloques de optimización se muestra en la Figura 8.


Figura 8. Esquema de optimización en la primera fase de vuelo.

La optimización automática para la primera fase del vuelo de hasta 20 segundos produjo los siguientes parámetros para la regulación difusa:

- deltaMax = 0.056– desviación máxima;
- divMax = 0.0968 - la derivada máxima de la desviación;
- div2Max = 0.987 - la segunda derivada máxima de la desviación.

El proceso de transición después de la optimización se muestra en la Figura 9.

Las desviaciones a mayor escala se muestran en la Figura 10.

Figura 9a. El proceso de transición.

Figura 9b. Opciones de control.

Figura 10. Desviación de escala mayor del primer tramo del vuelo.

Los gráficos muestran que el sobreimpulso disminuyó y la desviación después del final del proceso de transición se volvió inferior a 0.005.

Para la optimización en la siguiente sección de vuelo, realizaremos la simulación con el estado guardado obtenido en la primera sección.

La simulación se lleva a cabo de 20 a 40 segundos de vuelo de misiles balísticos, la optimización se produce durante todo el proceso.

Como hemos completado el proceso de transición al comienzo de la segunda sección, llevamos a cabo la optimización solo por la desviación y el número de interruptores. El diagrama de bloques de optimización se muestra en la Figura 11.


Figura 11. Esquema de optimización para la segunda sección de vuelo.

La optimización automática para la segunda fase del vuelo de 20 a 40 segundos produjo los siguientes parámetros para la regulación difusa:

- deltaMax = 0.056– desviación máxima;
- divMax = 0.0974 - la derivada máxima de la desviación;
- div2Max = 0.980 - la segunda derivada máxima de la desviación.

Con los parámetros dados, la desviación del ángulo de inclinación respecto del dado disminuye durante toda la segunda sección del vuelo. Pero si usamos los parámetros obtenidos por la optimización en la segunda parte del vuelo para controlar hasta 66 segundos, entonces se puede ver que la precisión comienza a disminuir y la desviación comienza a aumentar después de 40 segundos (ver Fig. 12).


Figura 12. Proceso de control de misiles balísticos con ajustes optimizados para 20-40 segundos de vuelo.

Repita la optimización para el tercer tramo del vuelo. Guarde los resultados por 40 segundos.

Los usamos para comenzar y optimizar en una sección de 40 a 66 segundos.

La optimización automática para la última sección de vuelo de 40 a 66 segundos produjo los siguientes parámetros para la regulación difusa:

- deltaMax = 0.0146– desviación máxima;
- divMax = 0.0157– la derivada máxima de la desviación;
- div2Max = 0.555 - la segunda derivada máxima de la desviación.

El gráfico del proceso de control en la última sección del vuelo de misiles balísticos después de la optimización se muestra en la Figura 13.

Figura 13. Proceso de control de misiles balísticos en el último tramo del vuelo.

La Figura 13 muestra que con las nuevas configuraciones, la desviación en el intervalo de tiempo de vuelo de 40-66 segundos no aumenta, en contraste con las configuraciones optimizadas para el segundo segmento de vuelo (ver Fig. 12).

Por lo tanto, obtuvimos la configuración del controlador difuso para tres secciones del vuelo. Creemos un interruptor de modo que cambie la configuración del controlador durante el vuelo. El circuito del interruptor de modo se muestra en la Figura 14.


Figura 14. Interruptor de modo del controlador de misil balístico difuso.

Los modos de cambio tendrán lugar en el tiempo, en la parte superior un circuito lógico simple compara el tiempo actual del modelo con los puntos de cambio. Como resultado, se forma un vector de control de tres valores en el multiplexor. En este vector, el valor 1 está en la posición del intervalo de tiempo actual.

Los parámetros del controlador difuso calculados anteriormente mediante métodos de optimización se agrupan en vectores de tres valores.

Con la ayuda de un bloque de muestreo de tres valores, se selecciona uno que corresponde a 1 en el vector de control. Por lo tanto, cuando cambia el tiempo, los parámetros transferidos al controlador difuso cambian de acuerdo con la sección de vuelo actual.

Para mayor claridad, los valores transmitidos a través de la línea de comunicación se muestran en el diagrama. La figura corresponde a la última sección de un vuelo de misil balístico. El tiempo es más de 40 segundos. El vector de control (0, 0, 1) el último parámetro del conjunto se suministra al controlador.

En la Figura 15 se muestra el resultado de la simulación de controlar el ángulo de inclinación del cohete con el cambio de los parámetros del regulador.

Figura 15a. El proceso de transición.

Figura 15b. Opciones de control.

Conclusiones:
El método de optimización puede configurar un controlador basado en lógica difusa para que funcione en el modo de cambio de parámetros.

La desviación al trabajar con parámetros variables en el ejemplo dado disminuyó en 3-5 veces en comparación con la operación del controlador con parámetros constantes.

El archivo con proyectos para estudio independiente se puede descargar aquí ...