La esencia general de las clasificaciones de inserción es la siguiente:
- Itera sobre los elementos en la parte no ordenada de la matriz.
- Cada elemento se inserta en la parte ordenada de la matriz en el lugar donde debería estar.
Esto, en principio, es todo lo que necesita saber sobre la clasificación por insertos. Es decir, los tipos de inserción siempre dividen la matriz en 2 partes: ordenadas y sin clasificar. Cualquier elemento se recupera de la parte sin clasificar. Como la otra parte de la matriz está ordenada, puede encontrar rápidamente su lugar en esta matriz para este elemento extraído. El elemento se inserta donde sea necesario, como resultado de lo cual la parte ordenada de la matriz aumenta y la parte no clasificada disminuye. Eso es todo. Todo tipo de insertos funcionan según este principio.
El punto más débil de este enfoque es insertar un elemento en la parte ordenada de la matriz. De hecho, no es fácil y qué trucos no tienes que hacer para completar este paso.
Clasificación de inserción simple

Recorremos la matriz de izquierda a derecha y procesamos cada elemento por turnos. A la izquierda del siguiente elemento, aumentamos la parte ordenada de la matriz, a la derecha, a medida que avanza el proceso, la parte sin clasificar se evapora lentamente. En la parte ordenada de la matriz, se busca el punto de inserción para el siguiente elemento. El elemento en sí se envía al búfer, como resultado de lo cual aparece una celda vacía en la matriz; esto le permite desplazar los elementos y liberar el punto de inserción.
def insertion(data): for i in range(len(data)): j = i - 1 key = data[i] while data[j] > key and j >= 0: data[j + 1] = data[j] j -= 1 data[j + 1] = key return data
Utilizando inserciones simples como ejemplo, la principal ventaja de la mayoría (¡pero no de todas!) La clasificación por inserciones se ve de manera demostrativa, es decir, un procesamiento muy rápido de matrices casi ordenadas:

En este escenario, incluso la implementación más primitiva de las inserciones de clasificación probablemente superará al algoritmo súper optimizado para una clasificación rápida, incluso en matrices grandes.
Esto se ve facilitado por la idea principal de esta clase: la transferencia de elementos de la parte no ordenada de la matriz a la ordenada. Con una proximidad cercana de datos de magnitud similar, el punto de inserción generalmente se ubica cerca del borde de la parte ordenada, lo que le permite insertar con la menor sobrecarga.
No hay nada mejor para manejar matrices casi ordenadas que la ordenación por inserción. Cuando encuentra información en algún lugar donde la mejor complejidad de tiempo para ordenar por inserciones es
O ( n ) , lo más probable es que se refiera a situaciones con matrices casi ordenadas.
Ordenar por simples insertos de búsqueda binaria

Dado que el lugar para insertar se busca en la parte ordenada de la matriz, se sugiere la idea de utilizar una búsqueda binaria. Otra cosa es que la búsqueda del sitio de inserción no es crítica para la complejidad temporal del algoritmo (el principal consumidor de recursos es la etapa de insertar el elemento en la posición encontrada), por lo tanto, esta optimización hace poco.
Y en el caso de una matriz casi ordenada, una búsqueda binaria puede funcionar aún más lentamente, ya que comienza desde el medio de la sección ordenada, que, muy probablemente, estará demasiado lejos del punto de inserción (y tomará menos pasos para realizar una búsqueda normal desde la posición del elemento hasta el punto de inserción si los datos en la matriz como un todo ordenado).
def insertion_binary(data): for i in range(len(data)): key = data[i] lo, hi = 0, i - 1 while lo < hi: mid = lo + (hi - lo) // 2 if key < data[mid]: hi = mid else: lo = mid + 1 for j in range(i, lo + 1, -1): data[j] = data[j - 1] data[lo] = key return data
En defensa de la búsqueda binaria, noto que él puede decir la última palabra en la efectividad de otras clasificaciones por insertos. Gracias a él, en particular, los algoritmos como la clasificación de bibliotecarios y la clasificación de solitario van a la complejidad de tiempo promedio
O ( n log n ) . Pero sobre ellos más tarde.
Par ordenar por inserciones simples
Modificación de insertos simples, desarrollados en los laboratorios secretos de Oracle Corporation. Esta clasificación forma parte del JDK y forma parte del Quicksort de doble pivote. Se utiliza para ordenar matrices pequeñas (hasta 47 elementos) y ordenar áreas pequeñas de matrices grandes.

No se envían uno sino dos elementos adyacentes al búfer a la vez. Primero, se inserta el elemento más grande del par, e inmediatamente después, se aplica el método de inserción simple al elemento más pequeño del par.
Que da Ahorros por manejar un artículo más pequeño de un par. Para él, la búsqueda del punto de inserción y la inserción en sí se llevan a cabo solo en esa parte ordenada de la matriz, que no incluye el área ordenada utilizada para procesar un elemento más grande del par. Esto es posible porque los elementos más grandes y más pequeños se procesan inmediatamente uno tras otro en una pasada del bucle externo.
Esto no afecta la complejidad del tiempo promedio (todavía permanece igual a
O ( n 2 )), sin embargo, los insertos emparejados funcionan un poco más rápido que los habituales.
Ilustra los algoritmos en Python, pero aquí doy la fuente original (modificada para facilitar la lectura) en Java:
for (int k = left; ++left <= right; k = ++left) {
Tipo de concha

Este algoritmo tiene un enfoque muy ingenioso para determinar qué parte de la matriz se considera ordenada. En inserciones simples, todo es simple: desde el elemento actual, todo a la izquierda ya está ordenado, todo a la derecha aún no está ordenado. A diferencia de las inserciones simples, la ordenación de Shell no intenta formar inmediatamente una parte estrictamente ordenada de la matriz a la izquierda de un elemento. Crea una parte
casi ordenada de la matriz a la izquierda del elemento y lo hace lo suficientemente rápido.
La clasificación de shell arroja el elemento actual al búfer y lo compara con el lado izquierdo de la matriz. Si encuentra elementos más grandes a la izquierda, los desplaza a la derecha, dejando espacio para la inserción. Pero al mismo tiempo, no toma toda la parte izquierda, sino solo un cierto grupo de elementos, donde los elementos están separados entre sí por una cierta distancia. Dicho sistema le permite insertar rápidamente elementos en aproximadamente el área de la matriz donde deberían ubicarse.
Con cada iteración del bucle principal, esta distancia disminuye gradualmente y cuando se vuelve igual a uno, entonces la ordenación Shell en este momento se convierte en una ordenación clásica con inserciones simples, que se dieron al procesamiento de una matriz casi ordenada. Una ordenación de matriz casi ordenada se inserta en conversiones completamente ordenadas rápidamente.
def shell(data): inc = len(data) // 2 while inc: for i, el in enumerate(data): while i >= inc and data[i - inc] > el: data[i] = data[i - inc] i -= inc data[i] = el inc = 1 if inc == 2 else int(inc * 5.0 / 11) return data
La clasificación de peine por un principio similar mejora la clasificación de burbujas, por lo que la complejidad temporal del algoritmo con
O ( n 2 ) salta hasta
O ( n log n ) . Por desgracia, Shell no logra repetir esta hazaña: la mejor complejidad de tiempo llega a
O ( n log 2 n ) .
Se han escrito varios habrastati sobre la clasificación de Shell, por lo que no seremos sobrecargados de información y seguiremos adelante.
Clasificación de árboles
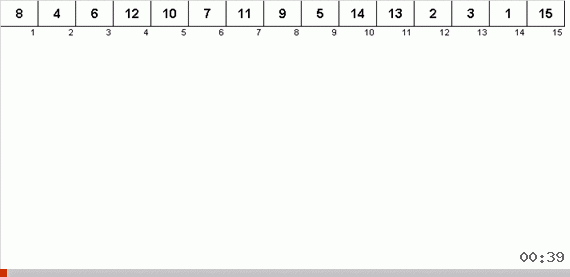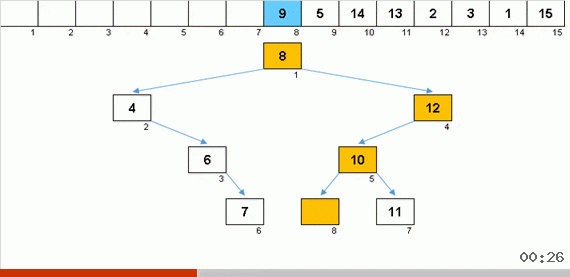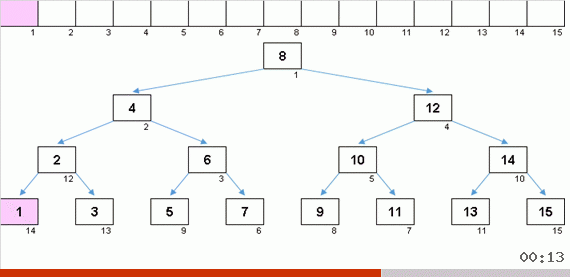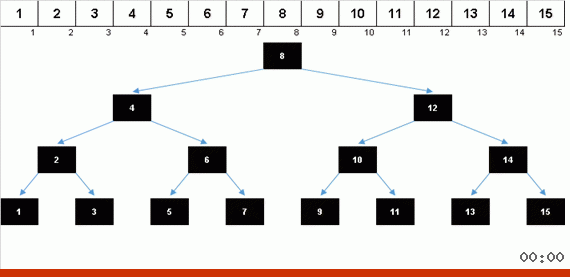
Ordenar con un árbol debido a memoria adicional resuelve rápidamente el problema de agregar otro elemento a la parte ordenada de la matriz. Además, el árbol binario actúa como la parte ordenada de la matriz. Un árbol se forma literalmente sobre la marcha al iterar sobre los elementos.
El elemento se compara primero con la raíz, y luego con más nodos anidados de acuerdo con el principio: si el elemento es más pequeño que el nodo, entonces descendemos por la rama izquierda, si no menos, entonces la derecha. Un árbol construido por dicha regla puede ser fácilmente burlado para pasar de nodos con valores más bajos a nodos con valores más grandes (y así obtener todos los elementos en orden creciente).
Aquí se resuelve el inconveniente principal de ordenar por inserciones (el costo de insertar un elemento en su lugar en la parte ordenada de la matriz), la construcción avanza bastante rápido. En cualquier caso, para liberar el punto de inserción, no es necesario mover lentamente las caravanas de los elementos como en los algoritmos anteriores. Parece que aquí está, el mejor de los insertos de clasificación. Pero hay un problema.
Cuando obtienes un hermoso árbol de Navidad simétrico (el llamado árbol perfectamente equilibrado) como en la animación de los tres párrafos anteriores, la inserción ocurre rápidamente, porque el árbol en este caso tiene los niveles de anidación más bajos posibles. Pero rara vez se obtiene una estructura equilibrada (o al menos cercana a eso) de una matriz aleatoria. Y el árbol, muy probablemente, será imperfecto y desequilibrado, con distorsiones, un horizonte lleno de basura y un número excesivo de niveles.
Una matriz aleatoria con valores del 1 al 10. Los elementos en este orden generan un árbol binario no balanceado: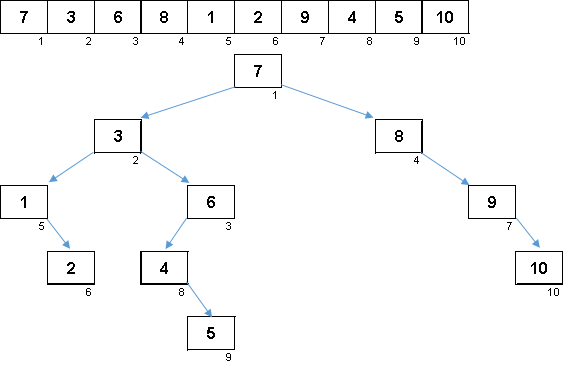
Un árbol no es suficiente para construir, aún necesita ser burlado. Cuanto más desequilibrio, más fuerte se deslizará el algoritmo transversal del árbol. Aquí, como dicen las estrellas, una matriz aleatoria puede generar tanto un inconveniente feo (que es más probable) como un fractal similar a un árbol.
Los valores de los elementos son los mismos, pero el orden es diferente. Se genera un árbol binario equilibrado: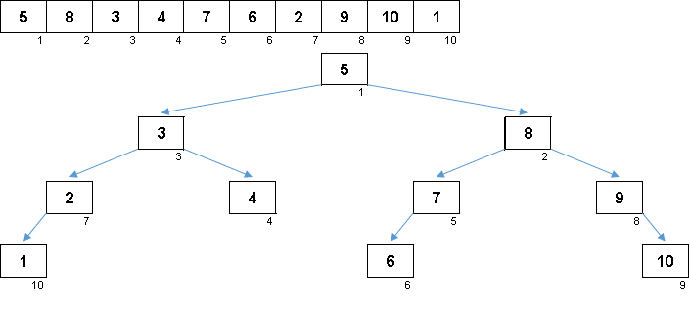
 En hermosa sakura
En hermosa sakura
No hay suficiente pétalo:
Un árbol binario de docenas.El problema de los árboles desequilibrados se resuelve mediante la ordenación por inversión, que utiliza un tipo especial de árbol de búsqueda binario: árbol de reproducción. Este es un árbol transformador maravilloso, que después de cada operación se reconstruye en un estado equilibrado. Sobre esto será un artículo separado. Para entonces, prepararé las implementaciones de Python para Tree Sort y Splay sort.
Bueno, bueno, revisamos brevemente los insertos de clasificación más populares. Inserciones simples, concha y árbol binario que todos conocemos desde la escuela. Ahora considere otros representantes de esta clase, no tan conocidos.
Wiki / wiki -
Inserciones / configuración de inserción , Shell / de Shell , Árbol / ÁrbolArtículos de la serie:
Quién usa AlgoLab: recomiendo actualizar el archivo. Agregué insertos de búsqueda binarios simples e insertos emparejados a esta aplicación. También reescribió completamente la visualización para Shell (en la versión anterior no había nada que entender) y agregó resaltado a la rama principal al insertar un elemento en el árbol binario.