Redes neuronales, principios fundamentales de funcionamiento, diversidad y topología.

Las redes neuronales han revolucionado el campo del reconocimiento de patrones, pero debido a la interpretación no obvia del principio de funcionamiento, no se utilizan en áreas como la medicina y la evaluación de riesgos. Requiere una representación visual de la red, lo que hará que no sea una caja negra, sino al menos "translúcida". Cristopher Olah, en Redes neuronales, colectores y topología, demostró los principios del funcionamiento de la red neuronal y los conectó con la teoría matemática de la topología y la diversidad, que sirvió de base para este artículo. Para demostrar el funcionamiento de una red neuronal, se utilizan redes neuronales profundas de baja dimensión.

Comprender el comportamiento de las redes neuronales profundas generalmente no es una tarea trivial. Es más fácil explorar redes neuronales profundas de baja dimensión, redes en las que solo hay unas pocas neuronas en cada capa. Para redes de baja dimensión, puede crear visualizaciones para comprender el comportamiento y la capacitación de dichas redes. Esta perspectiva proporcionará una comprensión más profunda del comportamiento de las redes neuronales y observará la conexión que combina las redes neuronales con un campo de las matemáticas llamado topología.

De esto se desprenden varias cosas interesantes, incluidos los límites inferiores fundamentales sobre la complejidad de una red neuronal capaz de clasificar ciertos conjuntos de datos.

Considere el principio de la red usando un ejemplo

Comencemos con un conjunto de datos simple: dos curvas en un plano. La tarea de red aprenderá a clasificar los puntos que pertenecen a las curvas.



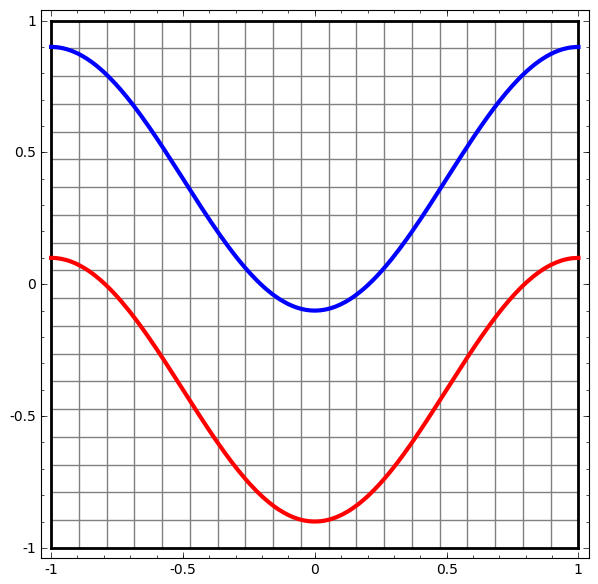
Una forma obvia de visualizar el comportamiento de una red neuronal, para ver cómo el algoritmo clasifica todos los objetos posibles (en nuestro ejemplo, puntos) de un conjunto de datos.

Comencemos con la clase más simple de red neuronal, con una capa de entrada y salida. Dicha red intenta separar dos clases de datos dividiéndolos por una línea.



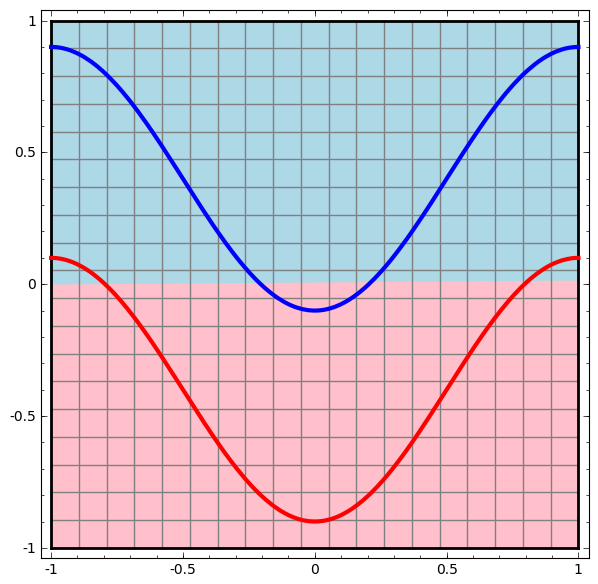
Tal red no se usa en la práctica. Las redes neuronales modernas generalmente tienen varias capas entre su entrada y salida, llamadas capas "ocultas".

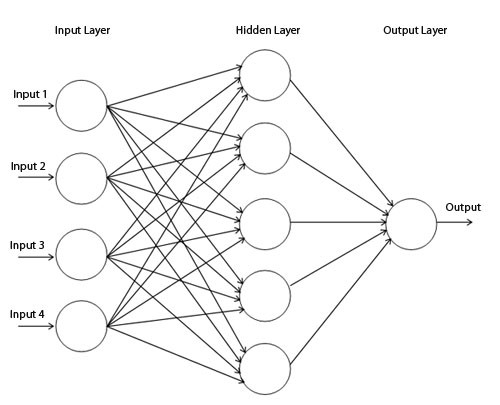
Diagrama de red simple

Visualizamos el comportamiento de esta red, observando lo que hace con diferentes puntos en su campo. Una red de capa oculta separa los datos de una curva más compleja que una línea.



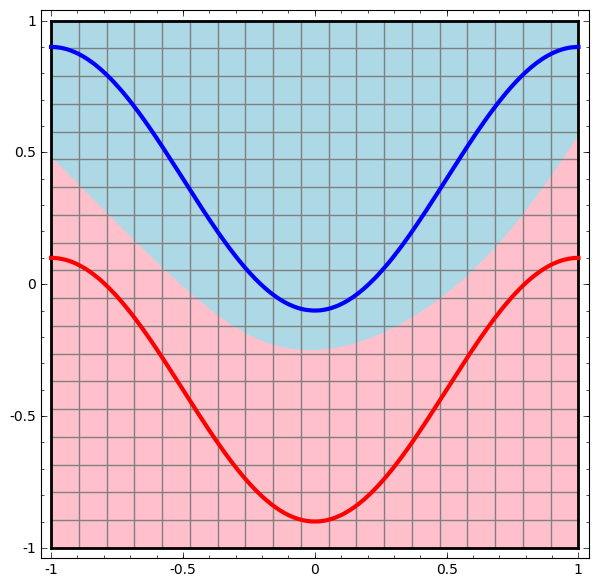
Con cada capa, la red transforma los datos, creando una nueva vista. Podemos ver los datos en cada una de estas vistas y cómo la red con una capa oculta los clasifica. Cuando el algoritmo llega a la presentación final, la red neuronal dibujará una línea a través de los datos (o en dimensiones más altas, un hiperplano).

En la visualización anterior, se consideran los datos en una vista sin procesar. Puedes imaginar esto mirando la capa de entrada. Ahora, considérelo después de convertirlo a la primera capa. Puedes imaginar esto mirando la capa oculta.
Cada medida corresponde a la activación de una neurona en la capa.



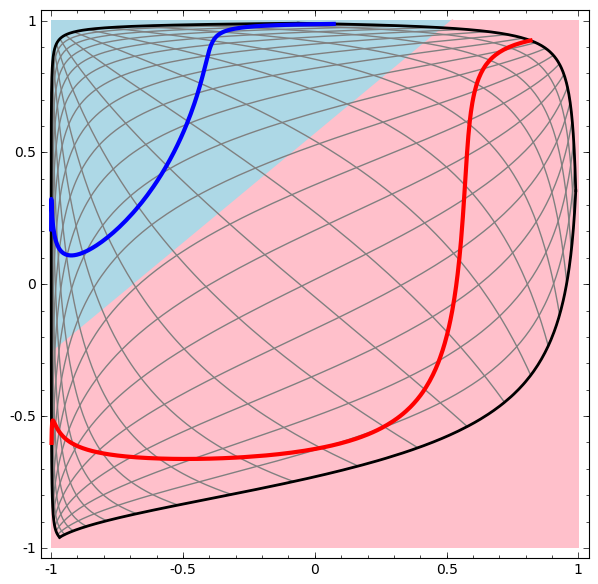
La capa oculta se entrena en la vista para que los datos sean linealmente separables.

Representación continua de capas

En el enfoque descrito en la sección anterior, aprendemos a comprender las redes al observar la presentación correspondiente a cada capa. Esto nos da una lista discreta de puntos de vista.

La parte no trivial es comprender cómo nos movemos de uno a otro. Afortunadamente, los niveles de la red neuronal tienen propiedades que lo hacen posible.
Hay muchos tipos diferentes de capas usadas en redes neuronales.

Considere una capa de tanh para un ejemplo específico. Tanh-tanh-layer (Wx + b) consta de:

1. La transformación lineal de la matriz de "peso" W
2. Traducción usando el vector b
3. Aplicación puntual de tanh.

Podemos representar esto como una transformación continua de la siguiente manera:



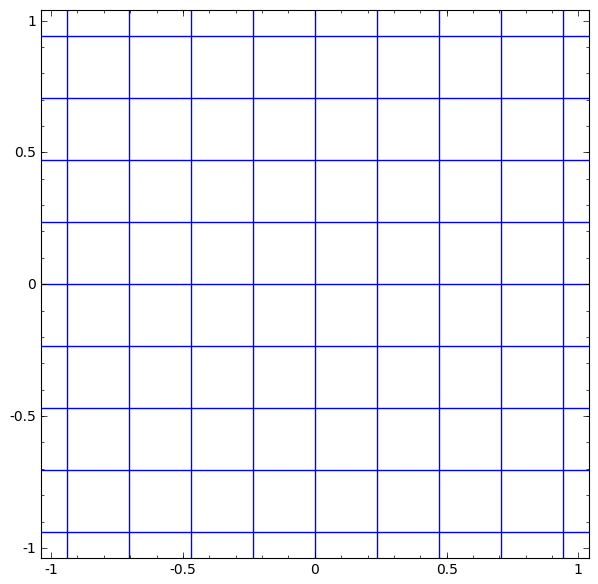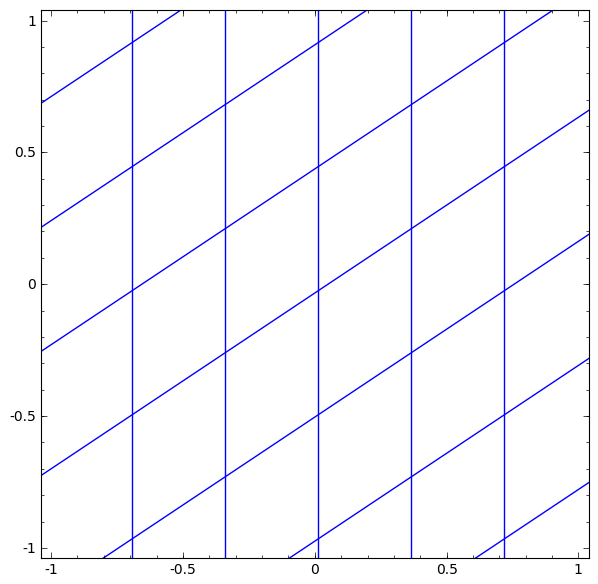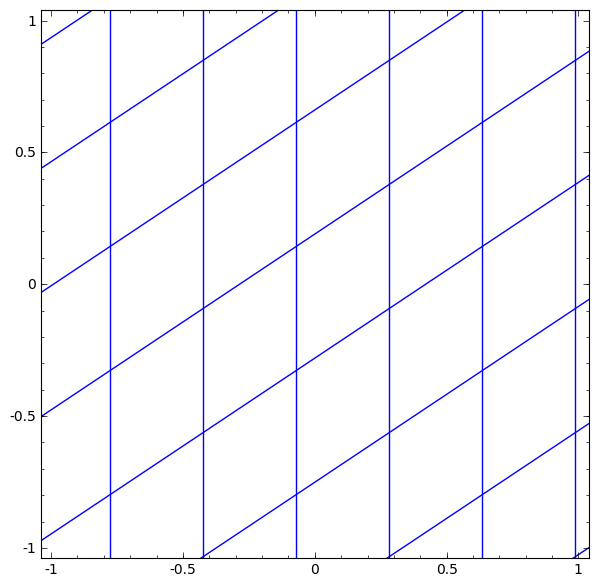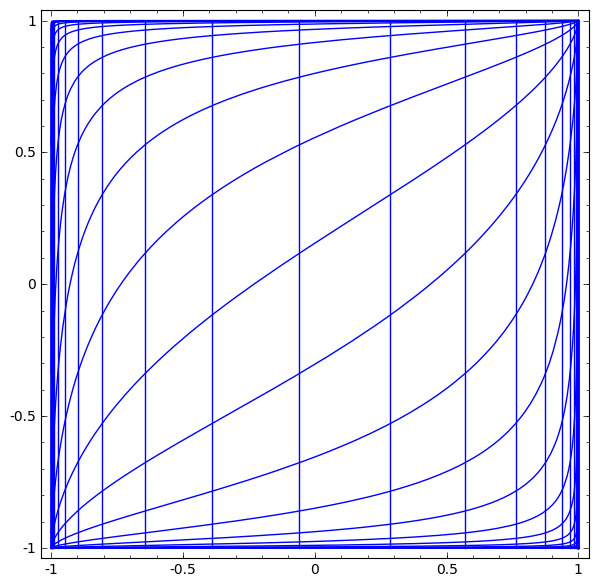
Este principio de funcionamiento es muy similar a otras capas estándar que consisten en una transformación afín, seguida de la aplicación puntual de una función de activación monotónica.
Este método puede usarse para comprender redes más complejas. Entonces, la siguiente red clasifica dos espirales que están ligeramente enredadas usando cuatro capas ocultas. Con el tiempo, se puede ver que la red neuronal se mueve desde una vista sin procesar a un nivel superior que la red ha estudiado para clasificar los datos. Si bien las espirales se enredan inicialmente, hacia el final son linealmente separables.



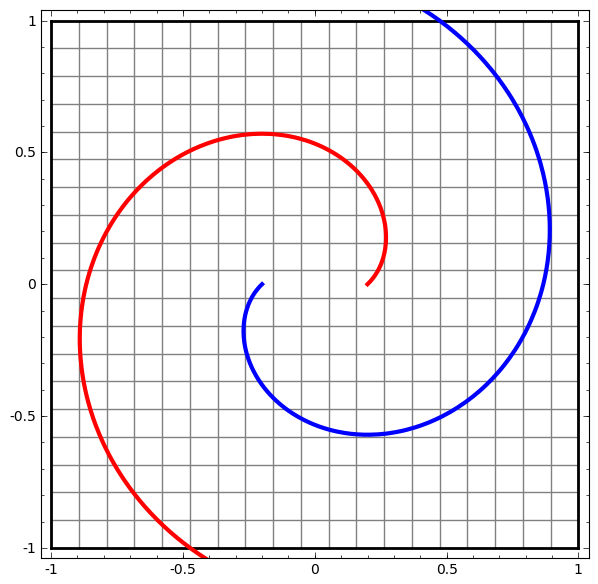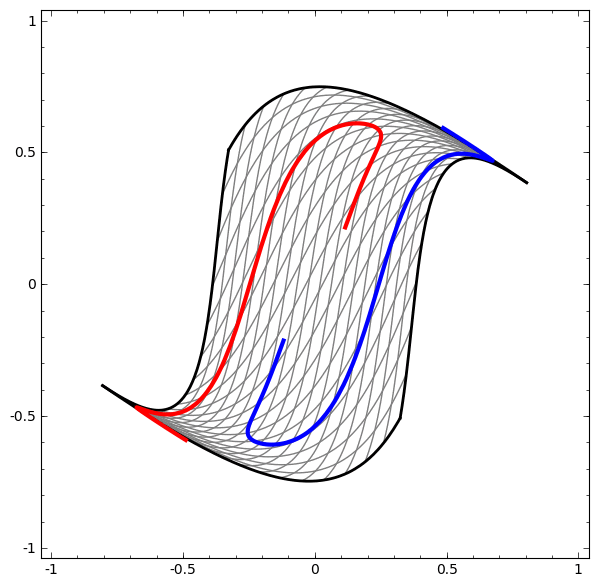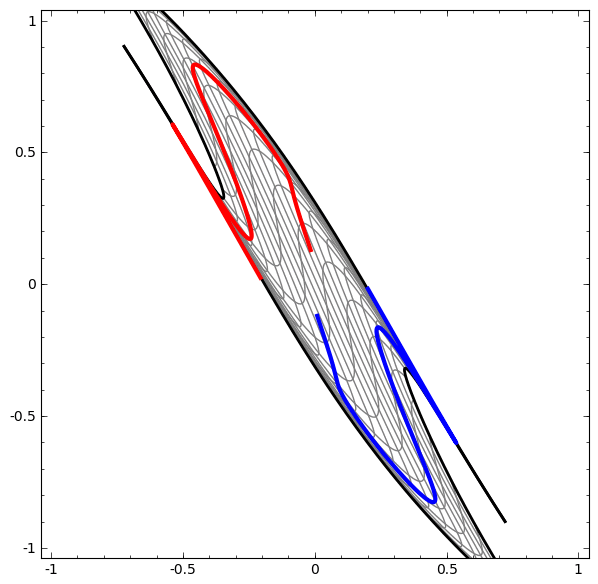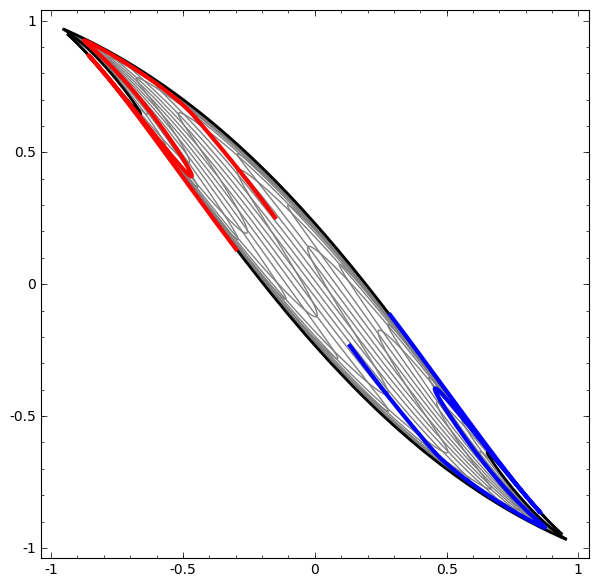
Por otro lado, la siguiente red, que también usa varios niveles, pero no puede clasificar dos espirales, que están más enredados.



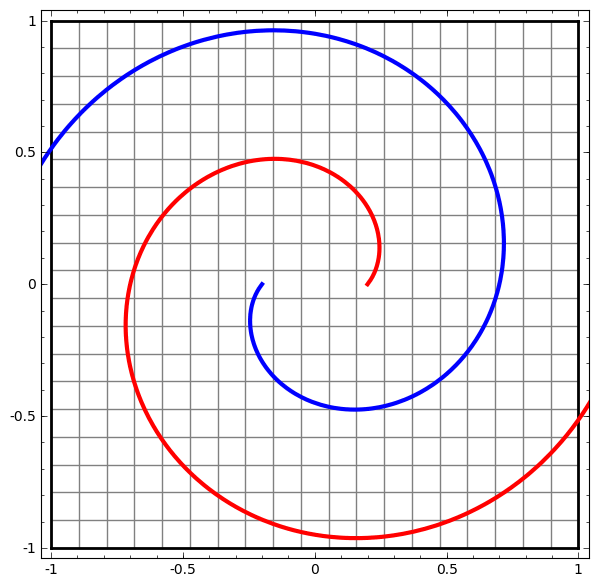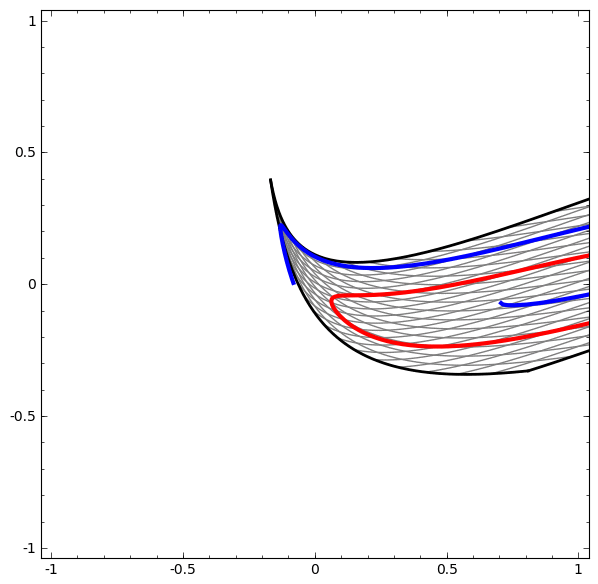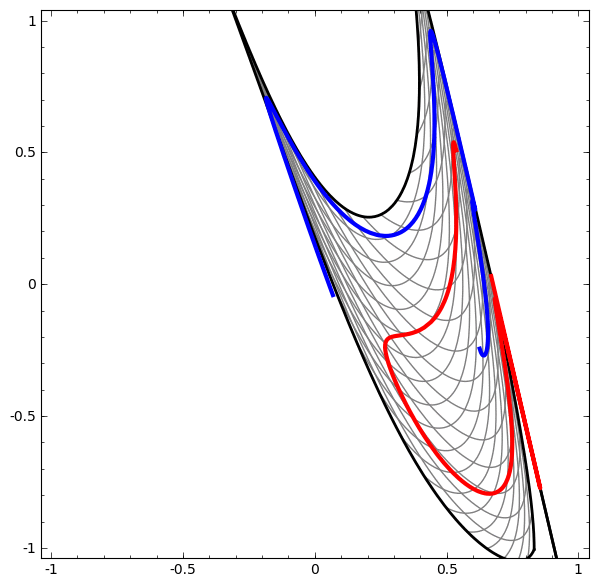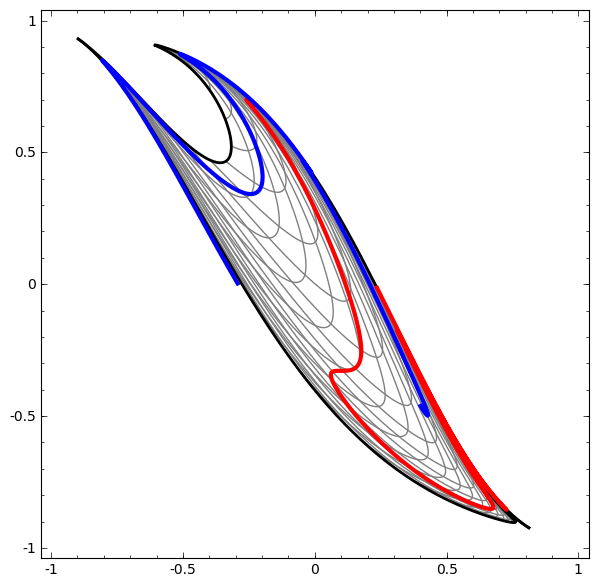
Cabe señalar que estas tareas tienen una complejidad limitada, porque se utilizan redes neuronales de baja dimensión. Si se utilizaron redes más amplias, la resolución de problemas se simplificó.

Capas Tang

Cada capa estira y comprime el espacio, pero nunca corta, no se rompe y no lo dobla. Intuitivamente, vemos que las propiedades topológicas se conservan en cada capa.

Tales transformaciones que no afectan la topología se denominan homomorfismos (Wiki - Este es un mapeo del sistema algebraico A que preserva las operaciones básicas y las relaciones básicas). Formalmente, son biyecciones que son funciones continuas en ambas direcciones. En una asignación biyectiva, cada elemento de un conjunto corresponde exactamente a un elemento de otro conjunto, y se define una asignación inversa que tiene la misma propiedad.

El teorema

Las capas con N entradas y N salidas son homomorfismos si la matriz de peso W no está degenerada. (Debe tener cuidado con el dominio y el rango).

Topología y clasificación.

Considere un conjunto de datos bidimensionales con dos clases A, B⊂R2:

A = {x | d (x, 0) <1/3}

B = {x | 2/3 <d (x, 0) <1}



A rojo, B azul

Requisito: una red neuronal no puede clasificar este conjunto de datos sin 3 o más capas ocultas, independientemente del ancho.

Como se mencionó anteriormente, la clasificación con una función sigmoidea o capa softmax es equivalente a tratar de encontrar el hiperplano (o en este caso la línea) que separa A y B en la representación final. Con solo dos capas ocultas, la red es topológicamente incapaz de compartir datos de esta manera, y está condenada al fracaso en este conjunto de datos.
En la siguiente visualización, observamos una vista latente mientras la red está entrenando junto con la línea de clasificación.



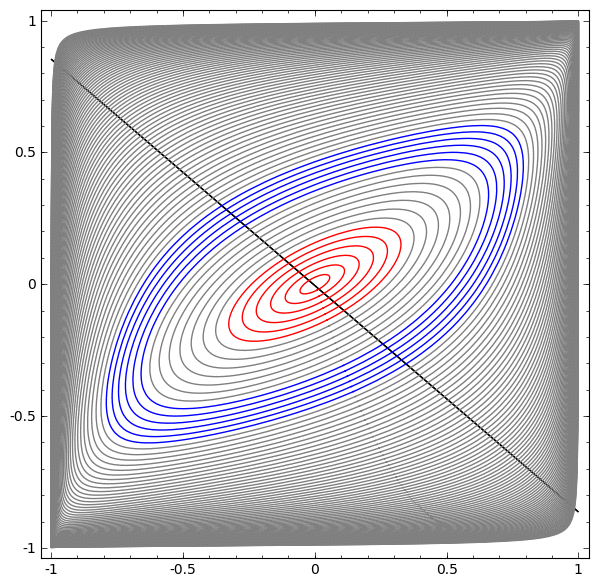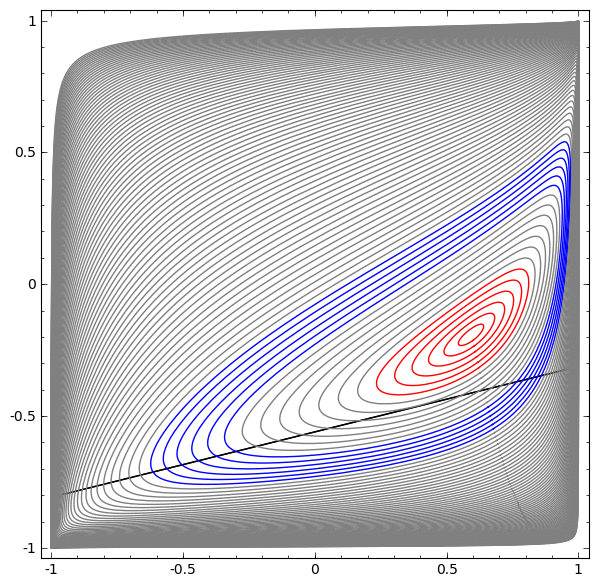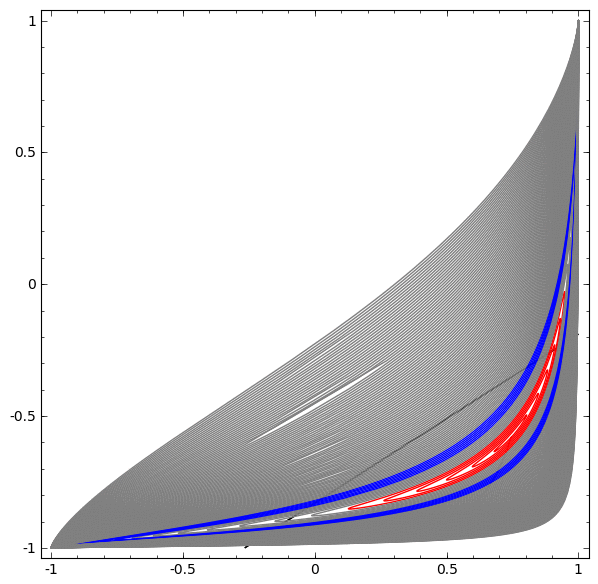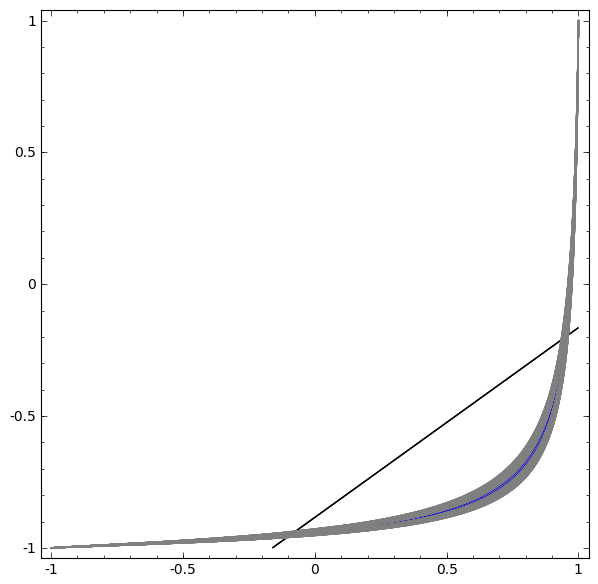
Para esta red de capacitación no es suficiente para lograr un resultado cien por ciento.
El algoritmo cae en un mínimo local no productivo, pero puede lograr una precisión de clasificación de ~ 80%.

En este ejemplo, solo había una capa oculta, pero no funcionó.
Declaración O cada capa es un homomorfismo, o la matriz de peso de la capa tiene determinante 0.


Si agregamos un tercer elemento oculto, el problema se volverá trivial. La red neuronal reconoce la siguiente representación:



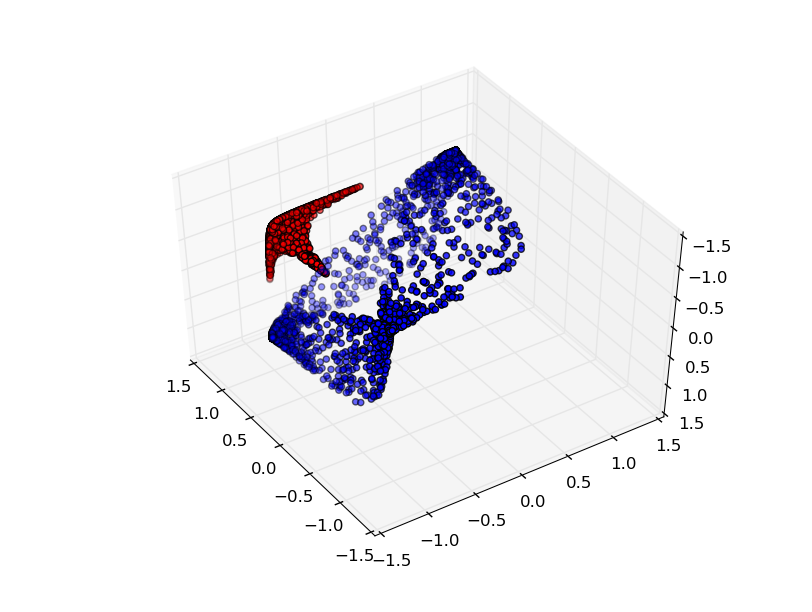
La vista permite separar conjuntos de datos con un hiperplano.
Para comprender mejor lo que está sucediendo, veamos un conjunto de datos aún más simple, que es unidimensional:



A = [- 1 / 3,1 / 3]
B = [- 1, −2 / 3] ∪ [2 / 3,1]
Sin usar una capa de dos o más elementos ocultos, no podemos clasificar este conjunto de datos. Pero, si usamos una red con dos elementos, aprenderemos cómo representar los datos como una buena curva que nos permite separar las clases usando una línea:



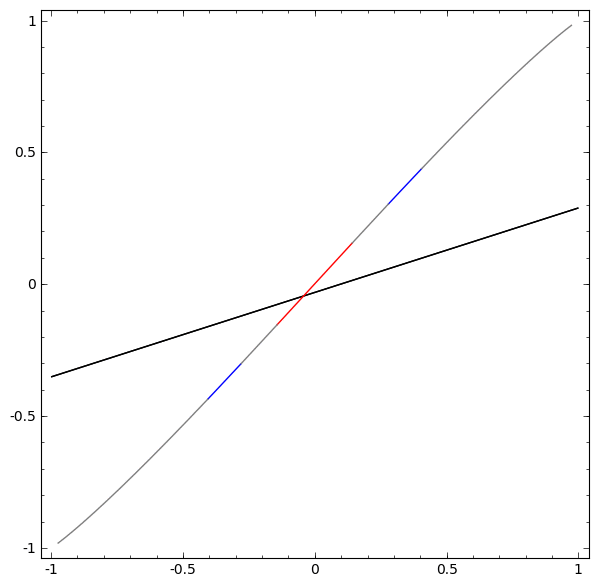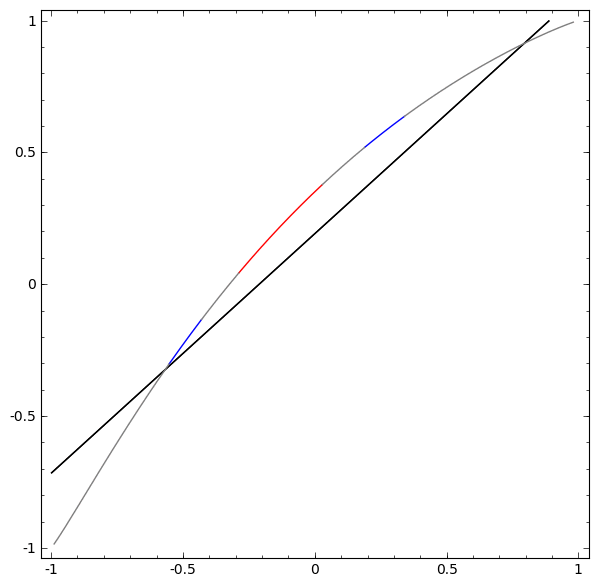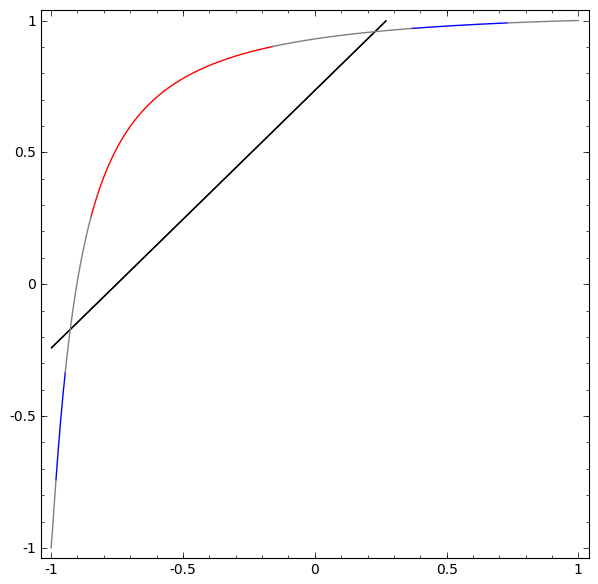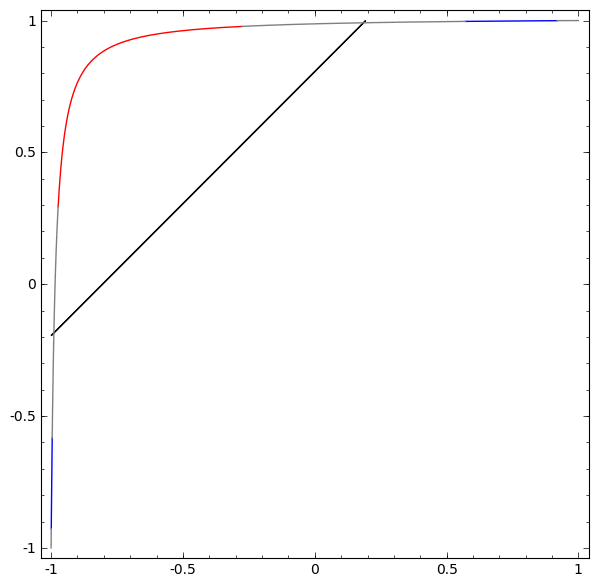
Que esta pasando Un elemento oculto aprende a disparar cuando x> -1/2, y uno aprende a disparar cuando x> 1/2. Cuando se activa el primero, pero no el segundo, sabemos que estamos en A.

Conjetura de la variedad

¿Se aplica esto a los conjuntos de datos del mundo real, como los conjuntos de imágenes? Si te tomas en serio la hipótesis de la diversidad, creo que es importante.

La hipótesis multidimensional es que los datos naturales forman múltiples de baja dimensión en el espacio de implantación. Hay razones teóricas [1] y experimentales [2] para creer que esto es cierto. Si es así, entonces la tarea del algoritmo de clasificación es separar el paquete de múltiples enredados.

En los ejemplos anteriores, una clase rodeaba completamente a la otra. Sin embargo, es poco probable que la variedad de imágenes de perros esté completamente rodeada por una colección de imágenes de gatos. Pero hay otras situaciones topológicas más plausibles que aún pueden surgir, como veremos en la siguiente sección.

Conexiones y homotopías

Otro conjunto de datos interesante son los dos toros conectados A y B.



Al igual que los conjuntos de datos anteriores que examinamos, este conjunto de datos no se puede dividir sin usar n + 1 dimensiones, es decir, la cuarta dimensión.

Las conexiones se estudian en la teoría de los nudos, en el campo de la topología. A veces, cuando vemos una conexión, no está claro de inmediato si es incoherencia (muchas cosas que se enredan pero que pueden separarse por deformación continua) o no.



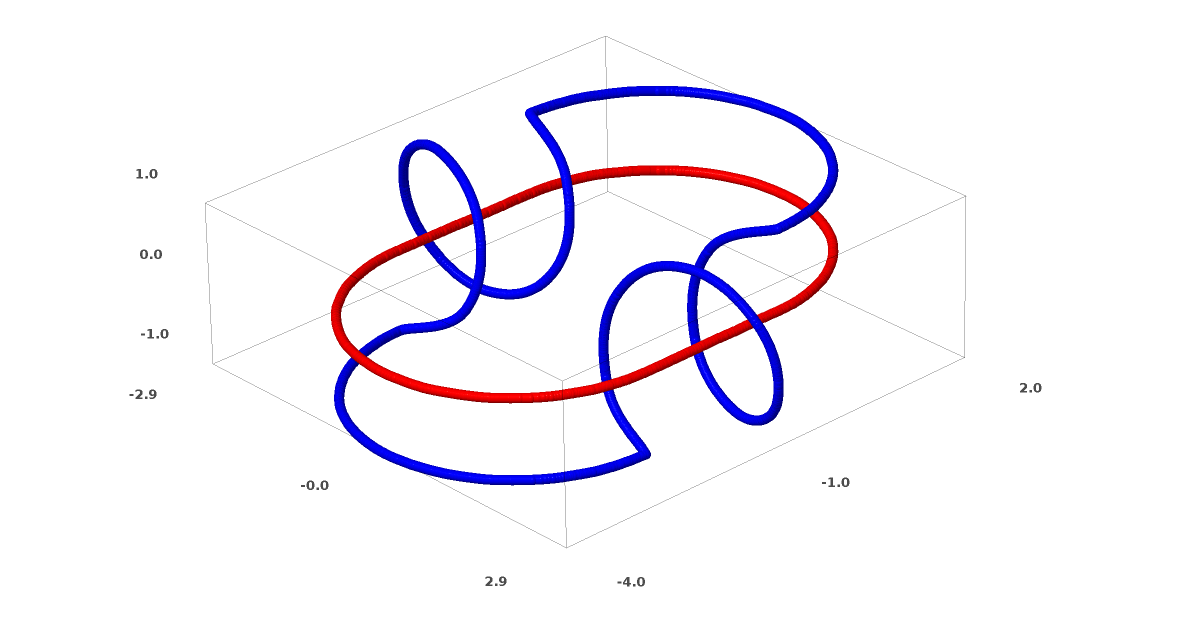
Incoherencia relativamente simple.

Si una red neuronal que usa capas con solo tres unidades puede clasificarla, entonces es incoherente. (Pregunta: ¿Pueden teóricamente clasificarse todas las incoherencias en la red con solo tres incoherencias?)

Desde el punto de vista de este nodo, la visualización continua de representaciones creadas por una red neuronal es un procedimiento para desentrañar conexiones. En topología, llamaremos a esta isotopía ambiental entre el enlace original y los separados.

Formalmente, la isotopía del espacio circundante entre los colectores A y B es una función continua F: [0,1] × X → Y, de modo que cada Ft es un homeomorfismo de X a su rango, F0 es una función de identidad y F1 asigna A a B. T .e. Ft va continuamente del mapa A a sí mismo, al mapa A a B.

Teorema: hay una isotopía del espacio circundante entre la entrada y la representación del nivel de red si: a) W no está degenerado, b) estamos listos para transferir neuronas a la capa oculta yc) hay más de 1 elemento oculto.


Hasta ahora, es poco probable que las relaciones de las que hablamos aparezcan en datos reales, pero hay generalizaciones de un nivel superior. Es plausible que tales características puedan existir en datos reales.

Las conexiones y los nodos son múltiples unidimensionales, pero necesitamos 4 dimensiones para que las redes puedan desentrañarlos a todos. De manera similar, se puede requerir un espacio dimensional aún mayor para poder expandir múltiples n-dimensionales. Todos los colectores n-dimensionales se pueden expandir en 2n + 2 dimensiones. [3]

Salida fácil

La manera más fácil es tratar de separar los colectores y estirar las partes que estén lo más enredadas posible. Aunque esto no estará cerca de una solución genuina, dicha solución puede lograr una precisión de clasificación relativamente alta y ser un mínimo local aceptable.



Tales mínimos locales son absolutamente inútiles en términos de tratar de resolver problemas topológicos, pero los problemas topológicos pueden proporcionar una buena motivación para estudiar estos problemas.

Por otro lado, si solo estamos interesados ​​en lograr buenos resultados de clasificación, el enfoque es aceptable. Si una pequeña cantidad de una variedad de datos queda atrapada en otra variedad, ¿es esto un problema? Es probable que sea posible obtener resultados de clasificación arbitrariamente buenos, a pesar de este problema.

¿Capas mejoradas para manipular múltiples?

Es difícil imaginar que las capas estándar con transformaciones afines sean realmente buenas para manipular múltiples.

¿Quizás tiene sentido tener una capa completamente diferente, que podemos usar en la composición con otras más tradicionales?

El estudio de un campo vectorial con una dirección en la que queremos cambiar la variedad es prometedor:



Y luego deformamos el espacio en función del campo vectorial:



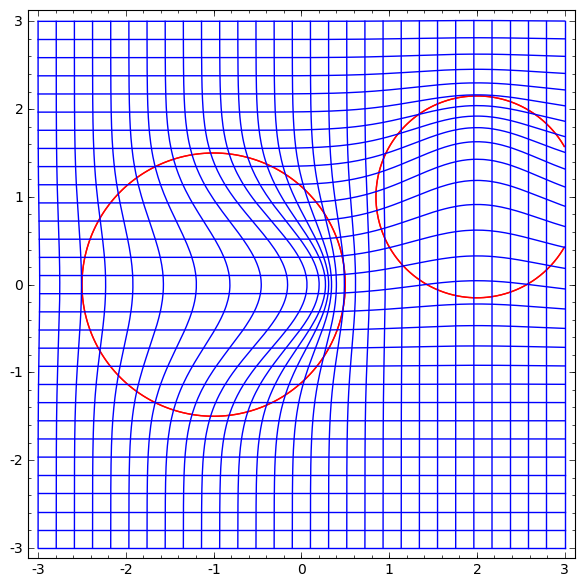
Se podría estudiar el campo vectorial en puntos fijos (solo tomar algunos puntos fijos del conjunto de datos de prueba para usar como anclajes) e interpolar de alguna manera.


Donde v0 y v1 son vectores, y f0 (x) y f1 (x) son gaussianos n-dimensionales.

K-Capas vecinas más cercanas

La separabilidad lineal puede ser una necesidad enorme y posiblemente irrazonable de redes neuronales. Es natural utilizar el método k-vecinos más cercanos (k-NN). Sin embargo, el éxito de k-NN depende en gran medida de la presentación que clasifica, por lo que se requiere una buena presentación antes de que k-NN pueda funcionar bien.

k-NN es diferenciable con respecto a la representación sobre la que actúa. De esta manera, podemos entrenar directamente a la red para clasificar k-NN. Esto puede verse como un tipo de capa de "vecino más cercano" que actúa como una alternativa a softmax.
No queremos advertir con todo nuestro conjunto de entrenamiento para cada mini-fiesta, porque será un procedimiento muy costoso. El enfoque adaptado consiste en clasificar cada elemento del mini lote en función de las clases de los otros elementos del mini lote, dando a cada unidad de peso dividido por la distancia desde el objetivo de clasificación.

Desafortunadamente, incluso con arquitecturas complejas, el uso de k-NN reduce la probabilidad de error, y el uso de arquitecturas más simples degrada los resultados.

Conclusión

Las propiedades topológicas de los datos, como las relaciones, pueden hacer imposible la división lineal de clases usando redes de baja dimensión, independientemente de la profundidad. Incluso en casos donde es técnicamente posible. Por ejemplo, espirales, que pueden ser muy difíciles de separar.

Para una clasificación de datos precisa, las redes neuronales necesitan capas anchas. Además, las capas tradicionales de la red neuronal son poco adecuadas para representar manipulaciones importantes con múltiples; incluso si establecemos los pesos manualmente, sería difícil representar de forma compacta las transformaciones que queremos.