Aprende OpenGL. Lección 5.6 - Mapeo de paralaje

Mapeo de paralaje

La técnica de texturizado de Mapeo de paralaje es algo similar en efecto al Mapeo normal , pero se basa en un principio diferente. La similitud es que, al igual que el mapeo normal, esta técnica aumenta significativamente la complejidad visual y los detalles de la superficie con la textura aplicada al mismo tiempo creando una ilusión plausible de la presencia de diferencias de altura en la superficie. Parallax Mapping funciona muy bien en combinación con Normal Mapping para crear resultados muy confiables: la técnica descrita transmite el efecto de alivio mucho mejor que Normal Mapping, y Normal Mapping lo complementa para una simulación plausible de iluminación dinámica. El mapeo de paralaje difícilmente puede considerarse una técnica directamente relacionada con los métodos de simulación de iluminación, pero elegí esta sección para considerarlo, ya que el método es un desarrollo lógico de las ideas del mapeo normal. También noto que para analizar este artículo, se requiere una buena comprensión del algoritmo de Mapeo Normal, especialmente el concepto de espacio tangente o espacio tangente .


El mapeo de paralaje pertenece a la familia de mapeo de desplazamiento o técnicas de textura en relieve que compensan los vértices de una geometría en función de los valores almacenados en los mapas de textura especiales. Por ejemplo, imagine un plano compuesto del orden de mil vértices. Cada uno de ellos puede desplazarse según el valor leído de la textura, que representa la altura del plano en un punto dado. Dicha textura, que contiene los valores de altura en cada texel, se denomina mapa de altura . Un ejemplo de dicho mapa, obtenido sobre la base de las características geométricas de la superficie del ladrillo, es la siguiente imagen:


Al tomar muestras de este mapa y cambiar cada vértice de acuerdo con el valor de altura, es posible obtener una superficie convexa a partir de un plano ideal que repite los parámetros geométricos de la superficie original. Entonces, tomando un plano con un número suficiente de vértices y aplicando un mapa de altura del ejemplo, puede obtener el siguiente resultado:


El enfoque descrito es simple y fácil de implementar, pero requiere una alta densidad de vértices en el objeto procesado, de lo contrario, el resultado del cambio será demasiado grueso. Y si en cada superficie plana comenzamos a liberar mil vértices o más, entonces muy pronto simplemente no tendremos tiempo para procesar todo lo que necesitamos. ¿Quizás haya un algoritmo que le permita simular cualitativamente la calidad del ingenuo algoritmo de Mapeo de desplazamiento, pero sin requerir tales costos de geometría? Si te paras, siéntate, ¡porque en la imagen de arriba solo hay seis vértices (dos triángulos)! El relieve del ladrillo se imita perfectamente gracias al uso de Mapeo de paralaje, una técnica de textura de relieve que no requiere muchos vértices para transmitir fielmente el relieve de la superficie, pero, como el Mapeo normal, que utiliza un enfoque original para engañar a los ojos del observador.

La idea principal de la implementación es distorsionar las coordenadas de textura para el fragmento actual en función de la dirección de la mirada y los datos del mapa de altura para crear la ilusión de que este fragmento pertenece a una parte de la superficie que se encuentra más arriba o más abajo de lo que realmente es. Para una mejor comprensión del principio, mire el diagrama de nuestro ejemplo con ladrillos:

Aquí, la línea roja aproximada representa los valores del mapa de altura, reflejando las características geométricas de la superficie de mampostería simulada. Vector $$$\ color {orange} {\ bar {V}}$ representa la dirección desde la superficie hasta el observador ( viewDir ). Si el avión estuviera realmente en relieve, entonces el observador vería un punto en la superficie $$$\ color {azul} B$ . Sin embargo, de hecho tenemos un plano ideal y el rayo en la dirección de la vista cruza el plano en un punto $$$\ color {verde} A$ Eso es obvio. Tarea de mapeo de paralaje para cambiar las coordenadas de textura en un punto $$$\ color {verde} A$ para que se vuelvan idénticas a las coordenadas correspondientes al punto $$$\ color {azul} B$ . Además para el fragmento actual (corresponde al punto $$$\ color {verde} A$ ) usamos las coordenadas obtenidas del punto $$$\ color {azul} B$ el muestreo de textura es necesario para todos, lo que crea la ilusión de que el observador ve un punto $$$\ color {azul} B$ .

La principal dificultad radica en cómo calcular las coordenadas de textura de un punto $$$\ color {azul} B$ estar en el punto $$$\ color {verde} A$ . Parallax Mapping ofrece una solución aproximada usando una escala simple del vector de dirección desde la superficie $$$\ color {orange} {\ bar {V}}$ al observador por la altura del fragmento $$$\ color {verde} A$ . Es decir solo cambia la longitud $$$\ color {orange} {\ bar {V}}$ para que coincida con el tamaño de la muestra del mapa de altura $$$\ color {verde} {H (A)}$ correspondiente al fragmento $$$\ color {verde} A$ . El siguiente diagrama muestra el resultado de la escala - vector $$$\ color {marrón} {\ bar {P}}$ :


Luego, el vector resultante $$$\ color {marrón} {\ bar {P}}$ descompuesto en componentes de acuerdo con el sistema de coordenadas del plano en sí, que se utilizan como compensaciones para las coordenadas de textura originales. Además, desde el vector $$$\ color {marrón} {\ bar {P}}$ se calcula utilizando el valor del mapa de altura, cuanto más corresponda el valor de altura al fragmento actual, más fuerte será el desplazamiento para él.

Esta técnica simple da buenos resultados en algunos casos, pero sigue siendo una estimación muy aproximada de la posición de un punto. $$$\ color {azul} B$ . Si el mapa de altura contiene áreas con valores que cambian bruscamente, el resultado del desplazamiento se vuelve incorrecto: lo más probable es que el vector $$$\ color {marrón} {\ bar {P}}$ incluso cerca no caerá en las proximidades del punto $$$\ color {azul} B$ :

Basado en lo anterior, queda otra pregunta: cómo determinar cómo proyectar correctamente un vector $$$\ color {marrón} {\ bar {P}}$ a una superficie orientada arbitrariamente para obtener componentes para compensar las coordenadas de textura? Sería bueno realizar cálculos en un determinado sistema de coordenadas, donde la expansión del vector $$$\ color {marrón} {\ bar {P}}$ en los componentes x e y siempre corresponderían a la base del sistema de coordenadas de textura. Si trabajó cuidadosamente la lección sobre Mapeo Normal , entonces ya adivinó que estamos hablando de cálculos en el espacio tangente.

Transferencia del vector de la superficie al observador $$$\ color {orange} {\ bar {V}}$ en el espacio tangente obtenemos un vector modificado $$$\ color {marrón} {\ bar {P}}$ , cuya descomposición de componentes siempre se llevará a cabo de acuerdo con los vectores tangente y bi-tangente para una superficie dada. Dado que la tangente y la bi-tangente siempre están alineadas con los ejes del sistema de coordenadas de textura de la superficie, entonces, independientemente de la orientación de la superficie, puede usar con seguridad los componentes x e y del vector $$$\ color {marrón} {\ bar {P}}$ como compensaciones para las coordenadas de textura.

Sin embargo, la teoría es suficiente y, después de remangarnos, pasamos a la implementación inmediata.

Mapeo de paralaje

Para la implementación, usaremos un plano simple con tangentes y tangentes de sesgo calculadas para ello; ya podemos hacerlo desde la lección sobre Mapeo normal. Asignamos varios planos a los planos de textura: difusos , normales y desplazamientos , cada uno de los cuales está disponible en el enlace apropiado. En la lección, también utilizaremos el mapeo normal, ya que el mapeo de paralaje crea la ilusión de una topografía de superficie, que se rompe fácilmente si la iluminación no cambia de acuerdo con la topografía. Dado que los mapas normales a menudo se crean sobre la base de mapas de elevación, su uso combinado garantiza la conexión correcta de la iluminación, teniendo en cuenta el terreno.

Probablemente ya haya notado que el mapa de desplazamiento que se muestra en el enlace de arriba es, de hecho, el inverso del mapa que se muestra al comienzo de la lección. La implementación del mapeo Parallax generalmente se lleva a cabo utilizando solo esos mapas, que son inversos a los mapas de altura - mapas de profundidad . Esto sucede porque la imitación de los recesos en el plano es algo más fácil que la imitación de la elevación. De acuerdo con este cambio, el esquema de trabajo de Mapeo de Parallax también cambia:


De nuevo vemos puntos familiares $$$\ color {verde} A$ y $$$\ color {azul} B$ sin embargo, esta vez el vector $$$\ color {marrón} {\ bar {P}}$ obtenido restando el vector $$$\ color {orange} {\ bar {V}}$ de coordenadas de textura en un punto $$$\ color {verde} A$ . Las profundidades en lugar de las alturas se pueden obtener simplemente restando la muestra de profundidad de la unidad o invirtiendo los colores de textura en cualquier editor de imágenes.

El mapeo de paralaje se implementa en el sombreador de fragmentos, ya que los datos de elevación son diferentes para cada fragmento dentro del triángulo. El código del sombreador de fragmentos requerirá el cálculo del vector desde el fragmento hasta el observador $$$\ color {orange} {\ bar {V}}$ , por lo que debe transmitirle la posición del fragmento y el observador en el espacio tangente. De acuerdo con los resultados de la lección sobre el mapeo normal, todavía tenemos el sombreador de vértices en nuestras manos, que transfiere todos estos vectores ya reducidos al espacio tangente, lo usaremos:

#version 330 core layout (location = 0) in vec3 aPos; layout (location = 1) in vec3 aNormal; layout (location = 2) in vec2 aTexCoords; layout (location = 3) in vec3 aTangent; layout (location = 4) in vec3 aBitangent; out VS_OUT { vec3 FragPos; vec2 TexCoords; vec3 TangentLightPos; vec3 TangentViewPos; vec3 TangentFragPos; } vs_out; uniform mat4 projection; uniform mat4 view; uniform mat4 model; uniform vec3 lightPos; uniform vec3 viewPos; void main() { gl_Position = projection * view * model * vec4(aPos, 1.0); vs_out.FragPos = vec3(model * vec4(aPos, 1.0)); vs_out.TexCoords = aTexCoords; vec3 T = normalize(mat3(model) * aTangent); vec3 B = normalize(mat3(model) * aBitangent); vec3 N = normalize(mat3(model) * aNormal); mat3 TBN = transpose(mat3(T, B, N)); vs_out.TangentLightPos = TBN * lightPos; vs_out.TangentViewPos = TBN * viewPos; vs_out.TangentFragPos = TBN * vs_out.FragPos; } 

De las cosas importantes, solo notaré que específicamente para las necesidades de Mapeo de Parallax, es necesario transferir el positionPoser en el espacio tangente al sombreador de fragmentos aPos .

Dentro del sombreador, implementamos el algoritmo de mapeo Parallax, que se parece a esto:

 #version 330 core out vec4 FragColor; in VS_OUT { vec3 FragPos; vec2 TexCoords; vec3 TangentLightPos; vec3 TangentViewPos; vec3 TangentFragPos; } fs_in; uniform sampler2D diffuseMap; uniform sampler2D normalMap; uniform sampler2D depthMap; uniform float height_scale; vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir); void main() { vec3 viewDir = normalize(fs_in.TangentViewPos - fs_in.TangentFragPos); //       Parallax Mapping vec2 texCoords = ParallaxMapping(fs_in.TexCoords, viewDir); //      //     vec3 diffuse = texture(diffuseMap, texCoords); vec3 normal = texture(normalMap, texCoords); normal = normalize(normal * 2.0 - 1.0); //  –     [...] } 

Anunciamos la función ParallaxMapping, que toma las coordenadas de textura del fragmento y el vector del fragmento al observador. $$$\ color {orange} {\ bar {V}}$ en el espacio tangente El resultado de la función son coordenadas de textura desplazadas, que ya se utilizan para muestras de una textura difusa y un mapa normal. Como resultado, el color difuso del píxel y su normalidad corresponden correctamente a la "geometría" cambiada del plano.

¿Qué se esconde dentro de la función ParallaxMapping?

  vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir) { float height = texture(depthMap, texCoords).r; vec2 p = viewDir.xy / viewDir.z * (height * height_scale); return texCoords - p; } 

Esta función relativamente simple es una implementación literal del método, cuyos puntos principales discutimos anteriormente. Se toman las coordenadas de textura iniciales de TexCoords, con la ayuda de las cuales se selecciona la altura (o profundidad) $$$\ color {verde} {H (A)}$ from depthMap para el fragmento actual. Para calcular el vector $$$\ color {marrón} {\ bar {P}}$ el vector viewDir se toma en espacio tangente y el par de sus componentes x e y se divide por el componente z , y el resultado se escala por el valor de desplazamiento de lectura de la altura . El uniforme height_scale también se ha introducido para proporcionar un control adicional sobre la gravedad del efecto de Mapeo de paralaje, ya que el efecto de desplazamiento suele ser demasiado fuerte. Para obtener el resultado, restamos el vector resultante $$$\ color {marrón} {\ bar {P}}$ de las coordenadas de textura originales.

Nos ocuparemos del momento de dividir viewDir.xy en viewDir.z . Como el vector viewDir está normalizado, su componente z se encuentra en el intervalo [0, 1]. Cuando el vector es casi paralelo a la superficie del componente z está cerca de cero, y la operación de división devuelve el vector $$$\ color {marrón} {\ bar {P}}$ mucho más tiempo que si viewDir está cerca de la perpendicular a la superficie. En otras palabras, escalamos el vector $$$\ color {marrón} {\ bar {P}}$ para que aumente cuando mira la superficie en ángulo, esto le permite obtener un resultado más realista en tales casos.

Algunos desarrolladores prefieren eliminar la escala dividiendo por viewDir.z , porque, en ciertos casos, este enfoque da resultados incorrectos cuando se ve desde un ángulo. Esta modificación de la técnica se llama Mapeo de paralaje con limitación de compensación . La elección de una opción de enfoque, en su mayor parte, sigue siendo una cuestión de preferencia personal; por ejemplo, soy más leal a los resultados del algoritmo de mapeo Parallax habitual.

Las coordenadas de textura alteradas resultantes se utilizan en última instancia para seleccionar del mapa difuso y el mapa normal, lo que nos da un efecto de distorsión de superficie bastante bueno (el parámetro height_scale aquí se elige cerca de 0.1):


En la imagen, puede comparar los efectos de las técnicas de Mapeo normal y Mapeo de paralaje. Dado que el Mapeo de Parallax simula las irregularidades de la superficie, esta técnica permite situaciones en las que los ladrillos se superponen, dependiendo de la dirección del ojo.

Extraños artefactos también son visibles a lo largo de los bordes del plano texturizado. Aparecen debido al hecho de que las coordenadas de textura desplazadas por el algoritmo de Mapeo de Parallax pueden quedar fuera del intervalo de la unidad y, dependiendo del modo de ajuste , pueden causar resultados no deseados. Una forma simple de deshacerse de tales artefactos es simplemente descartar todos los fragmentos para los que las coordenadas de textura están fuera del intervalo de la unidad:

 texCoords = ParallaxMapping(fs_in.TexCoords, viewDir); if(texCoords.x > 1.0 || texCoords.y > 1.0 || texCoords.x < 0.0 || texCoords.y < 0.0) discard; 

Como resultado, todos los fragmentos con coordenadas de textura desplazadas que caen fuera del intervalo [0, 1] se descartarán y visualmente el resultado de la acción de Mapeo de paralaje será aceptable. Obviamente, este método de rechazo no es universal y puede no ser aplicable a algunas superficies o casos de texturas. Pero en el ejemplo de un avión, funciona perfectamente y ayuda a fortalecer el efecto de cambiar el relieve del avión:


Las fuentes de muestra están aquí .

Se ve bien, y el rendimiento del método es excelente: ¡todo lo que tomó fue una muestra adicional de la textura! Pero la simplicidad del método tiene inconvenientes significativos: el efecto de alivio se destruye fácilmente cuando se mira el plano en ángulo (lo que también es cierto para el mapeo normal) o si hay secciones en el mapa de altura con cambios bruscos en los valores:


La razón de la destrucción de la ilusión radica en el hecho de que el algoritmo es una aproximación muy aproximada del mapeo de desplazamiento real. Sin embargo, varios trucos adicionales pueden ayudarnos, lo que nos permite obtener resultados casi perfectos incluso al mirar un ángulo o al usar mapas de altura con cambios bruscos. Por ejemplo, podemos usar varias muestras de un mapa de altura para encontrar el punto más cercano al punto $$$\ color {azul} B$ .

Mapeo de paralaje empinado

La técnica Steep Parallax Mapping es un desarrollo lógico del clásico Parallax Mapping: se utiliza el mismo enfoque en el algoritmo, pero en lugar de una sola selección, se toman varios, para una mejor aproximación del vector $$$\ color {marrón} {\ bar {P}}$ usado para calcular el punto $$$\ color {azul} B$ . Debido a estas muestras adicionales, el resultado del algoritmo es visualmente mucho más plausible, incluso cuando se observan ángulos agudos en la superficie.

La base del enfoque Steep PM es tomar un cierto rango de profundidades y dividirlo en capas de igual tamaño. A continuación, iteramos a través de las capas mientras cambiamos simultáneamente las coordenadas de textura originales en la dirección del vector $$$\ color {marrón} {\ bar {P}}$ y hacer muestras del mapa de profundidad, deteniéndose en el momento en que la profundidad de la muestra es menor que la profundidad de la capa actual. Mira el diagrama:


Como puede ver, nos movemos a través de las capas de arriba a abajo y para cada capa comparamos su profundidad con el valor del mapa de profundidad. Si la profundidad de la capa es menor que el valor del mapa de profundidad, esto significa que el vector $$$\ color {marrón} {\ bar {P}}$ correspondiente a esta capa se encuentra por encima de la superficie. Este proceso se repite hasta que la profundidad de la capa es mayor que la selección del mapa de profundidad: en este momento, el vector $$$\ color {marrón} {\ bar {P}}$ apunta a un punto debajo de la topografía de superficie simulada.
El ejemplo muestra que la selección del mapa de profundidad en la segunda capa ( $$$D (2) = 0.73$ ) aún se encuentra "más profundo" con respecto a la profundidad de la segunda capa igual a 0.4, lo que significa que el proceso de búsqueda continúa. En la próxima pasada, una profundidad de capa de 0.6 finalmente resulta estar "por encima" del valor de la muestra del mapa de profundidad ( $$$D (3) = 0.37$ ) De aquí concluimos que el vector $$$\ color {marrón} {\ bar {P}}$ obtenido para la tercera capa es la posición más confiable para la geometría de superficie distorsionada. Puedes usar coordenadas de textura $$$T_3$ derivado del vector $$$\ color {marrón} {\ bar {P}}$ , para compensar las coordenadas de textura del fragmento actual. Obviamente, la precisión del método crece con el número de capas.

Los cambios en la implementación afectarán solo a la función ParallaxMapping, ya que ya contiene todas las variables necesarias para que el algoritmo funcione:

 vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir) { //    const float numLayers = 10; //    float layerDepth = 1.0 / numLayers; //    float currentLayerDepth = 0.0; //         //     P vec2 P = viewDir.xy * height_scale; vec2 deltaTexCoords = P / numLayers; [...] } 

Primero, inicializamos: establecemos el número de capas, calculamos la profundidad de cada una de ellas y, finalmente, encontramos el tamaño del desplazamiento de las coordenadas de textura a lo largo de la dirección del vector $$$\ color {marrón} {\ bar {P}}$ , que deberá desplazarse en cada capa.

El siguiente es un pasaje a través de las capas, comenzando desde la parte superior, hasta que se encuentra una selección del mapa de profundidad que se encuentra "por encima" del valor de profundidad de la capa actual:

 //   vec2 currentTexCoords = texCoords; float currentDepthMapValue = texture(depthMap, currentTexCoords).r; while(currentLayerDepth < currentDepthMapValue) { //      P currentTexCoords -= deltaTexCoords; //          currentDepthMapValue = texture(depthMap, currentTexCoords).r; //     currentLayerDepth += layerDepth; } return currentTexCoords; 

En este código, atravesamos todas las capas de profundidad y cambiamos las coordenadas de textura originales hasta que la selección del mapa de profundidad sea menor que la profundidad de la capa actual. El desplazamiento se lleva a cabo restando de las coordenadas de textura originales del delta en función del vector $$$\ color {marrón} {\ bar {P}}$ . El resultado del algoritmo es un vector de desplazamiento de coordenadas de textura, definido con mucha mayor precisión que el mapeo de Parallax clásico.

Usando aproximadamente 10 muestras, el ejemplo de ladrillo se vuelve mucho más realista, incluso cuando se ve desde un ángulo. Pero lo mejor de todo, las ventajas de Steep PM son visibles en superficies con un mapa de profundidad, que tiene cambios bruscos en los valores. Por ejemplo, como en este juguete de madera, ya demostrado anteriormente:


Puede mejorar el algoritmo un poco más si analiza un poco las características de la técnica de Mapeo de Parallax. Si miras la superficie aproximadamente normal, entonces no hay necesidad de cambiar fuertemente las coordenadas de textura, mientras que cuando miras un ángulo, el cambio tiende al máximo (imagina mentalmente la dirección de la vista en ambos casos). Si parametriza el número de muestras dependiendo de la dirección de su mirada, puede ahorrar bastante cuando no se necesitan muestras adicionales:

 const float minLayers = 8.0; const float maxLayers = 32.0; float numLayers = mix(maxLayers, minLayers, abs(dot(vec3(0.0, 0.0, 1.0), viewDir))); 

El resultado del producto escalar del vector viewDir y el semieje positivo Z se usa para determinar el número de capas en el intervalo [ minSamples , maxSamples ], es decir la dirección de la mirada determina el número requerido de iteraciones del efecto (en el espacio tangente, el semieje positivo Z se dirige normal a la superficie). Si miramos en paralelo a la superficie, el efecto usaría las 32 capas.

El código fuente modificado está aquí . También propongo descargar la textura de un juguete de madera: mapa difuso , normal , mapa de profundidad .

No sin un enfoque y desventajas. Dado que el número de muestras es todo el mismo finito, la aparición de efectos de aliasing es inevitable, lo que hace que las transiciones entre capas sean sorprendentes:


Puede reducir la gravedad del artefacto al aumentar el número de muestras utilizadas, pero rápidamente consume todo el rendimiento del procesador de video disponible. Hay varias adiciones al método, que devuelven como resultado no el primer punto que apareció bajo el relieve imaginario de la superficie, sino el valor interpolado de las dos capas más cercanas, lo que nos permite aclarar aún más la posición del punto. $$$\ color {azul} B$ .

De estos métodos, dos se usan con mayor frecuencia: Relief Parallax Mapping y Parallax Occlusion Mapping , con Relief PM dando los resultados más confiables, pero también es un poco más exigente en cuanto al rendimiento en comparación con Parallax Occlusion Mapping. Dado que Parallax Occlusion Mapping sigue siendo bastante similar en calidad a Relief PM y al mismo tiempo funciona más rápido, prefieren usarlo con mayor frecuencia. A continuación, se considerará la implementación del mapeo de oclusión Parallax.

Mapeo de oclusión de paralaje

El método de mapeo de oclusión de Parallax funciona con los mismos principios básicos que Steep PM, pero en lugar de usar las coordenadas de textura de la primera capa, donde se encontró una intersección con un relieve imaginario, el método usa interpolación lineal entre dos capas: la capa después y antes de la intersección. El coeficiente de ponderación para la interpolación lineal se basa en la relación entre la profundidad de relieve actual y las profundidades de ambas capas en consideración. Eche un vistazo al diagrama para comprender mejor cómo funciona todo:


Como puede ver, todo es muy similar a Steep PM, solo se agrega un paso adicional de interpolar las coordenadas de textura de las dos capas de profundidad adyacentes al punto de intersección. Por supuesto, este método es solo una aproximación, pero mucho más preciso que Steep PM.

El código de mapeo de oclusión de Parallax se suma al código Steep PM y no es demasiado complicado:

 [...] // ,    Steep PM //       , // ..  " " vec2 prevTexCoords = currentTexCoords + deltaTexCoords; //         //      float afterDepth = currentDepthMapValue - currentLayerDepth; float beforeDepth = texture(depthMap, prevTexCoords).r - currentLayerDepth + layerDepth; //    float weight = afterDepth / (afterDepth - beforeDepth); vec2 finalTexCoords = prevTexCoords * weight + currentTexCoords * (1.0 - weight); return finalTexCoords; 

En el momento de encontrar la capa situada después del punto de intersección con el relieve imaginario, también determinamos las coordenadas de textura de la capa situada antes del punto de intersección. A continuación, encontramos los desplazamientos de la profundidad de relieve imaginaria en relación con las profundidades de las dos capas consideradas y utilizamos su relación como el coeficiente de peso de una mayor interpolación lineal de las coordenadas de textura correspondientes a las dos capas consideradas. El resultado de la interpolación es devuelto por la función para uso futuro.

El mapeo de oclusión de Parallax ofrece resultados sorprendentemente visualmente confiables, aunque con pequeños defectos y artefactos de alias. Pero para comprometer la velocidad y la calidad, son insignificantes y solo aparecen con una observación cercana de la superficie cerca de la cámara o con ángulos de visión muy nítidos.


Un código de ejemplo está aquí .

Parallax Mapping es realmente una excelente técnica que le permite aumentar drásticamente los detalles visuales de su escena, pero, por supuesto, tiene sus inconvenientes en forma de artefactos, que vale la pena recordar al implementar la técnica en el proyecto. En su mayor parte, el mapeo de paralaje se usa en superficies planas como paredes o pisos, donde no es tan fácil determinar el contorno de todo el objeto y el ángulo de visión de la superficie a menudo está cerca de la perpendicular. En este caso, los defectos de Mapeo de Parallax son casi invisibles, en el contexto de un mayor detalle de la superficie.

Bonificaciones del traductor:

Mapeo de paralaje en relieve

Como el autor mencionó dos métodos para aclarar el resultado de Steep PM, para completar, describiré el segundo de los enfoques.

Al igual que Parallax Occlusion Mapping, el resultado de la ejecución de Steep PM se usa aquí, es decir. sabemos las profundidades de dos capas entre las cuales se encuentra el punto real de intersección del vector $$$\ color {orange} {\ bar {V}}$ con relieve, así como las correspondientes coordenadas de textura $$$T_2$ y $$$T_3$ . El refinamiento de la estimación del punto de intersección en este método se debe al uso de la búsqueda binaria.

Algoritmo de refinamiento pasos:

• Realice el cálculo Steep PM y obtenga coordenadas de textura $$$T_2$ y $$$T_3$ - en este intervalo se encuentra el punto de intersección del vector $$$\ color {green} {\ bar {V}}$ con topografía de superficie. La verdadera intersección está marcada con una cruz roja.
• Divida en dos valores actuales para el desplazamiento de las coordenadas de textura y la altura de la capa de profundidad.
• Mover coordenadas de textura desde el punto $$$T_3$ en la dirección opuesta al vector $$$\ color {green} {\ bar {V}}$ por la cantidad de desplazamiento. Reduzca la profundidad de la capa por el valor de tamaño de capa actual.
• Búsqueda directa binaria. Se repite el número especificado de iteraciones:
• 1. Seleccione del mapa de profundidad. Divida el desplazamiento de textura actual y el tamaño de la capa de profundidad en dos valores actuales.
  2. Si el tamaño de la muestra es mayor que la profundidad de la capa actual, aumente la profundidad de la capa por el tamaño de la capa actual y cambie las coordenadas de textura a lo largo del vector $$$\ color {green} {\ bar {V}}$ al desplazamiento actual.
  3. Si el tamaño de la muestra es menor que la profundidad de la capa actual, reduzca la profundidad de la capa por el tamaño de la capa actual y cambie las coordenadas de textura a lo largo del vector inverso $$$\ color {green} {\ bar {V}}$ al desplazamiento actual.
  
  
• Las últimas coordenadas de textura obtenidas son los resultados de Relief PM.

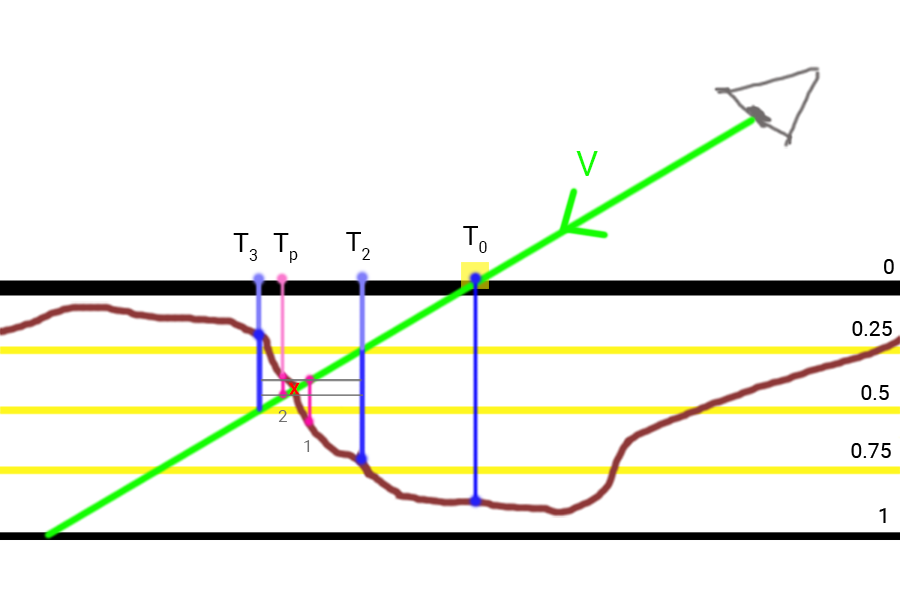
La imagen muestra que después de encontrar los puntos $$$T_2$ y $$$T_3$ reducimos a la mitad el tamaño de la capa y el tamaño del desplazamiento de las coordenadas de textura, lo que nos da el primer punto de iteración de la búsqueda binaria (1). Dado que el tamaño de la muestra resultó ser mayor que la profundidad actual de la capa, reducimos a la mitad los parámetros nuevamente y avanzamos $$$\ color {green} {\ bar {V}}$ obteniendo punto (2) con coordenadas de textura $$$T_p$ que será el resultado de Steep PM para dos iteraciones de la búsqueda binaria.

Código de sombreador:

 //  : inTexCoords -   , // inViewDir -      - //  : lastDepthValue –      //      vec2 reliefPM(vec2 inTexCoords, vec3 inViewDir, out float lastDepthValue) { // ====== // ,   Steep PM // ====== const float _minLayers = 2.; const float _maxLayers = 32.; float _numLayers = mix(_maxLayers, _minLayers, abs(dot(vec3(0., 0., 1.), inViewDir))); float deltaDepth = 1./_numLayers; // uDepthScale –     PM vec2 deltaTexcoord = uDepthScale * inViewDir.xy/(inViewDir.z * _numLayers); vec2 currentTexCoords = inTexCoords; float currentLayerDepth = 0.; float currentDepthValue = depthValue(currentTexCoords); while (currentDepthValue > currentLayerDepth) { currentLayerDepth += deltaDepth; currentTexCoords -= deltaTexcoord; currentDepthValue = depthValue(currentTexCoords); } // ====== //   Relief PM // ====== //         deltaTexcoord *= 0.5; deltaDepth *= 0.5; //      ,   Steep PM currentTexCoords += deltaTexcoord; currentLayerDepth -= deltaDepth; //    … const int _reliefSteps = 5; int currentStep = _reliefSteps; while (currentStep > 0) { currentDepthValue = depthValue(currentTexCoords); deltaTexcoord *= 0.5; deltaDepth *= 0.5; //       , //       if (currentDepthValue > currentLayerDepth) { currentTexCoords -= deltaTexcoord; currentLayerDepth += deltaDepth; } //       else { currentTexCoords += deltaTexcoord; currentLayerDepth -= deltaDepth; } currentStep--; } lastDepthValue = currentDepthValue; return currentTexCoords; } 

Auto-sombreado

También una pequeña adición sobre agregar sombreado de una fuente de luz seleccionada al algoritmo de cálculo. Decidí agregar, porque técnicamente el método de cálculo es idéntico a los considerados anteriormente, pero el efecto sigue siendo interesante y agrega detalles.

De hecho, se aplica el mismo Steep PM, pero la búsqueda no se profundiza en la superficie simulada a lo largo de la línea de visión, sino desde la superficie, a lo largo del vector hasta la fuente de luz$$$\color{green}{\bar{L}}$ .Este vector también se transfiere al espacio tangente y se usa para determinar la cantidad de desplazamiento de las coordenadas de textura. A la salida del método, se obtiene un coeficiente de iluminación del material en el intervalo [0, 1], que se utiliza para modular los componentes difusos y espejos en los cálculos de iluminación.
Para definir el sombreado con bordes afilados, simplemente camine a lo largo del vector$$ˉ L hasta que un punto se encuentre debajo de la superficie. Tan pronto como se encuentre dicho punto, tomamos el coeficiente de iluminación 0. Si alcanzamos la profundidad cero sin encontrar un punto debajo de la superficie, entonces tomamos el coeficiente de iluminación igual a 1.Para determinar el sombreado con bordes suaves, es necesario verificar varios puntos que se encuentran en el vector$\color{green}{\bar{L}}$

$$ˉ L y ubicado debajo de la superficie. El factor de sombreado se toma igual a la diferencia entre la profundidad de la capa actual y la profundidad del mapa de profundidad. También se tiene en cuenta la eliminación del siguiente punto del fragmento en cuestión en forma de un coeficiente de peso igual a (1.0 - stepIndex / numberOfSteps). En cada paso, un coeficiente parcial de iluminación se determina como:$\color{green}{\bar{L}}$

$$

$$PSF_i=(layerHeight_i - heightFromtexture_i)*(1.0-\frac{i}{numSteps})$$

El resultado final es el factor de luz máximo de todo parcial:

$$

$$SF=max(PSF_i)$$

El esquema del método:

El progreso del método para tres iteraciones en este ejemplo:

• Inicializamos el factor de luz total a cero.
• Da un paso a lo largo del vector $$ˉ L , llegando al punto$\color{green}{\bar{L}}$$$$H_a$ . La profundidad del punto es claramente menor que la selección del mapa. $$H ( T L 1 ) : está debajo de la superficie. Aquí realizamos el primer control y, recordando el número total de controles, encontramos y guardamos el primer factor de luz parcial: (1.0 - 1.0 / 3.0).$H(T_{L1})$
• Da un paso a lo largo del vector $$ˉ L , llegando al punto$\color{green}{\bar{L}}$$$$H_b$ . La profundidad del punto es claramente menor que la selección del mapa. $$H ( T L 2 ) : está debajo de la superficie. La segunda verificación y el segundo coeficiente parcial: (1.0 - 2.0 / 3.0).$H(T_{L2})$
• Damos un paso más a lo largo del vector y llegamos a la profundidad mínima de 0. Detenga el movimiento.
• Definición del resultado: si no se encontraron puntos debajo de la superficie, entonces devolvemos un coeficiente igual a 1 (sin sombreado). De lo contrario, el coeficiente resultante se convierte en el máximo de los parciales calculados. Para usar en los cálculos de iluminación, restamos este valor de la unidad.

Ejemplo de código de sombreador:

 //  : inTexCoords -   , // inLightDir -       - //  : inLastDepth –    , //      PM //       //    float getParallaxSelfShadow(vec2 inTexCoords, vec3 inLightDir, float inLastDepth) { float shadowMultiplier = 0.; //      , //    float alignFactor = dot(vec3(0., 0., 1.), inLightDir); if (alignFactor > 0.) { //   :  ,  //  ,     const float _minLayers = 16.; const float _maxLayers = 32.; float _numLayers = mix(_maxLayers, _minLayers, abs(alignFactor)); float _dDepth = inLastDepth/_numLayers; vec2 _dtex = uDepthScale * inLightDir.xy/(inLightDir.z * _numLayers); //  ,    int numSamplesUnderSurface = 0; //       //     L float currentLayerDepth = inLastDepth - _dDepth; vec2 currentTexCoords = inTexCoords + _dtex; float currentDepthValue = depthValue(currentTexCoords); //    float stepIndex = 1.; // ,       … while (currentLayerDepth > 0.) { //     ,     //       if (currentDepthValue < currentLayerDepth) { numSamplesUnderSurface++; float currentShadowMultiplier = (currentLayerDepth - currentDepthValue)*(1. - stepIndex/_numLayers); shadowMultiplier = max(shadowMultiplier, currentShadowMultiplier); } stepIndex++; currentLayerDepth -= _dDepth; currentTexCoords += _dtex; currentDepthValue = depthValue(currentTexCoords); } //      ,   //      1 if (numSamplesUnderSurface < 1) shadowMultiplier = 1.; else shadowMultiplier = 1. - shadowMultiplier; } return shadowMultiplier; } 

El coeficiente resultante se utiliza para modular el resultado del modelo de iluminación Blinn-Fong utilizado en los ejemplos:

 [...] //      vec3 fullColorADS = ambientTerm + attenuation * (diffuseTerm + specularTerm); //     -  fullColorADS *= pmShadowMultiplier; return fullColorADS; 

Comparación de todos los métodos en un collage, volumen de 3 MB.

También una comparación de video:

Materiales adicionales

• Mapeo de oclusión de paralaje en GLSL : una gran lección de mapeo de paralaje de sunandblackcat.com .
• Cómo funciona el mapeo de desplazamiento de Parallax : un video tutorial que explica los detalles del mapeo de Parallax de TheBennyBox .

PD : Tenemos un telegrama conf para la coordinación de transferencias. Si tiene un serio deseo de ayudar con la traducción, ¡de nada!