👩🏽‍🤝‍👨🏼 🕖 🏩 Fórmula Tupper e implementación del algoritmo en Python 🎖️ 💪🏻 👉🏼

En lugar del prólogo

No hace mucho tiempo, en Internet, aprendí sobre una copia tan maravillosa y sorprendente de la biblioteca de Babilonia como la fórmula Tapper . Más bien, es más la desigualdad de Tupper que la fórmula. La peculiaridad de esta desigualdad es que crea su propia imagen en el gráfico. ¡Solo mira este milagro!

imagen

(Fuente de Wikipedia)

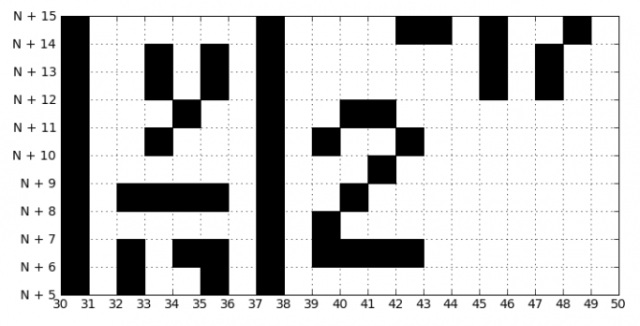
Lo que ves en la imagen es la fórmula de ese mismo Jeff Tupper. Probablemente, la mitad de los lectores ya han ido al tungsteno para dibujar el resultado de esta desigualdad ... Pero esto no es tan simple. Como puede ver en esta imagen, la fórmula en el gráfico se puede ver en un segmento a lo largo del eje OY [k; k + 15]. ¿Cuál es este misterioso número k? ¿Dónde conseguirlo? ¡La cuestión es que esta desigualdad, según el concepto de la biblioteca de Babilonia, puede mostrar absolutamente cualquier imagen con una resolución de 106x17! Cada imagen tiene su propia posición en el gráfico, por lo tanto tiene un número único k. ¡Por lo tanto, para cada número k hay una sola imagen en todo el gráfico !

Para una imagen dada, el número k es el siguiente:

4858450636189713423582095962494202044581400587983244549483093085061934704708809928450644769865524364849997247024915119110411605739177407856919754326571855442057210445735883681829823754139634338225199452191651284348332905131193199953502413758765239264874613394906870130562295813219481113685339535565290850023875092856892694555974281546386510730049106723058933586052544096664351265349363643957125565695936815184334857605266940161251266951421550539554519153785457525756590740540157929001765967965480064427829131488548259914721248506352686630476300

Es interesante observar a las personas que se desplazarán a dicha coordenada para ver la fórmula.

Se me ocurrió escribir un programa en Python3 que convertiría una imagen en un número k y viceversa y le informaría sobre otra excelente forma de codificar una imagen en un número.

Teoría

(Agregado) ¿Cómo funciona?

Echemos un vistazo a la fórmula en sí:
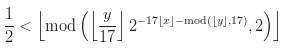
imagen

Definamos su sintaxis:
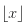
imagen

- número redondeado hacia abajo
mod (x, y) - resto de dividir x por y

Y luego, al parecer, todo está claro.
Tenga en cuenta que tanto x como y se redondean hacia abajo. Es este redondeo lo que finalmente nos da una imagen de píxeles
imagen

Denote todo lo que se redondea en el lado derecho de la desigualdad por

a l p h a

$\ alpha$ .
Entonces

1 / 2 < [a l p h a] <=> 1 <= [a l p h a]

$1/2 <[\ alpha] <=> 1 <= [\ alpha]$

Lo cual es obvio, porque toda la expresión se redondea hacia abajo.

Sea y = 17r + q, donde r es la parte entera de dividir y por 17, y r es el resto de la división. Por lo tanto, podemos reemplazar en la fórmula

[a / 17]

$[a / 17]$ en r, y

m o d (y, 17)

$mod (y, 17)$ en q.

Nosotros obtenemos

1 <= m o d (q * 2^{- 17 - r}, 2)

$1 <= mod (q * 2 ^ {- 17-r}, 2)$

O de lo contrario

1 <= m o d (q / 2^{17 x + r}, 2)

$1 <= mod (q / 2 ^ {17x + r}, 2)$

mod (

a l p h a

$\ alpha$ , 2) toma 2 valores - 0 o 1. En consecuencia, esta desigualdad dirá si el número

q / 2^{17 x + r}

$q / 2 ^ {17x + r}$ incluso o no

Tenga en cuenta que la imagen se ve en el intervalo [N, N + 16], respectivamente

q = [y / 17]

$q = [y / 17]$ permanece constante en toda la altura de la imagen, lo que no se puede decir sobre el número r (en toda la imagen varía de 0 a 16).

Y ahora la guinda del pastel. Numero

[q / 2^{17 x + r}]

$[q / {2 ^ {17x + r}}]$ será impar si y solo si el número de bit (17x + r) en la representación binaria de q es igual a 1. Y dado que el número q cambia constantemente con su altura y su representación binaria también, ¡siempre obtenemos una imagen única! Eso es exactamente lo que funciona la fórmula de Tapper.

Ahora veamos cómo calcular la altura a la que queremos ver nuestra imagen

El principio de calcular el número k

El mismo Tupper describió el cálculo del número k para cualquier imagen de 106x17 (¡esto es importante!) De la siguiente manera:

Convertir imagen a blanco y negro
Lea cada píxel de abajo hacia arriba, de izquierda a derecha y colóquelo en el búfer. Si el píxel es negro, ponga 1, si es blanco, 0.
Convertir binario a decimal y multiplicar por 17
Beneficio!

Para obtener una imagen del número k, hacemos todo exactamente lo contrario. Bueno, vamos a codificar!

Kodim

UPD: En los comentarios, la gente mejoró un poco el código, lo hizo más simple y más transparente. Este artículo ha publicado datos de actualización. Si desea ver las versiones anteriores del código, vaya al repositorio de github (hasta que lo confirme, enlace al final del artículo) y en el comentario

De k a imagen

UPD

A pedido de los comentaristas, se agregó una nueva forma de calcular la imagen utilizando esta desigualdad y k! ¡Ahora no haremos manipulaciones con el número, transferiremos al sistema binario, sino que afectaremos directamente la función en sí!

Usando el método Tapper para decodificar el número k

Obtenemos el número k del usuario, ~~con los ojos cerrados lo~~ dividimos por 17 y lo traducimos al sistema binario.

 def from_k_to_bin(k: int) -> list: k //= 17 binary = bin(k)[2:]

Entendemos que algunos píxeles iniciales pueden ser blancos (igual a 0), respectivamente, para nuestro número binario, los primeros bits serán ceros, y al traducir un número a un sistema decimal, estos ceros iniciales se perderán. Por lo tanto, verificamos el tamaño del número binario resultante, si es menor que 1802, luego agregamos ceros al principio.

 def from_k_to_bin(k: int) -> list: k //= 17 binary = bin(k)[2:] #   RadicalDreamer binary = ("0" * (1802 - len(binary))) + binary

A continuación, declare una lista bidimensional en la que almacenaremos información sobre cada línea de la imagen. Luego escribimos todos esos bits que leemos (no olvide el algoritmo por el cual se crea el número k, de abajo hacia arriba, de izquierda a derecha)

 lists = [[] for x in range(17)] #C   RadicalDreamer for x in range(1802): lists[-(x % 17)].append(binary[x]) <b> !</b> <source lang="python"> #-----!-----# image = Image.new("1", (106,17), (0)) # -  10617 draw = image.load() for y in range(17): for x in range(106): image.putpixel(xy=(105-x,16-y), value=(int(lists[y][x]),)) #    ,      lists image.save("image.png") #

Intentemos insertar el número k, que indiqué al principio del artículo, en nuestro programa y obtener lo siguiente:

imagen

Como puede ver, todo funcionó para nosotros, ¡y ahora podemos decodificar cualquier k!

Usando la desigualdad para generar una imagen de k

Primero, escribe la función en python:

 def f(x,y): return ((y//17)//(1 << (17*x+(y%17))))%2

Gracias a los operadores // y <<, la implementación de la función se ha simplificado enormemente. ¡Se garantiza que los números x e y serán enteros !

Nuevamente creamos una lista bidimensional, donde almacenaremos los bits de la imagen y escribiremos información sobre cada línea usando bucles.

 lists = [[] for x in range(17)] for y in range(16,-1,-1): for x in range(105,-1,-1): lists[y].append(int(f(x,y+k) > 1/2))

Y luego, como en el ejemplo anterior, dibujamos una imagen usando la biblioteca PIL.

La función completa se ve así:

 def from_k_to_bin(k: int) -> list: lists = [[] for x in range(17)] for y in range(16,-1,-1): for x in range(105,-1,-1): lists[y].append(int(f(x,y+k) > 1/2)) return lists

Imagen en k

Bueno, ahora aprenderemos a codificar cualquier imagen en el número k.

Primero obtenemos la imagen en sí

 def get_image() -> Image: name = input("   (      ):") try: im = Image.open(name) except Exception: print("!") exit(0) return im

Comprueba su tamaño

 _SIZE_WIDTH = 106 _SIZE_HEIGHT = 17 image = get_image() width, height = image.size flag_okay = False if width == _SIZE_WIDTH and height == _SIZE_HEIGHT: flag_okay = True if not flag_okay: print("  ") print(width, height) exit(0) print(" !")

Hacemos la imagen en blanco y negro y comenzamos a leer píxel por píxel:

 image = image.convert('1') byteset = "" for x in range(105,-1,-1): for y in range(0,17): #c m03r   if image.getpixel((x,y)) > 127: byteset += '1' else: byteset += '0'

Solo resta convertir al sistema decimal y multiplicar por 17.

 k = int(byteset,2)*17 print(" :") print(k)

Bueno, vamos a probar!

Decidí codificar el logotipo de habr. Aquí está la imagen de origen:

imagen

Iniciamos el programa y especificamos el nombre de la imagen:

imagen

Tenemos la siguiente k:

4858487703217654168507377107565676789145697178497253677539145555247620343537955749299116772611982962556356527603203744742682135448820545638134012705381689785851604674225344958377377969928942310236199337805399065932982909660659786056259547094494380793146587709009524498386724160055692719747815828234655968636671461350354316223620304956111171025410498514602810746287134775641383930152393933036921599511277388743068766568352667661462097979110006690900253037600818522726237351439443865433159187625289316917268254866954663750093103703327097252478959

Vamos a verlo en nuestro propio programa.

Aquí está la imagen que recibimos:

imagen

Estaba un poco distorsionado debido a una traducción ligeramente torcida de la imagen en blanco y negro.

Resumen

Código fuente: Github

Fuentes: artículo de Wiki

Fórmula Tupper e implementación del algoritmo en Python