Saludos a todos, y especialmente a aquellos interesados en matemáticas discretas y teoría de grafos.
Antecedentes
Dio la casualidad de que, impulsado por el interés, estaba desarrollando un servicio de construcción de tours. rutas. La tarea consistía en planificar las mejores rutas en función de la ciudad de interés para el usuario, las categorías de establecimientos y el marco temporal. Bueno, una de las subtareas fue calcular el tiempo de viaje de una institución a otra. Como era joven y estúpido, resolví este problema de frente, con el algoritmo de Dijkstra, pero para ser justos, vale la pena señalar que solo con eso era posible iniciar la iteración de un nodo a miles de otros, almacenar estas distancias no era una opción, las instituciones de más de 10k solo en Moscú solo, y decisiones como la distancia de Manhattan en nuestras ciudades no funcionan en absoluto.
Y resultó que era posible resolver el problema de rendimiento en el problema combinatorio, pero la mayor parte del tiempo para procesar la solicitud se dedicó a la búsqueda de rutas no almacenadas en caché. El problema se complicó por el hecho de que el gráfico de carreteras de Osm en Moscú es bastante grande (medio millón de nodos y 1,1 millones de arcos).
No hablaré sobre todos los intentos y, de hecho, el problema podría resolverse cortando los arcos adicionales del gráfico, solo le diré que en algún momento me di cuenta y me di cuenta de que si se acerca al algoritmo de Dijkstra desde el punto de vista del enfoque probabilístico, Puede ser lineal.
Dijkstra para el tiempo logarítmico
Todo el mundo sabe, pero quién sabe, leer que el algoritmo de Dijkstra mediante el uso de una cola con la complejidad logarítmica de insertar y eliminar puede conducir a la complejidad de la forma O (n log (n) + m log (n)). Cuando se usa el montón de Fibonacci, la complejidad se puede reducir a O (n * log (n) + m), pero aún no es lineal, pero me gustaría.
En el caso general, el algoritmo de cola se describe de la siguiente manera:
Dejar:
- V es el conjunto de vértices gráficos
- E es el conjunto de aristas del gráfico
- w [i, j] es el peso del borde del nodo i al nodo j
- a - inicio del vértice de la búsqueda
- cola q-vertex
- d [i] - distancia al nodo i-ésimo
- d [a] = 0, para todos los demás d [i] = + inf
Mientras q no está vacío:
- v es el vértice con el mínimo d [v] de q
- Para todos los vértices u para los cuales hay una transición a E desde el vértice v
- si d [u]> w [vu] + d [v]
- eliminar u de q con la distancia d [u]
- d [u] = w [vu] + d [v]
- agregue u a q con la distancia d [u]
- eliminar v de q
Si usamos un árbol rojo-negro como una cola, donde la inserción y eliminación ocurren en log (n), y la búsqueda del elemento mínimo es similar en log (n), entonces la complejidad del algoritmo es O (n log (n) + m log (n)) .
Y aquí vale la pena señalar una característica importante: nada impide, en teoría, considerar la parte superior varias veces. Si el vértice ha sido examinado y la distancia a él se ha actualizado a un valor incorrecto, mayor que el verdadero, entonces, siempre que tarde o temprano el sistema converja y la distancia a usted se actualice al valor correcto, está permitido hacer tales trucos. Pero vale la pena señalar: un vértice debe considerarse más de 1 vez con poca probabilidad.
Ordenar tabla hash
Para reducir el tiempo de ejecución del algoritmo de Dijkstra a uno lineal, se propone una estructura de datos, que es una tabla hash con números de nodo (node_id) como valores. Observo que la necesidad de la matriz d no desaparece, todavía es necesaria para obtener la distancia al i-ésimo nodo en tiempo constante.
La siguiente figura muestra un ejemplo de la estructura propuesta.
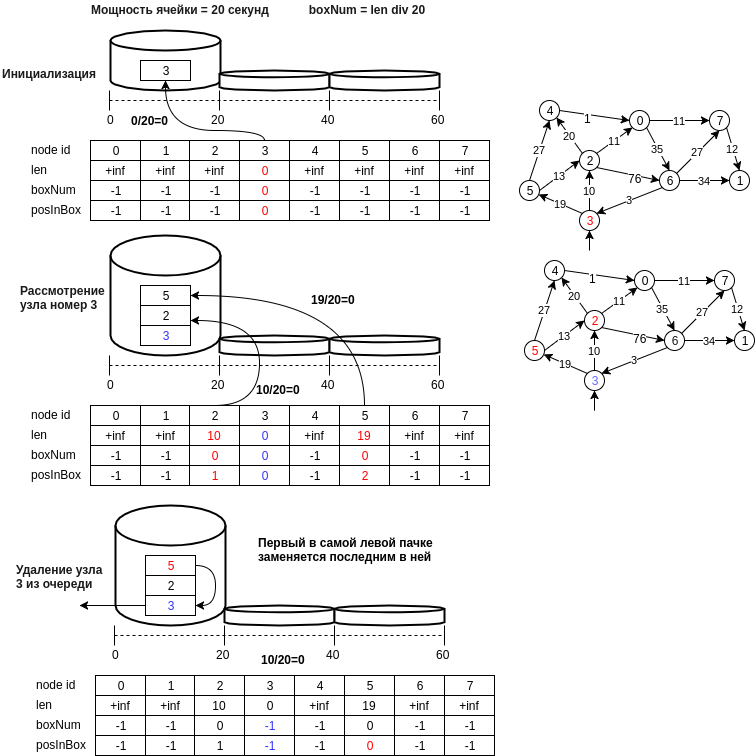
Describamos en pasos la estructura de datos propuesta:
- el nodo u se escribe en la celda con un número igual a d [u] // bucket_size, donde bucket_size es la potencia de la celda (por ejemplo, 20 metros, es decir, la celda en el número 0 contendrá nodos cuya distancia se ubicará en el rango [0, 20) metros )
- el último nodo de la primera celda no vacía, es decir La operación de extracción del elemento mínimo se realizará en O (1). Es necesario mantener el estado actual del identificador del número de la primera celda no vacía (min_el).
- la operación de inserción se realiza agregando un nuevo número de nodo al final de la celda y también ejecutando O (1), porque El cálculo del número de celda ocurre en un tiempo constante.
- la operación de eliminación, como en el caso de una tabla hash, es posible una enumeración normal, y se podría suponer y decir que con un tamaño de celda pequeño esto también es O (1). Si no le importa la memoria (en principio, y no se necesita mucho, otra matriz por n), puede crear una matriz de posiciones en la celda. En este caso, si el elemento se elimina en el medio de la celda, es necesario mover el último valor de la celda a la ubicación eliminada.
- un punto importante al elegir el elemento mínimo: es mínimo solo con cierta probabilidad, pero el algoritmo mirará la celda min_el hasta que se vacíe y tarde o temprano se considerará el elemento mínimo real, y si accidentalmente actualizamos el valor de la distancia al nodo accesible desde mínimo, entonces los nodos adyacentes al mínimo pueden estar nuevamente en la cola y la distancia a ellos será correcta, etc.
- También puede eliminar celdas vacías hasta min_el, ahorrando así memoria. En este caso, la eliminación del nodo v de la cola q debe hacerse solo después de considerar todos los nodos adyacentes.
- y también puede cambiar la potencia de la celda, los parámetros para aumentar el tamaño de la celda y la cantidad de celdas cuando necesita aumentar el tamaño de la tabla hash.
Resultados de medida
Los controles se realizaron en el mapa osm de Moscú, se descargaron a través de osm2po en postgres y luego se cargaron en la memoria. Las pruebas fueron escritas en Java. Había 3 versiones del gráfico:
- gráfico fuente: 0,43 millones de nodos, 1,14 millones de arcos
- versión comprimida del gráfico con 173k nodos y 750k arcos
- versión peatonal de la versión comprimida del gráfico, 450k arcos, 100k nodos.
A continuación se muestra una imagen con medidas en diferentes versiones del gráfico:

Considere la dependencia de la probabilidad de volver a ver el vértice y el tamaño del gráfico:
| cantidad de vistas de nodo | contar vértices | probabilidad de volver a ver el nodo |
|---|
| 104915 | 100015 | 4.8 |
| 169429 | 167892 | 0.9 |
| 431490 | 419594 | 2.8 |
Puede notar que la probabilidad no depende del tamaño del gráfico y es bastante específica para la solicitud, pero es pequeña y su rango se configura cambiando la potencia de la celda. Estaría muy agradecido por la ayuda en la construcción de una modificación probabilística del algoritmo con parámetros que garanticen un intervalo de confianza dentro del rango del cual la probabilidad de visualización repetida no exceda un cierto porcentaje.
También se llevaron a cabo mediciones cualitativas para confirmar prácticamente la comparación de la exactitud del resultado de los algoritmos con la nueva estructura de datos, que mostró una coincidencia completa de la longitud de ruta más corta de 1000 nodos aleatorios a 1000 otros nodos aleatorios en el gráfico. (y así sucesivamente 250 iteraciones) cuando se trabaja con una tabla hash de clasificación y un árbol rojo-negro.
El código fuente de la estructura de datos propuesta se encuentra en el enlace.
PD: Conozco el algoritmo Torup y el hecho de que resuelve el mismo problema en tiempo lineal, pero no pude dominar este trabajo fundamental en una noche, aunque entendí la idea en términos generales. Al menos, según tengo entendido, se propone otro enfoque allí, basado en la construcción de un árbol de expansión mínimo.
PSS Dentro de una semana intentaré encontrar el tiempo y hacer una comparación con el grupo Fibonacci y un poco más tarde agregaré nabo github con ejemplos y códigos de prueba.