Optimización de la colocación de máquinas virtuales en servidores.

Hace algún tiempo, uno de mis colegas dijo que el lugar en el DC se está agotando, que no hay ningún lugar para colocar el servidor, y que la carga está creciendo y no está claro qué hacer, y probablemente tendrá que cambiar todos los servidores disponibles por otros más potentes.

En ese momento estaba involucrado en la tarea de compilar horarios óptimos, y pensé, pero ¿qué pasa si aplicamos algoritmos de optimización para aumentar la utilización del servidor en DC? De aquí nació el proyecto sobre el que quiero escribir.

Para los usuarios avanzados, diré de inmediato que en este artículo hablaremos sobre el embalaje de contenedores, y para el resto que quieran saber cómo ahorrar hasta un 30% de los recursos del servidor utilizando cálculos relativamente simples, bienvenidos a cat.

Entonces, tenemos un DC con aproximadamente 100 servidores, que alojan aproximadamente 7,000 máquinas virtuales. Qué hay dentro de las máquinas virtuales: no lo sabemos y no debemos saberlo. Es necesario colocar máquinas virtuales en los servidores para realizar el SLA y al mismo tiempo usar el número mínimo de servidores.

Nosotros sabemos:

• lista de servidores
• cantidad de recursos en cada servidor (tiempo de CPU, núcleos de CPU, RAM, disco, disco io, red io).
• lista de máquinas virtuales (VM)
• La cantidad de recursos consumidos por cada máquina virtual (tiempo de CPU, núcleos de CPU, RAM, disco, disco io, red io).
• consumo de recursos por el sistema host en los servidores.

Necesitamos distribuir máquinas virtuales entre los servidores para que cada uno de los recursos en cada servidor no exceda la cantidad disponible del recurso, y al mismo tiempo use la cantidad mínima de servidores.

Esta tarea en la literatura científica se llama problema de embalaje bin (¿cómo será en ruso?). En términos simples, esta es una tarea sobre cómo insertar cajas pequeñas de tamaños arbitrarios en cajas grandes y, al mismo tiempo, usar el número mínimo de cajas grandes. El conocido problema en matemáticas, NP-complete, se resuelve con precisión solo mediante una búsqueda exhaustiva, cuyo costo está creciendo combinatoriamente.

La siguiente imagen ilustra la esencia del algoritmo de empaquetado del contenedor para el caso unidimensional:


Fig. 1. Ilustración del problema del embalaje del contenedor, ubicación no óptima

En la primera figura, los artículos se distribuyen de alguna manera entre las canastas y se usan 3 canastas para colocarlos.


Fig. 2. Ilustración del problema del embalaje del contenedor, ubicación óptima

La segunda imagen muestra la distribución óptima, para la que solo necesita 2 cestas.

La formulación estándar del algoritmo de empaque de contenedores también supone que todas las cestas son iguales. Nuestros servidores no son iguales, ya que se compraron en diferentes momentos y su configuración es diferente: diferente número de núcleos de procesador, memoria, disco, diferente potencia del procesador.

Se puede obtener una solución subóptima utilizando heurística, algoritmos genéticos, búsqueda de árboles monte-carlo y redes neuronales profundas. Nos decidimos por el algoritmo heurístico BestFit, que converge en una solución no más de 1,7 veces peor que la óptima, así como en alguna variación del algoritmo genético. A continuación daré los resultados de su aplicación.

Pero primero, analicemos qué hacer con las métricas que varían en el tiempo, como el uso de la CPU, el disco io, la red io. La forma más fácil es reemplazar la métrica variable con una constante. Pero, ¿cómo elegir el valor de esta constante? Tomamos el valor máximo de la métrica durante algún período característico (previamente suavizando los valores atípicos de los valores). La semana resultó ser un período característico en nuestro caso, ya que la principal estacionalidad en la carga se asoció con días hábiles y días libres.

En este modelo, a cada máquina virtual se le asigna una tira de recursos del tamaño del valor de recurso máximo consumido, y cada VM se describe por las constantes de uso máximo de CPU, RAM, disco, disco máximo io, red máxima io.

A continuación, utilizamos el algoritmo para calcular el empaquetamiento óptimo y obtener un mapa de la ubicación de VM en servidores físicos.

La práctica muestra que si no deja un cierto margen para cada uno de los recursos en el servidor, cuando la VM está densamente asignada, el servidor se sobrecarga. Por lo tanto, para el uso de la CPU, dejamos un margen del 30%, para la RAM del 20%, para el disco io - 20%, para la red io - 20%, estos límites se seleccionan empíricamente.

También tenemos varios tipos de discos (SSD rápidos y HDD lentos y baratos), para cada tipo de disco tomamos las métricas de disco y disco io por separado, por lo que el modelo final se vuelve algo más complicado y tiene más dimensiones.

El resultado de optimizar la colocación de VM se muestra en el diagrama:


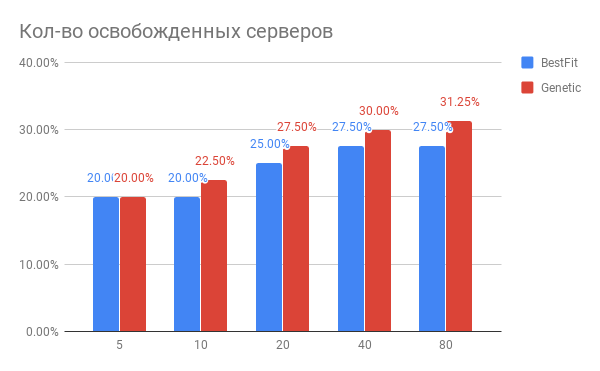Fig. 3. El resultado de optimizar la colocación de máquinas virtuales en servidores

Horizontal: el número de servidores que se han optimizado, vertical: el número de servidores liberados para la heurística BestFit y para el algoritmo genético.

¿Qué conclusiones se pueden sacar del diagrama?

1. Para las tareas actuales, puede usar 20-30% menos servidores.
2. Cuantos más servidores optimice a la vez, más ganará en%, con el número de servidores de 40 o más, se produce la saturación.
3. El algoritmo genético es ligeramente superior al heurístico BestFit. Si queremos mejorar aún más nuestros resultados, profundizaremos en esta dirección.

¿Qué otros problemas han surgido en la práctica?

1. Si desea sacudir unos 100 servidores con 7,000 máquinas virtuales, entonces el volumen de las migraciones será muy significativo, de modo que toda la idea será irrealizable. Pero si trabaja con grupos de 20-40 servidores en secuencia, el efecto que obtendrá será casi el mismo, pero la cantidad de migraciones será muchas veces menor. Y puede optimizar su DC en partes.
2. Si debe realizar migraciones en vivo, puede encontrarse con una situación en la que la migración no puede finalizar. Esto significa que dentro de la VM hay una escritura intensiva en el disco y / o el estado de los cambios de memoria, y los estados de la VM entre las réplicas antiguas y nuevas no tienen tiempo para sincronizarse hasta que cambie el estado de la réplica anterior. En este caso, debe predefinir tales máquinas VM y marcarlas como no móviles. A su vez, esto requiere la modificación de los algoritmos de optimización. Lo que agrada es que la ganancia total es prácticamente independiente del número de tales máquinas, si no hay más del 10-15% del número total de máquinas virtuales.

¿Cómo cambia la carga del servidor después de optimizar la colocación de VM?

Ok, hemos optimizado la colocación de VM. ¿Quizás el nuevo estado resultante es muy frágil en relación con el aumento de la carga? ¿Quizás los servidores están funcionando al límite y cualquier aumento en la carga los matará?

Comparamos la utilización de los recursos del servidor antes de la optimización y después durante un período de 1 semana. Lo que sucedió se muestra en la Figura 2:


Fig. 4. Cambio en la carga de la CPU después de optimizar la asignación de VM

Según el uso de la CPU: el uso promedio de la CPU ha crecido del 10% a solo el 18%. Es decir tenemos un triple margen de rendimiento de la CPU, mientras que los servidores permanecerán en la llamada zona "verde".

¿Cómo se hizo esto en el software?

Recopilamos las métricas que necesitamos en Yandex.ClickHouse (probamos InfluxDB, pero en nuestros volúmenes de datos las consultas con agregación se realizan demasiado lentamente) con una frecuencia de 30 segundos. A partir de ahí, la tarea de calcular el estado óptimo lee las métricas, calcula el consumo máximo a partir de ellas y genera una tarea de cálculo que se coloca en la cola. Tan pronto como se completa la tarea de cálculo, se ejecutan pruebas para verificar que el resultado no exceda los límites especificados.

¿Alguien ya ha hecho esto?

Según lo que conocemos, hay algoritmos similares dentro de VMware vSphere y Nutanix y aparecen dentro de OpenStack (proyecto OpenStack Watcher).

¿Es posible hacerlo aún mejor?

Si puedes. En el próximo artículo, le diré cómo empacar máquinas virtuales aún más densas sin violar el SLA, y por qué se necesitan neuronas para esto.