Al resolver los problemas de transmisión de datos a través de líneas representadas por características de frecuencia, se aplican transformadas de Fourier: la transferencia de señales del dominio del tiempo al dominio de la frecuencia y viceversa. El entorno MATLAB tiene un conjunto completo de funciones para resolver tales problemas. En este trabajo, se analiza un ejemplo de cálculo en MATLAB de la reacción de una señal transmitida a través de una línea cuya característica se mide a frecuencias que no coinciden con la frecuencia de transferencia de datos. Espero que este ejemplo facilite la comprensión de las características de la tecnología de conversión de señal en el entorno MATLAB.
Condición de la tarea
Es necesario determinar el cambio en la forma de la señal digital binaria que pasa a través del filtro y la línea de señal. La señal se establece por la amplitud y la velocidad de transmisión. El filtro de segundo orden, normalizado a la frecuencia de transferencia de datos, se establece mediante constantes de tiempo. La función de transferencia de la línea de señal está representada por la respuesta de frecuencia medida en forma compleja.
El entorno utilizado para calcular y mostrar datos es MATLAB R2015a.
Las siguientes relaciones publicadas en el sitio web
www.StatEye.org para la versión del método GUI StatEye 3.0 [1, 2, 3] se tomaron como un ejemplo de los datos iniciales.
Velocidad de datos bps = 10.3125 Gbit / s. Las constantes de tiempo del filtro de segundo orden normalizado son las mismas; su recíproco es ¾ de la frecuencia de transmisión de datos. La línea de señal está representada por una respuesta de frecuencia. La característica se midió en el canal f = 0.006495: 0.0012475: 20 GHz. El número especificado de puntos de muestreo de la transformada de Fourier: puntos = 2 ^ 13.
La Figura 1 muestra los resultados de transferencia de datos, secuencia y procesamiento de datos discutidos en este documento. La transición del dominio del tiempo al dominio de la frecuencia y viceversa se realiza utilizando el algoritmo de Transformación rápida de Fourier (FFT).
Figura 1. Canal de datos. Señal de entrada iSignal.Tx, señal de salida del filtro iSignal.Filter_out, línea de señal de salida iSignal.Rx. Las características que se muestran en el diagrama se analizan a continuación.Secuencia de cálculo
En este trabajo, los cálculos principales se realizan en el dominio de la frecuencia. Para esto, la señal original del dominio del tiempo se transfirió al dominio de la frecuencia utilizando la transformada de Fourier, al multiplicar las características espectrales de la señal, el filtro y la línea de señal, se encontró la señal de salida de la ruta, que se transfiere del dominio de la frecuencia al dominio del tiempo por la transformada inversa de Fourier.
La velocidad de transferencia de datos es dos veces mayor que la frecuencia a la que se transmiten los datos. La frecuencia máxima de la línea de señal medida máx. (Canal f) = 20 GHz. A esta frecuencia, los datos pueden transmitirse a una velocidad de 40 Gbit / s (como 2 * máx. (Canal f)).
La velocidad máxima de transferencia de datos, que no excede la velocidad máxima de transmisión en la línea de señal de 40 Gbit / sy una velocidad de transmisión múltiple de bps = 10.3125 Gbit / s, es fmax = 30.9375 Gbit / s, la multiplicidad N = 3 (N = fmax / bps). Además, fmax se usa como la frecuencia límite para calcular la respuesta de la señal usando la transformada de Fourier.
Traducción de la señal de entrada al dominio de frecuencia
Discreción de tiempo para construir la señal de entrada (bit de datos) en el dominio de tiempo Ts = 1 / fmax; Ts = 3.232e-11 s. Normalizada con respecto a la duración de la señal, la escala de tiempo consta de 2 ^ 13 puntos (puntos), la escala incluye la siguiente matriz de puntos tiempo = bps / Ts. * (1: puntos). Una señal única discreta a una velocidad de transmisión de bps = 10.3125 Gbit / sy la cuantificación con un período Ts = 1 / fmax consta de tres puntos en el rango de 10 a 11 unidades de tiempo normalizado. Se puede construir una señal de amplitud de unidad en cualquier otro lugar de la línea de tiempo, pero es mejor retroceder desde los bordes para ver completamente el fondo y el proceso de transición de la señal de salida. En la Figura 2 se muestra una señal de pulso (bit de datos) construida con los siguientes comandos de MATLAB.
iSignal.Tx(1:size(time,2)) = 0; t0 = max(find(time<=10)); t1 = max(find(time<11)); iSignal.Tx(t0:t1) = 1.0;
Figura 2. Señal de pulso de entrada iSignal.Tx, bit de datos.La traducción de la señal iSignal.Tx al dominio de frecuencia se realiza mediante las siguientes funciones FFT.
iSignal.shiftedPSD = fft(iSignal.Tx); iSignal.PSD = fftshift(iSignal.shiftedPSD);
La función de transformación de Fourier fft construye un espectro simétrico de la señal en las regiones de frecuencias positivas y negativas, cuya frecuencia máxima está en el centro del espectro (ver Figura 3). La función fftshift restaura el espectro desplazando hacia el centro la frecuencia cero de la señal como se muestra en la Figura 4.
La resolución de la frecuencia del espectro es fs = fmax / puntos; Las frecuencias del espectro varían de -fmax / 2 a fmax / 2-fs y son iguales a f = -fmax / 2: fs: fmax / 2-fs;
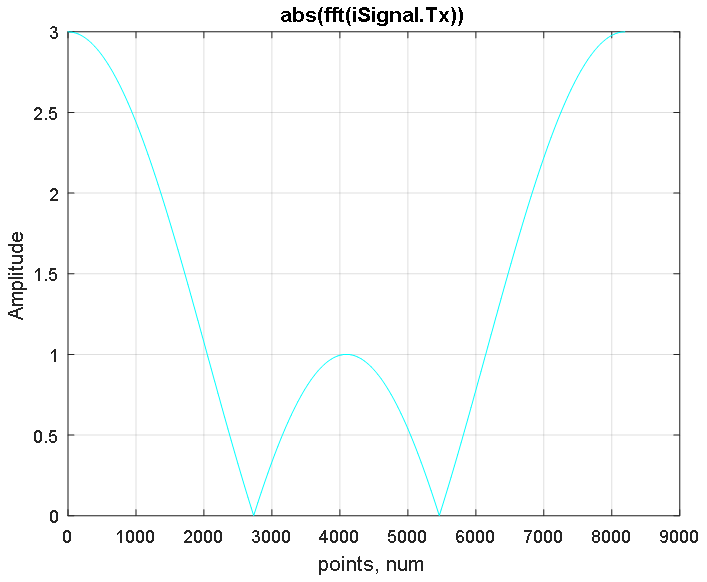Figura 3. Respuesta de amplitud del espectro desplazado de la señal iSignal.Tx obtenida utilizando la FFT.
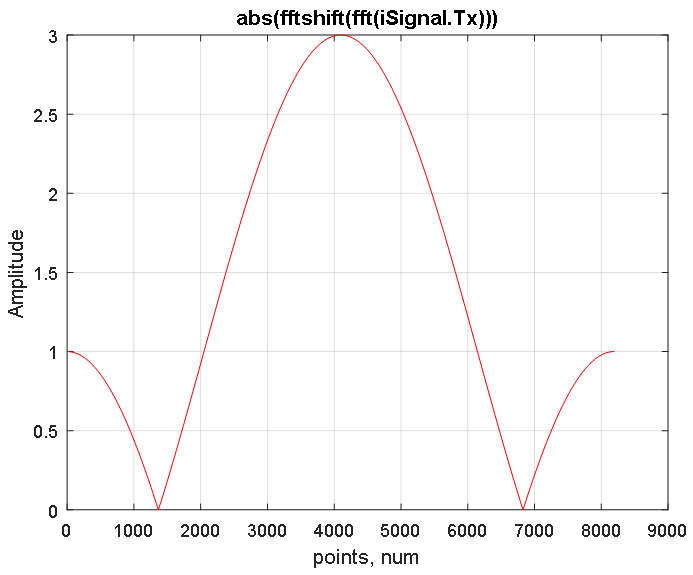Figura 4. Respuesta de amplitud del espectro reconstruido de la señal iSignal.Tx que se muestra en la Figura 3. Se presentan 2 ^ 13 muestras. El recuento promedio en 4097 corresponde a la frecuencia cero. Las frecuencias negativas se encuentran en el lado izquierdo (de 1 a 4096 puntos), y la región de frecuencias positivas en el lado derecho (de 4098 a 8192 puntos).Función de transferencia del filtro de paso bajo normalizado
En este ejemplo, la función de transferencia del filtro de segundo orden tiene la forma
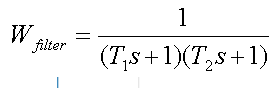
donde T1 y T2 son constantes de tiempo de filtro. Las frecuencias 1 / T1 son iguales y 1 / T2 se establecen en relación con la frecuencia a la que se transmiten los datos: 1 / T1 = 1 / T2 = 0.75 * bps (bps = 10.3125 Gbit / s).
Ancho de banda de filtro normalizado
f_nrm =fmax/bps/points.*(-points/2:points/2-1).
Operador
s = f_nrm .* j;
La característica de amplitud-fase del filtro normalizado para frecuencias positivas y negativas normalizadas con respecto a la frecuencia de transmisión de señal se muestra en la Figura 5. La característica de frecuencia de amplitud logarítmica del filtro se muestra en la Figura 6.
Figura 5. La característica de fase de amplitud de un filtro normalizado.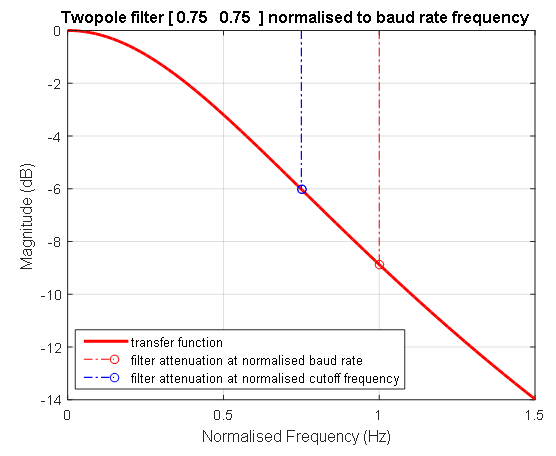
Figura 6. Respuesta de frecuencia de fase de amplitud logarítmica de un filtro normalizado. La línea discontinua azul muestra la posición de la frecuencia del filtro con un valor de 0,75 de la frecuencia a la que se transmiten los datos. A esta frecuencia (1 / T1 = 1 / T2), el coeficiente de transmisión del filtro de segundo orden es -6 decibelios. La línea roja discontinua indica la frecuencia de la unidad a la que se transmiten los datos.Traducción de los resultados de medición de la línea de señal al tipo de función de transferencia
La característica de fase de amplitud medida de la línea de señal incluye 1599 muestras en la banda de hasta 20 GHz con un paso fijo de 12.475 MHz. Contiene los siguientes valores de frecuencia: channel.f = 0.006495: 0.0012475: 20 GHz. Inicialmente, la línea de señal estaba representada por una característica de cuatro terminales. Esta característica se ha transformado y se utiliza en el ejemplo como una función compleja unidimensional.
Las frecuencias características de la línea de señal obtenidas como resultado de la medición no coinciden con las frecuencias del espectro de señal de entrada que son múltiplos de la frecuencia de transmisión de datos. Además, el espectro de la línea de señal contiene solo frecuencias positivas y no contiene frecuencias en la región cero. El espectro de la señal de entrada contiene frecuencias positivas, cero y negativas.
Para convertir las características de la línea de señal en una función de transferencia, una característica cuyas frecuencias coinciden con las frecuencias del espectro de la señal de entrada, se siguen los siguientes pasos.
1. El cálculo de la amplitud de las características de la línea a frecuencia cero mediante su extrapolación. Para esto, a partir de diez puntos de la característica de amplitud más cercana a la frecuencia cero, se encuentran los coeficientes de un polinomio lineal que se aproximan a la característica de amplitud:
[a] = polyfit(channel.f(1:10), channel.abs(1:10), 1);
El segundo coeficiente polinómico encontrado es igual a la amplitud de la característica a frecuencia cero:
channel.dc = a(2);
2. La respuesta de fase a frecuencia cero se toma igual a cero.
channel.dcPhase = 0.00;
3. El recálculo de las características de amplitud channel.abs y phase channel.phase de la línea de señal con valores a frecuencia cero se realiza en la frecuencia del espectro de señal de entrada (f = -fmax / 2: fmax / points: fmax / 2-fmax / points) con extrapolación de las características a área de frecuencias cero y negativas:
ichannel.abs = interp1([0 channel.f], [channel.dc channel.abs], abs(f), 'linear', 'extrap'); ichannel.phase = interp1([0 channel.f], [channel.dcPhase unwrap(channel.phase)], abs(f), 'linear', 'extrap'); ichannel.s = ichannel.abs .* exp(+j.*ichannel.phase); ichannel.tf = real(ichannel.s) + j*imag(ichannel.s) .* sign(f);
La función de transferencia obtenida: la respuesta de frecuencia de fase de amplitud del canal en la región de baja frecuencia se muestra en la Figura 7. Las características de frecuencia de amplitud de la línea de señal medida y la función de transferencia calculada en los rangos de frecuencia completos se muestran en la Figura 8. Las mismas características en el espacio de fase se muestran en la Figura 9.
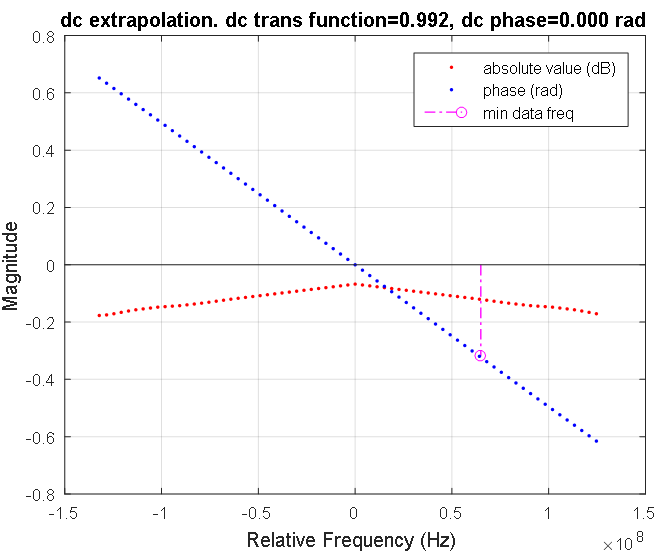Figura 7. La función de transferencia de la línea de señal en la región de baja frecuencia. Los puntos rojos y azules indican características discretas de amplitud y fase, respectivamente. La respuesta de amplitud se muestra en decibelios, la fase en radianes. La línea rosa marca la frecuencia más baja de la característica medida de la línea de señal. El coeficiente de transmisión a frecuencia cero es 0.992.
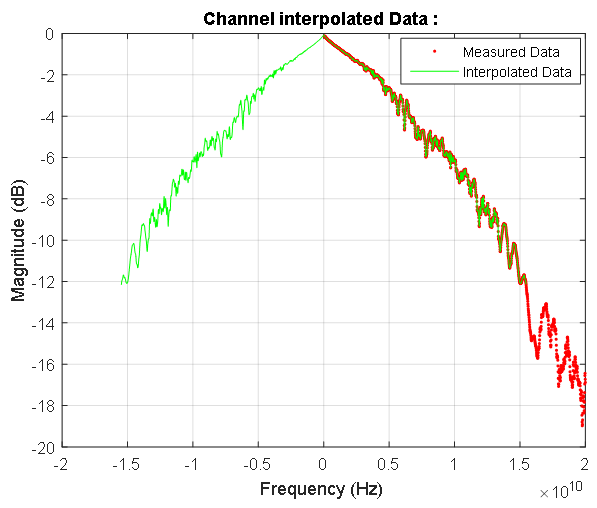Figura 8. Respuesta de frecuencia de la línea de señal. Los puntos azules indican los datos complejos de la línea medida. La dependencia simétrica calculada de la ganancia de línea de señal en las frecuencias del espectro de señal de entrada se resalta en rojo. En la región de frecuencia cero, esta característica se muestra en la Figura 7.
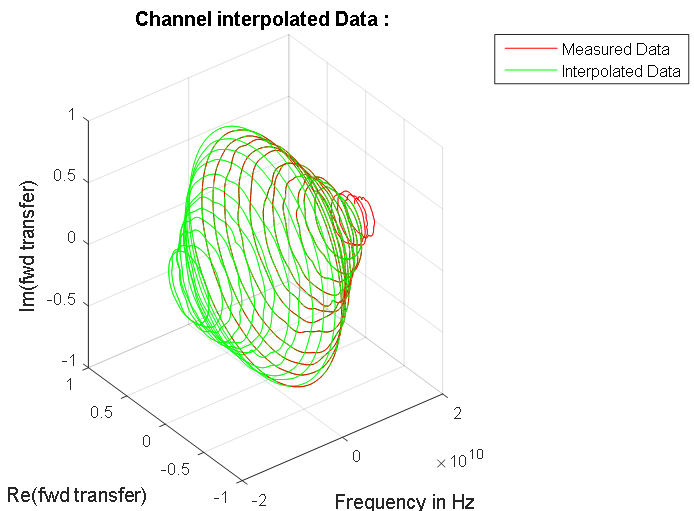Figura 9. Características de frecuencia de fase de amplitud de la línea de datos medidos y su espectro normalizado.Cálculo de respuesta de señal
La respuesta (respuesta al efecto de entrada) en el dominio de la frecuencia se obtiene multiplicando el espectro de la señal por el producto de las funciones de transferencia de los elementos que relacionan la reacción con la señal de entrada. En nuestro caso, la señal pasa a través del filtro y la línea de señal.
La transformación inversa de Fourier ifft se usa para transferir la señal del dominio de frecuencia al dominio del tiempo.
La salida del filtro en el dominio de tiempo iSignal.Filter_out se calcula como
TransFunction.PSD = iSignal.PSD .* Filter.PSD_Tx; TransFunction.shiftedPSD = ifftshift(TransFunction.PSD); iSignal.Filter_out = real(ifft(TransFunction.shiftedPSD));
La señal de salida de la línea iSignal.Rx es igual al producto del espectro de la señal de entrada y las funciones de transferencia del filtro y la línea de señal con la transferencia posterior de la señal recibida del dominio de frecuencia al dominio del tiempo.
TransFunction.PSD = TransFunction.PSD .* ichannel.tf; TransFunction.shiftedPSD = ifftshift(TransFunction.PSD); iSignal.Rx = real(ifft(TransFunction.shiftedPSD));
La respuesta del filtro al pulso ideal de entrada y la respuesta del canal se muestran en la Figura 10.
Figura 10. Salida de filtro (gráfico rojo) y salida de línea de datos (gráfico verde). Señal de entrada del filtro: en la Figura 2 se muestra un pulso único. La entrada de la línea de señal es la señal de salida del filtro.Solicitud Código m usado MATLAB
Lista bibliográfica
1. IEEE802.3ap. Resultados de la simulación NRZ de 10.3125 Gbps utilizando "StatEye" y "Modelo de señal a interferencia" en componentes de canal en cascada. Shannon Sawyer y Charles Moore / Agilent Technologies. 24 de enero de 2005
www.ieee802.org/3/ap/public/jan05/sawyer_01_0105.pdf2. Qué es StatEye. IEEE 803.3ap Task Force. 16 de septiembre de 2004
www.ieee802.org/3/ap/public/signal_adhoc/ghiasi_01_0904.pdf3. Acuerdo de Stat Eye / IBM. Steve Anderson Xilinx, Inc.
www.ieee802.org/3/ap/public/nov04/anderson_01_1104.pdf