Sostenibilidad GAN Training

La idea de GAN fue publicada por primera vez por Jan Goodfellow Generative Adversarial Nets, Goodfellow et al 2014 , después de lo cual las GAN son uno de los mejores modelos generativos.

Al igual que con cualquier otro modelo generativo, la tarea de GAN es construir un modelo de datos y, más específicamente, aprender a generar muestras de una distribución lo más cerca posible de la distribución de datos (generalmente hay un conjunto de datos de tamaño limitado en el que queremos modelar la distribución de datos).

Las GAN tienen una gran cantidad de ventajas, pero tienen un inconveniente importante: son muy difíciles de entrenar.

Recientemente, se han lanzado varios trabajos sobre sostenibilidad de GAN:

• Descenso de gradiente La optimización de GAN es localmente estable, Vaishnavh Nagarajan, J. Zico Kolter, 2017
• La Numérica de las GAN, Lars Mescheder et al, 2017

Inspirado por sus ideas, investigué un poco.

Traté de hacer el texto lo más simple posible y, si es posible, usar solo las matemáticas más simples. Desafortunadamente, para justificar por qué podemos considerar las propiedades de los campos vectoriales bidimensionales, tenemos que cavar un poco en la dirección del cálculo de las variaciones. Pero si alguien no está familiarizado con estos términos, puede proceder de forma segura inmediatamente a la consideración de campos vectoriales bidimensionales para diferentes tipos de GAN.

Ahora trataremos de mirar debajo del capó del procedimiento de capacitación y comprender lo que está sucediendo allí.

GAN, el problema principal

Las GAN consisten en dos redes neuronales: un discriminador y un generador. Generador: le permite tomar muestras de alguna distribución (generalmente llamada distribución del generador). El discriminador recibe muestras de entrada del conjunto de datos y generador originales y aprende a predecir de dónde proviene esta muestra (conjunto de datos o generador).

Esquema GAN:



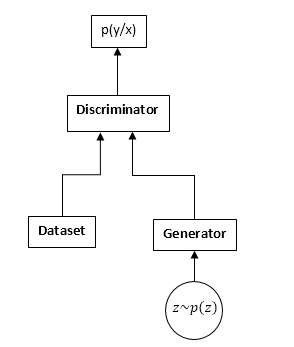
El proceso de capacitación de GAN es el siguiente:

1. Tomamos n muestras del conjunto de datos ym muestras del generador.
2. Arreglamos los pesos del generador y actualizamos los parámetros del discriminador. Esta es una tarea de clasificación común. Simplemente no necesitamos entrenar al discriminador hasta la convergencia. Y aún más a menudo también interfiere.
3. Arreglamos los pesos del discriminador y actualizamos los pesos del generador, de modo que el discriminador comienza a pensar que nuestras muestras provienen del conjunto de datos y no del generador.
4. Repetimos 1-3, hasta que el discriminador y el generador entren en equilibrio (es decir, ninguno de los otros puede "engañar" al otro).

No examinaremos en detalle el proceso de aprendizaje de GAN. En Internet, y en el hubr en particular, hay muchos artículos que explican este proceso en detalle.

Estaremos interesados ​​en algo completamente diferente. Es decir, debido al hecho de que estamos compitiendo con dos redes neuronales, la tarea deja de ser una búsqueda de un mínimo (máximo), pero se convierte en casos particulares en una búsqueda de un punto de silla de montar (es decir, en los pasos 2 y 3 intentamos lo mismo funcional maximizar por parámetros discriminadores y minimizar por parámetros del generador), y en los pasos más generales 2 y 3 podemos optimizar funcionalidades completamente diferentes. Obviamente, el problema minimax es un caso especial de optimización de diferentes funcionalidades: una funcional se toma con diferentes signos.

Veamos esto en las fórmulas. Suponemos que pd (x) es la distribución desde donde se muestrea el conjunto de datos, pg (x) es la distribución del generador, D (x) es la salida del discriminador.

Al entrenar a un discriminador, a menudo maximizamos dicha funcionalidad:

$$

$$J \ = \ \ int {p_d (x) log (D (x)) dx \ + \ \ int {p_g (x) log (1 \ - \ D (x)) dx}}$$

Vector de gradientes:

$$

$$v = \ \ nabla_ \ theta J \ = \ int {\ frac {p_d (x)} {D (x)} \ nabla_ \ theta D (x) \ dx \ + \ \ int {\ frac {p_g (x )} {1 \ - \ D (x)} \ nabla_ \ theta D (x) dx}}$$

Al entrenar al generador, maximizamos:

$$

$$I \ = \ - \ int {p_g (x) log (1 \ - \ D (x)) dx}$$

El vector de gradientes en este caso:

$$

$$u \ = \ \ nabla_ \ varphi I \ = \ - \ int {{\ nabla_ \ varphi p} _g (x) log (1 \ - \ D (x)) dx}$$

En el futuro, veremos que los funcionales pueden ser reemplazados respectivamente por:

$$

$$J \ = \ \ int {p_d (x) f_1 (D (x)) dx \ + \ \ int {p_g (x) f_2 (D (x)) dx}}$$

$$

$$I \ = \ \ int {p_g (x) f_3 (D (x)) dx}$$

Donde $$$f_1, f_2, f_3$ son seleccionados de acuerdo con ciertas reglas. Por cierto, Ian Goodfellow utiliza en su artículo original $$$f_1 y f_2$ como cuando se entrena a un discriminador regular, y $$$f_3$ elige para mejorar los gradientes en la etapa inicial de capacitación:

$$

$$f_1 \ left (x \ right) = log \ left (x \ right), \ f_2 \ left (x \ right) = log \ left (1 \ - \ x \ right), f_3 \ left (x \ right) = log \ left (x \ right)$$

A primera vista, la tarea parecería ser muy similar a la tarea habitual de aprender con el gradiente de descenso (ascenso). ¿Por qué, entonces, todos los que se encontraron con el entrenamiento de GAN estuvieron de acuerdo en que fue tan difícil?

La respuesta se encuentra en la estructura del campo vectorial, que usamos para actualizar los parámetros de las redes neuronales. En el caso del problema de clasificación habitual, usamos solo el vector de gradiente, es decir, el campo es potencial (el funcional optimizado en sí mismo es el potencial de este campo vectorial). Y los campos vectoriales potenciales tienen algunas propiedades notables, una de las cuales es la ausencia de curvas cerradas. Es decir, es imposible caminar en círculos en este campo. Pero al entrenar GAN, a pesar del hecho de que los campos vectoriales para el generador y el discriminador son potenciales por separado (los mismos son gradientes), el campo vectorial total no será potencial. Y esto significa que en este campo puede haber curvas cerradas, es decir, podemos caminar en círculos. Y esto es muy, muy malo.

Surge la pregunta: ¿por qué, de todos modos, logramos entrenar a la GAN con bastante éxito, tal vez el campo todavía es irritable (potencial)? Y si es así, ¿por qué es tan complicado?
Voy a seguir adelante, desafortunadamente, el campo no es potencial, pero tiene una serie de buenas propiedades. Desafortunadamente, el campo también es muy sensible a la parametrización de redes neuronales (la elección de funciones de activación, el uso de DropOut, BatchNormalization, etc.). Pero lo primero es lo primero.

Campo GAN "Gradiente"

Consideraremos las funcionalidades de aprendizaje de GAN en la forma más general:

$$

$$J \ = \ \ int {p_d (x) f_1 (D (x)) dx \ + \ \ int {p_g (x) f_2 (D (x)) dx}}$$

$$

$$I \ = \ \ int {p_g (x) f_3 (D (x)) dx}$$

Necesitamos optimizar ambas funcionalidades al mismo tiempo. Suponiendo que D (x) y pg (x) son funciones absolutamente flexibles, es decir Podemos tomar cualquier número en cualquier punto, independientemente de otros puntos. Ese es un hecho bien conocido del cálculo de variaciones: debe cambiar la función en la dirección de la derivada variacional de esta función (en general, un análogo completo del aumento del gradiente).

Escribimos la derivada variacional:

$$

$$\ frac {\ partial J} {\ partial D (x)} = p_d (x) f_1 '(D (x)) \ + \ p_g (x) f_2' (D (x))$$

$$

$$\ frac {\ partial I} {\ partial p_g (x)} = f_3 (D (x))$$

Consideraremos solo el primer funcional (para el discriminador), para el segundo todo será igual.

Pero considerando que, de hecho, podemos cambiar la función solo en el conjunto de funciones que son representables por nuestra red neuronal, escribiremos:

$$$$ display $$ ∆D (x) = \ frac {\ partial D (x)} {\ partial θ_j} Δθ_j $$ display $$

cambios en los parámetros de la red, en general, el descenso de gradiente habitual (aumento):

$$$$ display $$ ∆θj = \ frac {\ partial J} {\ partial θ_j} μ $$ display $$

µ es la tasa de aprendizaje. Bueno, la derivada con respecto a los parámetros de red:

$$

$$\ frac {\ partial J} {\ partial \ theta_j} = \ int {\ frac {\ partial J} {\ partial D (y)} \ frac {\ partial D (y)} {\ partial \ theta_j} dy }$$

Y ahora lo estamos poniendo todo junto:

$$

$$∆D (x) = \ sum_ {j} {\ frac {\ partial D (x)} {\ partial \ theta_j} \ int {\ frac {\ partial J} {\ partial D (y)} \ frac { \ partial D (y)} {\ partial \ theta_j} dy} \ mu \ = \ mu \ int \ frac {\ partial J} {\ partial D (y)}} \ sum_ {j} {\ frac {\ partial D (x)} {\ partial \ theta_j} \ frac {\ partial D (x)} {\ partial \ theta_j} dy \ = \} \ mu \ int {\ frac {\ partial J} {\ partial D (y )} K_ \ theta (x, y) dy}$$

Donde: $$$K_ \ theta (x, y) \ = \ sum_ {j} {\ frac {\ partial D (x)} {\ partial \ theta_j} \ frac {\ partial D (x)} {\ partial \ theta_j} \ }$

Nunca he visto esta característica en la literatura sobre aprendizaje automático, por lo que lo llamaré el núcleo paramétrico del sistema.

Bueno, o si vamos a pasos continuos en el tiempo (desde ecuaciones de diferencia a diferenciales), obtenemos:

$$

$$\ frac {d} {dt} D (x) \ = \ \ int {\ frac {\ partial J} {\ partial D (y)} K_ \ theta (x, y) dy}$$

Esta ecuación muestra la relación interna del campo original (puntiagudo para el discriminador) y la parametrización de la red neuronal. Obtenemos una ecuación completamente similar para el generador.

Dado que K (x, y) (el núcleo paramétrico) es una función definida positiva (bueno, ¿cómo puede representarse como un producto escalar de gradientes en los puntos correspondientes?), Podemos concluir que cualquier cambio en las funciones entrenadas (discriminador y generador) pertenece al espacio de Hilbert generado por el núcleo, es decir K (x, y). Me pregunto si es posible obtener resultados significativos aquí. Pero todavía no miraremos en esa dirección, sino que miraremos en la otra.

Como puede ver, la estabilidad de la GAN está determinada por dos componentes: las derivadas variacionales de los funcionales y la parametrización de la red neuronal. Nuestra tarea es ver cómo este campo se comporta puntualmente, es decir, si nuestra red puede representar absolutamente cualquier función. La tarea se convierte en un análisis de un campo vectorial bidimensional. Y esto, creo, está en nuestro poder.

Sostenibilidad

Entonces, consideramos el siguiente campo vectorial:

$$

$$\ frac {d} {dt} D (x) = \ \ frac {\ partial J} {\ partial D (x)}$$

$$

$$\ frac {d} {dt} p_g (x) = \ \ frac {\ partial I} {\ partial p_g (x)}$$

Obviamente, estas ecuaciones pueden considerarse solo para un punto x, teniendo en cuenta cómo se ven nuestras derivadas variacionales:

$$

$$\ frac {d} {dt} D = \ p_df_1 ^ \ prime (D) \ + \ p_gf_2 ^ \ prime (D)$$

$$

$$\ frac {d} {dt} p_g \ = \ f_3 (D)$$

El primer requisito para este sistema de ecuaciones es que los lados derechos deben ir a 0 cuando:
$$$p_d = p_g$

De lo contrario, intentaremos entrenar el modelo, que obviamente no convergerá a la solución correcta. Es decir D debe ser una solución a la siguiente ecuación:

$$

$$f_1 ^ \ prime (D) \ + \ f_2 ^ \ prime (D) \ = \ 0$$

Denotamos esta solución como $$$D0$ .

Dado el hecho de que pg (x) es la densidad de probabilidad en el lado derecho, podemos agregar cualquier número sin violar las derivadas. Para proporcionar 0 del lado derecho en el punto deseado, reste el valor en t. $$$D0$ (esto debe hacerse si queremos considerar pg pointwise: la transición de un campo parametrizado por densidades de probabilidad a campos libres).

Como resultado, obtenemos el siguiente campo:

$$

$$\ frac {d} {dt} D = \ p_df_1 ^ \ prime (D) \ + \ p_gf_2 ^ \ prime (D)$$

$$

$$\ frac {d} {dt} p_g \ = \ f_3 (D) \ - \ f (D0)$$

A partir de ahora, estudiaremos los puntos inactivos y la estabilidad de los campos de este tipo.
Podemos estudiar dos tipos de estabilidad: local (en la vecindad del punto de reposo) y global (utilizando el método de la función de Lyapunov).

Para estudiar la estabilidad local, es necesario calcular la matriz de Jacobi del campo.
Para que el campo sea localmente “estable” es necesario que los valores propios tengan una parte real negativa.

Diferentes tipos de GAN

1. GAN clásico

   
   
   En la GAN clásica, usamos logloss regular:
   

   $$

   $$J \ = \ \ int {p_d (x) log (D (x)) dx \ + \ \ int {p_g (x) log (1 \ - \ D (x)) dx}}$$
   
   Para el entrenamiento del discriminador, es necesario maximizarlo; para el generador, minimizarlo. En este caso, el campo se verá así:
   

   $$

   $$\ frac {d} {dt} D = \ \ frac {p_d} {D} \ - \ \ frac {p_g} {1-D}$$
   
   

   $$

   $$\ frac {d} {dt} p_g \ = \ -log (1-D) \ + \ log (\ frac {1} {2})$$
   
   Veamos cómo evolucionarán los parámetros (pg y D) en este campo. Para hacer esto, use este simple script de Python:
   
   
   Guión

   def get_v(d, pg, pd): vd = pd/d - pg/(1.-d) vpg = -np.log(1.-d) + np.log(0.5) return vd, vpg d = 0.75 pg = 0.9 pd = 0.2 d_hist = [] pg_hist = [] lr = 1e-3 n_iter = 100000 for i in range(n_iter): d_hist.append(d) pg_hist.append(pg) vd, vpg = get_v(d, pg, pd) d = d + lr*vd pg = pg + lr*vpg plt.plot(d_hist, pg_hist, '-') plt.show() 

   
   
   
   Para punto de partida $$$p_g = 0.9, D = 0.25$ se verá así:
   
   
   
   El punto de descanso de dicho campo será: pg = pd y D = 0.5
   
   Se puede verificar fácilmente que las partes reales de los valores propios de la matriz de Jacobi son negativas, es decir, el campo es localmente estable.
   No trataremos con la prueba de la sostenibilidad global. Pero si es muy interesante, puede jugar con el script de Python y asegurarse de que el campo sea estable para cualquier valor inicial válido.

2. Modificación por Jan Goodfellow

   
   Ya discutimos anteriormente que Ian Goodfellow en el artículo original usó una versión ligeramente modificada de GAN. Para su versión, las funciones fueron las siguientes:
   

   $$

   $$f_1 \ left (x \ right) = log \ left (x \ right), \ f_2 \ left (x \ right) = log \ left (1 \ - \ x \ right), f_3 \ left (x \ right) = log \ left (x \ right)$$
   
   El campo se verá así:
   

   $$

   $$\ frac {d} {dt} D = \ \ frac {p_d} {D} \ - \ \ frac {p_g} {1-D}$$
   
   

   $$

   $$\ frac {d} {dt} p_g \ = \ log (D) \ - \ log (\ frac {1} {2})$$
   
   El script de Python será el mismo, solo que la función de campo es diferente:
   
   
   Guión

    def get_v(d, pg, pd): vd = pd/d - pg/(1.-d) vpg = np.log(d) - np.log(0.5) return vd, vpg d = 0.75 pg = 0.9 pd = 0.2 d_hist = [] pg_hist = [] lr = 1e-3 n_iter = 100000 for i in range(n_iter): d_hist.append(d) pg_hist.append(pg) vd, vpg = get_v(d, pg, pd) d = d + lr*vd pg = pg + lr*vpg plt.plot(d_hist, pg_hist, '-') plt.show() 

   
   
   
   Y con los mismos datos iniciales, la imagen se ve así:
   
   
   
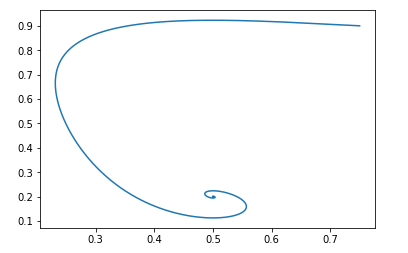
   Y nuevamente, es fácil verificar que el campo será localmente estable.
   Es decir, desde el punto de vista de la convergencia, dicha modificación no perjudica las propiedades de la GAN, pero tiene sus propias ventajas en términos de entrenamiento de redes neuronales.

3. Wasserstein gan

   
   Veamos otra vista popular de GAN. La funcionalidad optimizada se ve así:
   

   $$

   $$J \ = \ \ int {p_d (x) D (x) dx \ - \} \ int {p_g (x) D (x) dx}$$
   
   Donde D pertenece a la clase de funciones 1-Lipschitz con respecto a x.
   Queremos maximizarlo en D y minimizarlo en pg.
   
   Obviamente, en este caso: $$$f_1 \ left (x \ right) = x, \ f_2 \ left (x \ right) = - x, \ f_3 \ left (x \ right) = x$
   
   Y el campo se verá así:
   

   $$

   $$\ frac {d} {dt} D = \ p_d \ - {\ p} _g \ $$
   
   

   $$

   $$\ frac {d} {dt} p_g \ = \ D$$
   
   En este campo, se adivina fácilmente un círculo con un centro en un punto. $$$p_g = p_d, D = 0$ .
   Es decir, si vamos por este campo, siempre daremos vueltas en círculos.
   
   Aquí hay un ejemplo de una trayectoria en dicho campo:
   
   
   
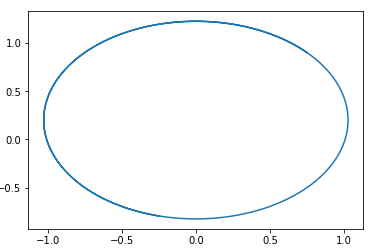
   La pregunta es, ¿por qué entonces resulta entrenar este tipo de GAN? La respuesta es muy simple: este análisis no tiene en cuenta el hecho de la propiedad 1-Lipschitz de D. Es decir, no podemos tomar funciones arbitrarias. Por cierto, esto está de acuerdo con los resultados de los autores ... del artículo. Para evitar caminar en círculo, recomiendan entrenar al discriminador para que converja: Wasserstein GAN

4. Nuevas opciones de GAN

   
   Selección de funciones $$$f_1, f_2 y f_3$ Puede crear diferentes opciones de GAN. El requisito principal para estas funciones es asegurar la presencia de un punto de reposo "correcto" y la estabilidad de este punto (preferiblemente global, pero al menos local). Le doy al lector la oportunidad de deducir las restricciones sobre las funciones f1, f2 y f3, necesarias para la estabilidad local. Es fácil: solo considere la ecuación cuadrática para los valores propios de la matriz de Jacobi.
   
   Daré un ejemplo de tal GAN:
   

   $$

   $$f_1 (x) \ = \ -0.5x ^ 2, \ f_2 (x) \ = \ x, \ f_3 (x) \ = \ -x$$
   
   Nuevamente, sugiero que el lector mismo construya el campo de esta GAN y demuestre su estabilidad. (Por cierto, este es uno de los pocos campos para los que la evidencia de la estabilidad global es elemental: solo seleccione la función Lyapunov, la distancia al punto de reposo). Solo tenga en cuenta que el punto de descanso es D = 1.

Conclusión y más investigación.

Del análisis anterior se puede ver que todas las GAN clásicas (con la excepción de Wassertein GAN, que tiene sus propios métodos para mejorar la estabilidad) tienen campos "buenos". Es decir El seguimiento de estos campos tiene un único punto de reposo en el que la distribución del generador es igual a la distribución de datos.

¿Por qué, entonces, entrenar a GAN es una tarea tan difícil? La respuesta es simple: parametrización de redes neuronales. Con una parametrización "mala", también podemos hacer caminatas en círculos. Por ejemplo, mis experimentos muestran que, por ejemplo, usar BatchNormalization en cualquiera de las redes convierte inmediatamente el campo en cerrado. Y la activación de Relu funciona mejor.

Desafortunadamente, por el momento no hay una sola forma de verificar teóricamente qué elementos de la red neuronal cómo cambiar el campo. Me resultará prospectivo investigar las propiedades del núcleo paramétrico del sistema: $$$K_ \ theta (x, y)$ .

También quería hablar sobre formas de regularizar los campos GAN y analizar esto desde la perspectiva de los campos bidimensionales. Considere los algoritmos de aprendizaje de refuerzo desde esta perspectiva. Y mucho mas. Pero desafortunadamente, el artículo resultó ser demasiado grande de todos modos, así que más sobre eso en otro momento.