Las redes neuronales profundas han llevado a un gran avance en muchas tareas de reconocimiento de imágenes, como la visión por computadora y el reconocimiento de voz. La red neuronal convolucional es uno de los tipos populares de redes neuronales.
Básicamente, una red neuronal convolucional puede considerarse como una red neuronal que utiliza muchas copias idénticas de la misma neurona. Esto permite que la red tenga un número limitado de parámetros cuando se computan modelos grandes.
 Red neuronal convolucional 2D
Red neuronal convolucional 2DEsta técnica con varias copias de la misma neurona tiene una analogía cercana con la abstracción de funciones en matemáticas y ciencias de la computación. Durante la programación, la función se escribe una vez y luego se reutiliza, sin requerir que escriba el mismo código muchas veces en diferentes lugares, lo que acelera la ejecución del programa y reduce la cantidad de errores. Del mismo modo, una red neuronal convolucional, una vez que ha entrenado una neurona, la usa en muchos lugares, lo que facilita el entrenamiento del modelo y minimiza los errores.
La estructura de las redes neuronales convolucionales.
Supongamos que se da una tarea en la que se requiere predecir a partir del audio si hay una voz de persona en el archivo de audio.
En la entrada, obtenemos muestras de audio en diferentes momentos. Las muestras se distribuyen uniformemente.

La forma más fácil de clasificarlos con una red neuronal es conectar todas las muestras a una capa totalmente conectada. En este caso, cada entrada está conectada a cada neurona.
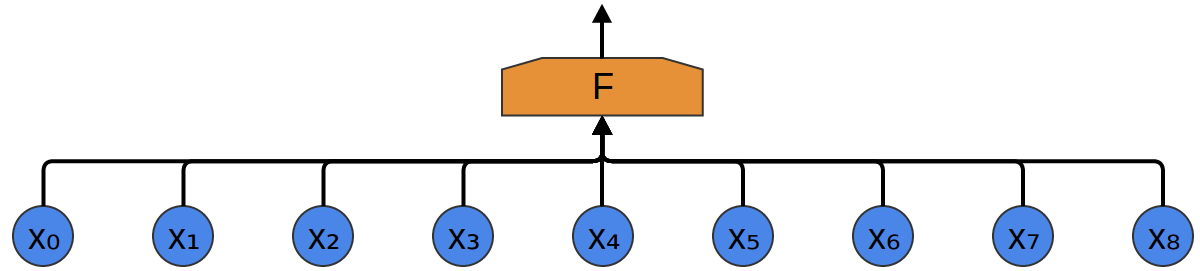
Un enfoque más complejo tiene en cuenta cierta simetría en las propiedades que se encuentran en los datos. Prestamos mucha atención a las propiedades locales de los datos: ¿cuál es la frecuencia del sonido durante un tiempo determinado? ¿Aumentando o disminuyendo? Y así sucesivamente.
Tenemos en cuenta las mismas propiedades en todo momento. Es útil conocer las frecuencias al principio, a la mitad y al final. Tenga en cuenta que estas son propiedades locales, ya que solo necesita una pequeña ventana de secuencia de audio para definirlas.
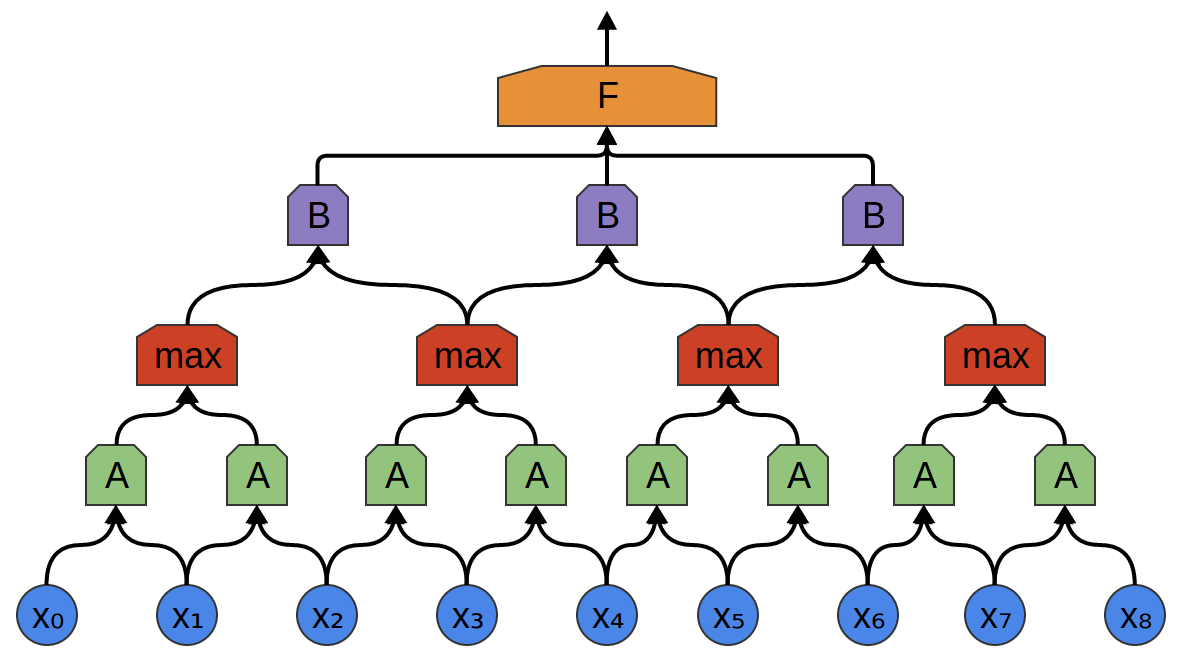
Por lo tanto, es posible crear un grupo de neuronas A, que consideran pequeños segmentos de tiempo en nuestros datos. A observa todos estos segmentos, calculando ciertas funciones. Luego, la salida de esta capa convolucional se alimenta a una capa F. completamente conectada.
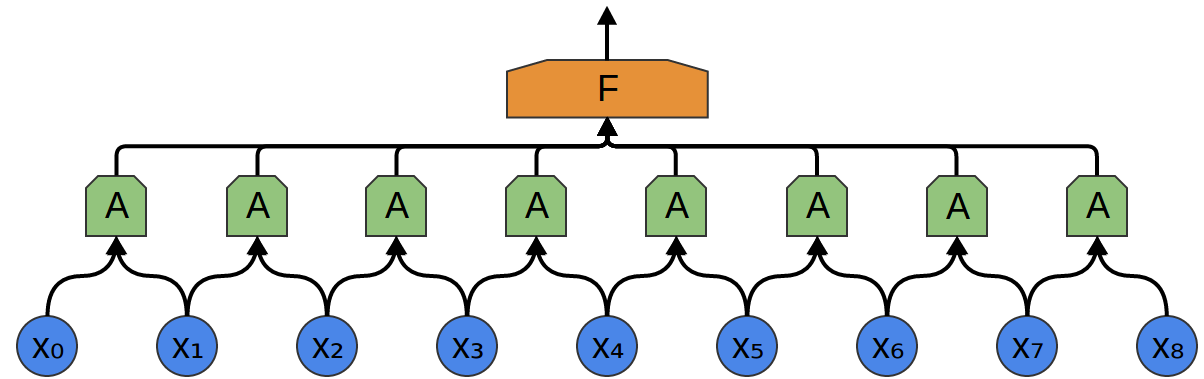
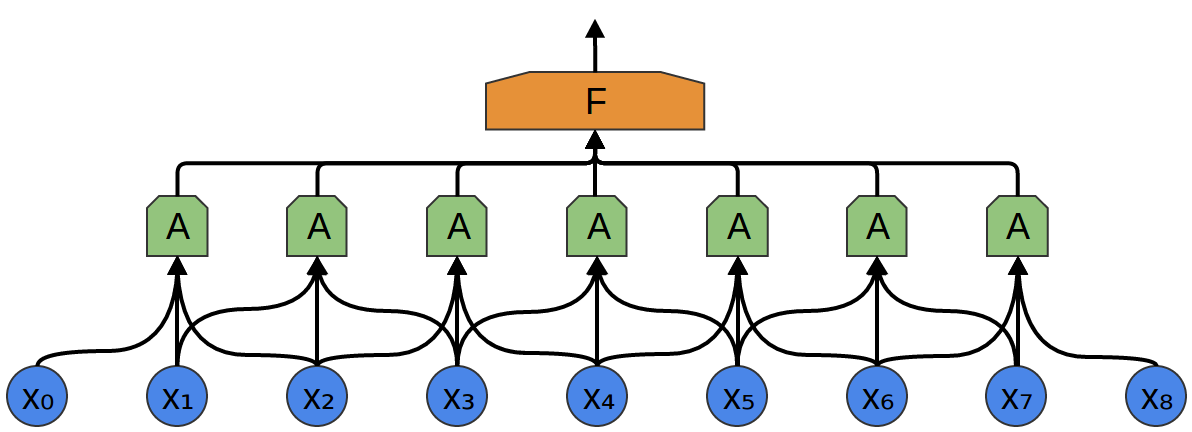
En el ejemplo anterior, A procesó solo segmentos de dos puntos. Esto es raro en la práctica. Por lo general, la ventana de capa de convolución es mucho más grande.
En el siguiente ejemplo, A recibe 3 segmentos en la entrada. Esto también es poco probable para las tareas del mundo real, pero, desafortunadamente, es difícil visualizar A conectando múltiples entradas.
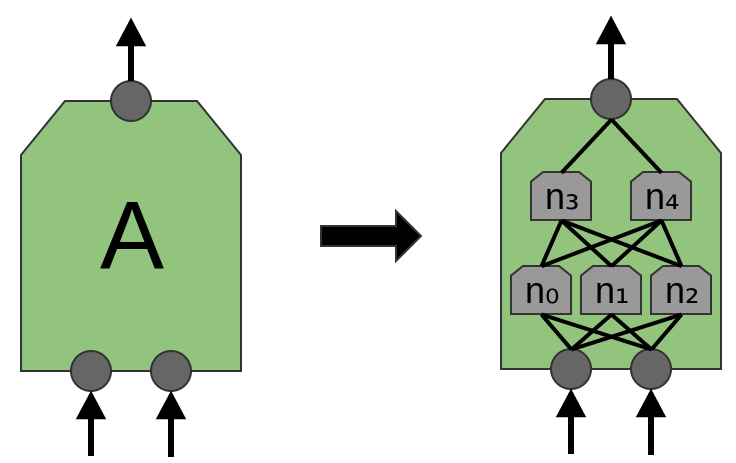
Una buena propiedad de las capas convolucionales es que son compuestas. Puede alimentar la salida de una capa convolucional a otra. Con cada capa, la red descubre funciones más altas y más abstractas.
En el siguiente ejemplo, hay un nuevo grupo de neuronas B. B se usa para crear otra capa convolucional colocada encima de la anterior.
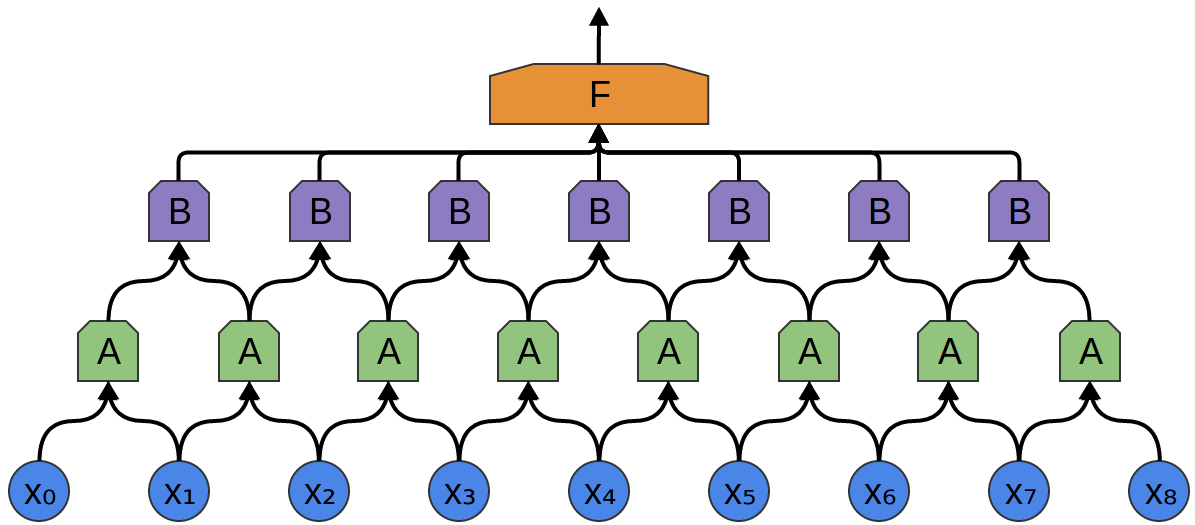
Las capas convolucionales a menudo se entrelazan agrupando (combinando) capas. En particular, hay un tipo de capa llamada max-pooling, que es extremadamente popular.
A menudo, no nos importa el momento exacto en el tiempo cuando una señal útil está presente en los datos. Si un cambio en la frecuencia de la señal ocurre tarde o temprano, ¿importa?
La agrupación máxima absorbe características máximas de pequeños bloques del nivel anterior. La conclusión dice si la señal de la función deseada estaba presente en la capa anterior, pero no exactamente dónde.
Capas de agrupación máxima: esta es una "disminución". Permite que las capas convolucionales posteriores funcionen en grandes piezas de datos, porque los pequeños parches después de la capa de fusión corresponden al parche mucho más grande frente a él. También nos hacen invariables a algunas transformaciones de datos muy pequeñas.
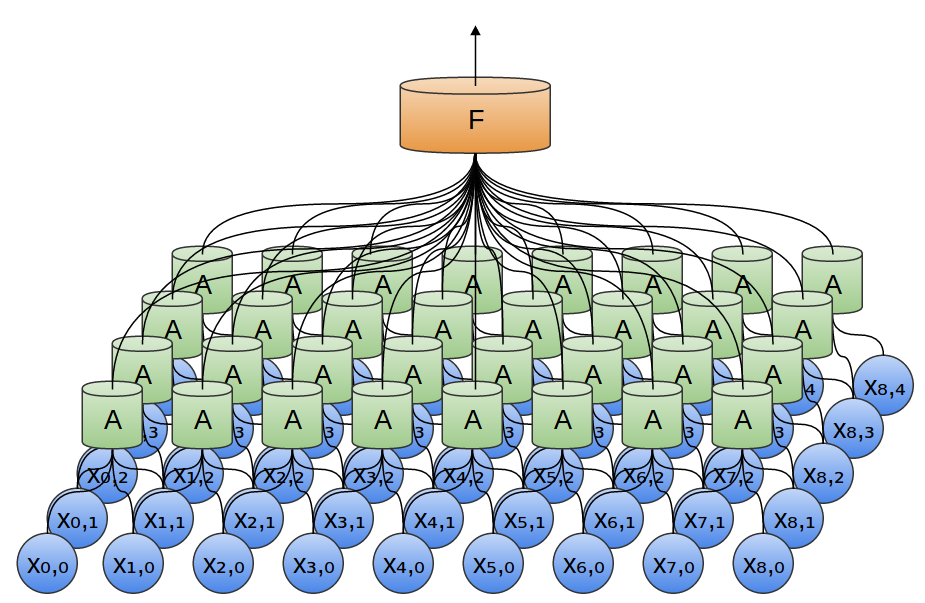
En nuestros ejemplos anteriores, se utilizaron capas convolucionales unidimensionales. Sin embargo, las capas convolucionales pueden funcionar con datos más voluminosos. De hecho, las soluciones más famosas basadas en redes neuronales convolucionales utilizan redes neuronales convolucionales bidimensionales para el reconocimiento de patrones.
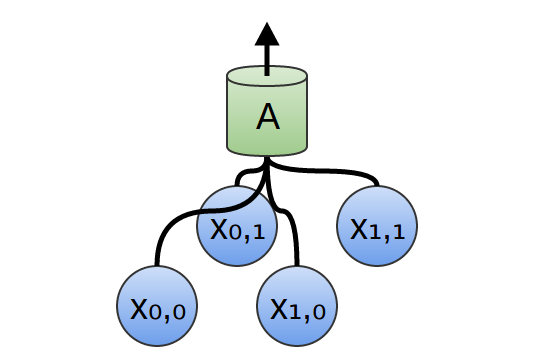
En una capa convolucional bidimensional, en lugar de mirar segmentos, A observará parches.
Para cada parche, A calculará la función. Por ejemplo, ella puede aprender a detectar la presencia de un borde, o textura, o el contraste entre dos colores.
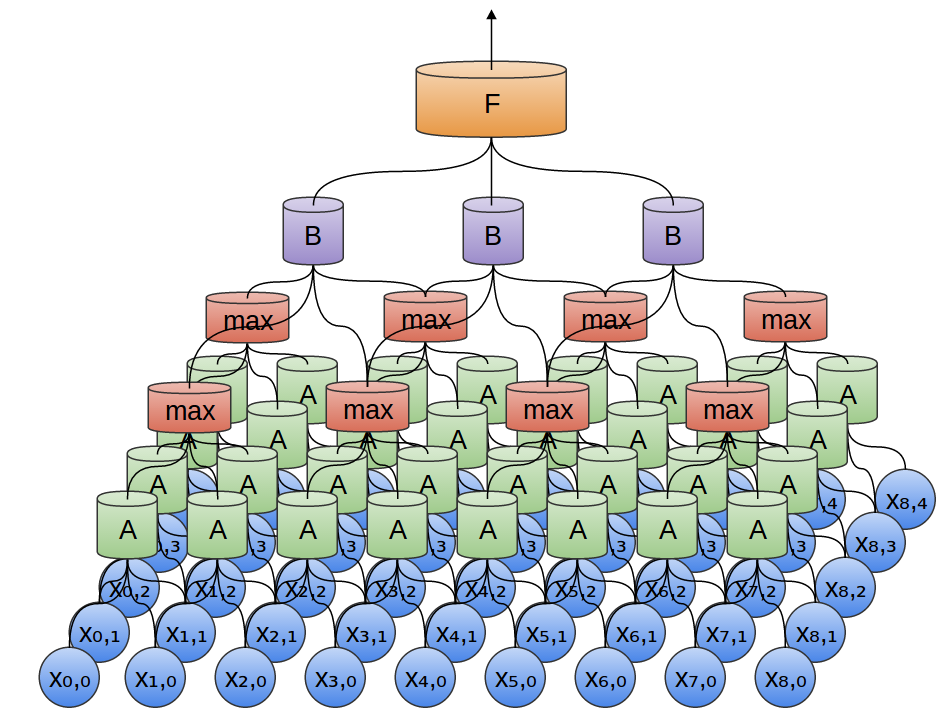
En el ejemplo anterior, la salida de la capa convolucional se introdujo en una capa totalmente conectada. Pero, es posible componer dos capas convolucionales, como fue el caso en el caso unidimensional considerado.

También podemos realizar la agrupación máxima en dos dimensiones. Aquí tomamos el máximo de características de un pequeño parche.
Esto se reduce al hecho de que cuando se considera la imagen completa, la posición exacta del borde, hasta el píxel, no es importante. Es suficiente saber dónde se encuentra dentro de unos pocos píxeles.
Además, las redes de convolución tridimensionales a veces se usan para datos como video o datos masivos (por ejemplo, escaneo 3D en medicina). Sin embargo, tales redes no son muy utilizadas y son mucho más difíciles de visualizar.
Anteriormente, dijimos que A es un grupo de neuronas. Seremos más precisos en eso: ¿qué es A?
En las capas convolucionales tradicionales, A es un conjunto paralelo de neuronas, todas las neuronas reciben las mismas señales de entrada y calculan diferentes funciones.
Por ejemplo, en una capa convolucional bidimensional, una neurona puede detectar bordes horizontales, otra, bordes verticales y un tercer contraste de color verde-rojo.
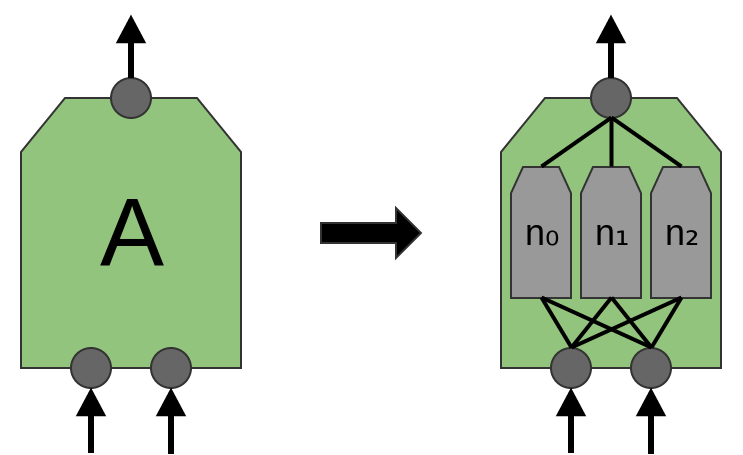
El artículo 'Red en Red' (Lin et al. (2013)) propone una nueva capa, "Mlpconv". En este modelo, A tiene varios niveles de neuronas, y la última capa deriva funciones de nivel superior para la región que se está tratando. En el artículo, el modelo logra resultados impresionantes, estableciendo un nuevo nivel de tecnología en una serie de conjuntos de datos de referencia.
A los fines de esta publicación, nos centraremos en las capas convolucionales estándar.
Resultados de la red neuronal convolucional
En 2012, Alex Krizhevsky, Ilya Sutskever y Geoff Hinton lograron una mejora significativa en la calidad del reconocimiento en comparación con las soluciones conocidas en ese momento (Krizehvsky et al. (2012)).
El progreso fue el resultado de combinar varios enfoques. Los procesadores gráficos se utilizaron para entrenar una red neuronal profunda (según los estándares de 2012). Se utilizó un nuevo tipo de neurona (ReLU) y una nueva técnica para reducir el problema llamado "sobreajuste" (DropOut). Utilizamos un gran conjunto de datos con una gran cantidad de categorías de imágenes (ImageNet). Y, por supuesto, era una red neuronal convolucional.
La arquitectura que se muestra a continuación era profunda. Tiene 5 capas convolucionales, 3 agrupaciones alternas y tres capas completamente conectadas.
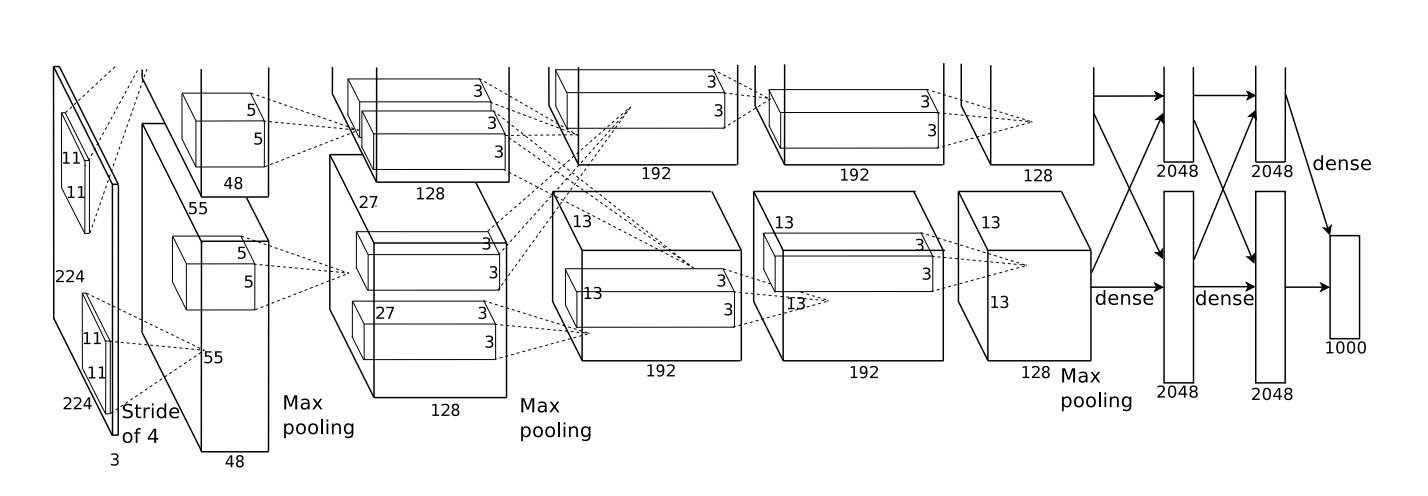
De Krizehvsky et al. (2012)
La red ha sido entrenada para clasificar fotos en miles de categorías diferentes.
El modelo de Krizhevsky et al. Fue capaz de dar la respuesta correcta en el 63% de los casos. Además, la respuesta correcta de las 5 mejores respuestas, ¡hay un 85% de pronósticos!

Permítanos ilustrar lo que reconoce el primer nivel de la red.
Recordemos que las capas convolucionales se dividieron entre dos GPU. La información no va y viene a través de cada capa. Resulta que cada vez que se inicia el modelo, ambos lados se especializan.

Filtros obtenidos por la primera capa convolucional. La mitad superior corresponde a una capa en una GPU, la mitad inferior en la otra. De Krizehvsky et al. (2012)
Las neuronas de un lado se enfocan en blanco y negro, aprendiendo a detectar bordes de diferentes orientaciones y tamaños. Las neuronas, por otro lado, se especializan en color y textura, detectan contrastes y patrones de color. Recuerde que las neuronas se inicializan al azar. Ni una sola persona fue y los estableció como detectores fronterizos, o los dividió de esta manera. Esto sucedió mientras entrenaba la red de clasificación de imágenes.
Estos resultados notables (y otros resultados interesantes a lo largo del tiempo) fueron solo el comienzo. Fueron seguidos rápidamente por muchos otros trabajos que probaron enfoques modificados y mejoraron gradualmente los resultados o los aplicaron en otras áreas.
Las redes neuronales convolucionales son una herramienta importante en la visión por computadora y el reconocimiento de patrones modernos.
Formalización de redes neuronales convolucionales.
Considere una capa convolucional unidimensional con entradas {xn} y salidas {yn}:
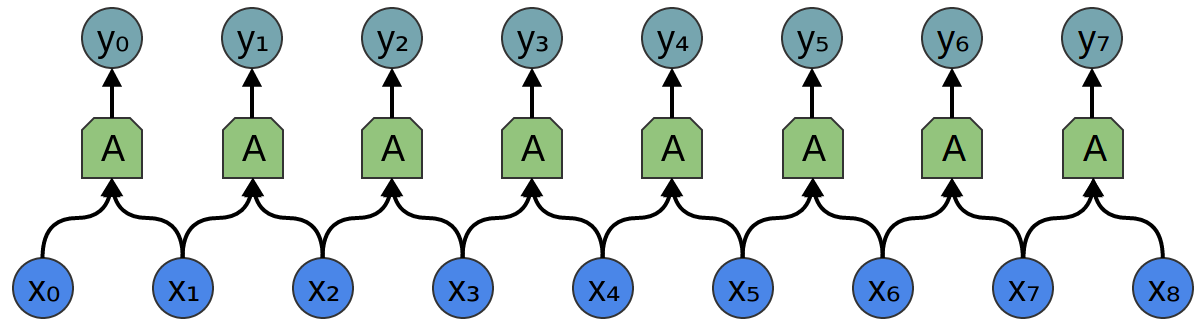
Es relativamente fácil describir los resultados en términos de entrada:
yn = A (x, x + 1, ...)
Por ejemplo, en el ejemplo anterior:
y0 = A (x0, x1)
y1 = A (x1, x2)
Del mismo modo, si consideramos una capa convolucional bidimensional con entradas {xn, m} y salidas {yn, m}:
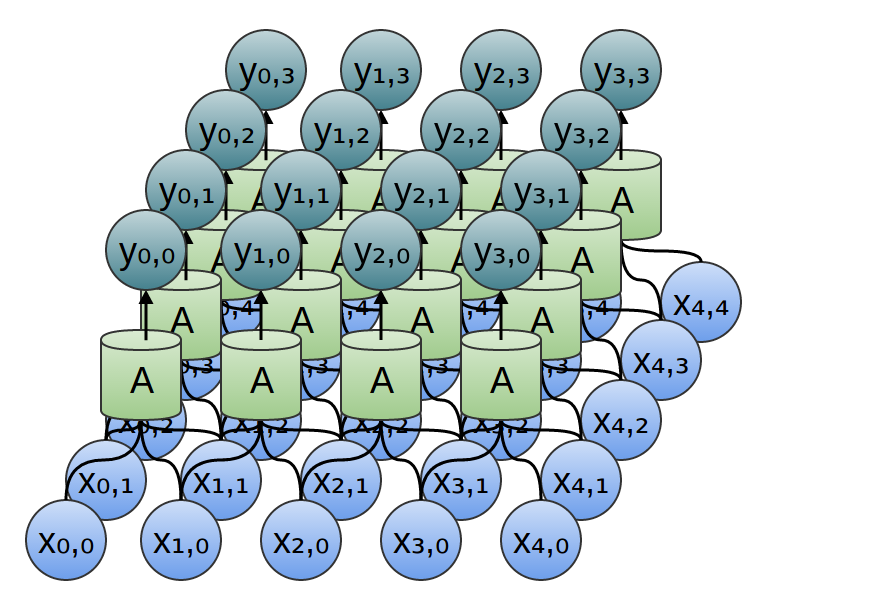
La red se puede representar mediante una matriz de valores bidimensional.
Conclusión
La operación de convolución es una herramienta poderosa. En matemáticas, la operación de convolución surge en diferentes contextos, desde el estudio de ecuaciones diferenciales parciales hasta la teoría de probabilidades. En parte debido a su papel en PDE, la convolución es importante en las ciencias físicas. La convolución también juega un papel importante en muchas áreas de aplicación, como gráficos por computadora y procesamiento de señales.