Durante muchos años he estado viendo el billar como un deporte. Lo tiene todo: la fascinante belleza de un juego intelectual, la elegancia de los golpes de kiem y la tensión psicológica de la competencia. Pero hay una cosa que no me gusta: su sistema de calificación .
Su principal inconveniente es que solo tiene en cuenta el hecho del logro del torneo sin tener en cuenta la "complejidad" de los partidos. El modelo Elo se ve privado de este inconveniente, que controla la "fuerza" de los jugadores y lo actualiza según los resultados de los partidos y la "fuerza" del oponente. Sin embargo, no encaja perfectamente: se cree que todos los partidos se llevan a cabo en igualdad de condiciones, y en el billar se juegan hasta cierto número de cuadros ganados (partidos). Para dar cuenta de este hecho, consideré otro modelo, al que llamé EloBeta .
Este artículo estudia la calidad de los modelos Elo y EloBet en función de los resultados de los partidos de billar. Es importante tener en cuenta que los objetivos principales son evaluar la "fuerza" de los jugadores y crear una calificación "justa", en lugar de construir modelos predictivos para obtener ganancias.

La calificación actual del billar se basa en los logros del jugador en torneos con su "peso" diferente. Érase una vez, solo se tuvieron en cuenta los Campeonatos del Mundo. Después de la aparición de muchas otras competiciones, se desarrolló una tabla de puntos que el jugador podría ganar cuando llegara a una determinada etapa del torneo. Ahora la calificación tiene la forma de una cantidad "móvil" de premios que el jugador ha ganado durante los (aproximadamente) últimos dos años calendario.
Este sistema tiene dos ventajas principales: es simple (gana mucho dinero - sube en el ranking) y predecible (si quieres subir a un cierto lugar - gana una cierta cantidad de dinero, todas las demás cosas son iguales). El problema es que con este método no se tiene en cuenta la fuerza (habilidad, forma) de los oponentes . El contraargumento habitual es: "Si un jugador ha llegado a la última etapa del torneo, entonces él / ella es, por definición, el jugador fuerte actual" ("los jugadores débiles no ganan torneos"). Suena bastante convincente. Sin embargo, en el billar, como en cualquier deporte, el papel del caso debe tenerse en cuenta: si un jugador es "más débil", esto no significa que él / ella nunca pueda ganar "más fuerte" en un partido contra un jugador. Simplemente sucede con menos frecuencia que el escenario inverso. Aquí es donde el modelo Elo entra en escena.
La idea del modelo Elo es que cada jugador está asociado con una calificación numérica. Se introduce una suposición de que el resultado de un juego entre dos jugadores puede predecirse en función de la diferencia en sus clasificaciones: valores más altos significan una mayor probabilidad de ganar un jugador "fuerte" (con una calificación más alta). La calificación Elo se basa en la "fuerza" actual , calculada sobre la base de los resultados de los partidos con otros jugadores. Esto evita una falla importante en el sistema de calificación oficial actual. Este enfoque también le permite actualizar la calificación del jugador durante el torneo para responder numéricamente a su buen desempeño.
Al tener experiencia práctica con la calificación Elo, me parece que debería mostrarse bien en el billar. Sin embargo, hay un obstáculo: está diseñado para competiciones con un solo tipo de partido . Por supuesto, hay variaciones para tener en cuenta las ventajas del campo local en el fútbol y el primer movimiento en el ajedrez (ambos en forma de agregar un número fijo de puntos de calificación al jugador con una ventaja). En el billar, los partidos se juegan en el formato "mejor de N": el jugador que gana los primeros gana n= fracN+12 marcos (fiestas). También llamaremos a este formato "hasta n victorias ".
Intuitivamente, ganar un partido de hasta 10 victorias (final de un torneo serio) debería ser más difícil para un jugador "débil" que ganar un partido de 4 victorias (primera ronda de los torneos nacionales actuales). Esto se tiene en cuenta en mi modelo EloBet .
La idea de usar la calificación Elo en el billar no es nueva. Por ejemplo, hay los siguientes trabajos:
- Snooker Analyst utiliza un sistema de calificación "Elo like" (más como un modelo Bradley - Terry ). La idea es actualizar la calificación en función de la diferencia entre el número "real" y "esperado" de cuadros ganados. Este enfoque plantea preguntas. Por supuesto, la mayor diferencia en el número de cuadros probablemente demuestre la mayor diferencia en fuerza, pero inicialmente el jugador no tiene esa tarea. En el billar, el objetivo es "solo" ganar el partido, es decir Gana un cierto número de fotogramas antes que el oponente.
- Esta discusión está en el foro con la implementación del modelo básico de Elo.
- Este y estos son usos reales en el snooker amateur.
- Quizás hay otros trabajos que me perdí. Estaría muy agradecido por cualquier información sobre este tema.
Revisar
Este artículo está destinado a usuarios del lenguaje R que estén interesados en estudiar la calificación de Elo, y para los fanáticos del snooker. Todos los experimentos están escritos con la idea de ser reproducibles. El código está oculto bajo spoilers, tiene comentarios y utiliza paquetes tidyverse , por lo que puede ser interesante para los usuarios leer por sí mismos R. Se supone que todo el código presentado se ejecuta secuencialmente. Un archivo se puede encontrar aquí .
El artículo está organizado de la siguiente manera:
- La sección Modelo describe los enfoques de Elo y EloBet con implementación en R.
- La sección Experimento describe los detalles y la motivación del cálculo: qué datos y metodología se utilizan (y por qué), y qué resultados se obtienen.
- La sección Estudio de clasificación EloBet contiene los resultados de la aplicación del modelo EloBet a datos reales de billar. Estará más interesado en los amantes del snooker.
Necesitaremos la siguiente inicialización.
Código de inicialización# suppressPackageStartupMessages(library(dplyr)) library(tidyr) library(purrr) # library(ggplot2) # suppressPackageStartupMessages(library(comperank)) theme_set(theme_bw()) # . . set.seed(20180703)
Modelos
Ambos modelos se basan en los siguientes supuestos:
- Hay un conjunto fijo de jugadores que deben clasificarse de "más fuerte" (primer lugar) a "más débil" (último lugar).
- Clasificación por asociación de jugadores i con calificación numérica ri : Un número que representa la "fuerza" del jugador (un valor más alto significa un jugador más fuerte).
- Cuanto mayor sea la diferencia en las calificaciones antes del partido, menos probable es la victoria del jugador "débil" (con una calificación más baja).
- Las calificaciones se actualizan después de cada partido en función de su resultado y las calificaciones anteriores.
- Una victoria sobre un oponente "más fuerte" debe ir acompañada de un aumento mayor en la calificación que una victoria sobre un oponente "más débil". Con la derrota, lo contrario es cierto.
Elo
Código modelo Elo #' @details . #' `...` . #' #' @return , 1 ( `rating1`) #' 2 ( `rating2`). #' . elo_win_prob <- function(rating1, rating2, ksi = 400, ...) { norm_rating_diff <- (rating2 - rating1) / ksi 1 / (1 + 10^norm_rating_diff) } #' @return , #' `comperank::add_iterative_ratings()`. elo_fun_gen <- function(K, ksi = 400) { function(rating1, score1, rating2, score2) { comperank::elo(rating1, score1, rating2, score2, K = K, ksi = ksi)[1, ] } }
Elo Model actualiza las calificaciones mediante el siguiente procedimiento:
Cálculo de la probabilidad de que cierto jugador gane el partido (antes de que comience). La probabilidad de que un jugador gane (lo llamaremos "primero") con el identificador i y calificado ri sobre otro jugador ("segundo") con identificador j y calificado rj es igual
Pr(ri,rj)= frac11+10(rj−ri)/400
Con este enfoque, el cálculo de la probabilidad obedece al tercer supuesto.
Normalizar la diferencia a 400 es una forma matemática de decir qué diferencia se considera "grande". Este número puede ser reemplazado con un parámetro modelo. xi Sin embargo, esto solo afecta la propagación de calificaciones futuras y generalmente es redundante. Un valor de 400 es bastante estándar.
Con un enfoque general, la probabilidad de victoria es igual L(rj−ri) donde L(x) alguna función estrictamente creciente con valores de 0 a 1. Usaremos la curva logística. Un estudio más completo se puede encontrar en este artículo .
Cálculo del resultado del partido S . En el modelo base, es igual a 1 en caso de victoria del primer jugador (derrota del segundo), 0.5 en caso de empate y 0 en caso de derrota del primer jugador (victoria del segundo).
Actualización de calificación :
- delta=K cdot(S−Pr(ri,rj)) . Esta es la cantidad por la cual cambiarán las calificaciones. Ella usa un coeficiente K (el único parámetro del modelo). Menos K (con probabilidades iguales) significa un cambio menor en las calificaciones: el modelo es más conservador, es decir Se necesitan más victorias para "probar" un cambio de fuerza. Por otro lado, más K significa más credibilidad con resultados recientes que calificaciones actuales. La elección de "óptimo" K es una forma de crear un "buen" sistema de calificación .
- r(nuevo)i=ri+ delta , r(nuevo)j=rj− delta .
Observaciones :
- Como se puede ver en las fórmulas de actualización, la suma de las calificaciones de todos los jugadores considerados no cambia con el tiempo: la calificación aumenta debido a una disminución en la calificación del oponente
- Los jugadores sin partidos jugados están asociados con una calificación inicial de 0. Por lo general, se utilizan valores de 1500 o 1000, pero no veo otra razón que psicológica. Teniendo en cuenta el comentario anterior, usar cero significa que la suma de todas las calificaciones siempre es cero, lo cual es hermoso a su manera.
- Es necesario jugar un cierto número de partidos para que la calificación refleje la "fuerza" del jugador. Esto presenta un problema: los jugadores recién agregados comienzan con una calificación de 0, que probablemente no sea la más pequeña entre los jugadores actuales. En otras palabras, los "recién llegados" se consideran "más fuertes" que algunos otros jugadores. Puede intentar combatir esto con procedimientos de actualización de calificación externa al ingresar a un nuevo jugador.
¿Por qué tiene sentido un algoritmo así? En caso de igualdad de calificaciones delta siempre es igual 0.5 cdotK . Supongamos, por ejemplo, que ri=0 y rj=400 . Esto significa que la probabilidad de ganar el primer jugador es frac11+10 aproximadamente0.0909 es decir él / ella ganará 1 partido de 11.
- En caso de victoria, él / ella recibirá un aumento de aproximadamente 0.909 cdotK , que es más que en el caso de la igualdad de calificaciones.
- En caso de una derrota, él / ella recibirá una reducción de aproximadamente 0.0909 cdotK , que es menor que en el caso de igualdad de calificaciones.
Esto muestra que el modelo Elo obedece a la quinta suposición: una victoria sobre un oponente es "más fuerte" se acompaña de un aumento mayor en la calificación que una victoria sobre un oponente es "más débil", y viceversa.
Por supuesto, el modelo Elo tiene sus propias características prácticas (de alto nivel). Sin embargo, lo más importante para nuestro estudio es lo siguiente: se supone que todos los partidos se llevan a cabo en igualdad de condiciones. Esto significa que la distancia del partido no se tiene en cuenta: una victoria en un partido de hasta 4 victorias se recompensa de la misma manera que una victoria en un partido de hasta 10 victorias. Aquí viene el modelo de escenario EloBeta.
EloBeta
Código de modelo EloBet #' @details . #' #' @return , 1 ( `rating1`) #' 2 ( `rating2`). `frames_to_win` #' . #' . elobeta_win_prob <- function(rating1, rating2, frames_to_win, ksi = 400, ...) { prob_frame <- elo_win_prob(rating1 = rating1, rating2 = rating2, ksi = ksi) # , `frames_to_win` # # (`prob_frame`). . pbeta(prob_frame, frames_to_win, frames_to_win) } #' @return : 1 / #' (), 0.5 0 / (). get_match_result <- function(score1, score2) { # () , . near_score <- dplyr::near(score1, score2) dplyr::if_else(near_score, 0.5, as.numeric(score1 > score2)) } #' @return , #' `add_iterative_ratings()`. elobeta_fun_gen <- function(K, ksi = 400) { function(rating1, score1, rating2, score2) { prob_win <- elobeta_win_prob( rating1 = rating1, rating2 = rating2, frames_to_win = pmax(score1, score2), ksi = ksi ) match_result <- get_match_result(score1, score2) delta <- K * (match_result - prob_win) c(rating1 + delta, rating2 - delta) } }
En el modelo Elo, la diferencia en las calificaciones afecta directamente la probabilidad de ganar la partida completa. La idea principal del modelo EloBet es la influencia directa de la diferencia en las calificaciones sobre la probabilidad de ganar en un cuadro y el cálculo explícito de la probabilidad de que un jugador gane n marcos antes del oponente .
La pregunta sigue siendo: ¿cómo calcular tal probabilidad? Resulta que este es uno de los problemas más antiguos en la historia de la teoría de la probabilidad y tiene su propio nombre: el problema de dividir las apuestas (Problema de puntos). Una muy buena presentación se puede encontrar en este artículo . Usando su notación, la probabilidad deseada es:
P(n,n)= sum limits2n−1j=n2n−1 choosejpj(1−p)2n−1−j
Aqui P(n,n) - probabilidad de que el primer jugador gane el partido antes n victorias p - la probabilidad de su victoria en un cuadro (el oponente tiene probabilidad 1−p ) Con este enfoque, se supone que los resultados del cuadro dentro de la coincidencia son independientes entre sí . Esto puede estar en duda, pero es una suposición necesaria para este modelo.
¿Hay una forma más rápida de calcular? Resulta que la respuesta es sí. Después de varias horas de conversión de fórmulas, experimentos prácticos y búsquedas en Internet, encontré la siguiente propiedad en una función beta incompleta regularizada Ix(a,b) . Sustituyendo m=k, n=2k−1 en esta propiedad y reemplazando k en n resulta P(n,n)=Ip(n,n) .
Esto también es una buena noticia para los usuarios de R, ya que Ip(n,n) se puede calcular como pbeta(p, n, n) . Nota : el caso general de la probabilidad de victoria en n fotogramas antes de que el oponente gane m también se puede calcular como Ip(n,m) y pbeta(p, n, m) respectivamente. Esto abre grandes oportunidades para actualizar la probabilidad de ganar durante el partido .
El procedimiento de actualización de calificación en el marco del modelo EloBet tiene el siguiente formulario (con calificaciones conocidas ri y rj cantidad de cuadros necesarios para ganar n y el resultado del partido S , como en el modelo Elo):
- Cálculo de la probabilidad de victoria del primer jugador en un cuadro : p=Pr(ri,rj)= frac11+10(rj−ri)/400 .
- Cálculo de la probabilidad de victoria de este jugador en el partido : PrBeta(ri,rj)=Ip(n,n) . Por ejemplo, si p igual a 0.4, entonces la probabilidad de ganar el partido antes de 4 victorias cae a 0.29, y en "a 18 victorias" - a 0.11.
- Actualización de calificación :
- delta=K cdot(S−PrBeta(ri,rj)) .
- r(nuevo)i=ri+ delta , r(nuevo)j=rj− delta .
Nota : porque la diferencia en las calificaciones afecta directamente la probabilidad de ganar en un cuadro, y no en todo el partido, se debe esperar un valor de coeficiente óptimo más bajo K : parte del valor delta proviene de un efecto de refuerzo PrBeta(ri,rj) .
La idea de calcular el resultado de un partido basado en la probabilidad de ganar en un cuadro no es muy nueva. En este sitio de autoría de François Labelle , puede encontrar un cálculo en línea de la probabilidad de ganar el "mejor de N "Coincide, junto con otras funciones. Me alegré de ver que nuestros resultados de cálculo coinciden. Sin embargo, no pude encontrar ninguna fuente para introducir un enfoque de este tipo en el procedimiento de actualización para las calificaciones Elo. Como antes, estaré muy agradecido por cualquier información sobre este tema.
Solo pude encontrar este artículo y la descripción del sistema Elo en el servidor de juegos de backgammon (FIBS). También hay un análogo en ruso . Aquí, se tienen en cuenta las diferentes duraciones de los partidos al multiplicar la diferencia en las calificaciones por la raíz cuadrada de la distancia del partido. Sin embargo, no parece tener ninguna justificación teórica.
Un experimento
Un experimento tiene varios objetivos. Según los resultados de los partidos de billar:
- Determinar los mejores valores de coeficientes K para ambos modelos
- Estudiar la estabilidad de los modelos en términos de precisión de la probabilidad predictiva.
- Para estudiar el efecto del uso de torneos de "invitación" en las clasificaciones.
- Cree un historial de clasificación justo para la temporada 2017/18 para todos los jugadores profesionales.
Datos
Código de generación de datos de experimento # "train", "validation" "test" split_cases <- function(n, props = c(0.5, 0.25, 0.25)) { breaks <- n * cumsum(head(props, -1)) / sum(props) id_vec <- findInterval(seq_len(n), breaks, left.open = TRUE) + 1 c("train", "validation", "test")[id_vec] } pro_players <- snooker_players %>% filter(status == "pro") # pro_matches_all <- snooker_matches %>% # filter(!walkover1, !walkover2) %>% # semi_join(y = pro_players, by = c(player1Id = "id")) %>% semi_join(y = pro_players, by = c(player2Id = "id")) %>% # 'season' left_join( y = snooker_events %>% select(id, season), by = c(eventId = "id") ) %>% # arrange(endDate) %>% # widecr transmute( game = seq_len(n()), player1 = player1Id, score1, player2 = player2Id, score2, matchId = id, endDate, eventId, season, # ("train", "validation" "test") # 50/25/25 matchType = split_cases(n()) ) %>% # widecr as_widecr() # (, # , Championship League). pro_matches_off <- pro_matches_all %>% anti_join( y = snooker_events %>% filter(type == "Invitational"), by = c(eventId = "id") ) # get_split <- . %>% count(matchType) %>% mutate(share = n / sum(n)) # 50/25/25 (train/validation/test) pro_matches_all %>% get_split() ## # A tibble: 3 x 3 ## matchType n share ## <chr> <int> <dbl> ## 1 test 1030 0.250 ## 2 train 2059 0.5 ## 3 validation 1029 0.250 # , # . , # __ __, `pro_matches_all`. # , __ # __. pro_matches_off %>% get_split() ## # A tibble: 3 x 3 ## matchType n share ## <chr> <int> <dbl> ## 1 test 820 0.225 ## 2 train 1810 0.497 ## 3 validation 1014 0.278 # K k_grid <- 1:100
Utilizaremos los datos de billar del paquete comperank . La fuente original es snooker.org . Los resultados se toman de los siguientes partidos:
- El partido se jugó en la temporada 2016/17 o 2017/18 .
- El partido es parte de un torneo de billar "profesional" , es decir:
- Es del tipo "Invitational", "Qualifying" o "Ranking". También distinguiremos dos juegos de partidos: "todos los partidos" (de todos los datos del torneo) y "partidos oficiales" (excluyendo torneos de invitación). Hay dos razones para esto:
- En los torneos de invitación, no todos los jugadores tienen la oportunidad de cambiar su calificación. Esto no es necesariamente malo en el marco de los modelos Elo y EloBet, pero tiene un "tinte de injusticia".
- Existe la creencia de que los jugadores "se toman en serio" solo para las clasificaciones oficiales. Nota : la mayoría de los torneos por invitación forman parte de la Championship League, que creo que es aceptada por la mayoría de los jugadores.
no muy en serio en forma de práctica con la capacidad de ganar dinero. La presencia de estos torneos puede afectar el ranking. Además de la "Championship League" hay otros torneos de invitación: "2016 China Championship", ambos "Champion of Champions", ambos "Masters", "2017 Hong Kong Masters", "2017 World Games", "2017 Romanian Masters".
- Describe un billar tradicional (no 6 rojos o Power Snooker) entre jugadores individuales (no equipos).
- Ambos sexos pueden estar involucrados (no solo hombres o mujeres).
- Pueden participar jugadores de todas las edades (no solo personas mayores o "menores de 21 años").
- Esto no es un "Shoot-Out" porque estos torneos se almacenan en la base de datos snooker.org.
- El partido realmente tuvo lugar : su resultado es el resultado de un juego real que involucra a ambos jugadores.
- El partido se celebra entre dos profesionales . La lista de profesionales se toma para la temporada 2017/18 (131 jugadores). Esta decisión parece ser la más controvertida, ya que la eliminación de partidos que involucran "ciegos" de aficionados a la derrota de profesionales de aficionados. Esto lleva a una ventaja injusta de estos jugadores. Me parece que tal decisión es necesaria para reducir la inflación de la calificación que se producirá al tener en cuenta los partidos con aficionados. Otro enfoque es estudiar profesionales y aficionados juntos, pero esto parece irracional en el marco de este estudio. La derrota de un aficionado profesional se considera una pérdida de la oportunidad de aumentar la calificación.
El número final de partidos utilizados es 4118 para "todos los partidos" y 3644 para "partidos oficiales" (62.9 y 55.6 por jugador, respectivamente).
Metodología
Código de función de experimento #' @param matches `longcr` `widecr` `matchType` #' ( : "train", "validation" "test"). #' @param test_type . #' #' ("") . , #' `game`. #' @param k_vec K . #' @param rate_fun_gen , K #' `add_iterative_ratings()`. #' @param get_win_prob #' (`rating1`, `rating2`) , #' (`frames_to_win`). ____: #' . #' @param initial_ratings #' `add_iterative_ratings()`. #' #' @details : #' - `matches` #' `game`. #' - `test_type`: #' - 1. #' - : 1 / #' (), 0.5 0 / (). #' - RMSE: , #' "" - . #' #' @return Tibble 'k' K 'goodness' #' RMSE. compute_goodness <- function(matches, test_type, k_vec, rate_fun_gen, get_win_prob, initial_ratings = 0) { cat("\n") map_dfr(k_vec, function(cur_k) { # cat(cur_k, " ") matches %>% arrange(game) %>% add_iterative_ratings( rate_fun = rate_fun_gen(cur_k), initial_ratings = initial_ratings ) %>% left_join(y = matches %>% select(game, matchType), by = "game") %>% filter(matchType %in% test_type) %>% mutate( # framesToWin = pmax(score1, score2), # 1 `framesToWin` winProb = get_win_prob( rating1 = rating1Before, rating2 = rating2Before, frames_to_win = framesToWin ), result = get_match_result(score1, score2), squareError = (result - winProb)^2 ) %>% summarise(goodness = sqrt(mean(squareError))) }) %>% mutate(k = k_vec) %>% select(k, goodness) } #' `compute_goodness()` compute_goodness_wrap <- function(matches_name, test_type, k_vec, rate_fun_gen_name, win_prob_fun_name, initial_ratings = 0) { matches_tbl <- get(matches_name) rate_fun_gen <- get(rate_fun_gen_name) get_win_prob <- get(win_prob_fun_name) compute_goodness( matches_tbl, test_type, k_vec, rate_fun_gen, get_win_prob, initial_ratings ) } #' #' #' @param test_type `test_type` ( ) #' `compute_goodness()`. #' @param rating_type ( ). #' @param data_type . #' @param k_vec,initial_ratings `compute_goodness()`. #' #' @details #' . #' , , #' : #' - "pro_matches_" + `< >` + `< >` . #' - `< >` + "_fun_gen" . #' - `< >` + "_win_prob" , #' . #' #' @return Tibble : #' - __testType__ <chr> : . #' - __ratingType__ <chr> : . #' - __dataType__ <chr> : . #' - __k__ <dbl/int> : K. #' - __goodness__ <dbl> : . do_experiment <- function(test_type = c("validation", "test"), rating_type = c("elo", "elobeta"), data_type = c("all", "off"), k_vec = k_grid, initial_ratings = 0) { crossing( testType = test_type, ratingType = rating_type, dataType = data_type ) %>% mutate( dataName = paste0("pro_matches_", testType, "_", dataType), kVec = rep(list(k_vec), n()), rateFunGenName = paste0(ratingType, "_fun_gen"), winProbFunName = paste0(ratingType, "_win_prob"), initialRatings = rep(list(initial_ratings), n()), experimentData = pmap( list(dataName, testType, kVec, rateFunGenName, winProbFunName, initialRatings), compute_goodness_wrap ) ) %>% unnest(experimentData) %>% select(testType, ratingType, dataType, k, goodness) }
"" K K=1,2,...,100 . , . :
- K :
- . , .
add_iterative_ratings() comperank . " ", .. . - , ( ) , . RMSE ( ) ( ). , RMSE=√1|T|∑t∈T(St−Pt)2 donde T — , |T| — , St — , Pt — ( ). , " " .
- Valor K RMSE . "" , RMSE K ( ). 0.5 ( "" 0.5) .
, : "train" (), "validation" () "test" (). , .. "train"/"validation" , "validation"/"test". 50/25/25 " ". " " " " . : 49.7/27.8/22.5. , , .
:
- : .
- : " " " " ( ". ").
- : "" ( "validation" RMSE "" "train" ) "" ( "test" RMSE "" "train" "validation" ).
Resultados
pro_matches_validation_all <- pro_matches_all %>% filter(matchType != "test") pro_matches_validation_off <- pro_matches_off %>% filter(matchType != "test") pro_matches_test_all <- pro_matches_all pro_matches_test_off <- pro_matches_off
# experiment_tbl <- do_experiment()
plot_data <- experiment_tbl %>% unite(group, ratingType, dataType) %>% mutate( testType = recode( testType, validation = "", test = "" ), groupName = recode( group, elo_all = ", ", elo_off = ", . ", elobeta_all = ", ", elobeta_off = ", . " ), # groupName = factor(groupName, levels = unique(groupName)) ) compute_optimal_k <- . %>% group_by(testType, groupName) %>% slice(which.min(goodness)) %>% ungroup() compute_k_labels <- . %>% compute_optimal_k() %>% mutate(label = paste0("K = ", k)) %>% group_by(groupName) %>% # K , # . - # . mutate(hjust = - (k == max(k)) * 1.1 + 1.05) %>% ungroup() plot_experiment_results <- function(results_tbl) { ggplot(results_tbl) + geom_hline( yintercept = 0.5, colour = "#AA5555", size = 0.5, linetype = "dotted" ) + geom_line(aes(k, goodness, colour = testType)) + geom_vline( data = compute_optimal_k, mapping = aes(xintercept = k, colour = testType), linetype = "dashed", show.legend = FALSE ) + geom_text( data = compute_k_labels, mapping = aes(k, Inf, label = label, hjust = hjust), vjust = 1.2 ) + facet_wrap(~ groupName) + scale_colour_manual( values = c(`` = "#377EB8", `` = "#FF7F00"), guide = guide_legend(title = "", override.aes = list(size = 4)) ) + labs( x = " K", y = " (RMSE)", title = " ", subtitle = paste0( ' ( ) ', ' .\n', ' K ( ', '"") , .' ) ) + theme(title = element_text(size = 13), strip.text = element_text(size = 12)) } plot_experiment_results(plot_data)
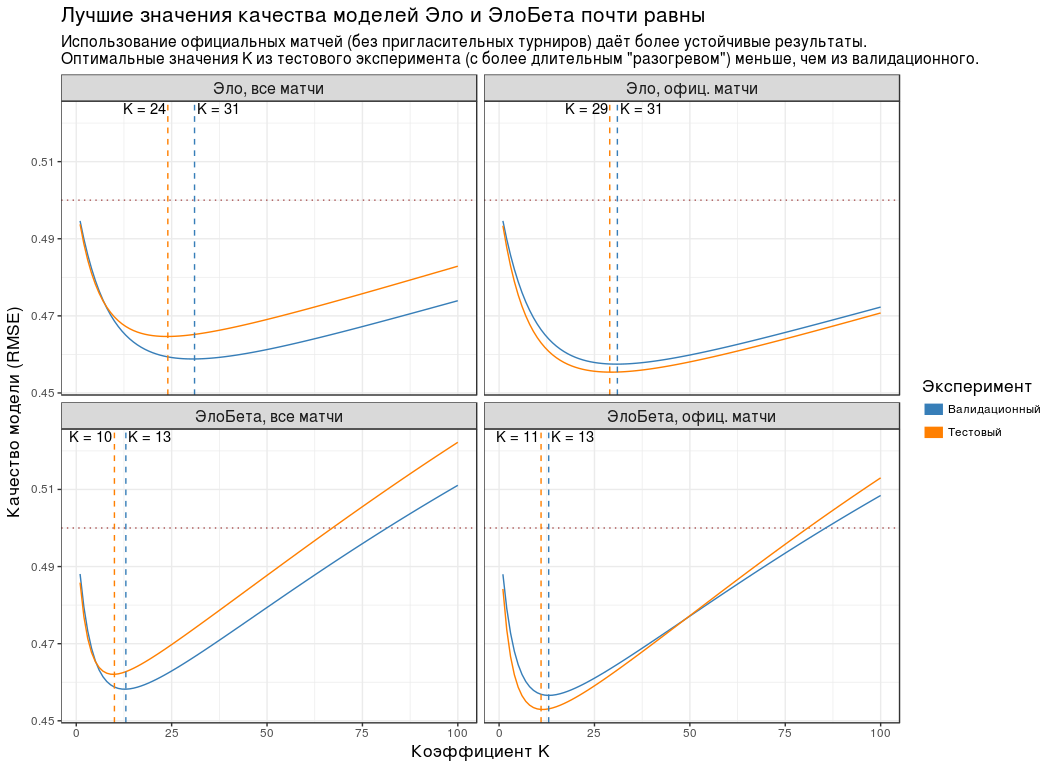
:
- , K , .
- ( "" "" ). , . - "Championship League": 3 .
- RMSE K . , RMSE K "" "". , " " .
- K ( "") , . "", .
- RMSE . 0.5. .
| K | RMSE |
|---|
| , | 24 | 0.465 |
| , . | 29 | 0.455 |
| , | 10 | 0.462 |
| , . | 11 | 0.453 |
Porque , K " " ( ) 5: 30, — 10.
, K=30 K=10 . , n , .
" " ( K=10 ) - .
-16 2017/18
-16 2017/18 # gather_to_longcr <- function(tbl) { bind_rows( tbl %>% select(-matches("2")) %>% rename_all(funs(gsub("1", "", .))), tbl %>% select(-matches("1")) %>% rename_all(funs(gsub("2", "", .))) ) %>% arrange(game) } # K best_k <- experiment_tbl %>% filter(testType == "test", ratingType == "elobeta", dataType == "off") %>% slice(which.min(goodness)) %>% pull(k) #!!! "" , .. !!! best_k <- round(best_k / 5) * 5 # elobeta_ratings <- rate_iterative( pro_matches_test_off, elobeta_fun_gen(best_k), initial_ratings = 0 ) %>% rename(ratingEloBeta = rating_iterative) %>% arrange(desc(ratingEloBeta)) %>% left_join( y = snooker_players %>% select(id, playerName = name), by = c(player = "id") ) %>% mutate(rankEloBeta = order(ratingEloBeta, decreasing = TRUE)) %>% select(player, playerName, ratingEloBeta, rankEloBeta) elobeta_top16 <- elobeta_ratings %>% filter(rankEloBeta <= 16) %>% mutate( rankChr = formatC(rankEloBeta, width = 2, format = "d", flag = "0"), ratingEloBeta = round(ratingEloBeta, 1) ) official_ratings <- tibble( player = c( 5, 1, 237, 17, 12, 16, 224, 30, 68, 154, 97, 39, 85, 2, 202, 1260 ), rankOff = c( 2, 3, 4, 1, 5, 7, 6, 13, 16, 10, 8, 9, 26, 17, 12, 23 ), ratingOff = c( 905750, 878750, 751525, 1315275, 660250, 543225, 590525, 324587, 303862, 356125, 453875, 416250, 180862, 291025, 332450, 215125 ) )
-16 2017/18 ( snooker.org):
| | | . | . | |
|---|
| Ronnie O'Sullivan | 1 | 128.8 | 2 | 905 750 | 1 |
| Mark J Williams | 2 | 123.4 | 3 | 878 750 | 1 |
| John Higgins | 3 | 112.5 | 4 4 | 751 525 | 1 |
| Mark Selby | 4 4 | 102.4 | 1 | 1 315 275 | -3 |
| Judd Trump | 5 5 | 92.2 | 5 5 | 660 250 | 0 0 |
| Barry Hawkins | 6 6 | 83.1 | 7 7 | 543 225 | 1 |
| Ding Junhui | 7 7 | 82.8 | 6 6 | 590 525 | -1 |
| Stuart Bingham | 8 | 74.3 | 13 | 324 587 | 5 5 |
| Ryan Day | 9 9 | 71.9 | 16 | 303 862 | 7 7 |
| Neil Robertson | 10 | 70.6 | 10 | 356 125 | 0 0 |
| Shaun Murphy | 11 | 70.1 | 8 | 453 875 | -3 |
| Kyren Wilson | 12 | 70.1 | 9 9 | 416 250 | -3 |
| Jack Lisowski | 13 | 68.8 | 26 | 180 862 | 13 |
| Stephen Maguire | 14 | 63.7 | 17 | 291 025 | 3 |
| Mark Allen | 15 | 63.7 | 12 | 332 450 | -3 |
| Yan Bingtao | 16 | 61.6 | 23 | 215 125 | 7 7 |
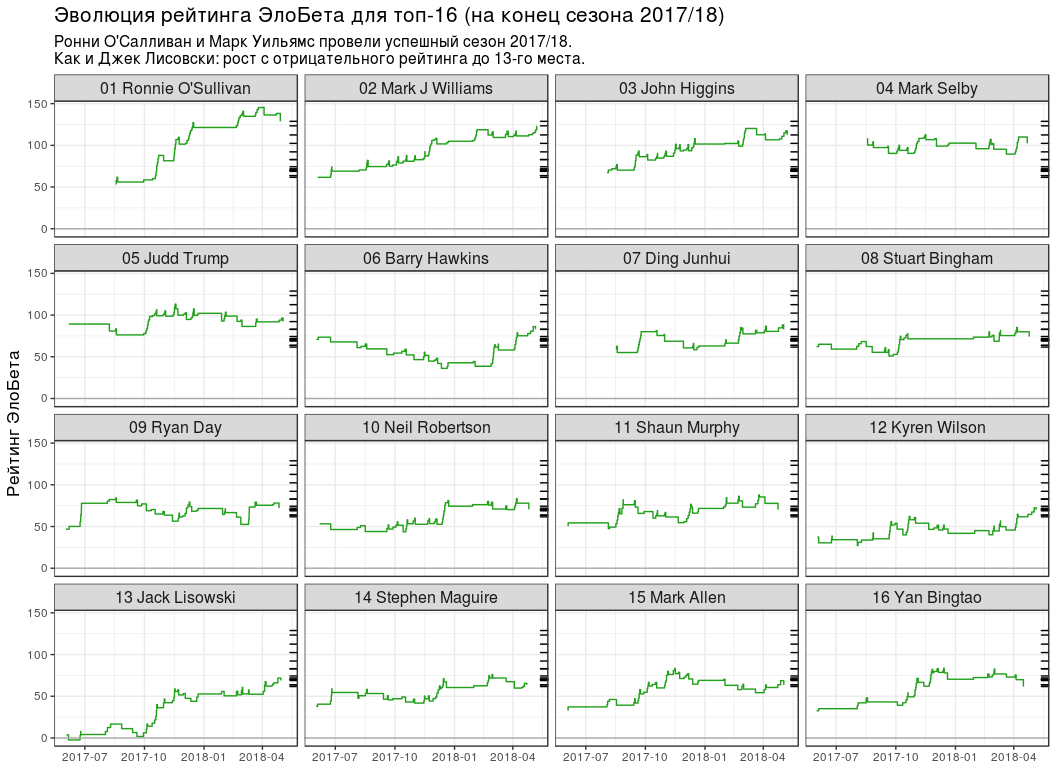
:
- №1 3 . , , ( ).
- "" ( 13 ), ( 7 ).
- 5 . , 6 - WPBSA. , - "" . : , — .
- .
- ( №11), (№14) (№15) -16. "" (№26), (№23) (№17).
. , №16 (Yan Bingtao) №1 (Ronnie O'Sullivan) 0.404. 4 0.299, " 10 " — 0.197 18 — 0.125. , .
# seasons_break <- ISOdatetime(2017, 5, 2, 0, 0, 0, tz = "UTC") # elobeta_history <- pro_matches_test_off %>% add_iterative_ratings(elobeta_fun_gen(best_k), initial_ratings = 0) %>% gather_to_longcr() %>% left_join(y = pro_matches_test_off %>% select(game, endDate), by = "game") # plot_all_elobeta_history <- function(history_tbl) { history_tbl %>% mutate(isTop16 = player %in% elobeta_top16$player) %>% ggplot(aes(endDate, ratingAfter, group = player)) + geom_step(data = . %>% filter(!isTop16), colour = "#C2DF9A") + geom_step(data = . %>% filter(isTop16), colour = "#22A01C") + geom_hline(yintercept = 0, colour = "#AAAAAA") + geom_vline( xintercept = seasons_break, linetype = "dotted", colour = "#E41A1C", size = 1 ) + geom_text( x = seasons_break, y = Inf, label = " 2016/17", colour = "#E41A1C", hjust = 1.05, vjust = 1.2 ) + scale_x_datetime(date_labels = "%Y-%m") + labs( x = NULL, y = " ", title = paste0( " -16 2016/17" ), subtitle = paste0( " ", " ." ) ) + theme(title = element_text(size = 13)) } plot_all_elobeta_history(elobeta_history)
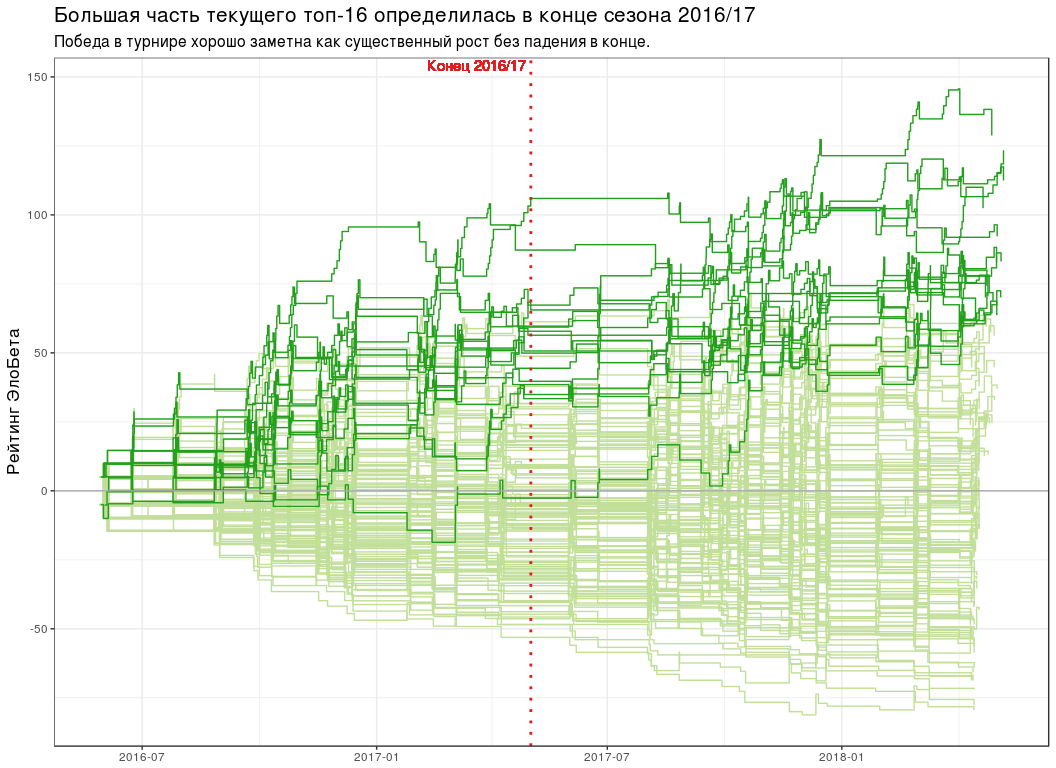
-16
-16 # top16_rating_evolution <- elobeta_history %>% # `inner_join` `elobeta_top16` inner_join(y = elobeta_top16 %>% select(-ratingEloBeta), by = "player") %>% # 2017/18 semi_join( y = pro_matches_test_off %>% filter(season == 2017), by = "game" ) %>% mutate(playerLabel = paste(rankChr, playerName)) # plot_top16_elobeta_history <- function(elobeta_history) { ggplot(elobeta_history) + geom_step(aes(endDate, ratingAfter, group = player), colour = "#22A01C") + geom_hline(yintercept = 0, colour = "#AAAAAA") + geom_rug( data = elobeta_top16, mapping = aes(y = ratingEloBeta), sides = "r" ) + facet_wrap(~ playerLabel, nrow = 4, ncol = 4) + scale_x_datetime(date_labels = "%Y-%m") + labs( x = NULL, y = " ", title = " -16 ( 2017/18)", subtitle = paste0( " ' 2017/18.\n", " : 13- ." ) ) + theme(title = element_text(size = 13), strip.text = element_text(size = 12)) } plot_top16_elobeta_history(top16_rating_evolution)
Conclusiones
- " " R :
pbeta(p, n, m) . - — "best of N " ( n ). .
- K=30 K=10 .
- :
sessionInfo() ## R version 3.4.4 (2018-03-15) ## Platform: x86_64-pc-linux-gnu (64-bit) ## Running under: Ubuntu 16.04.4 LTS ## ## Matrix products: default ## BLAS: /usr/lib/openblas-base/libblas.so.3 ## LAPACK: /usr/lib/libopenblasp-r0.2.18.so ## ## locale: ## [1] LC_CTYPE=ru_UA.UTF-8 LC_NUMERIC=C ## [3] LC_TIME=ru_UA.UTF-8 LC_COLLATE=ru_UA.UTF-8 ## [5] LC_MONETARY=ru_UA.UTF-8 LC_MESSAGES=ru_UA.UTF-8 ## [7] LC_PAPER=ru_UA.UTF-8 LC_NAME=C ## [9] LC_ADDRESS=C LC_TELEPHONE=C ## [11] LC_MEASUREMENT=ru_UA.UTF-8 LC_IDENTIFICATION=C ## ## attached base packages: ## [1] stats graphics grDevices utils datasets methods base ## ## other attached packages: ## [1] bindrcpp_0.2.2 comperank_0.1.0 comperes_0.2.0 ggplot2_2.2.1 ## [5] purrr_0.2.5 tidyr_0.8.1 dplyr_0.7.6 ## ## loaded via a namespace (and not attached): ## [1] Rcpp_0.12.17 knitr_1.20 bindr_0.1.1 magrittr_1.5 ## [5] munsell_0.5.0 tidyselect_0.2.4 colorspace_1.3-2 R6_2.2.2 ## [9] rlang_0.2.1 highr_0.7 plyr_1.8.4 stringr_1.3.1 ## [13] tools_3.4.4 grid_3.4.4 gtable_0.2.0 utf8_1.1.4 ## [17] cli_1.0.0 htmltools_0.3.6 lazyeval_0.2.1 yaml_2.1.19 ## [21] assertthat_0.2.0 rprojroot_1.3-2 digest_0.6.15 tibble_1.4.2 ## [25] crayon_1.3.4 glue_1.2.0 evaluate_0.10.1 rmarkdown_1.10 ## [29] labeling_0.3 stringi_1.2.3 compiler_3.4.4 pillar_1.2.3 ## [33] scales_0.5.0 backports_1.1.2 pkgconfig_2.0.1