Teoría de la felicidad. La ley de la cebra y la cola alienígena

Sigo familiarizando a los lectores de Habr con los capítulos de su libro "Teoría de la felicidad" con el subtítulo "Fundamentos matemáticos de las leyes de la maldad". Este libro de ciencia popular aún no se ha publicado, informa de manera muy informal acerca de cómo las matemáticas le permiten mirar el mundo y la vida de las personas con un nuevo grado de conciencia. Es para aquellos que están interesados ​​en la ciencia y para aquellos que están interesados ​​en la vida. Y dado que nuestra vida es compleja y, en general, impredecible, el énfasis en el libro se centra principalmente en la teoría de la probabilidad y las estadísticas matemáticas. Aquí no se prueban los teoremas y no se dan los fundamentos de la ciencia, de ninguna manera es un libro de texto, sino lo que se llama ciencia recreativa. Pero es precisamente un enfoque tan lúdico que nos permite desarrollar la intuición, alegrar las conferencias para los estudiantes con ejemplos vívidos y, por último, explicar a los no matemáticos y a nuestros hijos lo interesante que encontramos en nuestra ciencia seca.





Hablaremos sobre Fatum, terremotos, colas y procesos maravillosos: flujo de Poisson, caminata aleatoria y un poco sobre las cadenas de Markov.

Ley de cebra

Dicen que la vida es como una cebra: ya sea una franja blanca o una negra ... Y también sucede que otro se agrega a un problema, y ​​es tan difícil en la vida, ¡y luego el gato comenzó a dar a luz! ¡Es grueso, está vacío! Uno a uno! Pero lo más triste es que cuando una buena racha llega bien y en la vida, los malos pensamientos se arrastran: oh, no sería un vicio, oh, ¿no sería necesario pagar por la felicidad ... Una sensación familiar? En esta ocasión, se formula una de las leyes de la merfología: la segunda ley de Chisholm: " Cuando las cosas van bien, algo debería suceder en un futuro muy cercano ". Pero dado que Francis Chisholm, en su trabajo original, no proporciona un análisis detallado o evidencia de esta ley, trataremos de descubrir por nosotros mismos si existe alguna regularidad detrás de esto, o simplemente nos parece. Y si estas son las peculiaridades de las matemáticas, ¿es posible determinar la duración o frecuencia característica de las rayas en el cuerpo de nuestra cebra, y de qué depende?

En la vida, los eventos ocurren todo el tiempo. A veces no están conectados entre sí, a veces forman cadenas de relaciones de causa y efecto. Las discusiones sobre estas conexiones, cadenas y el camino predeterminado de la vida pueden llevarnos muy lejos, y hablaremos de ellas más adelante. Mientras tanto, intentemos, como siempre, sobrevivir con la menor cantidad de datos de entrada para el análisis de nuestra ley. Considere una secuencia de eventos no relacionados entre sí y vea qué puede obtener de ella.

Los eventos que de ninguna manera están relacionados y ocurren en el tiempo se describen aleatoriamente utilizando la conocida corriente de Poisson . Corresponde a muchos fenómenos aleatorios desde terremotos hasta la aparición de clientes en la tienda. La secuencia de eventos de Poisson se caracteriza por la intensidad o densidad de la secuencia , un parámetro que determina el número esperado de eventos por unidad de tiempo. Por ejemplo, al medir el tiempo en días, el valor del parámetro $$$\ lambda = 1/7$Habrá una cadena de eventos aleatorios, en promedio, que ocurren una vez por semana. Esto no significa que los eventos ocurrirán con una frecuencia de una vez por semana. Una secuencia de eventos puede no tener ninguna frecuencia asignada en absoluto. Es mejor imaginar una transmisión de Poisson con una intensidad de una vez por semana como esta: 52 semanas en un año, lo que significa que deberían ocurrir alrededor de 52 eventos por año (en promedio, durante muchos años). Si elegimos 52 fechas distribuidas de manera uniforme al azar en un año, entonces pueden considerarse como los momentos de la aparición de eventos de Poisson completamente independientes.


Un ejemplo de construcción de una corriente de Poisson con una intensidad de 1/7 (el tiempo se mide en días). Durante un intervalo de 365 días, 52 eventos no relacionados entre sí se dispersaron al azar.

Además, no se trata de ninguna periodicidad en estos eventos, cuando lo deseen, sucederá. Pero incluso en este lío, las estadísticas pueden mostrarnos ciertos patrones. Por ejemplo, la distribución de la duración de los períodos entre los eventos mostrados en la figura anterior no será uniforme en absoluto.


La densidad de la distribución de la duración de las brechas entre 52 eventos distribuidos aleatoriamente en el intervalo de 365 días.

La distribución de las duraciones de los huecos tiende a exponencial , se muestra mediante una línea continua. Para esta distribución, el máximo (modo) está en cero y el valor promedio es exactamente 7 días. Además, la desviación estándar también será igual a 7 días. La igualdad de la desviación estándar y el valor medio es una propiedad característica de la distribución exponencial. Como puede ver, estas características no garantizan en absoluto que pase una semana entre eventos, en promedio, sí, pero con mayor frecuencia, menos, además, se pueden observar intervalos bastante largos. Finalmente, la mediana muestra que la mitad de todos los intervalos tendrán una duración que no excederá los 5 días. La intensidad y la frecuencia no son lo mismo, ¡este es un punto muy importante!

Para ser justos, suponga que los eventos buenos y malos suceden igualmente probable, pero los eventos brillantes y significativos ocurren con mucha menos frecuencia que los pequeños e insignificantes. Que sea una vida normal en la que la coloración emocional de los eventos obedezca a la distribución normal (gaussiana). Así es como podría ser un año de destino sintético, como una serie de vicisitudes aleatorias de la vida absolutamente independientes:

Una serie de eventos de varios colores emocionales, formando una corriente de Poisson con una intensidad de 2/7 (2 eventos en 7 días).

Si bien no se observan bandas, en cambio hay algo de ruido. Cada evento transcurre sin dejar rastro, sin dejar nada en la memoria o el estado de ánimo. No sucede, démosle a nuestro héroe modelo un recuerdo, para empezar, ideal. Cada evento puede estar enterrado para siempre en su memoria y en su estado de ánimo, respectivamente, ya sea para mejorarlo o empeorarlo. Aquí hay una imagen que podemos obtener al observar el destino de nuestro héroe durante diez años.

Los eventos, que se funden en la memoria, forman el color emocional de la "vida sintética".

Bueno, bueno, ya vemos algún tipo de alternancia de humor, pero la imagen salió no muy alegre. Nuestro héroe, después de una serie de cambios de humor, cayó en una profunda depresión. Que mal. Probemos algunos destinos más. Todos ellos experimentan una serie de rayas claras y oscuras, pero durante mucho tiempo están empantanados en un anhelo desesperado o en una felicidad trascendente. Esto sucede, por supuesto, pero esto es claramente anormal.

Algunos ejemplos de "destinos sintéticos" de personas con recuerdos perfectos.

¡Relájate, amigo!

Describimos los destinos de nuestro modelo como un proceso muy notable, se llama caminata aleatoria unidimensional y tiene una serie de propiedades inusuales, entre las cuales hay una auto-similitud , es decir, la ausencia de cualquier escala temporal característica. Además, teniendo a su disposición un tiempo ilimitado, una caminata aleatoria puede llevarlo ilimitadamente lejos, y además, ¡ciertamente lo llevará a cualquier distancia predeterminada sobre el valor inicial! Por lo tanto, no importa cuán buenos sean sus asuntos, si están sujetos a vagar al azar, seguramente se deslizarán a cero y bajarán, ¡es solo cuestión de tiempo! Esta famosa e instructiva ley de la vida, recibió el nombre de maldición del jugador y su esencia se puede expresar con una simple máxima:

La mejor estrategia en el juego es tener un casino, de lo contrario, perderá.

No nos detendremos en este resultado, que ya es muy conocido, pero aún encontraremos esta propiedad de la caminata aleatoria unidimensional.

La memoria emocional perfecta no parece muy buena. ¡Nuestros héroes no olvidan nada y recuerdan cuidadosamente todo, incluso los eventos más antiguos! Su estado de ánimo en la vejez se ve afectado por el dolor de un juguete roto en la infancia o la alegría de un beso en la juventud. Además, todos los besos y juguetes posteriores son de igual importancia para ellos. Es necesario salvar a estos pobres tipos. Las emociones disminuyen con el tiempo, el dolor se vuelve aburrido, la alegría, por desgracia, también. Olvidar, en muchos sentidos, es como enfriar, difundir o ralentizar un movimiento en un fluido viscoso, por lo que es aconsejable simularlo de esta manera. Los procesos enumerados se denominan procesos de relajación . ¡Démosles a nuestros pobres compañeros la capacidad de relajarse!

El sistema relajante vuelve al estado de equilibrio, y cuanto más rápido, mayor es la desviación del equilibrio. Esta propiedad puede ser modelada por progresión geométrica o ley exponencial . Introducimos un nuevo parámetro en nuestro modelo: la tasa de olvido $$$\ mu$. Se puede expresar en el tiempo (en las lecturas de nuestro modelo), durante el cual el nivel de emoción disminuirá bastante. Por ejemplo, para $$$\ mu = 1/60$La huella emocional del evento disminuirá en un orden de magnitud en dos meses. ¡Y ahora la vida se ha convertido en un buen "rayado"!

La limitación de la memoria lleva al hecho de que una serie de eventos y sus huellas en la fusión de la memoria forman una serie de rayas de colores emocionales.

Cambiando el "grado de olvido", podemos obtener sujetos experimentales más o menos equilibrados emocionalmente. ¡Parece que hemos encontrado una fuente de cebra! Esto es, en primer lugar, caminatas aleatorias, propensas a extenderse en todas las direcciones, y en segundo lugar, curar el olvido, devolver el estado de ánimo a la normalidad. El resultado es un estado de ánimo serpenteante y ondulado.

Estudiemos las propiedades de las franjas mundiales "sintéticas" que hemos obtenido. Construimos un histograma que muestra la distribución de sus duraciones para una larga vida (o para muchas otras) con parámetros $$$\ lambda = 1/7, \ quad \ mu = 1/60$.

La distribución de la duración de los períodos de felicidad y dolor para una gran cantidad de destinos sintéticos. La línea vertical marca el valor promedio de 33.

Lo primero que llama la atención: la distribución máxima (moda) es cercana a cero, lo que significa que la mayoría de las veces los períodos de felicidad e infelicidad son muy cortos, sin embargo, también hay períodos que duran más de un año. En promedio, la duración de los períodos es de 33 días, con una desviación estándar de 36 días. Esta distribución es cercana a la exponencial (de hecho, está bien descrita por una distribución gamma más general con parámetros que la acercan a la exponencial). A su vez, la distribución exponencial de las longitudes de las bandas en la vida significa que los cambios de humor pueden considerarse como una corriente de Poisson, es decir, como una cadena de eventos aleatorios independientes que no tienen una frecuencia asignada, pero suceden con cierta intensidad conocida. Por ejemplo, en el ejemplo que hemos examinado, las rayas oscuras y claras cambian con una intensidad de una vez cada 33 días, pero al mismo tiempo, los períodos cortos se observan más en la vida: la mitad de ellos no son más de diez días.

En ausencia de "memoria" (para $$$\ mu = 0$), la distribución deja de disminuir exponencialmente y se convierte en exponencial.

La distribución de duraciones de meandros para una caminata aleatoria tiene la naturaleza de una distribución de potencia.

Los estadísticos dicen que tales distribuciones tienen una cola pesada , lo que hace que las desviaciones muy grandes del valor promedio sean bastante probables, las observamos en forma de largas "inmersiones" en ese otro estado de ánimo. La distribución obtenida por nosotros tiene una propiedad inusual y extraña: ni el valor promedio (valor medio), ni la desviación estándar, ni la mediana se definen para ello. El hecho es que todas estas características se calculan en función del área bajo la curva de densidad de distribución, y es infinita. A este respecto, se puede escuchar que el valor promedio en este caso es infinito, pero esto no es así. Vea lo que sucede cuando intenta calcular el valor promedio de la duración del meandro de una caminata aleatoria:

Tratando de calcular el valor promedio para una secuencia de períodos de períodos entre cambios de humor en ausencia de memoria. Los valores extremos emergentes de la cola pesada de la distribución conducen al hecho de que el valor del promedio no converge a ningún valor.

Los saltos enormes que se originan en la cola pesada derriban continuamente el valor promedio y la secuencia del promedio no converge a ningún límite. El valor medio no es infinito en absoluto, solo la integral no converge a ningún número y es imposible hablar de ningún valor específico. La imposibilidad de calcular el valor medio de la duración del meandro es lo que refleja la propiedad de auto-similitud de las caminatas aleatorias, es decir, la ausencia de una escala de tiempo adecuada.

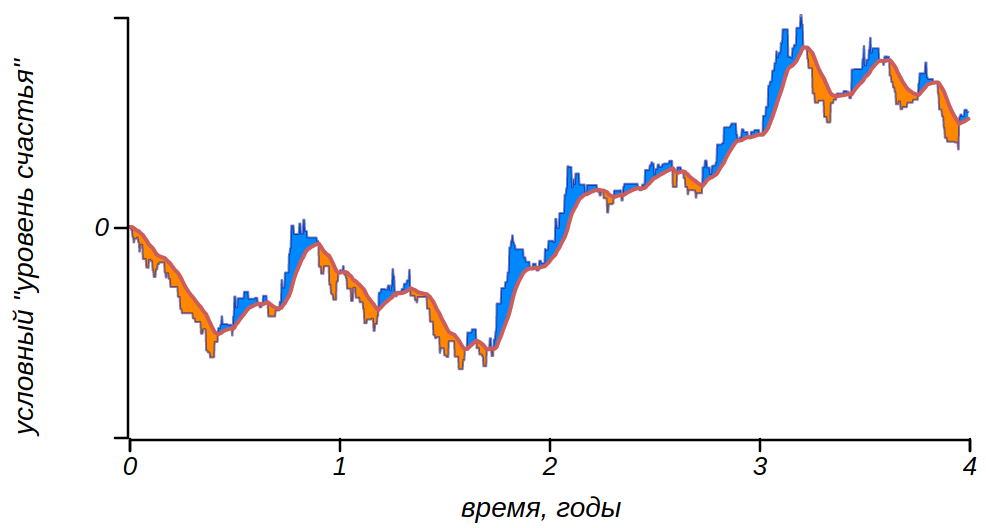
Simulamos la adaptabilidad a la agitación cotidiana con la ayuda de la relajación o la atenuación de los arrebatos emocionales. Este proceso puede interpretarse de otra manera, como la adaptabilidad de una persona a las circunstancias de la vida. Al procesar señales o secuencias ruidosas, el método de promedio móvil se usa a menudo para suavizar y seleccionar una señal útil, considerando en cada momento no la señal en sí, sino el valor promedio de la señal durante un cierto período de tiempo. Por lo tanto, es posible deshacerse del ruido y tener una idea de las tendencias a largo plazo de la señal. Aplicando tal promedio a la agitación cotidiana, podemos simular la adaptabilidad humana. Y durante las guerras, la gente se enamora y encuentra motivos para la alegría, así como la vida de los ociosos ricos no está despejada. La norma está cambiando, de lo cual el estado de ánimo se desvía en una dirección u otra. Teniendo en cuenta la diferencia entre una secuencia de emociones y una línea de fondo suave, obtenemos la misma imagen, rayas, que el modelo anterior nos dio, con las mismas características estadísticas. Esto no es sorprendente, porque conceptualmente prácticamente no difieren, describiendo un sistema con relajación.

El estado de ánimo errante y cambiante se puede obtener simulando el promedio móvil de la adaptabilidad de una persona a las circunstancias.

Conectado por una cadena

En los modelos considerados, recibimos una secuencia de Poisson de cambios de humor, generando eventos con una secuencia de Poisson. Uno puede ver algunos aparejos en esto: el proceso aleatorio de Poisson resultó ser "cosido" en el modelo. ¿Cuán universal es nuestro resultado? ¿Es posible obtenerlo de alguna manera diferente?

La experiencia mundana es algo poco formalizado y se puede adaptar a varias herramientas matemáticas, lo que permite no solo simplificar los supuestos, sino también la especulación. En ciencia, este enfoque es inaceptable, pero en nuestro viaje a través de los métodos de la teoría de los procesos aleatorios, podemos permitirnos jugar con ellos para conocerlos mejor.

Al observar la dinámica del estado de ánimo y la percepción del mundo, se puede ver que es la naturaleza humana "mantenerse" en un determinado estado de ánimo. Si las cosas van bien en general, entonces las malas noticias pueden recibirse con optimismo. Y, por el contrario, el estado de ánimo melancólico, una vez ingerido por una persona, puede estropear incluso las noticias alegres. Desde un punto de vista matemático, esto significa que la probabilidad de permanecer en el estado de ánimo actual es mayor que la probabilidad de cambiarlo. Este comportamiento se puede describir utilizando un proceso aleatorio llamado cadena de Markov . En el caso general, una cadena de Markov puede representarse como un conjunto fijo de estados con transiciones entre ellos, y las transiciones de estado a estado tienen una probabilidad diferente pero conocida. Es conveniente representar tales cadenas en forma de gráficos ponderados, por ejemplo, una cadena simétrica elemental de Markov que describe la dinámica del estado de ánimo se puede representar de esta manera:


Cadena de Markov con dos estados ("alegre" y "triste"). Las flechas indican las transiciones y las probabilidades de estas transiciones. En nuestro caso simétrico, la probabilidad de permanecer en un estado de ánimo existente excede la probabilidad de su cambio, pero no depende del estado de ánimo en sí.

Nuestra cadena es capaz de generar secuencias de estados y, por supuesto, aparecerán bandas de cebras mundanas.



Lo más interesante es averiguar qué distribución estará sujeta a la duración de estas bandas. Para nuestro modelo más que simple, la respuesta puede ser exacta: esta es una distribución geométrica que describe la probabilidad de observar un número dado de pruebas de un experimento aleatorio antes de observar el primer "éxito".

Un histograma para la duración de períodos del mismo estado de ánimo en la secuencia generada por la cadena simétrica de Markov y la función de probabilidad de la distribución geométrica con un parámetro igual a la probabilidad de transición entre estados. La secuencia es de diez años.

Una distribución geométrica es un análogo discreto de una distribución exponencial, en el sentido de que los valores redondeados de una variable aleatoria distribuida exponencialmente la obedecen. Existe una relación entre el parámetro de distribución geométrica y la intensidad de la distribución exponencial correspondiente. , , $$$\lambda = -ln(0.75) \approx 2/7$.

, «» «», «» . , , , . - .


, . .

Las cadenas de Markov son una herramienta poderosa para analizar procesos aleatorios en los que se encuentra un determinado algoritmo o escenario. Nos dan una mirada peculiar a los procesos que se consideran cíclicos. Por ejemplo, la conocida máxima: "la historia de la humanidad camina en círculo" a menudo se interpreta como el hecho de que hay ciertos ciclos o incluso periodicidades en la historia. Uno tiene que escuchar, por ejemplo, que el comienzo del siglo promete agitaciones y guerras. A riesgo de entrar en mi propio tema, me atreveré a suponer que, de hecho, tiene sentido hablar no de ciclos literales, sino de escenarios más o menos estables: cadenas regulares que pueden describirse mediante una cadena de Markov. Entre las cadenas de Markov hay una clase de cadenas cíclicas que, de hecho, pueden crear secuencias repetitivas.Sin embargo, no existe una verdadera periodicidad determinista en su comportamiento. Ocurriendo al azar en diferentes períodos históricos y en diferentes contextos, tales ciclos son similares entre sí y pueden crear una sensación de "deja vu" histórico. Es útil estudiarlos y describirlos, pero quizás no debas esperar un plan de calendario estricto.

Sobre esto cerramos el tema de la cebra. ¿Qué conclusiones se pueden sacar de nuestra frívola investigación? Una serie de rayas claras y oscuras en la vida no es una ilusión, realmente lo son. Pero no hay patrones particulares en ellos. Muy a menudo son cortos, pero también son prolongados. Todo depende de la facilidad de carácter y la capacidad de dejar atrás el pasado. Además, si los eventos en la vida rara vez suceden, la vida se convertirá en una serie gris de recuerdos que desaparecerán en el pasado. Por lo tanto, nos interesa recordar lo que se ha vivido y está en nuestro poder asegurar que la vida no se convierta en una caminata aleatoria. Podemos hacer que los buenos eventos se hagan más grandes y sucedan con más frecuencia, incluso si son insignificantes. Un viaje de esquí, la sincera sonrisa de un transeúnte, una entrada para un concierto, una taza de chocolate caliente en un día frío,Todo esto ayudará a crear una tendencia positiva y extender la racha brillante en la vida. Es cierto que el valor promedio seguirá la tendencia, por lo que los eventos tristes inevitables necesariamente cambiarán el estado de ánimo. Pero no culpes a tu felicidad por esto. Esto no es una retribución para él, y no el mal de ojo. Esta propiedad de los sistemas relajantes es una tendencia a las oscilaciones durante la acción externa estocástica.

() , . , , , , : , . - , , .

, , - 2018 : « 7.7, 7-9 . -, 52.3%.» ¿Qué significa esto? ? ? ? . : , 500 52 ( ). , . , - , : , 60 / 60 . , , , , , 500 52 . , , , -. , , , .

Observe cómo cambia el nivel de actividad sísmica de la región de Kamchatka a diferentes escalas de tiempo (imagen tomada del sitio del Monitor de Actividad Sísmica de la rama de Kamchatka de la Encuesta Geofísica Unificada de la Academia de Ciencias de Rusia)


El nivel inferior de actividad se reemplaza por uno mayor, la actividad "respira", pero no periódicamente, sino como el mismo vagabundeo aleatorio con relajación.

Pero los terremotos, sin embargo, son fenómenos desagradables y no permiten que sucedan por más tiempo. Hay cosas que espera con gran impaciencia, como un autobús. Al llegar a la parada de autobús, por supuesto, deseamos tomar instantáneamente la ruta deseada de autobús o tranvía, pero lo más probable es que esto falle. Luego, si hay un horario claro en este lugar, lo miramos, luego el reloj y luego nos sumergimos en un libro o teléfono. Pero a menudo, en el medio de la ruta, en lugar del horario, se indica el intervalo de tráfico, por ejemplo, 15 minutos. Esto significa que ya estamos lejos de la estación de autobuses con la que los autobuses salen exactamente a tiempo, y se está acumulando algún error, lo que hace que la llegada del autobús sea aleatoria. Bueno, 15, entonces 15, esperemos. Y aquí debe tener en cuenta que, en promedio, debe esperar exactamente 15 minutos, independientemente de cuándo venga.Ahora, si vinieran autobusescon una frecuencia de 15 minutos, el tiempo de espera promedio sería la mitad del período: 7.5 minutos, ¡pero con intensidad no funcionará! En ausencia de condiciones adicionales, el movimiento del transporte está modelado por una corriente de Poisson, lo que significa que el tiempo de espera para el autobús obedecerá la ley exponencial con la misma intensidad. Y la expectativa matemática de una cantidad distribuida exponencial con intensidad$$$\lambda$ es igual $$$1/\lambda$, . — , - . , , .

. , : , , : — . , 17 , , , , . , , alarga efectivamente el tiempo de espera observado.


Curiosamente, la curva de Lorentz para la distribución exponencial es la misma para cualquier intensidad. Por lo tanto, la afirmación es cierta para todos los procesos de Poisson: la mitad del tiempo total de observación ocurre en el 20% de los casos cuando este próximo evento se retrasa. El coeficiente de Gini para la distribución exponencial es exactamente 1/2.

Turno alienígena

Pienso en las leyes de la mezquindad, haciendo cola en el aeropuerto para el registro de pasajeros y equipaje. La cola es larga, las personas son diferentes y notables con todas sus bolsas, niños o jaulas. Escucho un gruñido desde atrás: “Como siempre, nuestro turno es lento. Mira, mira, ese bigotudo con gorra estaba a la altura de nosotros, y ahora por allá ... ¡Esa es la ley de la maldad! ¡Mi turno siempre es lento! Esta ley se llama la observación de Ettore:

« .»

, . , , . , . , , , , . .

:

Mover dos colas adyacentes a medida que Poisson procesa con igual intensidad.

A su vez, la diferencia entre dos procesos de Poisson idénticos, es decir, si la observa una persona aburrida en la cola, es una especie de caminata aleatoria. Y si es así, entonces estamos listos para sacar algunas conclusiones. Primero: la distancia entre personas que permanecen simultáneamente en las mismas colas aumentará o disminuirá, y se formarán meandros característicos con una duración siempre cambiante. La segunda conclusión: debido a la auto-similitud de las caminatas aleatorias para ráfagas cortas y largas, los meandros tendrán una duración comparable al tiempo en la cola, lo que significa que serán notables, y los meandros serán motivo de descontento. La tercera conclusión: no se sabe de antemano qué cola irá más rápido, ya que una caminata aleatoria igualmente irá hacia arriba y hacia abajo. Y, finalmente, la cuarta conclusión: las colas se mueven de forma independiente, de vez en cuando y se ponen al día entre sí, en promedio, se mueven de la misma manera, y la diferencia esperada entre ellas tiende a cero, pero la extensión alrededor del promedio aumenta con el tiempo (en el caso descrito por nosotros, el valor el retraso de una cola de otra está sujeto a la distribución de Skellam ). Resulta que, o adivinó con una línea rápida o no, ¡no hay cosas malas del villano del destino!

Pero las leyes de la maldad no se llamarían leyes si no reclamaran la universalidad. Si no tenemos la suerte de estar en la línea rezagada, ¡pasaremos más tiempo en ella y tendremos más oportunidades de quejarnos sobre el destino! Y ahora, atención, buenas noticias: en cualquier intervalo de tiempo seleccionado, aquellos que tienen la suerte de entrar en la cola rápida más que las personas desafortunadas, ¡porque la cola rápida puede perder a más personas! Pero, por desgracia, esto no consolará a nadie que esté atrapado en la cola.

---

El texto enviado aún no se ha publicado, lo que significa que puede cambiar. Espero que los comentarios y comentarios de los lectores de Habr lo ayuden a cambiar para mejor.