Un capítulo del libro de Alexander Voloshinov "Matemáticas y Arte" (Moscú: Ilustración, 1992)
El venerable Pitágoras rechazó la evaluación de la música basada en la evidencia de los sentimientos. Argumentó que sus virtudes deberían ser percibidas por la mente y, por lo tanto, juzgó la música no de oído, sino sobre la base de la armonía matemática y consideró que era suficiente limitar el estudio de la música a una octava.PlutarcoEstrictamente hablando, estamos hablando del sistema pitagórico. ¿Qué es gamma y escala en la música?
Gamma , o escala , es una secuencia de sonidos (pasos) de algún sistema musical (traste), ubicado, comenzando desde el sonido principal (tono principal), en orden ascendente o descendente. El nombre "gamma" proviene de la letra griega Gγ (gamma), que en la Edad Media denotaba el tono extremadamente bajo de la escala, y luego toda la escala.
La característica más importante de un sonido musical es su tono , que es un reflejo en la conciencia de la frecuencia de oscilación de un cuerpo que suena, como una cuerda. Cuanto mayor es la frecuencia de oscilación de la cuerda, más alto se nos aparece el sonido.
Cada sonido individual no forma un sistema musical y, si no es demasiado fuerte, no nos causa mucha reacción. Sin embargo, la combinación de dos sonidos ya en otros casos resulta agradable y armoniosa, y en otros, por el contrario, "corta" el oído. Una combinación acordada de dos sonidos se llama consonancia , una combinación inconsistente se llama disonancia . Está claro que la consonancia o disonancia de dos tonos está determinada por la distancia de altitud entre estos tonos o el intervalo.
El intervalo entre dos tonos es el número de serie del tono del tono superior en relación con el inferior en esta escala, y el coeficiente de intervalo I 21 de dos tonos es la relación entre la frecuencia del tono superior y la frecuencia del inferior * :
(6.1)
* ( En la teoría de la música, los conceptos de intervalo y coeficiente de intervalo no se distinguen estrictamente. Siguiendo la tradición, a menudo nos referimos al coeficiente de intervalo por brevedad como un intervalo ) .
Consideremos ahora un cierto conjunto de sonidos presionando, por ejemplo, varias teclas en un piano. Lo más probable es que obtengamos un conjunto incoherente de sonidos, como dicen, ni el almacén ni el traste. En otros casos, los sonidos parecen encajar, se llevan bien entre ellos, pero su combinación parecerá irregular, inacabada. Me gustaría continuar con esta secuencia hasta una cierta nota, que en este sistema de sonidos parece ser la más estable, básica y llamada tónica . Entonces, los sonidos en un sistema musical están interconectados por ciertas dependencias, algunos de ellos son inestables y gravitan a otros, estables .
Pero no solo el tónico y la combinación de sonidos estables e inestables determinan la naturaleza del sistema musical. Es fácil asegurarse presionando ocho teclas blancas seguidas de nota a (escala a mayor natural ) y de nota la ( natural menor a menor ) que estas escalas suenan de manera diferente: la primera - mayor - suena alegre y ligera, y la segunda - menor - triste y nublado * . Por lo tanto, hay otra característica del sistema de sonido: el estado de ánimo: mayor o menor. Por lo tanto, llegamos a uno de los conceptos más complejos en la teoría de la música: el concepto de traste.
* (La naturaleza del sonido del traste, por supuesto, no se define tan cruda e inequívocamente. Esta pregunta es muy delicada, y hablaremos de ello al final del capítulo ) .
Un traste es una interacción de sonidos musicales que es agradable a la audición, determinada por la dependencia de los sonidos inestables de los sonidos estables y, en primer lugar, del sonido estable principal - tónico, y que tiene un cierto carácter de sonido - inclinación. La historia de la cultura musical conoce muchos modos característicos de diferentes pueblos y diferentes épocas. Los antiguos griegos sabían sobre una docena de trastes, y los trastes de algunos países del este y la India son extremadamente complejos, peculiares e inusuales para la audiencia europea. Los modos modernos más comunes consisten en siete pasos principales, cada uno de los cuales puede aumentar o disminuir, lo que proporciona cinco sonidos adicionales más. Por lo tanto, el traste gamma diatónico (7 pasos) se convierte en cromático (12 sonidos). El primer paso del traste es el tónico. Las leyes de la estructura del traste son una ciencia completa, la piedra angular de la musicología, y muchos científicos y compositores han dedicado toda su vida al estudio de estas leyes.
Nos interesarán principalmente las leyes matemáticas que describen la estructura del traste, es decir, el sistema musical. El sistema musical es la expresión matemática de un cierto sistema de relaciones de tono. Además del interés puramente teórico, el sistema encuentra aplicación en la afinación de instrumentos musicales con un tono fijo de sonidos, como un piano u órgano.
En conclusión, notamos que nuestros experimentos al presionar las teclas en el piano pueden terminar con el fenómeno más raro y agradable, cuando el sistema de sonido tomado no solo pertenecerá a un traste, sino que también será significativo. Una serie secuencial de sonidos artísticamente significativos de diferentes alturas se llama melodía . Esto es justo lo que nos encanta tararear dependiendo de nuestro estado de ánimo: alegre, triste, alegre ...
Después de una corta excursión a la musicología teórica, podemos regresar a las orillas del soleado Hellas durante el tiempo de los sabios Pitágoras. Intentaremos restaurar el razonamiento de Pitágoras y sus estudiantes cuando construyan el sistema pitagórico, porque fue este sistema el que determinó durante milenios, si no para siempre, el desarrollo completo de la cultura musical, no solo europea, sino también oriental. El mismo Pitágoras no dejó ninguna obra escrita, y el legado de los pitagóricos parece ser una pila de ruinas sin esperanza, es decir, una colección de fragmentos que sobrevivieron accidentalmente y citas posteriores. Sin lugar a dudas, estas ruinas son hermosas y aún sorprenden a la imaginación, como las ruinas del famoso Partenón, pero gran parte de estos fragmentos se pierden por completo y a menudo solo se puede adivinar el conjunto. Y aun así ...
Monochord - single-string - fue uno de los primeros instrumentos musicales de los antiguos griegos. Era una caja larga necesaria para amplificar el sonido sobre el cual se tiraba la cuerda. Desde abajo, la cuerda fue jalada por un soporte móvil para dividirla en dos partes que suenan por separado. En una caja de madera debajo de la cuerda había una escala de divisiones, lo que hizo posible determinar con precisión qué parte de la cuerda suena. Por supuesto, como instrumento musical, el monocordio nos parecerá demasiado primitivo, pero fue un excelente instrumento físico y una herramienta de enseñanza sobre la cual los antiguos contempladores comprendieron la sabiduría de la alfabetización musical.
Los antiguos afirmaron que Pitágoras ya conocía las leyes de vibración de la cuerda monocorda y la construcción de consonantes musicales (consonantes), sin embargo, encontramos un registro de estas leyes de los arquitectos pitagóricos de Tarento (428-365 aC), que vivieron un siglo y medio más tarde que Pitágoras. . El arquitecto fue sin duda el representante más destacado de la escuela pitagórica, un amigo del filósofo Platón y un maestro del matemático Eudoxo (c. 408 - c. 355 a. C.), un estadista y comandante. La versatilidad de Architus es sorprendente: resolvió el famoso problema de doblar el cubo, fue merecidamente considerado el mayor teórico de la música pitagórica, el primero en racionalizar la mecánica basada en las matemáticas y reducir los movimientos de los mecanismos a dibujos geométricos, trabajar en un modelo de madera de una paloma voladora. Según Van der Waerden, Arch es el autor del libro VIII "Los comienzos" de Euclides, que expone la teoría aritmética de las proporciones. Como estadista, Archit era extremadamente respetado: fue elegido estratega siete años seguidos * , aunque por ley, los estrategas fueron elegidos solo por un año. A través de hábiles maniobras diplomáticas, el Archit rescató a Platón del cautiverio y de ese modo salvó la vida del gran filósofo. "Arquitectos gloriosos, tierras y mares, y calculadora de arena ..." - escribió Horace.
* ( Estratega: en las antiguas ciudades-estado griegas, un líder militar dotado de poderes militares y políticos Shi-ki ) .
Las "Leyes de Pythagoras-Archite", en las que se basó toda la teoría de la música pitagórica, pueden formularse de la siguiente manera:
1- El tono (frecuencia de oscilación f) de la cadena de sonido es inversamente proporcional a su longitud l:
(6.2)
aquí a es el coeficiente de proporcionalidad, dependiendo de las propiedades físicas de la cuerda (grosor, material, etc.).
2. Dos cuerdas sonoras dan consonancia solo cuando sus longitudes se denominan enteros que forman el número triangular 10 = 1 + 2 + 3 + 4, es decir, como 1: 2, 2: 3, 3: 4.
Estos intervalos son "consonantes perfectas", y sus coeficientes de intervalo se les dieron más tarde los nombres latinos * :
* ( Los nombres de los intervalos en la música son números latinos, que indican el número de serie de la escala de la escala que compone el intervalo con la etapa inicial: octava - octava, quinta - quinta, cuarta - cuarta, etc. )
octava
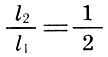
quint
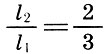
cuarto de galón
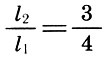
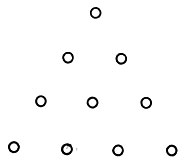
Triangular numero 10
También se observó que la fusión más completa de tonos está dada por una octava (2/1), seguida de una quint (3/2) y un cuarto (4/3), es decir, cuanto menor es el número n en relación con la forma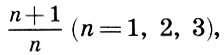 
cuanto más consonante es el intervalo.
"La segunda ley de Pitágoras - Arquitecto" y ahora parece sorprendente. ¡Qué podemos decir sobre los pitagóricos, a quienes simplemente cautivó! Aquí encontraron la confirmación de toda su filosofía: los enteros, además, los números tetraktis lo gobiernan todo, ¡incluso la música! Los pitagóricos no se hicieron esperar mucho y extendieron la ley de las relaciones musicales siempre que fue posible, incluida la estructura del universo.
Entonces, si tomamos el segmento l igual a 1/12 de la longitud de la cadena de monocordio l 1 como el precio de dividir la escala de monocordio, entonces, junto con la cadena de monocordio completa de longitud l 1 = 12l, sus partes de longitud l 2 = 6l serán consonantes: el sonido es una octava más alta (l 2 / l 1 = l / 2), l 3 = 9l - suena un poco más alto (l 3 / l 1 = 2/3) y l 4 = 8l - suena un cuarto más alto (l 4 / l 1 = 3/4 ) Esta consonancia y sus números definitorios 6, 8, 9, 12 se llamaron tétrada (cuatro). Los pitagóricos creían que la tétrada era "esa escala según la cual cantan las sirenas". Al afinar la antigua lira, que se convirtió en el símbolo de la música, sus cuatro cuerdas se afinaban necesariamente según la regla de la tétrada, y la afinación de las cuerdas restantes dependía del traste en el que tocarla.
Pero para el pensador antiguo no fue suficiente establecer los valores numéricos de las cantidades estudiadas. El ojo y la mente pitagóricos están acostumbrados no solo a medir, sino también a medir, es decir, a revelar las conexiones internas entre los sujetos estudiados, en otras palabras, a establecer relaciones proporcionales. El arquitecto era un verdadero pitagórico, y estableció relaciones proporcionales entre la principal consonancia perfecta: una octava, una quinta y una cuarta. Esta decisión fue obtenida por los arquitectos en relación con el deseo de dividir la octava en intervalos armoniosos. Probablemente, Arch se basó en el supuesto intuitivamente obvio de que, junto con los tonos f 1 y f 2 = 2f 1 , dando la consonancia principal - una octava, la consonancia y su media aritmética f 3 = (f 1 + f 2 ) / 2 deberían dar. Pero entonces la longitud de la cadena l 3 se expresará en términos de longitudes de cadena l 1 y l 2 de acuerdo con (6.2) de la siguiente manera:
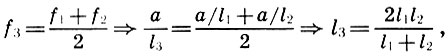
es decir, l 3 es la media armónica l 1 y l 2 (ver 5.1). Lo contrario también es fácil de detectar: la media armónica para las frecuencias f 1 y f 2 entra en la media aritmética para las longitudes l 1 y l 2 :
Recordando eso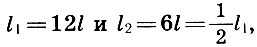 
Junto con los arquitectos, llegamos a una conclusión importante:
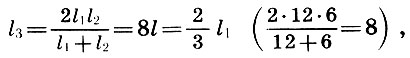
(6.3)
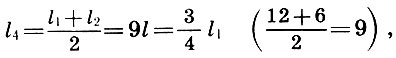
(6.4)
es decir, el quinto es la media armónica de las longitudes de las cuerdas del tono fundamental l 1 y las octavas l 2 , y el cuarto es el promedio aritmético de l 1 y l 2 .
Pero el producto de la media aritmética y la media armónica es igual al producto de los números originales:
(6.5)
de ahí, dividiendo ambas partes por l 1 2 , obtenemos la segunda conclusión importante:
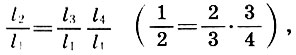
(6.6)
o
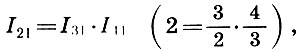
es decir, una octava es el producto de un quinto a un cuarto.
Dividiendo (6.5) entre l 1 l 3 , Archite obtiene la tercera de las proporciones principales: geométrica:
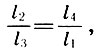
(6.7)
que se llamaba "musical": una octava se relaciona con un quint tanto como un cuarto con un tono fundamental .
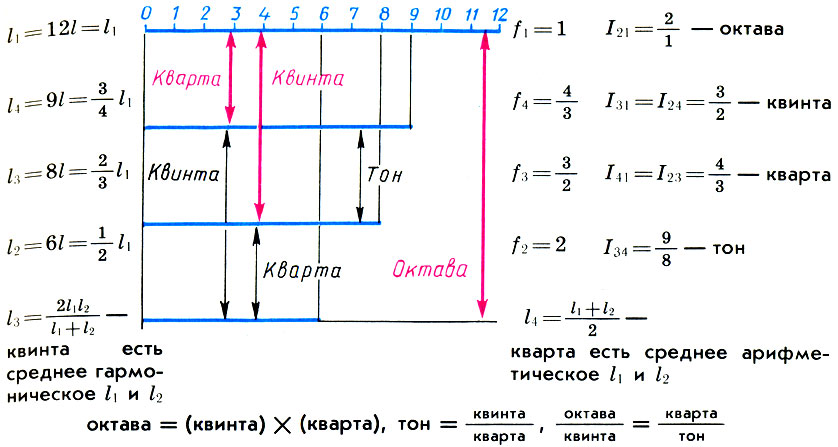
División de una cuerda monocordial (l 1 ) en partes que forman consonantes perfectas con ella: una octava (l 2 ), una quinta (l 3 ) y un cuarto (l 4 ) y las relaciones entre ellas. Los intervalos que forma una cadena completa de monocorda con sus partes se muestran con flechas rojas.
Es fácil obtener dos relaciones más:
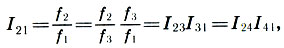
(6.8)
es decir, la octava se divide en dos intervalos de consonantes desiguales: el quinto y el cuarto . Un intervalo que extiende este intervalo a una octava se llama inversión . Por lo tanto, el quint es el inverso del cuarto y viceversa.
Finalmente, encontramos el coeficiente de intervalo entre las cuerdas del quinte l 3 y el cuarto l 4 , que junto con su intervalo se llama tono (no confunda el intervalo de tono y el sonido de tono de una altura dada):
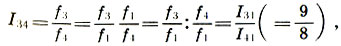
(6,9)
es decir, el intervalo de tono es igual a la relación del quinto al cuarto .
Tenga en cuenta que, en contraste con la distancia habitual en la línea recta r 21 = x 2 - x 1 definida como la diferencia entre las coordenadas del final y el principio, el coeficiente de intervalo - la distancia de altura - se define como la relación de los tonos que lo componen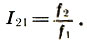 
Luego, tres tonos f 1 <f 2 <f 3 ubicados a distancias iguales r y formando una progresión aritmética x 1 , x 2 = x 1 + r, x 3 = x 1 + 2r. Por lo tanto, los coeficientes de intervalo se suman y restan "geométricamente", y los intervalos mismos - "aritméticamente", como distancias habituales, a saber:
la suma de dos intervalos es igual al producto de sus coeficientes de intervalo:
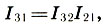
(6.10)
la diferencia de dos intervalos es igual al cociente de sus coeficientes de intervalo:
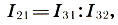
(6.11)
dividir el intervalo en n partes iguales significa extraer una raíz de grado n de su coeficiente de intervalo:
(6.12)
etc.
Para pasar de coeficientes de intervalo a intervalos de distancia, es suficiente introducir el intervalo logarítmico L = log a I y la frecuencia logarítmica F = log a f. Luego, el logaritmo de definición (6.1) y las igualdades (6.10) - (6.12) obtenemos la definición habitual y las reglas de acción con distancias:
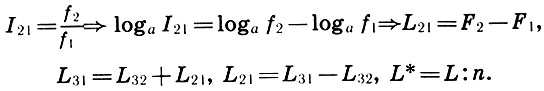
(6.13)
La solución del problema de división de octava provocó que Archit inmediatamente dos evidencias de irracionalidad 
. De hecho, si tratamos de dividir la octava en dos intervalos iguales I, entonces, poniendo (6.8) I 23 = I 31 = I, tenemos
Pero con esta proporción de longitudes de cuerda, se escucha una clara disonancia. Como la consonancia está determinada por la razón de los enteros de la forma (n + 1): 2, la idea sugiere que el número no puede expresarse por la razón de dos enteros, es decir, es irracional.
La segunda prueba de irracionalidad. menos musical, pero más matemático. Para encontrar la raíz cuadrada de un número que no es un cuadrado completo, Archit lo descompone en dos factores desiguales (2 = 1 * 2), luego forma la media aritmética 3/2 y la media armónica 4/3 a partir de estos factores y compone una proporción musical a partir de estos números ( 6.7):
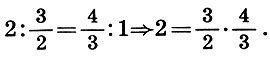
El producto de los términos medios de esta proporción es igual a un número dado 2, y su diferencia 
menor que la diferencia de la aproximación zeroth 2 - 1 = 1. Por lo tanto, 
puede considerarse como valores aproximados .
(3/2 con exceso, 4/3 con deficiencia].
Habiendo realizado el mismo procedimiento sobre las primeras aproximaciones, obtenemos las segundas aproximaciones:
por otra parte
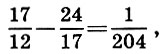
y luego las terceras aproximaciones:
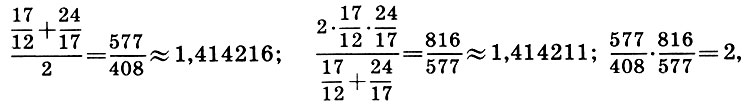
por otra parte
1.414216-1.414211 = 0.000005.
Dado que este procedimiento puede repetirse indefinidamente, está claro que el número irracional En el camino, estamos convencidos de la exactitud de la idea de Pitágoras de que cuanto más grandes son los enteros en la relación, más exactamente expresan el número irracional (ver pág. 96). Finalmente, recordando ese significado es igual a 1.414213 ..., vemos que el método "musical" de Archit converge muy rápidamente al valor exacto ¡y ya la tercera aproximación da cinco decimales correctos!
Pero volvamos a nuestros intervalos. Entonces, la octava se divide en dos consonantes desiguales de la quinta y cuarta, y la quinta, por la cuarta y la disonancia. El intervalo de tono se tomó como el intervalo entre los sonidos vecinos (pasos) en altura al construir la escala de Pitágoras. Aquí está la clave para construir un traste. Según el musicólogo soviético L. A. Mazel, el intervalo del quinto, dividido en un cuarto y tono, es el principal elemento musical. Al elegir el tono como el modo principal de formación, los antiguos teóricos solo tienen que dejar de lado el sonido principal 
entonces otro tono 
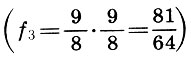y el intervalo restante entre el segundo tono y el tono cuarto 
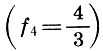llamada de medios tonos 
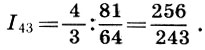Este nombre está bastante justificado, ya que dividir el intervalo de tonos a la mitad según la fórmula (6.12) da 
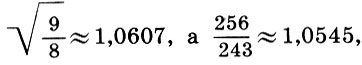es decir, un semitono es casi igual a medio tono * . Así se obtuvo la base de toda la música griega antigua - tetrachord - una escala de cuatro cuerdas dentro de un cuarto de galón.
* (El intervalo de tono (tono medio) en la teoría de la música se acepta como una unidad de medida aritmética de intervalos, y los intervalos de tono y tono medio, en contraste con sus coeficientes de intervalo, se denominan segundos grandes y pequeños ) .
Está claro que solo hay tres posibilidades para la posición del semitono dentro del tetracordio, que determinó la naturaleza y el nombre del tetracordio:
Dorian: tono medio - tono - tono;
Frigio: tono - semitono - tono;
Lydian: tono - tono - semitono .
Los nombres de los tetracords indican las regiones respectivas de Grecia y Asia Menor, cada una de las cuales cantaba en su propia armonía.
Por supuesto, cuatro cuerdas dentro de un cuarto de galón no fueron suficientes para dirigir la melodía, por lo que los tetracords se conectaron. Ya hemos descubierto que una octava consta de dos cuartos y un tono; , , . , , «». «» — . :
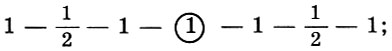
1 , 1/2 — , . . , , , (2 — , 3 — , - - - - - - c - o ), — * .
* ( «» , (1 — 1/2 — 1 — 1 — 1/2 — 1 — 1) , — . )
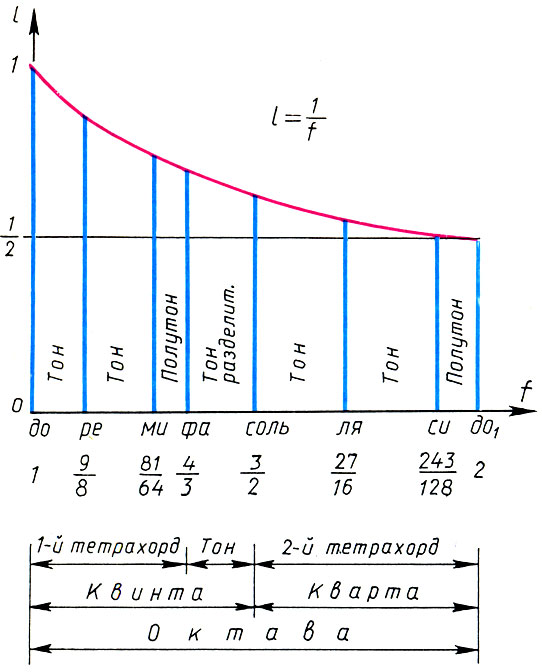Sistema de Pitágoras de la gama de Lidia y sus características matemáticas., , , , , . . . f 1 = 1, o : f 1 = 1, f 2 = 9 / 8 , f 3 = 9 / 8 * 9 / 8 = 81 / 64 , f 4 = 4 / 3 . : f 5 = 3 / 2f l = 3 / 2 , f 6 = 3 / 2 f 2 = 27 / 16 , f 7 = 3 / 2 f 3 = 243 / 128 , f 8 = 3 / 2 f 4 = 2. Finalmente, tenemos para coeficientes de intervalo
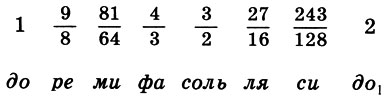(6.14)Este es el canon de Pitágoras. Según la leyenda, el canon de Pitágoras encontró su primera aplicación práctica en la afinación de la lira del legendario Orfeo.
. «» , . . , -(-), — - (-). 6 , (- — — ) . , . , , . , , . 1 , , , , — , . .
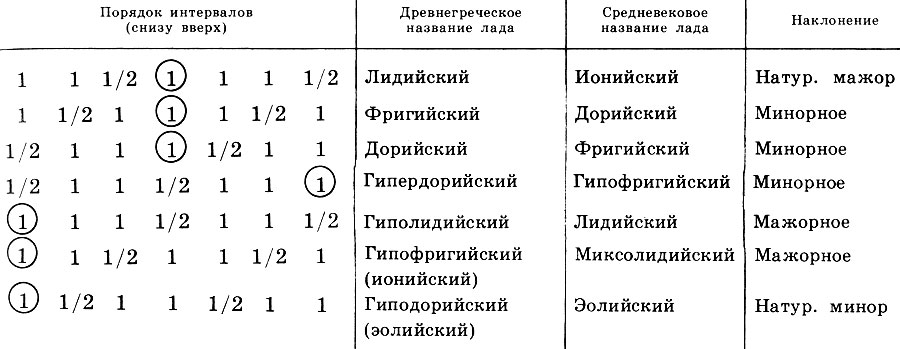Tabla 1. La secuencia de intervalos de tono (1) y semitono (1/2) en trastes antiguos (de abajo hacia arriba), nombres de trastes griegos y medievales antiguos y su inclinaciónSi recordamos que ahora solo dominan dos trastes, el mayor y el menor, solo podemos preguntarnos cuán sofisticada era la antigua conciencia musical. Los griegos llenaron cada camino con cierto contenido ético y estético, su "ethos", estableciendo una conexión clara entre las imágenes musicales y los estados del alma. Las funciones mágicas e incluso médicas se atribuyeron a la música, pero se le dio especial importancia a la música como medio de educación.
Bailando menada. Alivio, «» , . , , ,- (. 551-479 . . .), : « , — ». , , , . , , , , . , , , . , . , , . , , «» , , , , .
Aristóteles en política juzga los trastes, quizás incluso más estrictos que Platón, reconociendo solo el modo dórico como un modo capaz de entrenar la psique. Sin embargo, Aristóteles hace una clasificación "ética" detallada de los modos, distingue los modos que causan el equilibrio mental (Dorian), por el contrario, lo violan (hipofrigian - modo "mesa"), excitan la voluntad y el deseo de acción (hipodoriano - modo de tragedia griega), causar un estado extático y extático (frigio, hipolidiano).
Encontramos una hermosa descripción del "ethos" de los trastes griegos en el libro del antiguo escritor romano Apuleius (c. 124 -?) "Floridos": "Solía haber un flautista llamado Antigenides. Cada sonido en el juego de este músico era dulce, todos los trastes le eran familiares y él podía recrear para usted, según su elección, la simplicidad del traste eólico, la riqueza del jónico, la tristeza del lidio, la euforia del frigio y la militancia de Doria ".
Sin embargo, para! ¿Hay alguna contradicción aquí? ¡El estado de ánimo dórico se llama beligerante, pero de hecho es nuestro menor! Dado que era el estado de ánimo dórico el que se consideraba verdaderamente griego, resulta que el personaje principal de la música griega es triste, menor. Para los griegos, el humor dórico es una expresión de vivacidad, alegría e incluso militancia. Así explica el destacado erudito contemporáneo de la antigüedad, el último filósofo de la "edad de plata" rusa, el profesor A. F. Losev (1893-1988) * : "El arte griego es una afirmación invariable de la vida". La moderación noble e incluso la tristeza no dejan al griego incluso cuando se está divirtiendo, cuando está construyendo alegremente su vida, cuando está en guerra y muriendo. Los trastes “felices” de una forma u otra gravitan hacia este bello, noble, vigoroso, importante y al mismo tiempo majestuosamente triste, llorar: Dorian. El ambiente dórico es el estilo escultórico de la música griega ... Así que toda la escultura griega es tan reflexiva, triste y noble ".
* ( El destino de Aleksei Fedorovich Losev es feliz y trágico. Está feliz porque hasta el último día de su vida de 95 años Losev retuvo una capacidad de trabajo increíble y logró completar el trabajo principal: la "Historia de la estética antigua" de ocho volúmenes. Trágico, porque los otros ocho volúmenes de sus obras están escritos medio siglo antes (1927-1930), fueron anatematizados, y el autor mismo, siendo reprimido ilegalmente, continuó su investigación filosófica sobre la construcción del Canal del Mar Báltico Blanco, desde donde escribió: "Estoy encadenado cuando mi alma está hirviendo fuerzas eternas e inagotables ". Una de estas obras de Losev," La música como tema de la lógica ", podría servir de guía para este libro. Sin embargo, el destino de A.F. Losev es feliz, porque los manuscritos no se queman. Hoy, la gran herencia filosófica de A. F. Losev recupera su renacimiento. )
Pero, ¿qué pasa con el camino de Lidia? Después de todo, este es exactamente nuestro mayor, mientras que Apuleius lo llama triste y Platón: ¡funeral! Bueno, al evaluar el traste de Lidia, Aristóteles no estuvo de acuerdo con Platón, encontrando infantilismo ingenuo y encanto en el traste de Lidia y atribuyéndolo a trastes que causan equilibrio mental. Con el tiempo, el modo de Lidia ha perdido su carácter deplorable, y los antiguos teóricos comenzaron a hablar más a menudo sobre la "dulce melodía de Lidia" o la "melodía diversa de Lidia".
Por lo tanto, vemos que la cuestión del "ethos" de los trastes no se resuelve sin ambigüedades y está determinada en gran medida por la tradición de aplicar este o aquel traste. Y en nuestro tiempo, el oyente, criado, por ejemplo, en una música india sutil y peculiar, no distingue entre mayor y menor, sin mencionar su "ethos". Por supuesto, el estado de ánimo principal se distingue por tonos más claros y alegres, y hay razones objetivas para esto, que discutiremos en el capítulo 10. Pero la realización de estas posibilidades depende de una serie de otros factores (tempo, ritmo, patrón melódico, etc.), y por lo tanto hay muchas obras alegres y enérgicas en menor y triste, meditando en mayor. Recordemos al menos la "Patética Sonata" en menor Beethoven, este monólogo apasionado del Héroe, que llama a una batalla feroz e incluso la muerte. Muchos artistas recogieron muchos epítetos para esta sonata (aunque, quizás, el mejor de ellos, patético, pertenece al propio Beethoven), pero no se puede llamar triste solo: menor. Por el contrario, Nocturne No. 2 Op. El noveno piso mayor de Chopin está impregnado de un estado de ánimo de ensueño suave. Estos son recuerdos borrosos y tristes del autor, pero de ninguna manera una obra alegre, importante. En conclusión, tratemos de decir algunas palabras sobre el "ethos de los intervalos", porque el presente capítulo está dedicado al análisis de los intervalos musicales. Lo intentaremos, porque este tema es aún más controvertido y poco desarrollado que el "ethos de los trastes". Y aun así ...
Hasta ahora, no hemos dicho nada sobre la "consonancia más perfecta": prima (unísono) (l 2 / l 1 = 1, es decir, dos cuerdas producen un sonido de la misma altura), porque desde el punto de vista de las matemáticas este intervalo no es de interés. Sin embargo, en la orquesta, este intervalo más simple juega un papel muy importante, dando a este volumen de sonido y brillo.
La siguiente consonancia perfecta es la octava. Al mismo tiempo, la octava también da la impresión de un sonido tridimensional, y con un sonido secuencial, una sensación de amplitud y amplitud. Una excelente ilustración de esto es la "Canción de la Patria" del compositor I. O. Dunaevsky (1900-1955). En su coro ("De Moscú a las afueras ..."), una octava ascendente (l 1 / l 2 = 2) suena dos veces, pintando las vastas extensiones de nuestra Patria. Aquí, después de dos octavas, hay un quinto ascendente. Una quinta (l 1 / l 2 = 3/2) también suena amplia, pero más texturizada y dinámica que una octava.
Las melodías de muchas canciones e himnos revolucionarios comienzan con un intervalo de un cuarto ascendente (l 1 / l 2 = 4/3), por ejemplo, Internacional, Himno de la Unión Soviética, Marsellesa. Aquí, el intervalo de un cuarto suena resuelta y activamente, como un llamado a la acción.
Hay un "ethos" especial en el intervalo de un segundo: con un sonido simultáneo, es disonante y desagradable, pero con un sonido sucesivo el anterior se desborda en el siguiente, formando el flujo natural de la melodía de un sonido a otro. En una melodía, los intervalos entre dos sonidos de referencia a menudo se completan en segundos intervalos consecutivos. Por ejemplo, la canción "A Birch Stood in the Field" comienza con un quinto intervalo lleno de segundos consecutivos, que da la impresión de un flujo tranquilo y majestuoso de la melodía, como imágenes majestuosas y tranquilas de la naturaleza rusa.
Y lo más desagradable y disonante es el intervalo tritón o semioctava (l 1 / l 2 = ) Por su inconsistencia, este intervalo "incitó" al Arquitecto a una "prueba musical" de irracionalidad .
Gracias a la Biblioteca de Matemáticas por digitalizar el libro.