Richard Hamming: Capítulo 10. Teoría de la codificación - I

"El objetivo de este curso es prepararte para tu futuro técnico".

Hola Habr ¿Recuerdas el increíble artículo "Tú y tu trabajo" (+219, 2442 marcadores, 394k lecturas)?

Entonces, Hamming (sí, sí, los códigos de Hamming que se autoverifican y corrigen a sí mismos) tiene un libro completo escrito basado en sus conferencias. Lo estamos traduciendo, porque el hombre está hablando de negocios.

Este libro no es solo sobre TI, es un libro sobre el estilo de pensamiento de personas increíblemente geniales. “Esto no es solo una carga de pensamiento positivo; describe condiciones que aumentan las posibilidades de hacer un gran trabajo ".

Ya hemos traducido 28 (de 30) capítulos. Y estamos trabajando en una edición en papel.

Teoría de la codificación - I

Habiendo considerado las computadoras y el principio de su trabajo, ahora consideraremos el tema de la información: cómo las computadoras representan la información que queremos procesar. El significado de cualquier carácter puede depender de cómo se procese, la máquina no tiene un significado específico para el bit utilizado. Cuando discutimos la historia del software, Capítulo 4, consideramos un lenguaje de programación sintético, en el que el código de la instrucción break coincidía con el código de otras instrucciones. Esta situación es típica para la mayoría de los idiomas, el significado de la instrucción está determinado por el programa correspondiente.

Para simplificar el problema de presentar información, consideramos el problema de transmitir información de punto a punto. Esta pregunta está relacionada con el tema de la información de conservación. Los problemas de transmisión de información en el tiempo y el espacio son idénticos. La figura 10.1 muestra un modelo estándar para transmitir información.



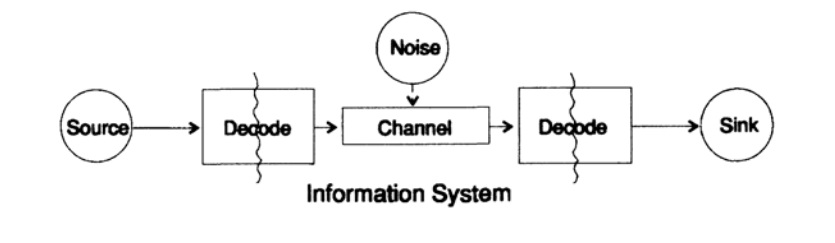Figura 10.1

A la izquierda en la figura 10.1 se encuentra la fuente de información. Cuando consideramos el modelo, no nos importa la naturaleza de la fuente. Puede ser un conjunto de símbolos del alfabeto, números, fórmulas matemáticas, notas musicales, símbolos con los que podemos representar movimientos de baile; la naturaleza de la fuente y el significado de los símbolos almacenados en ella no forma parte del modelo de transmisión. Consideramos solo la fuente de información, con tal restricción obtenemos una poderosa teoría general que puede extenderse a muchas áreas. Es una abstracción de muchas aplicaciones.

Cuando Shannon creó la teoría de la información a fines de la década de 1940, se creía que debería llamarse la teoría de la comunicación, pero insistió en el término información. Este término se ha convertido en una causa constante de un mayor interés y una constante decepción en teoría. Los investigadores querían construir "teorías de información" completas, degeneraron en una teoría de un conjunto de personajes. Volviendo al modelo de transmisión, tenemos una fuente de datos que necesita ser codificada para la transmisión.

El codificador consta de dos partes, la primera parte se llama codificador fuente, el nombre exacto depende del tipo de fuente. Las fuentes de diferentes tipos de datos corresponden a diferentes tipos de codificadores.

La segunda parte del proceso de codificación se denomina codificación de canal y depende del tipo de canal para transmitir datos. Por lo tanto, la segunda parte del proceso de codificación es consistente con el tipo de canal de transmisión. Por lo tanto, cuando se utilizan interfaces estándar, los datos de la fuente se codifican inicialmente de acuerdo con los requisitos de la interfaz, y luego de acuerdo con los requisitos del canal de datos utilizado.

Según el modelo, en la figura 10.1, el canal de datos está expuesto a "ruido aleatorio adicional". Todo el ruido en el sistema se combina en este punto. Se supone que el codificador acepta todos los caracteres sin distorsión, y el decodificador realiza su función sin errores. Esta es una idealización, pero para muchos propósitos prácticos está cerca de la realidad.

La fase de decodificación también consta de dos etapas: canal - estándar, estándar - receptor de datos. Al final de la transferencia de datos se transmite al consumidor. Y nuevamente, no estamos considerando cómo el consumidor interpreta estos datos.

Como se señaló anteriormente, un sistema de transmisión de datos, por ejemplo, mensajes telefónicos, radio, programas de televisión, presenta datos en forma de un conjunto de números en los registros de una computadora. Repito nuevamente, la transmisión en el espacio no es diferente de la transmisión en el tiempo o el almacenamiento de información. ¿Tiene información que se requerirá después de un tiempo, luego debe codificarse y almacenarse en la fuente de almacenamiento de datos. Si es necesario, la información se decodifica. Si el sistema de codificación y decodificación es el mismo, transmitimos datos a través del canal de transmisión sin cambios.

La diferencia fundamental entre la teoría presentada y la teoría habitual en física es la suposición de que no hay ruido en la fuente y el receptor. De hecho, se producen errores en cualquier equipo. En mecánica cuántica, el ruido ocurre en cualquier etapa de acuerdo con el principio de incertidumbre, y no como una condición inicial; En cualquier caso, el concepto de ruido en la teoría de la información no es equivalente a un concepto similar en mecánica cuántica.
Para mayor claridad, consideraremos la forma binaria de representación de datos en el sistema. Otros formularios se procesan de manera similar, por simplicidad no los consideraremos.

Comenzamos nuestra consideración de los sistemas con caracteres codificados de longitud variable, como en el código Morse clásico de puntos y guiones, en el que los caracteres que aparecen con frecuencia son cortos y los raros son largos. Este enfoque le permite lograr una alta eficiencia del código, pero vale la pena señalar que el código Morse es ternario, no binario, ya que contiene un espacio entre puntos y guiones. Si todos los caracteres en el código tienen la misma longitud, dicho código se llama código de bloque.

La primera propiedad obvia necesaria del código es la capacidad de decodificar de manera única el mensaje en ausencia de ruido, al menos esta parece ser la propiedad deseada, aunque en algunas situaciones este requisito puede ser descuidado. Los datos del canal de transmisión para el receptor se ven como una secuencia de caracteres de ceros y unos.

Llamaremos a dos caracteres adyacentes una extensión doble, tres caracteres adyacentes a una extensión triple y, en el caso general, si reenviamos N caracteres, el receptor ve adiciones al código base de N caracteres. El receptor, sin conocer el valor de N, debe dividir la secuencia en bloques de difusión. O, en otras palabras, el receptor debe poder descomponer la secuencia de manera única para restaurar el mensaje original.

Considere un alfabeto de una pequeña cantidad de caracteres, generalmente los alfabetos son mucho más grandes. Los alfabetos de idiomas comienzan de 16 a 36 caracteres, incluidos mayúsculas y minúsculas, signos numéricos, signos de puntuación. Por ejemplo, en la tabla ASCII 128 = 2 ^ 7 caracteres.
Considere un código especial que consta de 4 caracteres s1, s2, s3, s4

s1 = 0; s2 = 00; s3 = 01; s4 = 11.

¿Cómo debe interpretar el receptor la siguiente expresión recibida?

0011 ?

¿Cómo s1s1s4 o cómo s2s4 ?

No puede dar una respuesta inequívoca a esta pregunta, este código definitivamente no está decodificado, por lo tanto, no es satisfactorio. Código, por otro lado

s1 = 0; s2 = 10; s3 = 110; s4 = 111

decodifica el mensaje de una manera única. Tome una cadena arbitraria y considere cómo la decodificará el receptor. Necesita construir un árbol de decodificación De acuerdo con el formulario en la Figura 10.II. Cadena

1101000010011011100010100110 ...

puede dividirse en bloques de caracteres

110, 10, 0, 10, 0, 110, 111, 0, 0, 0, 10, 10, 0, 110, ...

de acuerdo con la siguiente regla para construir un árbol de decodificación:

Si estás en la parte superior del árbol, lee el siguiente personaje. Cuando alcanzas la hoja de un árbol, conviertes la secuencia a un personaje y vuelves al inicio.

La razón de la existencia de tal árbol es que ningún personaje es un prefijo del otro, por lo que siempre se sabe cuándo debe volver al comienzo del árbol de decodificación.

Es necesario prestar atención a lo siguiente. En primer lugar, la decodificación es un proceso estrictamente continuo, en el que cada bit se examina solo una vez. En segundo lugar, los protocolos generalmente incluyen caracteres que son un marcador del final del proceso de decodificación y son necesarios para indicar el final de un mensaje.

No utilizar un carácter final es un error común en el diseño del código. Por supuesto, puede proporcionar un modo de decodificación constante, en cuyo caso no se necesita el carácter final.



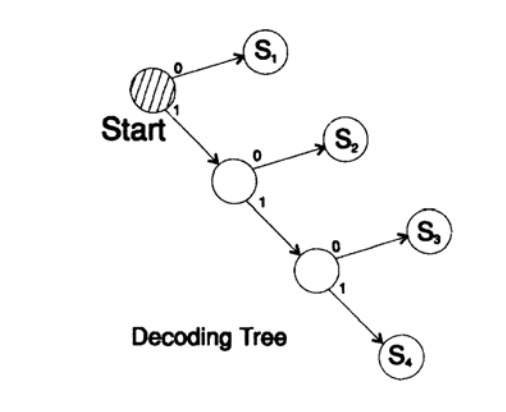Figura 10.II

La siguiente pregunta son los códigos para la decodificación de flujo (instantáneo). Considere el código que se obtiene del anterior mostrando caracteres

s1 = 0; s2 = 01; s3 = 011; s4 = 111.

Supongamos que obtenemos la secuencia 011111 ... 111 . La única forma en que puede decodificar el texto del mensaje es agrupar bits del final de 3 en un grupo y seleccionar grupos con un cero inicial delante de unos, después de lo cual puede decodificar. Tal código se decodifica de una manera única, ¡pero no al instante! ¡Para decodificar, debe esperar el final de la transferencia! En la práctica, este enfoque elimina la tasa de decodificación (teorema de Macmillan), por lo tanto, es necesario buscar métodos de decodificación instantánea.

Considere dos formas de codificar el mismo carácter, Si:

s1 = 0; s2 = 10; s3 = 110; s4 = 1110, s5 = 1111,

El árbol de decodificación de este método se muestra en la Figura 10.III.



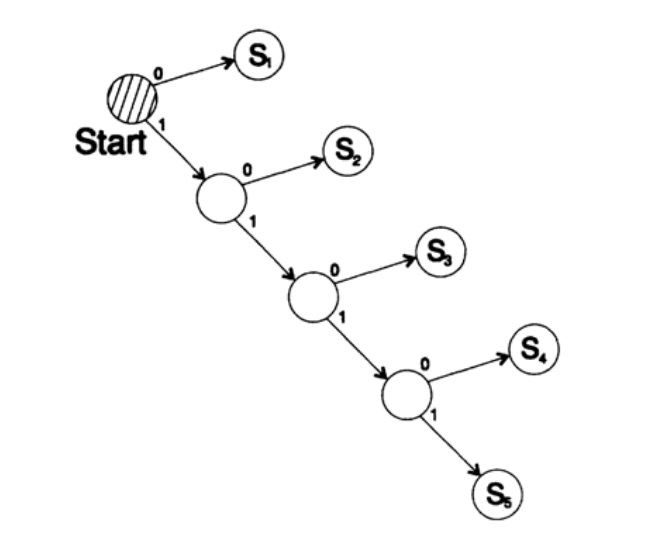Figura 10.III

Segunda forma

s1 = 00; s2 = 01; s3 = 100; s4 = 110, s5 = 111 ,

El árbol de decodificación de este cuidado se muestra en la Figura 10.IV.

La forma más obvia de medir la calidad del código es la longitud promedio de un conjunto de mensajes. Para esto, es necesario calcular la longitud del código de cada carácter multiplicado por la probabilidad correspondiente de ocurrencia de pi. Por lo tanto, se obtiene la longitud del código completo. La fórmula para la longitud promedio L del código para un alfabeto de q caracteres es la siguiente



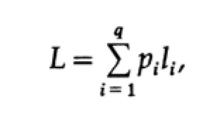
donde pi es la probabilidad de aparición del símbolo si, li es la longitud correspondiente del símbolo codificado. Para un código eficiente, el valor de L debe ser lo más pequeño posible. Si P1 = 1/2, p2 = 1/4, p3 = 1/8, p4 = 1/16 y p5 = 1/16, entonces para el código # 1 obtenemos el valor de longitud del código



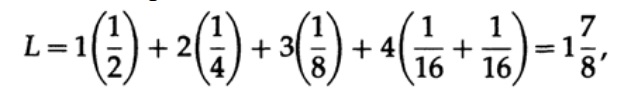
Y para el código # 2



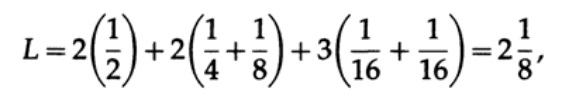
Los valores obtenidos indican la preferencia del primer código.
Si todas las palabras del alfabeto tienen la misma probabilidad de ocurrencia, entonces el segundo código será más preferible. Por ejemplo, con pi = 1/5, código de longitud # 1



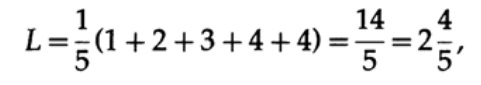
y longitud del código # 2



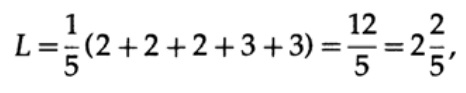
Este resultado muestra una preferencia por 2 códigos. Por lo tanto, cuando se desarrolla un código "bueno", es necesario tener en cuenta la probabilidad de aparición de caracteres.



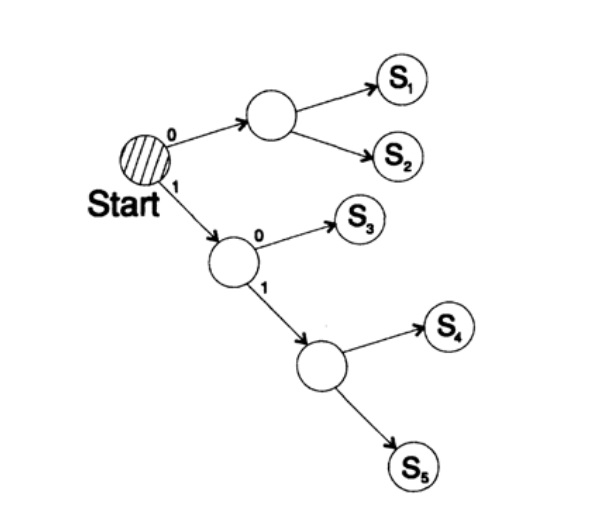Figura 10.IV



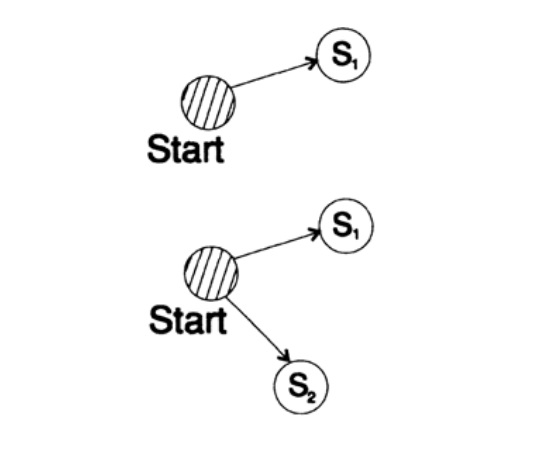Figura 10.V

Considere la desigualdad de Kraft, que determina el valor límite de la longitud del código del símbolo li. En la base 2, la desigualdad se representa como



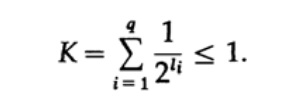
Esta desigualdad sugiere que el alfabeto no puede tener demasiados caracteres cortos, de lo contrario la suma será bastante grande.

Para demostrar la desigualdad de Kraft para cualquier código decodificado único rápido, construimos un árbol de decodificación y aplicamos el método de inducción matemática. Si un árbol tiene una o dos hojas, como se muestra en la Figura 10.V, entonces la desigualdad es sin duda cierta. Además, si el árbol tiene más de dos hojas, dividimos el árbol de largo m en dos subárboles. De acuerdo con el principio de inducción, suponemos que la desigualdad es verdadera para cada rama de altura m -1 o menos. Según el principio de inducción, aplicando desigualdad a cada rama. Denote las longitudes de los códigos de las ramas K 'y K' '. Cuando se combinan dos ramas de un árbol, la longitud de cada una aumenta en 1, por lo tanto, la longitud del código consiste en las sumas K '/ 2 y K' '/ 2,



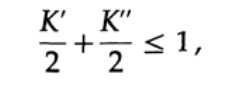
El teorema está probado.

Considere la prueba del teorema de Macmillan. Aplicamos la desigualdad de Kraft para decodificar códigos sin hilos. La prueba se basa en el hecho de que para cualquier número K> 1, la enésima potencia del número es obviamente más que una función lineal de n, donde n es un número bastante grande. Elevamos la desigualdad de Kraft a la enésima potencia y presentamos la expresión como una suma



donde Nk es el número de caracteres de longitud k, la suma comienza con la longitud mínima de la enésima representación del carácter y termina con la longitud máxima nl, donde l es la longitud máxima del carácter codificado. Del requisito de decodificación única se deduce eso. El importe se presenta como



Si K> 1, entonces es necesario establecer n lo suficientemente grande como para que la desigualdad se vuelva falsa. Por lo tanto, k <= 1; El teorema de Macmillan está probado.

Considere algunos ejemplos de la aplicación de la desigualdad de Kraft. ¿Puede existir un código decodificado de forma única con longitudes 1, 3, 3, 3? Si desde



¿Qué pasa con las longitudes 1, 2, 2, 3? Calcular de acuerdo con la fórmula



¡Desigualdad violada! Hay demasiados caracteres cortos en este código.

Los códigos de coma son códigos que consisten en los caracteres 1, que terminan en un carácter 0, con la excepción del último carácter que consiste en todos. Uno de los casos especiales es el código.

s1 = 0; s2 = 10; s3 = 110; s4 = 1110; s5 = 11111.

Para este código, obtenemos la expresión para la desigualdad de Kraft



En este caso, logramos la igualdad. Es fácil ver que para los códigos de puntos, la desigualdad de Kraft degenera en igualdad.

Al crear un código, debe prestar atención a la cantidad de Kraft. Si la cantidad de Kraft comienza a exceder 1, entonces esta es una señal sobre la necesidad de incluir un carácter de una longitud diferente para reducir la longitud promedio del código.

Cabe señalar que la desigualdad de Kraft no significa que este código sea decodificable de manera única, sino que existe un código con caracteres de tal longitud que está decodificado de manera única. Para construir un código decodificado único, puede asignar la longitud correspondiente en bits li con un número binario. Por ejemplo, para longitudes 2, 2, 3, 3, 4, 4, 4, 4, obtenemos la desigualdad de Kraft



Por lo tanto, puede existir un código de flujo decodificado único.

s1 = 00; s2 = 01; s3 = 100; s4 = 101;

s5 = 1100; s6 = 1101; s7 = 1110; s8 = 1111;

Quiero prestar atención a lo que realmente sucede cuando intercambiamos ideas. Por ejemplo, en este momento quiero transferir la idea de mi cabeza a la tuya. Pronuncio algunas palabras a través de las cuales, como creo, puedes entender (entender) esta idea.

Pero cuando un poco más tarde desee transmitir esta idea a su amigo, seguramente pronunciará palabras completamente diferentes. De hecho, el significado o significado no está encerrado en ninguna palabra específica. Usé algunas palabras, y puedes usar palabras completamente diferentes para transmitir la misma idea. Por lo tanto, diferentes palabras pueden transmitir la misma información. Pero, tan pronto como le diga a su interlocutor que no comprende el mensaje, entonces, por regla general, el interlocutor seleccionará un conjunto diferente de palabras, la segunda o incluso la tercera, para transmitir el significado. Por lo tanto, la información no está encerrada en un conjunto de palabras específicas. Tan pronto como reciba estas o esas palabras, hará mucho trabajo al traducir las palabras a la idea que el interlocutor quiere transmitirle.

Aprendemos a seleccionar palabras para adaptarnos al interlocutor. En cierto sentido, elegimos palabras que coincidan con nuestros pensamientos y el nivel de ruido en el canal, aunque dicha comparación no refleja con precisión el modelo que uso para representar el ruido en el proceso de decodificación. En organizaciones grandes, un problema grave es la incapacidad del interlocutor para escuchar lo que otra persona ha dicho. En puestos superiores, los empleados escuchan lo que "quieren escuchar". En algunos casos, debe recordar esto cuando asciende en la escala profesional. La presentación de información en una forma formal es un reflejo parcial de los procesos de nuestras vidas y ha encontrado una amplia aplicación más allá de los límites de las reglas formales en las aplicaciones informáticas.

Continuará ...

¿Quién quiere ayudar con la traducción, el diseño y la publicación del libro? Escriba en un correo electrónico personal o correo magisterludi2016@yandex.ru

Por cierto, también lanzamos la traducción de otro libro genial: "La máquina de los sueños: la historia de la revolución informática" )