Redes neuronales capsulares

En 2017, Jeffrey Hinton (uno de los fundadores del enfoque de propagación por error de retorno) publicó un artículo que describe las redes neuronales capsulares y propone un algoritmo para el enrutamiento dinámico entre cápsulas para enseñar la arquitectura propuesta.

Las redes neuronales convolucionales clásicas tienen desventajas. La representación interna de datos de redes neuronales convolucionales no tiene en cuenta las jerarquías espaciales entre objetos simples y complejos. Por lo tanto, si los ojos, la nariz y los labios para una red neuronal convolucional se muestran aleatoriamente en la imagen, este es un claro signo de la presencia de una cara. Y la rotación del objeto afecta la calidad del reconocimiento, mientras que el cerebro humano resuelve fácilmente este problema.


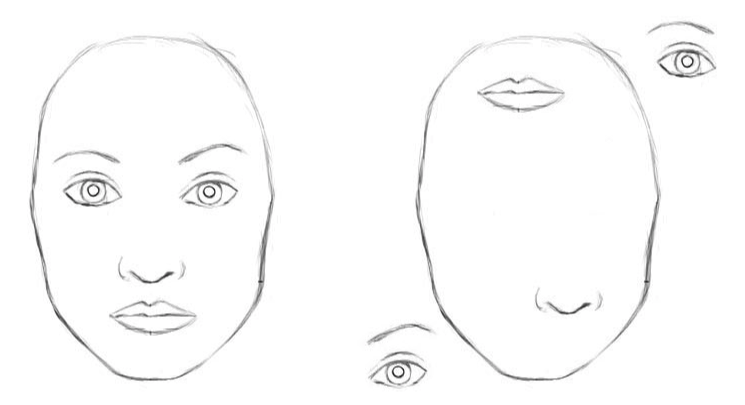
Para una red neuronal convolucional, 2 imágenes son similares [2]


Se necesitarán miles de ejemplos para entrenar el reconocimiento de objetos desde varios ángulos de CNN.


Las redes de cápsulas reducen el error de reconocimiento de un objeto desde otro ángulo en un 45%.

Cápsulas de prescripción

Las cápsulas encapsulan información sobre el estado de la función, que se encuentra en forma de vector. Las cápsulas codifican la probabilidad de detectar un objeto como la longitud del vector de salida. El estado de la función detectada se codifica como la dirección en la que apunta el vector ("parámetros de creación de instancia"). Por lo tanto, cuando la función detectada se mueve a través de la imagen o el estado de la imagen cambia, la probabilidad permanece sin cambios (la longitud del vector no cambia), pero la orientación cambia.

Imagine que una cápsula detecta una cara en una imagen y genera un vector 3D de longitud 0.99. Luego, mueva la cara en la imagen. El vector rotará en su espacio, representando un estado cambiante, pero su longitud permanecerá fija porque la cápsula confía en que ha detectado una cara.



Diferencias entre cápsulas y neuronas. [2]

Una neurona artificial se puede describir en tres pasos:

1. ponderación escalar de escalares de entrada
2. suma de escalares de entrada ponderados
3. transformación escalar no lineal.

La cápsula tiene las formas vectoriales de los 3 pasos anteriores, además de la nueva fase de la transformación afín de entrada:

1. multiplicación matricial de vectores de entrada
2. ponderación escalar de vectores de entrada
3. suma de vectores de entrada ponderados
4. no linealidad vectorial.

Otra innovación introducida en CapsNet es una nueva función de activación no lineal que toma un vector y luego "da" su longitud no más de 1, pero no cambia de dirección.



El lado derecho de la ecuación (rectángulo azul) escala el vector de entrada para que el vector tenga una longitud de bloque, y el lado izquierdo (rectángulo rojo) realiza una escala adicional.

El diseño de la cápsula se basa en la construcción de una neurona artificial, pero la extiende a una forma vectorial para proporcionar capacidades representativas más potentes. Los pesos de matriz también se introducen para codificar relaciones jerárquicas entre entidades de diferentes capas. La equivalencia de la actividad neuronal se logra en relación con los cambios en los datos de entrada y la invariancia en las probabilidades de detectar signos.

Enrutamiento dinámico entre cápsulas.

El algoritmo de enrutamiento dinámico [1].

La primera línea dice que este procedimiento toma cápsulas en el nivel inferior l y sus salidas u_hat, así como el número de iteraciones de enrutamiento r. La última línea dice que el algoritmo producirá la salida de una cápsula de nivel superior v_j.

La segunda línea contiene un nuevo coeficiente b_ij, que no hemos visto antes. Este coeficiente es un valor temporal que se actualizará de forma iterativa y, una vez completado el procedimiento, su valor se almacenará en c_ij. Al comienzo del entrenamiento, el valor de b_ij se inicializa a cero.

La línea 3 dice que los pasos 4-7 se repetirán r veces.
El paso en la línea 4 calcula el valor del vector c_i, que es todos los pesos de enrutamiento para la cápsula inferior i.

Después de calcular los pesos c_ij para las cápsulas del nivel inferior, vaya a la línea 5, donde observamos las cápsulas de un nivel superior. Este paso calcula una combinación lineal de vectores de entrada ponderados utilizando los coeficientes de enrutamiento c_ij definidos en el paso anterior.

Luego, en la línea 6, los vectores del último paso pasan a través de una transformación no lineal, que garantiza la dirección del vector, pero su longitud no debe exceder 1. Este paso crea el vector de salida v_j para todos los niveles superiores de la cápsula. [2]
La idea básica es que la similitud entre entrada y salida se mide como el producto escalar entre la entrada y la salida de la cápsula, y luego cambia el coeficiente de enrutamiento. La mejor práctica es usar tres iteraciones de enrutamiento.

Conclusión

Las redes neuronales capsulares son una arquitectura prometedora de redes neuronales que mejora el reconocimiento de imágenes con ángulos cambiantes y estructura jerárquica. Las redes neuronales capsulares se entrenan mediante el enrutamiento dinámico entre cápsulas. Las redes de cápsulas reducen el error de reconocimiento de un objeto desde un ángulo diferente en un 45% en comparación con CNN.