¿Qué pasó con la paradoja de Fermi?

La paradoja de Fermi es que la probabilidad de una civilización extraterrestre generalmente se estima bastante alta, y no hay nada que vea signos de su existencia. Recientemente, apareció una preimpresión de Sanders y coautores de "Disolución de la paradoja de Fermi" en arxiv, que ya han interpretado como la cancelación de esta paradoja (verdadera), charla ociosa en ausencia de datos (bastante cierto, pero cierto para la paradoja de Fermi en general, y no solo para este artículo) , y como evidencia de la inexistencia de extraterrestres y / o baja L (falsedad). En este artículo, intentaremos averiguar qué contiene realmente la preimpresión.

Que pasa

En primer lugar, la ecuación de Drake en sí. Se presenta en el KDPV; el último factor es una broma, y ​​el resto debe entenderse de la siguiente manera: en el universo observable (o nuestra galaxia, o cualquier otro volumen de espacio) $$ estrellas Cada estrella con probabilidad $$ tiene planetas Es probable que cada uno de estos planetas $$ ubicado en la zona de Ricitos de Oro, tiene una composición química adecuada, etc. En cada planeta que sea potencialmente capaz de sostener la vida con probabilidad $$ (por unidad de tiempo) surge una vida que es probable $$ alcanza razonabilidad y con probabilidad $$ se pone en contacto Y finalmente, cualquier especie inteligente que surge existe $$ años desde el nacimiento hasta la extinción. Si multiplica todo esto, obtiene el número de especies inteligentes en esta área.

El tiempo entre el origen de la mente y la aparición de una civilización notable a distancias interestelares se descuida. En el caso de la Tierra, por ejemplo, miles de millones de años han pasado desde la aparición del planeta hasta la aparición de la vida y desde la aparición de la vida hasta la aparición de la especie Homo sapiens . El progreso tecnológico es incomparablemente más rápido: la aparición del Homo sapiens del mensaje de Arecibo separa menos de diez millones de años. La colonización interestelar aún no ha comenzado, pero este es también el peor caso de un par de millones de años. En comparación con las etapas pre-tecnológicas, dentro del margen de error.

Lo cual, para decirlo con más tacto, es bastante alto . Desde el orden de magnitud para el número de estrellas y la probabilidad de tener planetas de hasta 200 órdenes de magnitud (doscientos órdenes de magnitud, las estimaciones difieren en $$ veces) para la probabilidad de abiogénesis. Este trabajo ingrato es evaluar las probabilidades de una sola observación. Sin embargo, los científicos publicaron varias estimaciones. $$ y la mayoría de las veces llegué a la conclusión de que $$ e incluso $$ . Lo que, de hecho, es la paradoja de Fermi: según nuestras mejores estimaciones, debe haber otras razas inteligentes en la galaxia, y no había evidencia confiable de su existencia.

El problema, obviamente, no está en la galaxia: si las estimaciones difieren de la realidad observada, peor aún para las estimaciones. Cualquiera de los parámetros está sobreestimado ( y Dios nos bendiga, si es L ), o de alguna manera pensamos incorrectamente. Sandberg et al están abogando por la última versión.

¿Y cómo contar correctamente?

Parecería multiplicar un puñado de números reales, no el binomio de Newton. El problema es que en tal situación, la multiplicación de números se basa en el supuesto de que, de todos modos, los conocemos con precisión. Como vimos anteriormente, esta suposición está muy lejos de la realidad.

Considere un ejemplo simplificado: deje que la ecuación de Drake tenga nueve parámetros y los nueve se distribuyan uniformemente en el rango $$ . La mejor estimación puntual para cada parámetro es 0.1 y su producto da una probabilidad de una civilización por billón de estrellas. En la galaxia de $$ algo así como 100 civilizaciones deberían aparecer en las estrellas, y la probabilidad de que esto nunca suceda $$ . Tales probabilidades generalmente se ilustran con frases como "si cada átomo en <algo muy grande como el sistema solar> durante <algún tiempo muy largo como su edad>". Lo que en este caso parece bastante apropiado, pero de hecho es imposible no rechazar una hipótesis tan nula. La paradoja de Fermi se eleva a toda su altura.

Si no usamos estimaciones puntuales, y para cada parámetro tomamos un valor aleatorio del rango correspondiente, entonces la galaxia está vacía en el 21.45% de las simulaciones. El hecho de que algo sucedió con una probabilidad de poco más de un quinto no es en absoluto una paradoja. Esto es un poco menos probable de que un par de reyes derroten a todas las demás manos en una mesa de Hold'em de 9 jugadores , y con los reyes de bolsillo personalmente voy todo adentro en la primera oportunidad.

La misma lógica se puede aplicar a las estimaciones reales de los parámetros de la ecuación de Drake. Si los recopila de la literatura y ejecuta la simulación, obtendrá la siguiente imagen:



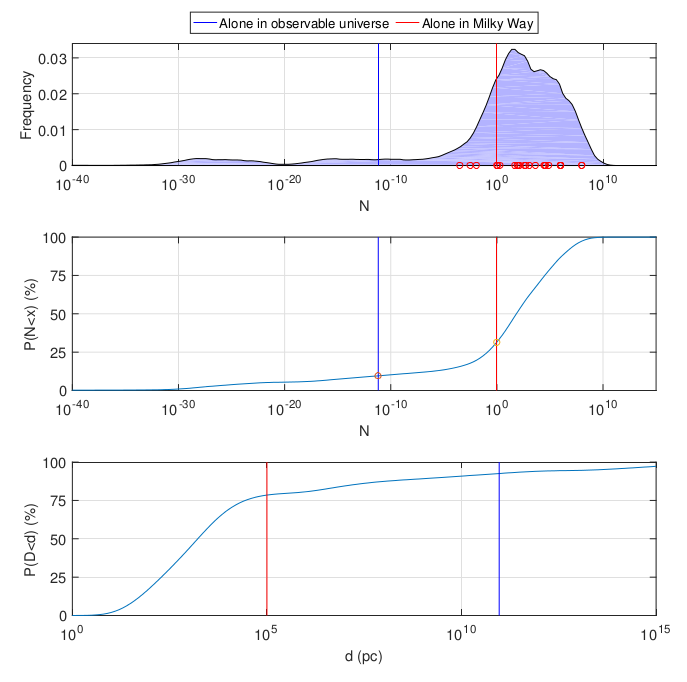
De arriba a abajo: la función de densidad de probabilidad para el número de civilizaciones en nuestra galaxia, la densidad de distribución acumulada para ella, la densidad de distribución acumulada de la distancia a la civilización observable más cercana en parsecs. Todo está en una escala logarítmica. Las líneas rojas y azules indican la probabilidad de que seamos la única civilización en nuestra galaxia y el universo observable. Círculos en el gráfico superior: clasificaciones literarias normalizadas $$ .

En general, el resultado es bastante optimista: la mayor densidad de probabilidad recae en la multiplicidad de civilizaciones (promedio de 53 millones, mediana de 100). Pero para los propósitos de la paradoja de Fermi, las cifras son aproximadamente las mismas que en un ejemplo simplificado: con una probabilidad del veinte por ciento o algo así, la Vía Láctea contiene solo una civilización (la nuestra). Por cierto, una consecuencia bastante contraintuitiva: la probabilidad de que la Vía Láctea, sin contar la Tierra , contenga exactamente una civilización (excepto la nuestra) es prácticamente la misma.

En lugar de tomar estimaciones de parámetros directamente de la literatura, las distribuciones se pueden construir y calcular analíticamente. Se toma un rango de estimaciones hasta un orden de magnitud y cada parámetro se considera log-normal o log-uniformemente distribuido en el intervalo correspondiente. El resultado se desplaza un poco hacia la izquierda, pero el significado es el mismo:



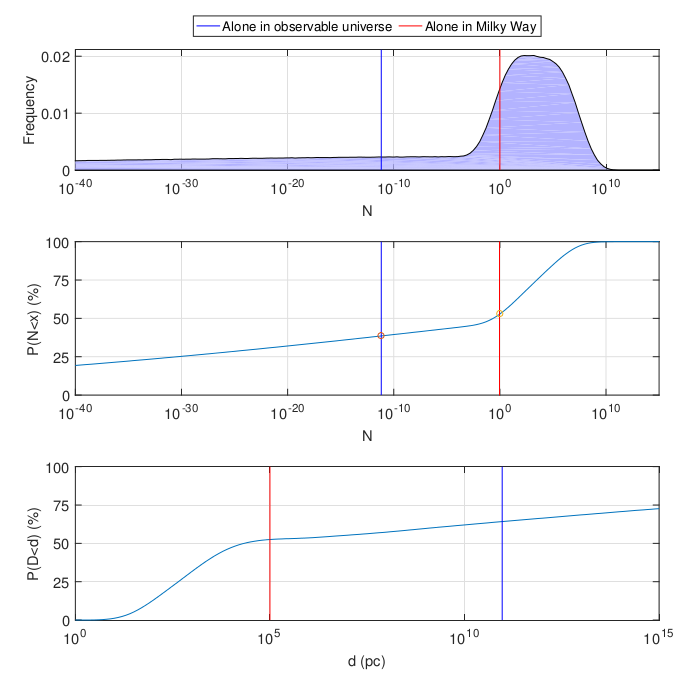
¿Qué significa todo esto? La respuesta correcta a la pregunta "¿hay vida en el universo o no?" Sigue siendo "No lo sé". Cuán agradablemente elegantes las estadísticas bayesianas cuestan poco en ausencia de datos experimentales. La respuesta a la pregunta "¿Cuánto debería sorprendernos de lo que se ha observado ha cambiado? $$ " Solía ​​ser "Muy fuerte, así que o la vida es algo muy raro, o todos moriremos en una guerra nuclear o algo así ", y ahora se ha convertido en "Bueno, en principio, no es muy probable, pero nada extraordinario". La probabilidad de una guerra nuclear y / o una reunión con un dinosaurio sobre los extraterrestres de Nevsky solo disminuyó en el sentido bayesiano: estamos un poco menos seguros de que esto suceda. Si estos eventos realmente suceden o no depende de los factores del mundo real (aproximadamente, Putin, Trump y Zorblaks, el comedor galáctico), y no las matemáticas utilizadas para discutirlos.