Codificadores automáticos e inteligencia artificial fuerte

La teoría de los codificadores automáticos y los modelos de generación se ha desarrollado recientemente, pero se dedican bastantes trabajos a cómo usarlos en problemas de reconocimiento. Al mismo tiempo, la propiedad de los autoencoders para obtener un modelo de datos paramétricos ocultos y las consecuencias matemáticas de esto permiten asociarlos con los métodos bayesianos de toma de decisiones.

El artículo propone un aparato matemático original "un conjunto de codificadores automáticos con un espacio latente común", que le permite extraer conceptos abstractos de los datos de entrada y demuestra la capacidad de "aprendizaje de una sola vez". Además, se puede utilizar para superar muchos de los problemas fundamentales de los algoritmos modernos de aprendizaje automático basados ​​en redes multicapa y el enfoque de "aprendizaje profundo".

Antecedentes

Las redes neuronales artificiales, entrenadas utilizando el mecanismo de propagación hacia atrás de errores, casi reemplazaron otros enfoques en muchos problemas de reconocimiento y estimación de parámetros. Pero tienen una serie de inconvenientes que, al parecer, no se pueden eliminar sin una revisión seria del enfoque:

1. inestabilidad extrema para ingresar datos que no se encuentran en la muestra de entrenamiento (incluso en el caso de ataques adversos)
   
   
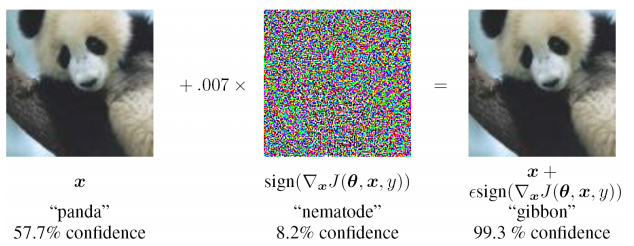
2. es difícil evaluar la fuente del problema y volver a entrenar localmente en uno de los niveles (solo tiene que complementar la muestra de entrenamiento y volver a entrenar), es decir problema de caja negra
3. no se proporciona la posibilidad de diferentes interpretaciones de la misma información de entrada, se ignora la naturaleza estadística de los datos observados
   
   

Al estar involucrado en la resolución de problemas aplicados, y confiando en una serie de trabajos existentes, propongo un enfoque que es notablemente diferente de los existentes, elimina algunas de sus deficiencias y es aplicable para resolver problemas aplicados en diversas áreas del aprendizaje automático.

Codificador automático para estimar la densidad de distribución

En la teoría de la toma de decisiones, un lugar muy importante está ocupado por la densidad de distribución (o función de distribución) de variables aleatorias. Es necesario tener estimaciones de las funciones de distribución para calcular el riesgo posterior.

Resulta que los codificadores automáticos son muy naturales para evaluar las funciones de distribución. Esto puede explicarse de la siguiente manera: el conjunto de datos de entrenamiento está determinado por la densidad de su distribución. Cuanto mayor sea la densidad de ejemplos de entrenamiento alrededor de un punto local en el espacio de entrada, mejor será el auto-codificador que reconstruye el vector de entrada en esta ubicación en el espacio. Además, dentro del autoencoder hay un vector de representación latente de los datos de entrada (generalmente de baja dimensión), y si los datos se proyectan en el espacio latente en un área que no se utilizó anteriormente en el entrenamiento, entonces no había nada similar en la muestra de entrenamiento.

Hay una serie de trabajos cerrados y algo aislados:

1. Alain, G. y Bengio, Y. Lo que los autoencoders regularizados aprenden de la distribución de generación de datos. 2013
2. Kamyshanska, H. 2013. Sobre la puntuación del autoencoder
3. Daniel Jiwoong Im, Mohamed Ishmael Belghazi, Roland Memisevic. 2016. Conservación de los codificadores automáticos desatados

El primero justifica que el resultado de la reconstrucción de Denoising de codificadores automáticos está relacionado con la función de densidad de probabilidad de los datos de entrada, pero se imponen varias restricciones a los codificadores automáticos. El segundo contiene requisitos suficientes para el codificador automático: los pesos del codificador y del decodificador deben estar "conectados", es decir La matriz de peso de la capa del codificador es la matriz transpuesta del decodificador. En el último trabajo, se investigan más a fondo las condiciones necesarias y suficientes para el hecho de que el codificador automático está asociado con una densidad de probabilidad.

Estos trabajos justifican estrictamente la base teórica de la relación de los autoencoders con la densidad de distribución de los datos de entrenamiento. En los problemas aplicados, a menudo no se requiere un análisis tan serio, por lo tanto, se proporcionará un enfoque ligeramente diferente a continuación que nos permitirá estimar la función de densidad de probabilidad de los datos de entrada debido a un autoencodificador previamente capacitado.

Ejemplo MNIST

Incluso en trabajos anteriores, se propuso la idea empírica de que para el problema de clasificación es posible entrenar codificadores automáticos por el número de clases (enseñando cada una de ellas solo en la submuestra correspondiente). Y elija como respuesta esa clase y codificador automático que brinde la mínima discrepancia entre la imagen de entrada y la reconstruida. No fue difícil verificar en MNIST: entrenar 10 codificadores automáticos (para cada dígito), calcular la precisión y luego comparar con un modelo de varias capas similar del clasificador.

Scripts para entrenamiento y pruebas en git (train_ae.py, calc_codes.py, calc_acc.py)

Arquitectura y número de pesos:



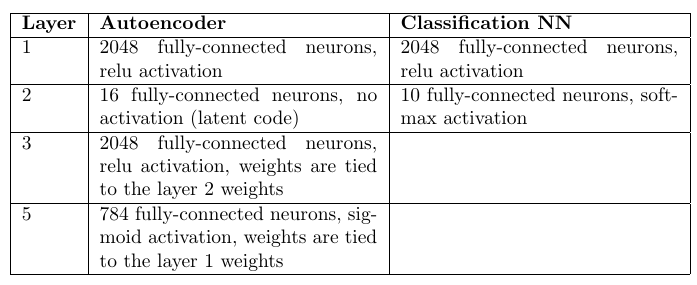
Codificadores automáticos: 98.6%
Clasificador de perceptrón multicapa: 98.4%

Un lector atento notará que había 10 veces más pesos en los codificadores automáticos (por su número). Sin embargo, un aumento de 10 veces en el número de pesos en la capa oculta en un perceptrón multicapa solo empeora las estadísticas.

Por supuesto, las redes de convolución proporcionan una precisión mucho mayor, pero la tarea era solo comparar enfoques, siendo iguales todas las demás cosas.

Como resultado, se puede observar que el enfoque con codificadores automáticos es bastante competitivo con redes totalmente conectadas. Y aunque lleva mucho más tiempo optimizar los pesos, tiene una ventaja importante: la capacidad de detectar anomalías en los datos de entrada. Si ninguno de los codificadores automáticos pudo reconstruir con precisión la imagen de entrada, entonces podemos afirmar que se ingresó una imagen anómala que no ocurrió en la muestra de entrenamiento. Estrictamente hablando, puede reconstruir una imagen no de la muestra de entrada, pero más adelante se mostrará qué hacer en esta situación.

Considere un solo codificador automático

Es posible, de una manera ligeramente diferente que en los documentos anteriores, realizar un análisis cualitativo de la relación entre la densidad de probabilidad de los datos de entrada p (x) y la respuesta del autoencoder.

Codificador automático: uso secuencial de la función del codificador $$$z = g (x)$ y decodificador $$$x ^ * = f (z)$ donde $$$x$ Es el vector de entrada y $$$z$ - rendimiento latente. En algún subconjunto de entrada (generalmente cerca del entrenamiento) $$$x ^ * = x + n = f (g (x))$ donde $$$n$ - discrepancia Aceptamos la discrepancia por el ruido de Gausovsky (sus parámetros se pueden estimar después de entrenar el autoencoder). Como resultado, se hacen una serie de suposiciones bastante fuertes:

1) discrepancia - ruido gaussiano
2) el codificador automático ya está "entrenado" y funciona

Pero, lo que es más importante, casi no se impondrán restricciones al codificador automático.

Además, se puede obtener una estimación cualitativa de la densidad de probabilidad p (x), sobre la base de la cual se pueden hacer varias conclusiones que son muy importantes en el futuro.

Puntuación P (x) para un solo codificador automático

Densidad de distribución para $$$x \ en X$ y $$$z \ en Z$ relacionado de la siguiente manera:

$$

$$p (x) = \ int_ {z} p (x | z) p (z) dz \; \; \; (1)$$

Necesitamos obtener la conexión p (x) y p (z). Para algunos codificadores automáticos, p (z) se establece en la etapa de su entrenamiento; para otros, p (z) es aún más fácil de obtener debido a la menor dimensión Z.

La distribución de densidad del n residual es conocida, lo que significa:

$$

$$p (n) = const \ times exp (- \ frac {(xf (z)) ^ T (xf (z))} {2 \ sigma ^ 2}) = p (x | z) \; \; ( 2)$$

$$$(x-f (z)) ^ T (x-f (z))$ Es la distancia entre x y su proyección x *. En algún punto z * esta distancia alcanzará su mínimo. En este punto, las derivadas parciales del argumento del exponente en la fórmula (2) con respecto a $$$z_i$ (Eje Z) será cero:

$$

$$0 = \ frac {\ partial f (z ^ *)} {\ partial z_i} ^ T (xf (z ^ *)) + (xf (z ^ *)) ^ T \ frac {\ partial f (z ^ * )} {\ parcial z_i}$$

Aqui $$$\ frac {\ partial f (z ^ *)} {\ partial z_i} ^ T (x-f (z ^ *))$ escalar entonces:

$$

$$0 = \ frac {\ partial f (z ^ *)} {\ partial z_i} ^ T (x-f (z ^ *)) \; \; \; (3)$$

La elección del punto z *, donde la distancia $$$(x-f (z)) ^ T (x-f (z))$ mínimo debido al proceso de optimización del codificador automático. Durante el entrenamiento, es el residuo cuadrático el que se minimiza (como regla): $$$\ min \ límites _ {\ theta, \ forall x \ en X train} L2_ {norma} ({x-f_ \ theta (g_ \ theta (x))})$ donde $$$\ theta$ - el peso del codificador. Es decir después del entrenamiento g (x) tiende a z *.

También podemos ampliar $$$f (z)$ en una serie de Taylor (hasta el primer término) alrededor de z *:

$$

$$f (z) = f (z ^ *) + \ nabla f (z ^ *) (z-z ^ *) + o ((z-z ^ *))$$

Entonces, ahora la ecuación (2) se convierte en:

$$

$$p (x | z) \ aprox const \ times exp (- \ frac {((xf (z ^ *)) - \ nabla f (z ^ *) (zz ^ *)) ^ T ((xf (z ^ *)) - \ nabla f (z ^ *) (zz ^ *))} {2 \ sigma ^ 2}) =$$

$$

$$= const \ times exp (- \ frac {(xf (z ^ *)) ^ T (xf (z ^ *))} {2 \ sigma ^ 2}) exp (- \ frac {(\ nabla f (z ^ *) (zz ^ *)) ^ T (\ nabla f (z ^ *) (zz ^ *))} {2 \ sigma ^ 2}) \ times$$

$$

$$\ times exp (- \ frac {(\ nabla f (z ^ *)) ^ T (xf (z ^ *)) + (xf (z ^ *)) ^ T \ nabla f (z ^ *)) (zz ^ *)} {2 \ sigma ^ 2})$$

Tenga en cuenta que el último factor es 1 debido a la expresión (3). El primer factor se puede eliminar mediante el signo de la integral (no contiene z) en (1). Y también suponga que p (z) es una función suficientemente suave y no cambia mucho en la vecindad de z *, es decir reemplace p (z) -> p (z *).

Después de todos los supuestos, la integral (1) tiene la estimación:

$$

$$p (x) = const \ times p (z ^ *) exp (- \ frac {(xf (z ^ *)) ^ T (xf (z ^ *))} {2 \ sigma ^ 2}) \ int_ {z} exp (- (zz ^ *) ^ TW (x) ^ TW (x) (zz ^ *)) dz, \; \; \; z ^ * = g (x)$$

donde $$$W (x) = \ frac {\ nabla f (z ^ *)} {\ sigma}, z ^ * = g (x)$
La última integral es la integral n-dimensional de Euler-Poisson:

$$

$$\ int_ {z} exp (- \ frac {(zz ^ *) ^ TW (x) ^ TW (x) (zz ^ *)} {2}) dz = \ sqrt {\ frac {1} {det ( W (x) ^ TW (x) / 2 \ pi)}}$$

Como resultado, obtuvimos la estimación final p (x):

$$

$$p (x) = const \ times exp (- \ frac {(xf (z ^ * *)) ^ T (xf (z ^ *))} {2 \ sigma ^ 2}) p (z ^ *) \ sqrt {\ frac {1} {det (W (x) ^ TW (x) / 2 \ pi)}}, z ^ * = g (x) \; \; \; (4)$$

Toda esta matemática era necesaria para mostrar que p (x) depende de tres factores:

• La distancia entre el vector de entrada y su reconstrucción, cuanto peor se restaura, menor es p (x)
• Densidades de probabilidad p (z *) en z * = g (x)
• Normalización de la función p (z) en el punto z *, que se calcula para el autoencoder a partir de derivadas parciales de la función f

Y a partir de la constante de normalización, que posteriormente será responsable de la probabilidad a priori de elegir un codificador automático para describir los datos de entrada.

A pesar de todos los supuestos, el resultado fue muy significativo y útil desde el punto de vista de los cálculos.

Clasificación de parámetros o procedimiento de calificación

Ahora puede describir con mayor precisión el procedimiento de clasificación utilizando un conjunto de codificadores automáticos:

1. Entrenamiento de codificadores automáticos independientes para cada clase en la salida correspondiente
2. Cálculo de la matriz W para cada autoencoder
3. Puntuación P (z) para cada codificador automático

Y para cada vector de entrada puede evaluar ahora $$$p (x | clase)$ por la cantidad de clases. Y esta será la función de probabilidad que es necesaria para la toma de decisiones en el marco de la regla bayesiana para la toma de decisiones.

Del mismo modo, los parámetros desconocidos también se pueden estimar dividiendo el espacio de parámetros en valores discretos, entrenando su propio codificador automático para cada valor. Y luego, en función de la mejor puntuación bayesiana, elija el valor que proporcione la función de máxima probabilidad.

Aquí vale la pena señalar que, formalmente, el problema de estimar p (z) no es más simple que estimar p (x). Pero en la práctica esto no es así. El espacio Z generalmente tiene una dimensión mucho más pequeña, o la distribución generalmente se establece al optimizar los pesos del codificador automático.

La idea de combinar el espacio latente de los codificadores automáticos

Hay una curiosa interpretación propuesta por Alexei Redozubov y descrita en los siguientes artículos:

1. Una arquitectura de red neuronal artificial basada en transformaciones de contexto en minicolumnas corticales. Vasily Morzhakov, Alexey Redozubov
2. Memoria holográfica: un nuevo modelo de procesamiento de información por microcircuitos neuronales. Alexey Redozubov, Springer
3. No redes neuronales en absoluto. Morzhakov V.

La información puede tener una interpretación completamente diferente en diferentes contextos. El modelo de un "conjunto de codificadores automáticos" se hace eco de esta idea propuesta. Cualquier codificador automático es un modelo latente de datos de entrada dentro del mismo contexto (una clase u otros parámetros fijos), es decir. el vector latente es una interpretación, y cada codificador automático es un contexto. Al recibir la información de entrada, se considera en cada contexto (por cada codificador automático), y se selecciona el contexto que probablemente tenga en cuenta los modelos existentes en cada codificador automático.

El siguiente paso razonable es permitir la intersección de interpretaciones en diferentes contextos. Es decir Durante el entrenamiento, a menudo sabemos que la interpretación sigue siendo la misma, pero la forma de presentación (contexto) cambia. Por ejemplo, la orientación de un objeto cambia, pero el objeto permanece igual. El vector de la descripción del objeto debe conservarse y el contexto - la orientación cambia.

Luego, si echamos un vistazo a la fórmula (4), el factor p (z) resulta ser estimado para todo el conjunto de codificadores automáticos, y no para cada uno por separado. La interpretación (vector latente) tendrá una distribución común. Para un pequeño número de codificadores automáticos, esto puede no tener un papel importante, pero en una tarea real este número puede ser enorme. Por ejemplo, si define un contexto para cada posible orientación de un objeto 3D, puede haber cientos de miles de ellos. Ahora, cada ejemplo presentado para capacitación en cualquier contexto formará una distribución p (z).

Intercambiabilidad de interpretación y contexto.

En el problema aplicado, surge de inmediato la pregunta: ¿qué asignar por interpretación y qué por contexto? El contexto y la interpretación pueden intercambiarse fácilmente, y nadie excluye la posibilidad del funcionamiento simultáneo en paralelo de un par de "conjuntos de autoencoders".

Para mayor claridad, puede ofrecer este ejemplo:

La imagen de entrada contiene los rostros de las personas.

1. contexto - orientación de la cara. Luego, para la reconstrucción de la imagen de entrada, no tenemos suficiente "interpretación": un código que identifique a una persona, que contendrá una descripción de la cara, el peinado y su iluminación. Durante el entrenamiento, tendremos que presentar la misma cara desde diferentes lados, "congelando" el código latente, mientras se cambia la orientación.
2. contexto: tipo de cara, iluminación, peinado. Luego, para la reconstrucción de la imagen de entrada, nos falta la orientación de la cara. Durante el entrenamiento, será necesario mostrar diferentes caras en diferentes condiciones de iluminación, pero con la misma orientación.

La decisión bayesiana óptima en el primer caso se tomará con respecto a la orientación de la cara, y en el segundo, su tipo. Presumiblemente, la primera opción dará una mejor precisión en la orientación, y la segunda evaluará con mayor precisión de quién era la cara.

Aprender un conjunto de codificadores automáticos con espacio latente compartido

En el entrenamiento, necesitamos saber cómo se ve una entidad en términos de significado en diferentes contextos. Por ejemplo, si hablamos de la imagen de los números y la orientación contextual, entonces esquemáticamente dicho entrenamiento cruzado se ve así:



Se utiliza el codificador de un codificador automático, luego el decodificador de otro codificador automático decodifica el código latente. La función de pérdida de aprendizaje sigue siendo estándar. Es interesante que si el codificador automático se selecciona simétrico (es decir, los pesos del codificador y el decodificador están conectados), en cada iteración se optimizan todos los pesos de ambos codificadores automáticos.

El más conveniente para un entrenamiento tan complicado fue PyTorch, que le permite crear esquemas bastante complejos para la propagación inversa de errores, incluidos los dinámicos.

Los pasos de aprendizaje estándar de cada codificador automático se alternan con la iteración del entrenamiento cruzado. Como resultado, todos los codificadores automáticos tienen un espacio latente común o "interpretación" en diferentes contextos.

Es muy importante que, como resultado de dicho análisis, podamos dividir la información de entrada en "contexto" e "interpretación".

Ejemplo de entrenamiento

Considere un ejemplo bastante simple basado en MNIST, que ayudará a demostrar el principio de entrenar codificadores automáticos con un espacio latente común. Como resultado, este ejemplo demostrará la formación del concepto abstracto de "cubo" utilizando el mecanismo descrito en el artículo.

Los números de MNIST se trazan en el borde del cubo y gira alrededor de uno de sus ejes:



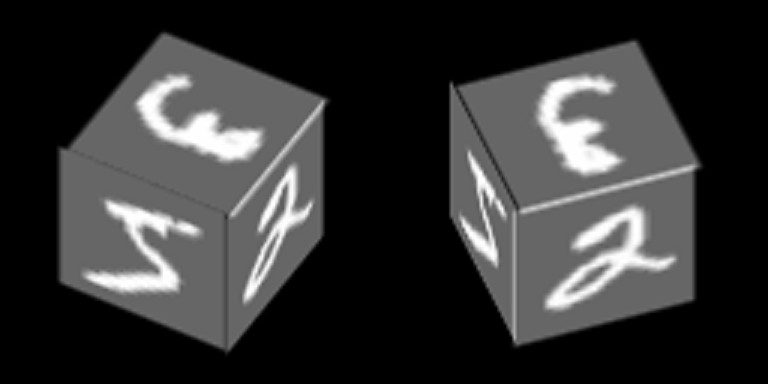
Entrenaremos codificadores automáticos para restaurar caras, orientación de contexto - cara.

Aquí hay un ejemplo del número "cero" en 100 contextos, los primeros 34 de los cuales corresponden a diferentes ángulos de rotación de la cara lateral, y los 76 restantes - diferentes ángulos de rotación del lado superior.



Suponemos que para cada una de estas 100 imágenes las "interpretaciones" deberían ser las mismas, y son sus combinaciones aleatorias las que se utilizan para el entrenamiento cruzado.

Después de entrenar con el método descrito anteriormente, fue posible lograr que el código latente de uno de los autoencoders pueda ser decodificado por otros autoencoders, obteniendo una conversión contextual realmente significativa.

Por ejemplo, esta imagen muestra cómo el resultado de codificación del codificador automático en el número 10 es decodificado por otros codificadores automáticos para uno de los dígitos:



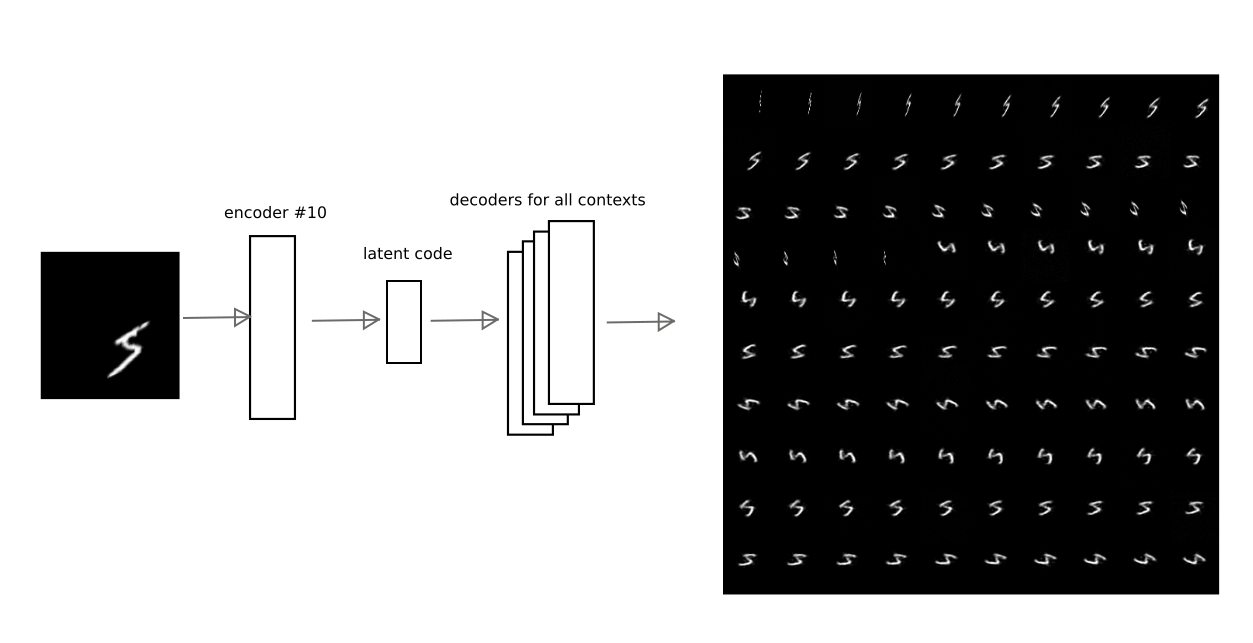
Por lo tanto, tener el código de "interpretación", es decir vector latente del codificador automático, puede restaurar la imagen original en cualquiera de los contextos entrenados (es decir, el decodificador de cualquier codificador automático).

Entrada de enmascaramiento vectorial

En la fórmula (4), la dispersión del residuo $$$\ sigma$ , que se elige mediante una constante para cualquiera de los componentes del vector de entrada. Sin embargo, si algunos componentes no tienen ninguna relación estadística con el modelo latente, entonces la varianza probablemente será significativamente mayor para estos componentes. La dispersión está en todas partes en el denominador, lo que significa que cuanto mayor es la discrepancia, menor es la contribución del error del componente. Puede relacionarse con esto como un enmascaramiento de alguna parte del vector de entrada.

Para este ejemplo con caras giratorias, la máscara es obvia: la proyección de la cara en un contexto específico.



En el enfoque simplificado de este ejemplo, que usa solo el residuo entre la imagen de entrada y la reconstrucción, solo necesita multiplicar el residuo por la máscara para cada uno de los contextos.

En el caso general, es necesario evaluar más estrictamente los parámetros de distribución, sin ingresar manualmente la máscara.

Separación de la interpretación del contexto.

Separando la interpretación del contexto, puede obtener conceptos abstractos. En el ejemplo entrenado, es interesante demostrar 2 efectos:

1) aprendizaje único, es decir entrenamiento con un número extremadamente pequeño de ejemplos (en el límite de uno).

Si analizamos solo la interpretación, ignorando el contexto, entonces es posible reconocer una nueva imagen en diferentes orientaciones faciales, cuando se muestra una nueva imagen en solo una de las orientaciones.

Es importante tener en cuenta que se debe presentar una nueva imagen. En aras de la corrección, también nos propusimos el objetivo de recordar no una imagen, sino aprender a compartir 2 nuevas imágenes que no se encontraban previamente en la base de capacitación MNIST. Por ejemplo, tales:



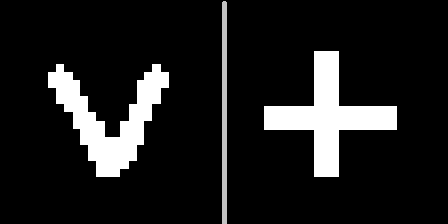La idea es la siguiente: muestre estos signos en uno de los contextos geométricos (por ejemplo, bajo el número 10), seleccione un hiperplano que se extienda equidistante de las interpretaciones de estos signos y luego asegúrese de que con este hiperplano podamos reconocer qué tipo de signo se nos presenta cuando se gira la cara (otros contextos)

Es importante tener en cuenta que los codificadores automáticos no recibirán capacitación sobre nuevos signos. Debido a la variedad de números que hay en MNIST, puede predecir cómo se verá un nuevo personaje que no se haya visto antes en diferentes contextos.

Dado que el signo se verá como después V codificación y decodificación de contexto №10 restante en:



Se puede observar que la predicción no es perfecto, pero visualmente reconocible.

Denotamos esta demostración como "experimento 1" y describimos el resultado a continuación.

2) y con el cubo es interesante demostrar lo que sucederá si ignora el contenido del vector latente, y solo se transmite el grado de plausibilidad de cada codificador automático.

Veamos cómo es la probabilidad para cada uno de los contextos para dos cubos con texturas completamente diferentes (números 5 y 9) para 100 contextos que se pueden mostrar como un mapa:



se puede ver que los mapas son bastante similares, a pesar de la diferente textura en los lados del cubo.

Es decirEl vector en sí, que contiene la probabilidad de modelos de autoencoder (contextos), nos permite formular un nuevo concepto abstracto relacionado con la forma tridimensional de un cubo. Este vector también se puede describir en el siguiente nivel mediante un codificador automático que aprende el modelo de cubo.

En el segundo experimento, será necesario crear un segundo nivel de procesamiento de información en el que entrenar el codificador automático de un modelo de cubo abstracto. Y luego, usando la proyección posterior para restaurar la imagen original para diferentes implementaciones del modelo de este cubo. En pocas palabras, haz girar el cubo.

El resultado del "experimento número 1"

El conjunto de codificadores automáticos entrenados por MNIST se aplica a dos nuevas imágenes presentadas en el contexto # 10. Resulta 2 puntos en el espacio latente correspondiente a los signos de V y +. Definimos un plano equidistante de ambos puntos, que usaremos para tomar una decisión. Si el punto está en un lado del avión, el signo V, en el otro, el signo más.

Ahora obtenemos los códigos de las imágenes convertidas y para cada una de ellas calculamos la distancia al avión, conservando el signo.

Como resultado, es posible distinguir qué tipo de signo se presentó para los 100 contextos.

Distribución de distancias en el gráfico:



visualización del resultado utilizando símbolos individuales como ejemplo:



Es decirLos códigos latentes de signos V en contextos completamente diferentes están mucho más cerca uno del otro en el espacio latente que V y los códigos de signo más en el mismo contexto. Debido a esto, en 100 de cada 100 casos, es posible distinguir con éxito los signos en varias orientaciones de las caras del cubo, a pesar de que solo se presentó una muestra de cada signo.

Fue posible demostrar el clásico "aprendizaje único", que es imposible en la arquitectura original de las redes neuronales artificiales. El principio básico por el cual funciona este enfoque es muy similar al "aprendizaje de transferencia" demostrado, por ejemplo, en este artículo .

Referencia a git (train_ae_shared.py, test_AB.py)

El resultado del "experimento número 2"

Separar las interpretaciones del contexto también permite aprender de un conjunto limitado de ejemplos. Es posible demostrar solo una de las posibles interpretaciones en varios contextos (fijar un "vector latente"). Se puede obtener un modelo de cubo abstracto con solo mostrar un dígito en todas las caras.

El experimento está estructurado de la siguiente manera:

1. Se está preparando una base de entrenamiento: cubos con un grado de rotación de 0 a 90 grados. En las caras de los cubos está el número 5.
2. El vector de probabilidad de contextos, separado de la interpretación (código latente), se pasa al siguiente nivel, donde se capacita al codificador automático responsable del modelo de cubo.
3. : , «», , , , , .

La muestra de entrenamiento consistió en 5421 imágenes con la imagen del número 5 en los lados, por ejemplo:


cubos con rotación de 0 a 90 grados

. Sabemos de antemano que el cubo tiene solo un grado de libertad de rotación, por lo tanto, el codificador automático en el segundo nivel tiene solo un componente en el código latente. Después de la formación pueden variar este componente es de 0 a 1 (activación de la función de la capa latente fue seleccionado sigmoide) y ver lo que reproducen contextos vector de probabilidad cuando se decodifica:



Este vector se transmite entonces al nivel 1, en el que 100 contextos caras orientaciones se seleccionan máximos locales y ' imaginó "cualquier código latente del signo en las caras del cubo. "Imagine" el número 3 en las caras, cambiando el vector latente en el codificador automático responsable del concepto abstracto de un cubo, y obtenga la siguiente imagen de un cubo:



O el código del signo V, que no se encontró en absoluto en el conjunto de entrenamiento:



la calidad es peor, pero el signo es reconocible.

Por lo tanto, en el segundo nivel de procesamiento de imágenes, obtuvimos un codificador automático que modela la variedad del concepto abstracto de "cubo". En la práctica, en problemas de reconocimiento, el principio de retroproyección mostrado en el experimento es extremadamente importante, porque permite eliminar las ambigüedades de interpretación debido a la formación de conceptos abstractos de un nivel superior.

Referencia a git (second_level.py, second_level_test.py)

Otros ejemplos donde funciona la separación de contexto

En mi artículo anterior, al reconocer los números de automóviles, se utilizó un método similar sin explicación. La posición, orientación y escala de los números en la imagen se separaron de los contenidos, el siguiente nivel percibió estos datos para construir el modelo de "número de automóvil". No importa qué números, su configuración geométrica mutua es importante, por lo que podemos decir con confianza que este es un número de automóvil (por cierto, también un concepto abstracto).

Por analogía, podemos dar otros ejemplos de la visión por computadora: la forma 3D de un objeto o sus contornos son separables de su textura y fondo; La enumeración de los componentes aisladamente de la configuración espacial mutua también a menudo permite la formación de un nuevo concepto abstracto.

También es interesante cómo esto puede funcionar en otras áreas del aprendizaje automático: resaltar la melodía de una canción también es negarse a interpretar (qué vocal se pronuncia) y usar solo el contexto (tono); construcciones gramaticales (patrones, por ejemplo, "alguien hizo algo").

Discusión del problema de la IA fuerte

Por el momento, es difícil formular cómo la IA fuerte difiere de la débil. Probablemente, esta lista debe incluir todo lo que falta en los enfoques y algoritmos existentes para que las computadoras actúen de manera tan eficiente como una persona, por ejemplo:

• Tomar decisiones, usar estrategias, resolver frente a la incertidumbre. Es una gran incertidumbre lo que requiere elegir el mejor de los modelos formulados durante el entrenamiento.
• Reflexión de modelos del mundo físico y social circundante, incluida la autoconciencia y la conciencia de los demás.
• Los mecanismos del pensamiento abstracto, que permiten formular conceptos que pueden utilizarse posteriormente en una amplia variedad de datos de entrada.
• Capacidad para "descifrar" tus propios pensamientos

Además, claramente no hay suficientes mecanismos de memoria desarrollados integrados con el proceso de aprendizaje, mecanismos de promoción / castigo.

El artículo demuestra el enfoque del problema de reconocimiento y estimación de parámetros, que se basa en la selección del mejor modelo que describe los datos de entrada. Se supone que este es el mecanismo para elegir la mejor interpretación y contexto. Debido a la separación de la interpretación y el contexto en la salida del módulo (un conjunto de codificadores automáticos), se pueden formular conceptos abstractos o generalizar la experiencia aislada del contexto, reduciendo así la muestra de entrenamiento. Los conjuntos de contextos pueden reflejar las lecturas de los sensores de la máquina (orientación, posición, velocidad, etc.), debido a lo cual es posible el aprendizaje natural sin un maestro.

Además, aunque el aprendizaje profundo se utiliza en la formación de autoencoders, los procesos que ocurren en los autoencoders se analizan fácilmente en cada nivel de procesamiento de información, porque Es posible determinar en qué modelo (o en qué contexto) se encontró la mejor interpretación. Y el significado de las retroalimentaciones entre los niveles que deben introducirse en sistemas complejos es aumentar o disminuir la probabilidad de elegir un contexto particular.

Resultado

Se propone un aparato matemático, en base al cual se puede elegir uno u otro modelo que describa los datos de entrada, guiados por la regla de decisión bayesiana. Los modelos se obtienen utilizando autoencoders con un espacio latente común. Se propone una idea según la cual el código latente del codificador automático es una interpretación, y el modelo latente, es decir, El codificador automático en sí mismo es el contexto.

Está demostrado que el conjunto de codificadores automáticos no es inferior en precisión a las redes neuronales artificiales completamente conectadas utilizando el ejemplo de MNIST.

Se muestra el efecto de separar la interpretación del contexto: minimización del conjunto de datos necesarios (en el límite de "aprendizaje de una sola vez") para el reconocimiento de imágenes recién presentadas debido al entrenamiento previo en otros datos.

Se muestra el efecto de separar el contexto de la interpretación: la posibilidad de formar conceptos abstractos del siguiente nivel utilizando el "cubo" de abstracción geométrica como ejemplo.

Referencias

1) Alain, G. y Bengio, Y. Lo que los autoencoders regularizados aprenden de la distribución de generación de datos. 2013
2) Kamyshanska, H. 2013. Sobre la puntuación del autoencoder
3) Daniel Jiwoong Im, Mohamed Ishmael Belghazi, Roland Memisevic. 2016. Conservación de los codificadores automáticos desatados
4) Una arquitectura de red neuronal artificial basada en transformaciones de contexto en minicolumnas corticales. Vasily Morzhakov, Alexey Redozubov
5) Memoria holográfica: un modelo novedoso de procesamiento de información por microcircuitos neuronales. Alexey Redozubov, Springer
6) No redes neuronales en absoluto. Morzhakov V.
7) en.wikipedia.org/wiki/Gaussian_integral
8) Ejemplos adversarios: ataques y defensas para el aprendizaje profundo
9) Aprendizaje de imitación de un disparo

PD: Este artículo es una preimpresión electrónica en ruso, publicada para analizar los resultados y buscar errores. ¡Cualquier crítica constructiva es bienvenida!