
Las propiedades de los números primos rara vez le permiten trabajar con ellos de manera diferente que en forma de una matriz precalculada, y preferiblemente lo más voluminoso posible. El formato de almacenamiento natural en forma de enteros de una u otra capacidad de dígitos sufre al mismo tiempo algunas desventajas que se vuelven significativas con el crecimiento del volumen de datos.
Entonces, el formato de enteros sin signo de 16 bits con el tamaño de una tabla de este tipo es de aproximadamente 13 kilobytes, contiene solo 6542 primos: seguido del número 65531 son los valores de mayor profundidad de bits. Tal mesa es adecuada solo como un juguete.
El formato entero más popular de 32 bits en la programación parece mucho más sólido: le permite almacenar alrededor de 203 millones de simples. Pero esa mesa ya ocupa unos 775 megabytes.
El formato de 64 bits tiene aún más perspectivas. Sin embargo, con una potencia teórica del orden de los valores 1e + 19, la tabla tendría un tamaño de 64 exabytes.
Realmente no se cree que nuestra humanidad progresiva alguna vez en el futuro previsible calcule una tabla de números primos de tal volumen. Y el punto aquí no es tanto en volúmenes como en el tiempo de conteo de los algoritmos disponibles. Digamos, si la tabla de todos los simples de 32 bits todavía se puede calcular de forma independiente en unas pocas horas (Fig. 1), entonces para la tabla al menos un orden de magnitud mayor tomará varios días. Pero tales volúmenes hoy: este es solo el nivel inicial.
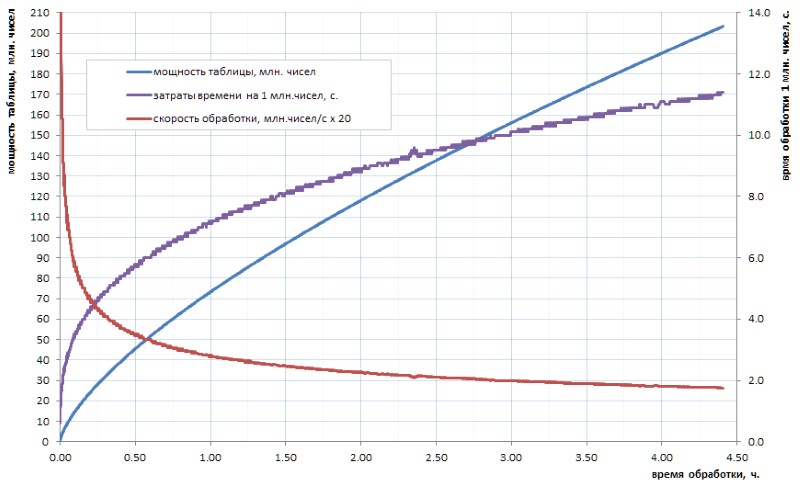
Como se puede ver en el diagrama, el tiempo de cálculo específico después del tirón inicial pasa suavemente al crecimiento asintótico. El es bastante lento. pero esto es crecimiento, lo que significa que extraer cada siguiente dato a lo largo del tiempo será cada vez más difícil. Si desea hacer un avance significativo, tendrá que paralelizar el trabajo a través de los núcleos (y se paraleliza bien) y colgarlo en las supercomputadoras. Con la perspectiva de obtener los primeros 10 mil millones simples en una semana, y 100 mil millones, solo en un año. Por supuesto, hay algoritmos más rápidos para el cálculo simple que el busto trivial utilizado en mi tarea, pero, en esencia, esto no cambia el asunto: después de dos o tres órdenes de magnitud, la situación se vuelve similar.
Por lo tanto, sería bueno haber realizado el trabajo de conteo una vez, almacenar su resultado en una forma tabular lista para usar y usarlo según sea necesario.
Debido a lo obvio de la idea, la red se encuentra con muchos enlaces a listas preparadas de primos ya calculados por alguien. Por desgracia, en la mayoría de los casos solo son adecuados para manualidades de los estudiantes: uno de ellos, por ejemplo, va de un sitio a otro e incluye 50 millones de simples. Esta cantidad solo puede sorprender a los no iniciados: ya se mencionó anteriormente que en una computadora doméstica en unas pocas horas puede calcular de forma independiente la tabla de todas las simples de 32 bits, y es cuatro veces más grande. Probablemente hace unos 15-20 años, tal lista fue de hecho un logro heroico para la comunidad laica. Hoy, en la era de los dispositivos multi-core multi-gigahercios y multi-gigabytes, esto ya no es impresionante.
Tuve la suerte de familiarizarme con el acceso a una tabla mucho más representativa de las simples, que utilizaré más como ilustración y sacrificio para mis experimentos de campo. Con el propósito de conspirar, la llamaré 1TPrimo . Contiene todos los números primos menos de un billón.
Usando 1TPrimo como ejemplo, es fácil ver con qué volúmenes tiene que lidiar. Con una capacidad de alrededor de 37,6 mil millones de valores en formato entero de 64 bits, esta lista es de 280 gigabytes. Por cierto, esa parte que podría caber en 32 dígitos representa solo el 0.5% del número de números representados en él. Esto deja absolutamente claro que cualquier trabajo serio con primos inevitablemente tiende a una profundidad total de 64 bits (o más).
Por lo tanto, la tendencia sombría es obvia: una tabla seria de números primos inevitablemente tiene un volumen titánico. Y de alguna manera debemos luchar contra esto.
Lo primero que viene a la mente al mirar una tabla (Fig. 2) es que consiste en valores consecutivos casi idénticos que difieren solo en uno o dos de los últimos lugares decimales:
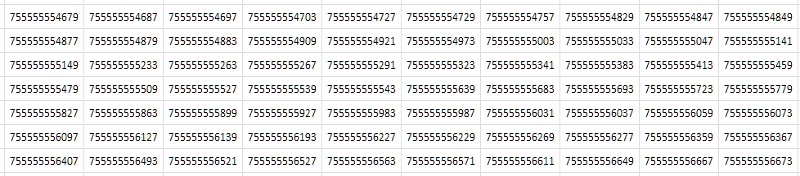
Simplemente, a partir de las consideraciones abstractas más generales: si el archivo tiene muchos datos duplicados, entonces el archivador debería comprimirlo bien. De hecho, la compresión de la tabla 1TPrimo con la popular utilidad 7-zip en configuraciones estándar dio una relación de compresión bastante alta: 8.5. Es cierto que el tiempo de procesamiento, con el gran tamaño de la tabla de origen, en un servidor de 8 núcleos, con una carga promedio de todos los núcleos de aproximadamente 80-90%, fue de 14 horas 12 minutos. Los algoritmos de compresión universal están diseñados para algunas ideas abstractas y generalizadas sobre datos. En algunos casos especiales, los algoritmos de compresión especializados basados en las características conocidas del conjunto de datos entrantes pueden demostrar indicadores mucho más efectivos, a los que se dedica este trabajo. Y cuán efectivo se volverá claro a continuación.
Los valores numéricos cercanos de los números primos vecinos requieren una decisión de no almacenar estos valores por sí mismos, sino los intervalos (diferencias) entre ellos. En este caso, se pueden lograr ahorros significativos debido al hecho de que la profundidad de bits de los intervalos es mucho menor que la profundidad de bits de los datos iniciales (Fig. 3).
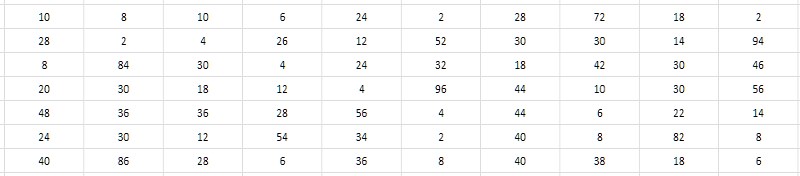
Y parece que no depende de la profundidad de bits de los simples que generan el intervalo. Una búsqueda exhaustiva muestra que los valores típicos de intervalos para primos tomados de varios lugares en la tabla 1TPrimo se encuentran dentro de unidades, decenas, a veces cientos y, como la primera oración de trabajo, probablemente podrían caber en el rango de 8 bits enteros sin signo, es decir, bytes. Sería muy conveniente, y en comparación con el formato de 64 bits, esto conduciría inmediatamente a una compresión de datos de 8 veces, justo en algún lugar al nivel demostrado por el archivador de 7 zip. Además, la simplicidad de los algoritmos de compresión y descompresión debería tener, en principio, un gran impacto en la velocidad de compresión y acceso a los datos en comparación con 7-zip. Suena tentador
Está absolutamente claro que los datos convertidos de sus valores absolutos a los intervalos relativos entre ellos son adecuados solo para restaurar una serie de valores que vienen en una fila desde el comienzo de la tabla principal. Pero si agregamos una estructura mínima de índice de bloque a dicha tabla de intervalos, entonces con costos indirectos adicionales insignificantes, esto nos permitirá restaurar, pero ya bloque por bloque, tanto el elemento de la tabla por su número y el elemento más cercano por un valor establecido arbitrariamente, y estas operaciones, junto con la operación principal muestras de secuencia: en general, agota la mayor parte de las posibles consultas a dichos datos. El procesamiento estadístico, por supuesto, se volverá más complicado, pero seguirá siendo bastante transparente, ya que no hay ningún truco en particular para recuperarlo "sobre la marcha" de los intervalos disponibles al acceder al bloque de datos requerido.
Pero por desgracia. Un experimento numérico simple en datos de 1TPrimo muestra que ya al final de las terceras decenas de millones (esto es menos de una centésima parte del volumen de 1TPrimo), y en cualquier otro lugar, los intervalos entre primos vecinos regularmente van más allá del rango de 0..255.
Sin embargo, un experimento numérico ligeramente complicado revela que el crecimiento del intervalo máximo entre primos vecinos con el crecimiento de la tabla en sí es muy, muy lento, lo que significa que la idea sigue siendo buena de alguna manera.
La segunda mirada más cercana a la tabla de intervalos sugiere que es posible almacenar no la diferencia en sí, sino su mitad. Como todos los números primos mayores que 2 son obviamente impares, respectivamente, sus diferencias son obviamente pares. En consecuencia, las diferencias pueden reducirse en 2 sin pérdida de valor; y para completar, también se puede restar uno del cociente obtenido para usar de manera útil el valor cero que no se reivindica de otra manera (Fig. 4). Tal reducción de intervalos se denominará en adelante monolítica, en contraste con la forma inicial porosa y suelta, en la que todos los valores impares y cero resultaron no reclamados.
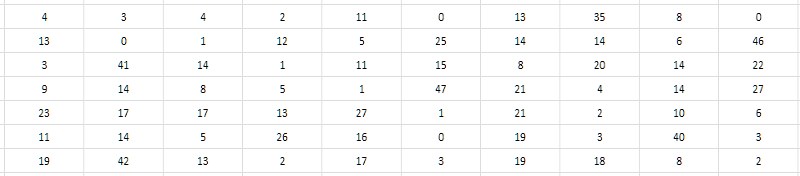
Cabe señalar que dado que el intervalo entre los dos primeros simples (2 y 3) no encaja en este esquema, entonces 2 deberá excluirse de la tabla de intervalos y tener este hecho en mente todo el tiempo.
Esta técnica simple le permite codificar intervalos de 2 a 512 en el rango de valores 0..255. Una vez más, la esperanza se hace realidad de que el método de diferencia nos permitirá empacar una secuencia de primos mucho más poderosa. Y con razón: una serie de 37,6 mil millones de valores presentados en la lista 1TPrimo reveló solo 6 (¡seis!) Intervalos que no están en el rango de 2..512.
Pero eso fue una buena noticia; Lo malo es que estos seis intervalos se encuentran dispersos en la lista con bastante libertad, y el primero de ellos ocurre ya al final del primer tercio de la lista, lo que convierte los dos tercios restantes en lastre inadecuado para este método de compresión (Fig. 5):
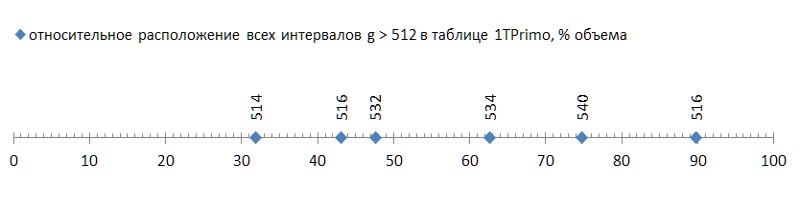
Tal rubor (¡unas desafortunadas seis piezas por casi cuarenta mil millones! - y en ti ...) incluso con una mosca en la pomada para comparar - para mostrar el honor del alquitrán. Pero, por desgracia, este es un patrón, no un accidente. Si rastreamos la primera aparición de intervalos entre números primos según la longitud de los datos, queda claro que este fenómeno radica en la genética de los números primos, aunque progresa extremadamente lentamente (Fig. 6 *).
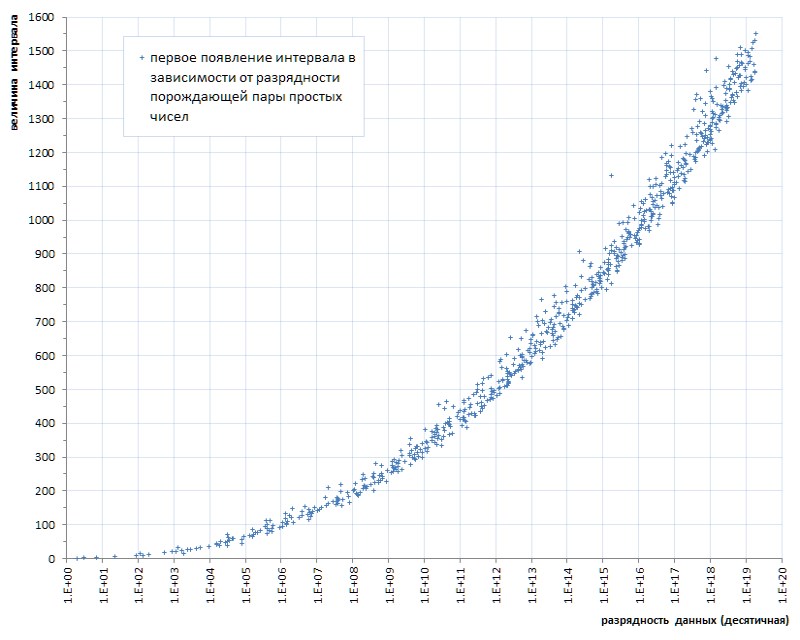
* Calendario compilado según el sitio temático de Thomas R. Nisley ,
que son varios órdenes de magnitud superiores al poder de la lista 1TPrimo
Pero incluso este progreso muy lento sugiere inequívocamente: uno puede limitarse a una determinada profundidad de bits predeterminada de un intervalo solo a una determinada potencia predeterminada de la lista. Es decir, no es adecuado como solución universal.
Sin embargo, el hecho de que el método propuesto para comprimir una secuencia de números primos le permite implementar una tabla compacta simple con una capacidad de casi 12 mil millones de valores ya es un resultado. Dicha tabla ocupa un volumen de 11,1 gigabytes, frente a 89,4 gigabytes en un formato trivial de 64 bits. Seguramente para una serie de aplicaciones, tal solución puede ser suficiente.
Y lo que es interesante: el procedimiento para traducir una tabla 1TPrimo de 64 bits al formato de intervalos de 8 bits con una estructura de bloques, utilizando solo un núcleo de procesador (para la paralelización, tendría que recurrir a una complicación significativa del programa, y no valió la pena) y no más de 5 El% de la carga del procesador (la mayor parte del tiempo dedicado a las operaciones de archivo) tomó solo 19 minutos Contra, recuerdo, 14 horas en ocho núcleos al 80-90% de la carga gastada por el archivador 7-zip.
Por supuesto, solo el primer tercio de la tabla se sometió a esta traducción, en la que el rango de intervalos no excede de 512. Por lo tanto, si lleva las 14 horas completas al mismo tercio, entonces se deben comparar 19 minutos con casi 5 horas del archivador de 7 zip. Con una cantidad comparable de compresión (8 y 8.5), la diferencia es de aproximadamente 15 veces. Teniendo en cuenta que la mayor parte del tiempo de trabajo del programa de transmisión estaba ocupado por operaciones de archivos, la diferencia sería aún mayor en un sistema de disco más rápido. E intelectualmente, el tiempo de funcionamiento de 7-zip en ocho núcleos aún debe contarse en un hilo, y luego la comparación será realmente adecuada.
La selección de dicha base de datos difiere muy poco en el tiempo de la selección de la tabla de datos desempaquetados y está determinada casi por completo por el tiempo de las operaciones de archivo. Los números específicos dependen en gran medida del hardware específico, en mi servidor, en promedio, el acceso a un bloque de datos arbitrario tomó 37.8 μs, mientras que la lectura secuencial de bloques - 4.2 μs por bloque, para el desempaquetado completo del bloque - menos de 1 μs. Es decir, no tiene sentido comparar la descompresión de datos con el trabajo de un archivador estándar. Y esta es una gran ventaja.
Y, finalmente, las observaciones ofrecen otra tercera solución que elimina cualquier restricción sobre el poder de los datos: codificación de intervalos con valores de longitud variable. Esta técnica ha sido ampliamente utilizada en aplicaciones relacionadas con la compresión. Su significado es que si se encuentra en la entrada que a menudo se encuentran algunos valores, algunos son menos comunes y otros son muy raros, entonces podemos codificar el primero con códigos cortos, el segundo con códigos más auténticos y el tercero - muy largo (tal vez incluso muy largo, porque no importa: de todos modos, estos datos son muy raros). Como resultado, la longitud total de los códigos recibidos puede ser mucho más corta que los datos de entrada.
Ya observando el gráfico de la aparición de los intervalos en la figura 7, podemos suponer que si los intervalos son 2, 4, 6, etc. aparecen antes de los intervalos, digamos, 100, 102, 104, etc., entonces el primero debería continuar ocurriendo con mucha más frecuencia que el segundo. Y viceversa, si los intervalos 514 se encuentran solo a partir de 11.99 mil millones, 516 - a partir de 16.2 mil millones y 518 - generalmente a partir de solo 87.7 mil millones, entonces se encontrarán muy raramente. Es decir, a priori, podemos asumir la relación inversa entre el tamaño del intervalo y su frecuencia en una secuencia de números primos. Y eso significa que puede construir una estructura simple que implemente códigos de longitud variable para ellos.
Por supuesto, las estadísticas sobre la frecuencia de los intervalos deberían ser determinantes para la elección de un método de codificación particular. Afortunadamente, en contraste con los datos arbitrarios, la frecuencia de los intervalos entre los números primos, que en sí mismos son una secuencia estrictamente determinada, de una vez por todas, también es una característica estrictamente determinada, de una vez por todas.
La Figura 7 muestra la respuesta de frecuencia de los intervalos para toda la lista 1TPrimo:
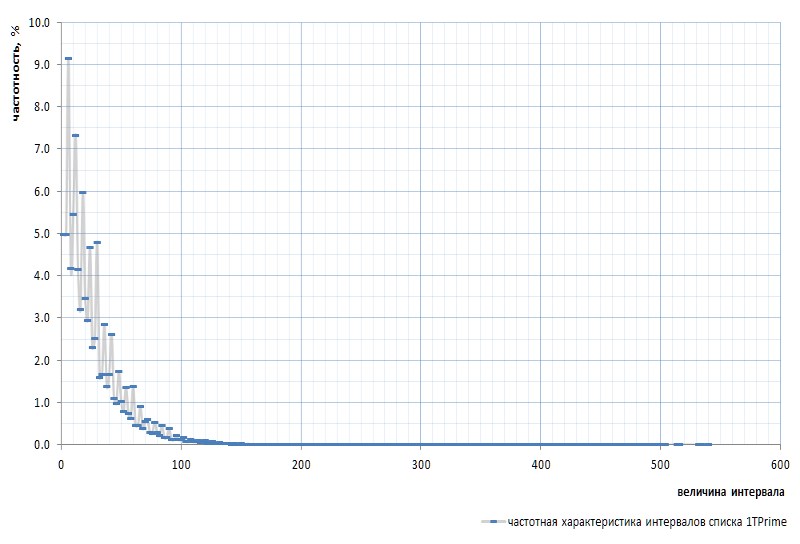
Aquí es necesario mencionar nuevamente que el intervalo entre los primeros primos 2 y 3 está excluido del gráfico: este intervalo es 1 y ocurre exactamente una vez en la secuencia de primos, independientemente de la potencia de la lista. Este intervalo es tan peculiar que es más fácil eliminar 2 de la lista de simples que desviarse constantemente a las reservas. El sim se declara que el número 2 es primo virtual : no está visible en las listas, pero está allí. Como esa gopher.
A primera vista, el gráfico de frecuencia confirma completamente la suposición a priori dada por un par de párrafos anteriores. Muestra claramente la heterogeneidad estadística de los intervalos y la alta frecuencia de valores pequeños en comparación con los grandes. Sin embargo, en la segunda vista, más convexa, el gráfico resulta ser mucho más interesante (Fig. 8):
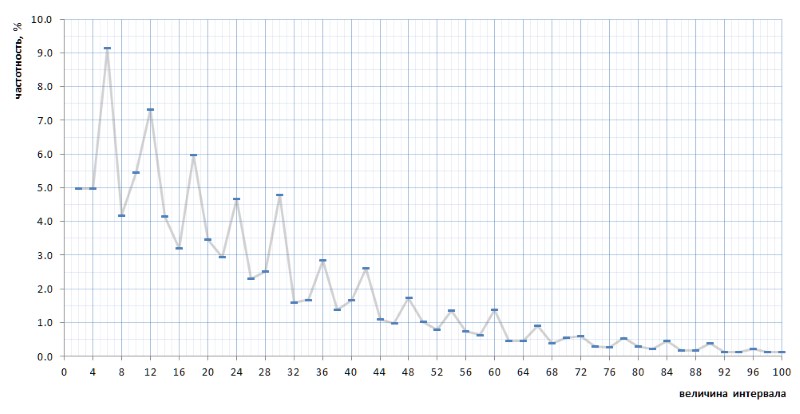
Muy inesperadamente, resulta que los intervalos más frecuentes no son 2 y 4, como parece ser por consideraciones generales, sino 6, 12 y 18, seguidos por 10, y solo entonces 2 y 4 con una frecuencia casi igual (diferencia en 7 dígitos) después del punto decimal). Y además, la multiplicidad de valores máximos del número 6 se traza en todo el gráfico.
Aún más interesante, esta naturaleza inadvertidamente revelada del gráfico es universal, y, en todos los detalles, con todas sus torceduras, en toda la secuencia de intervalos simples representados por la lista 1TPrimo, es probable que sea universal para cualquier secuencia de intervalos simples (por supuesto, una declaración tan audaz necesita prueba, que con mucho gusto transfiero a los hombros de especialistas en teoría de números). La Figura 10 muestra una comparación de las estadísticas de intervalo completo (línea escarlata) con muestras de intervalo limitado tomadas en varios lugares arbitrarios en la lista 1TPrimo (líneas de otros colores):
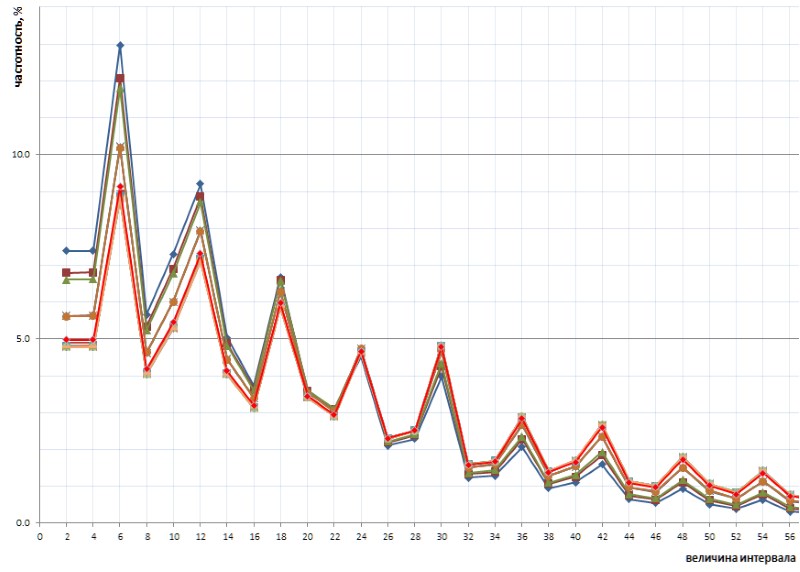
Se puede ver en este gráfico que todas estas muestras se repiten exactamente, con solo una ligera diferencia en las partes izquierda y derecha de la figura: parecen estar ligeramente giradas en sentido contrario a las agujas del reloj alrededor del punto de intervalo con un valor de 24. Esta rotación probablemente se deba al hecho de que la más alta en la izquierda partes de los gráficos se basan en muestras con profundidades de bits más bajas. En tales muestras, todavía no existen, o son raros los intervalos grandes, que se vuelven frecuentes en muestras con profundidades de bits más altas. En consecuencia, su ausencia está a favor de la frecuencia de los intervalos con valores más bajos. En muestras con profundidades de bits más altas, aparecen muchos intervalos nuevos con valores grandes; por lo tanto, la frecuencia de intervalos más pequeños disminuye ligeramente. Lo más probable es que el punto de pivote, con un aumento en el poder de la lista, cambie hacia valores más grandes. En algún lugar, al lado, está el punto de equilibrio de la gráfica, donde la suma de todos los valores de la derecha es aproximadamente igual a la suma de todos los valores de la izquierda.
Esta naturaleza interesante de la frecuencia de los intervalos sugiere abandonar la estructura trivial de los códigos de longitud variable. Típicamente, dicha estructura consiste en un paquete de bits de varias longitudes y propósitos. Por ejemplo, primero viene un cierto número de bits de prefijo establecidos en un valor específico, por ejemplo, 0. Hay un bit de detención detrás de ellos, que debe indicar la finalización del prefijo y, en consecuencia, debe diferir del prefijo: 1 en este caso. El prefijo puede no tener ninguna longitud, es decir, una y otra vez, el muestreo puede comenzar inmediatamente con un bit de parada, determinando así la secuencia más corta. El bit de detención suele ir seguido de un sufijo, cuya longitud está determinada de alguna manera predeterminada por la longitud del prefijo. , , — . , - . - (, , - ) , .
, .
Y aquí debería mencionarse una cosa más importante. A primera vista, la ciclicidad observada implica la división de los intervalos en triples: {2,4, 6 } , {8,10, 12 } , {14,16, 18 } y así sucesivamente (los valores con la frecuencia máxima en cada triple están marcados en negrita) . Sin embargo, de hecho, el ciclo aquí es ligeramente diferente.
No citaré toda la línea de razonamiento, que, de hecho, no existe: era una suposición intuitiva, complementada por un método de enumeración contundente de opciones, cálculos y muestras que tomó varios días de forma intermitente. La ciclicidad revelada como resultado consiste en seis intervalos {2,4, 6 ,8,10, 12 } , {14,16, 18 ,20,22, 24 } , {26,28, 30 ,32,34, 36 } y etc. (los intervalos de frecuencia máxima se resaltan nuevamente en negrita).
En pocas palabras, el algoritmo de empaquetado propuesto es el siguiente.
Dividir los intervalos en seis de números pares nos permite representar cualquier intervalo g en la forma g = i * 12 + t , donde i es el índice de los seis a los que pertenece este intervalo ( i = {0,1,2,3, ...} ) y t es una cola que representa uno de los valores de una definición rígida, acotada e idéntica para cualquiera de los seis del conjunto {2,4,6,8,10,12} . La respuesta de frecuencia del índice resaltado anteriormente es casi exactamente inversamente proporcional a su valor, por lo que es lógico convertir el índice seis en una estructura trivial de un código de longitud variable, un ejemplo del cual se da arriba. Las características de frecuencia de la pinza le permiten dividirlo en dos grupos que pueden codificarse con cadenas de bits de diferentes longitudes: los valores 6 y 12, que se encuentran con mayor frecuencia, están codificados con un bit, los valores 2, 4, 8 y 10, que se encuentran con mucha menos frecuencia, están codificados con dos bits. Por supuesto, se necesita un bit más para distinguir entre estas dos opciones.
Una matriz que contiene paquetes de bits se complementa con campos fijos que especifican los valores iniciales de los datos presentados en el bloque y otras cantidades requeridas para restaurar una secuencia arbitraria simple o secuencial de los simples almacenados en el bloque.
Además de esta estructura de índice de bloque, el uso de códigos de longitud variable se complica por los costos adicionales en comparación con los intervalos de bits fijos.
Cuando se utilizan intervalos de tamaño fijo, determinar el bloque en el que buscar un número primo por su número de serie es una tarea bastante simple, porque el número de intervalos por bloque se conoce de antemano. Pero la búsqueda de una solución simple al valor más cercano no tiene una solución directa. Alternativamente, puede usar alguna fórmula empírica que le permita encontrar el número de bloque aproximado con el intervalo requerido, después de lo cual tendrá que buscar el bloque deseado mediante una búsqueda exhaustiva.
Para una tabla con códigos de longitud variable, se requiere el mismo enfoque para ambas tareas: tanto para obtener un valor por número como para buscar por valor. Como la longitud de los códigos varía, nunca se sabe de antemano cuántas diferencias se almacenan en un bloque en particular y en qué bloque reside el valor deseado. Se determinó experimentalmente que con un tamaño de bloque de 512 bytes (que incluye algunos bytes de encabezado), la capacidad del bloque puede llegar hasta el 10-12 por ciento del valor promedio. Los bloques más pequeños dan una dispersión relativa aún mayor. Al mismo tiempo, el valor promedio de la capacidad del bloque en sí mismo tiende a disminuir lentamente a medida que crece la tabla. La selección de fórmulas empíricas para la determinación inexacta del bloque inicial para buscar el valor deseado tanto por número como por valor es una tarea no trivial. Alternativamente, puede usar indexación más compleja y sofisticada.
Eso, de hecho, es todo.
A continuación, las sutilezas de compresión de una tabla principal utilizando códigos de longitud variable y las estructuras asociadas con ella se describen de manera más formal y detallada, y se proporciona el código para las funciones de empaquetar y desempaquetar intervalos en C.
El resultado
La cantidad de datos traducidos de la Tabla 1TPrimo a códigos de longitud variable, complementada por una estructura de índice de bloque, también descrita a continuación, ascendió a 26,309,295,104 bytes (24.5 GB), es decir, la relación de compresión alcanza 11.4. Obviamente, al aumentar la profundidad de bits, la relación de compresión aumentará.
El tiempo de transmisión de 280 GB de la tabla 1TPrimo en el nuevo formato fue de 1 hora. Este es el resultado esperado después de los experimentos con intervalos de empaquetado en enteros de un solo byte. En ambos casos, la traducción de la tabla fuente consiste principalmente en operaciones de archivos y casi no carga el procesador (en el segundo caso, la carga es aún mayor debido a la mayor complejidad computacional del algoritmo). El tiempo de acceso a los datos tampoco es muy diferente de los intervalos de un solo byte, pero el tiempo para desempaquetar un bloque completo del mismo tamaño tomó 1.5 μs, debido a la mayor complejidad del algoritmo para extraer códigos de longitud variable.
La tabla (Fig. 10) resume las características volumétricas de las tablas de números primos mencionadas en este texto.
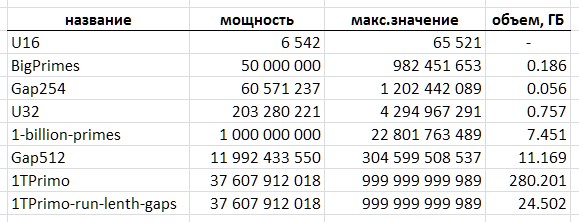
Descripción del algoritmo de compresión
Términos y notación
P (prime): P1=3, P2=5, P3=7 ... Pn, Pn1 son números primos de acuerdo con sus números de serie. Una vez más (y por última vez) enfatizo que
P0=2 es un número primo virtual; en aras de la uniformidad formal, este número está físicamente excluido de la lista de números primos.
G (gap) - el intervalo entre dos primos consecutivos Gn = Pn1 - Pn; G={2,4,6,8 ...} Gn = Pn1 - Pn; G={2,4,6,8 ...} .
D (dense) : reducido a un intervalo de forma monolítica: D = G/2 -1; D={0,1,2,3 ...} D = G/2 -1; D={0,1,2,3 ...} . Los seis intervalos en la forma monolítica se parecen a {0,1,2,3,4,5}, {6,7,8,9,10,11}, {12,13,14,15,16,17} etc.
Q (quotient) - índice de los seis reducido a una forma monolítica, Q = D div 6; Q={0,1,2,3 ...} Q = D div 6; Q={0,1,2,3 ...}
R (remainder) : el resto de los seis monolíticos R = D mod 6. R siempre tiene un valor en el rango {0,1,2,3,4,5} .
Los valores Q y R obtenidos por el método anterior de cualquier intervalo arbitrario G , debido a sus características de frecuencia estables, están sujetos a compresión y almacenamiento en forma de paquetes de bits de longitud variable, que se describen a continuación. Las cadenas de bits que codifican los valores Q y R en un paquete se crean de diferentes maneras: para codificar el índice Q , S la cadena de bits del prefijo H , el flujo F y el bit auxiliar S , y el grupo de bits del infijo X y el bit auxiliar A se utilizan para codificar el resto R
A (arbiter) : un bit que determina el tamaño del infijo X : 0: infijo de un bit, 1: dos bits.
X (infix) : X (infix) 1 o 2 bits, junto con el bit de árbitro R tabular (la tabla también muestra la frecuencia de los primeros seis con dichos infijos como referencia):
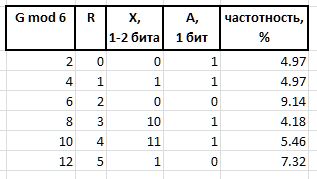
F (fluxion) es una fluxion, una derivada del índice Q longitud variable L={0,1,2...} , diseñada para distinguir entre la semántica de cadenas de bits (), 0, 00, 000, o 1, 01, 001 , etc. d.
Una cadena de unidades de longitud L se expresa como 2^L - 1 (el signo ^ significa exponenciación). En notación C, se puede obtener el mismo valor con la expresión 1<<L - 1 . Entonces el valor de fluxia de longitud L se puede obtener de Q expresión
F = Q - (1 << L - 1),
y restaurar Q de fluxia por expresión
Q = (1 << L - 1) + F.
Como ejemplo, para las cantidades Q = {0..15} , se obtendrán las siguientes cadenas de bits de fluxia:
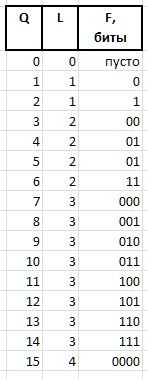
Los últimos dos campos de bit necesarios para empaquetar / restaurar valores son:
H (header) : prefijo, una cadena de bits establecida en 0.
S (stop) : bit de detención establecido en 1, que finaliza el prefijo.
De hecho, estos bits se procesan primero en cadenas de bits, le permiten determinar durante el desempaquetado o establecer durante el empaquetado el tamaño del flujo y el comienzo de los campos de árbitro y flujo, inmediatamente después del bit de detención.
W (width) : el ancho del código completo en bits.
La estructura completa del paquete de bits se muestra en la Fig. 11:
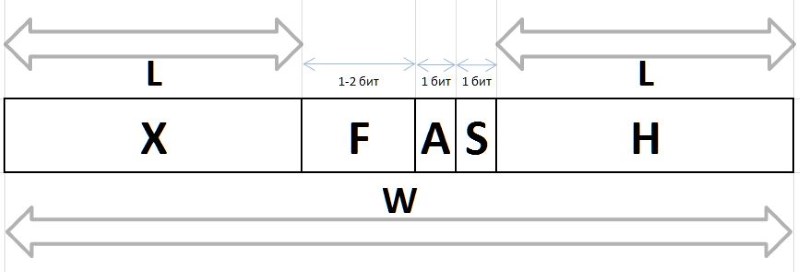
Los valores de Q y R recuperados de estas cadenas nos permiten restaurar el valor inicial del intervalo:
D = Q * 6 + R,
G = (D + 1) * 2,
y la secuencia de intervalos restaurados le permite restaurar los números primos originales a partir de un valor base dado del bloque (bloque inicial de intervalos) al agregarle todos los intervalos de este bloque en secuencia.
Para trabajar con cadenas de bits, se utiliza una variable entera de 32 bits, en la que se procesan los bits menos significativos y después de usarlos, los bits se desplazan hacia la izquierda al empaquetar o hacia la derecha al desempacar.
Estructura de bloque
Además de las cadenas de bits, un bloque contiene información necesaria para buscar o agregar bits, así como para determinar el contenido de un bloque.
// // typedef unsigned char BYTE; typedef unsigned short WORD; typedef unsigned int LONG; typedef unsigned long long HUGE; typedef int BOOL; #define TRUE 1 #define FALSE 0 #define BLOCKSIZE (256) // : , #define HEADSIZE (8+8+2+2+2) // , #define BODYSIZE (BLOCKSIZE-HEADSIZE) // . // typedef struct { HUGE base; // , HUGE card; // WORD count; // WORD delta; // base+delta = WORD offset; // BYTE body[BODYSIZE]; // } crunch_block; // , put() get() crunch_block block; // . // NB: len/val rev/rel // , , // . static struct tail_t { BYTE len; // S A BYTE val; // , A - S BYTE rev; // BYTE rel; // } tails[6] = { { 4, 3, 2, 3 }, { 4, 7, 5, 3 }, { 3, 1, 0, 4 }, { 4,11, 1, 4 }, { 4,15, 3, 4 }, { 3, 5, 4, 4 } }; // BOOL put(int gap) { // 1. int Q, R, L; // (), (), int val = gap / 2 - 1; Q = val / 6; R = val % 6; L = -1; // .., 0 - 1 val = Q + 1; while (val) { val >>= 1; L++; } // L val = Q - (1 << L) + 1; // val <<= tails[R].len; val += tails[R].val; // val <<= L; // L += L + tails[R].len; // // 2. val L buffer put_index if (block.offset + L > BODYSIZE * 8) // ! return FALSE; Q = (block.offset / 8); // , R = block.offset % 8; // block.offset += L; // block.count++; // block.delta += gap; if (R > 0) // { val <<= R; val |= block.body[Q]; L += R; } // L = L / 8 + ((L % 8) > 0 ? 1 : 0); // while (L-- > 0) { block.body[Q++] = (char)val; val >>= 8; } return TRUE; } // int get_index; // // int get() { if (get_index >= BODYSIZE * 8) return 0; // int val = *((int*)&block.body[get_index / 8]) >> get_index % 8; // 4 if (val == 0) return -1; // ! int Q, R, L, F, M, len; // , , , , L = 0; while (!(val & 1)) { val >>= 1; L++; } // - if ((val & 3) == 1) // R = (val >> 2) & 1; // else R = ((val >> 2) & 3) + 2; // len = tails[R].rel; get_index += 2 * L + len; val >>= len; M = ((1 << L) - 1); // F = val & M; // Q = F + M; // return 2 * (1 + (6 * Q + tails[R].rev)); // }
Mejoras
Si alimentamos la base de intervalos obtenida al mismo archivador de 7 zip, luego de una hora y media de trabajo intensivo en un servidor de 8 núcleos, logra comprimir el archivo de entrada en casi un 5%. Es decir, en la base de datos de intervalos de longitud variable desde el punto de vista del archivador, todavía hay algo de redundancia. Por lo tanto, hay razones para especular un poco (en el buen sentido de la palabra) sobre el tema de reducir aún más la redundancia de datos.
El determinismo fundamental de la secuencia de intervalos entre los números primos permite hacer cálculos exactos de la eficiencia de codificación por un método u otro. En particular, los bocetos pequeños (y bastante caóticos) permitieron sacar una conclusión fundamental acerca de las ventajas de codificar seises sobre triples, y sobre las ventajas del método propuesto sobre los códigos triviales de longitud variable (Fig. 12):
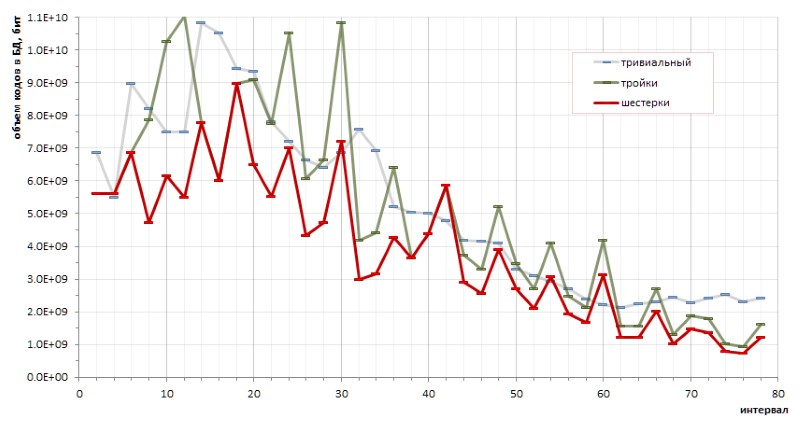
Sin embargo, los molestos máximos del gráfico rojo insinúan de manera transparente que puede haber otros métodos de codificación que harían el gráfico aún más suave.
Otra dirección sugiere verificar la frecuencia de intervalos consecutivos. Por consideraciones generales: dado que los intervalos 6, 12 y 18 son los más comunes en una población de números primos, es probable que se encuentren con mayor frecuencia en pares (dobletes), triples (trillizos) y combinaciones similares de intervalos. Si la repetibilidad de los duplets (y tal vez incluso los tripletes ... ¡bueno, de repente!) Resulta ser estadísticamente significativa en la masa total de intervalos, entonces tiene sentido traducirlos en algún código separado.
El experimento a gran escala revela un cierto predominio de dobletes individuales sobre otros. Sin embargo, si se espera un liderazgo absoluto para el par (6,6) - 1.37% de todos los dobletes - entonces los otros ganadores de esta calificación son mucho menos obvios:
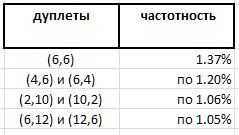
Y, dado que el doblete (6,6) simétrico, y todos los otros dobletes señalados son asimétricos y se encuentran en la clasificación de dobles espejo con la misma frecuencia, parece que el registro récord del doblete (6,6) en esta serie debería dividirse a la mitad entre dobles no distinguibles (6,6) y (6,6) , lo que los lleva 0.68% hasta el borde de la lista de premios. Y esto una vez más confirma la observación de que no se pueden realizar conjeturas verdaderas sobre los números primos sin sorpresas.
Las estadísticas de los trillizos también demuestran el liderazgo de tales triples de intervalos, que no encajan del todo en el supuesto especulativo que procede de la frecuencia más alta de los intervalos 6, 12, 18. En orden decreciente de popularidad, los líderes de frecuencia entre los trillizos son los siguientes:

etc.
Sin embargo, me temo que los resultados de mis especulaciones serán de menor interés para los programadores que para los matemáticos, tal vez debido a las correcciones inesperadas hechas por la práctica en conjeturas intuitivas. Es poco probable que sea posible exprimir cualquier dividendo sustancial del porcentaje mencionado de frecuencia a favor de un aumento adicional en la relación de compresión, mientras que la complejidad del algoritmo amenaza con crecer de manera muy significativa.
Limitaciones
Ya se señaló anteriormente que el aumento en el valor máximo de los intervalos en relación con la capacidad de los primos es muy, muy lento. En particular, se puede ver en la Fig. 6 que el intervalo entre cualquier primo que se puede representar en el formato de un entero sin signo de 64 bits obviamente será menor que 1600.
La implementación descrita le permite empaquetar y desempaquetar correctamente cualquier valor de intervalo de 18 bits (de hecho, el primer error de empaquetado ocurre con un intervalo de entrada de 442358). No tengo suficiente imaginación para suponer que la base de datos de intervalos primos puede crecer a tales valores: por casualidad, está en algún lugar alrededor de enteros de 100 bits, y para calcular con mayor precisión la pereza. En un caso de incendio, expandir el rango de intervalos a veces no será difícil.
Gracias por leer este lugar :)