
Nuevo lenguaje en ciencia de datos. Julia es un idioma bastante raro en Rusia, aunque se ha utilizado en el extranjero durante 5 años (también me sorprendieron). No hay fuentes en ruso, así que decidí presentar un caso en el punto de Julia, tomado de un libro maravilloso. La mejor manera de aprender un idioma es comenzar a escribir algo en él.
Y para que esto también atraiga la atención, use el aprendizaje automático.Hola habrozhitelam.
Hace algún tiempo, comencé a aprender el nuevo idioma de Julia. Bueno, como nuevo. Esto es algo entre Matlab y Python, la sintaxis es muy similar y el lenguaje en sí está escrito en C / C ++. En general, la historia de la creación, qué, por qué y por qué está en Wikipedia y en un par de artículos sobre Habré.
Lo primero que comenzó mi estudio del idioma, es cierto, Google on Coursera,
el curso en
línea de Google en inglés. Allí, sobre la sintaxis básica +, se escribe en paralelo un mini proyecto sobre la predicción de enfermedades en África. Conceptos básicos y práctica inmediata. Si necesita un certificado, compre la versión completa. Fui gratis. La diferencia entre esta versión es que nadie verificará sus pruebas y DZ. Para mí era más importante conocerme que un certificado. (Leer atascado 50 dólares)
Después de eso decidí que debería leer un libro sobre Julia. Google emitió una lista de libros y siguió estudiando reseñas y reseñas, eligió uno de ellos y ordenó en Amazon. Las versiones de libros siempre son más agradables de leer y dibujar a lápiz.
El libro se llama
Julia for Data Science por Zacharias Voulgaris, PhD. El extracto que quiero presentar contiene muchos errores tipográficos en el código que arreglé y, por lo tanto, presentará la versión de trabajo + mis resultados.
kNN
Este es un ejemplo de la aplicación del algoritmo de clasificación para el método de los vecinos más cercanos. Probablemente uno de los algoritmos de aprendizaje automático más antiguos. El algoritmo no tiene una fase de aprendizaje y es bastante rápido. Su significado es bastante simple: para clasificar un nuevo objeto, necesita encontrar "vecinos" similares del conjunto de datos (base de datos) y luego determinar la clase votando.
Haré una reserva de inmediato para que Julia tenga paquetes ya preparados, y es mejor usarlos para reducir el tiempo y los errores. Pero este código es, en cierto modo, indicativo de la sintaxis de Julia. Es más conveniente para mí aprender un nuevo idioma con ejemplos que leyendo extractos secos de la forma general de una función.
Entonces, lo que tenemos en la entrada:
Datos de entrenamiento X (muestra de entrenamiento),
etiquetas de datos de entrenamiento x (etiquetas correspondientes),
datos de prueba Y (selección de prueba),
número de vecinos k (número de vecinos).
Necesitará 3 funciones: función de
cálculo de distancia, función de clasificación y
principal .
La conclusión es: tomar un elemento del conjunto de prueba, calcular la distancia desde él a los elementos del conjunto de entrenamiento. Luego seleccionamos los índices de esos
k elementos que resultaron ser lo más cercanos posible. Asignamos el elemento bajo prueba a la clase que es la más común entre
k vecinos más cercanos.
function CalculateDistance{T<:Number}(x::Array{T,1}, y::Array{T,1}) dist = 0 for i in 1:length(x) dist += (x[i] - y[i])^2 end dist = sqrt(dist) return dist end
La función principal del algoritmo. La matriz de distancias entre los objetos del entrenamiento y las muestras de prueba, las etiquetas del conjunto de entrenamiento y el número de "vecinos" más cercanos llegan a la entrada. El resultado son las etiquetas predichas para nuevos objetos y las probabilidades de cada etiqueta.
function Classify{T<:Any}(distances::Array{Float64,1}, labels::Array{T,1}, k::Int) class = unique(labels) nc = length(class) #number of classes indexes = Array(Int,k) #initialize vector of indexes of the nearest neighbors M = typemax(typeof(distances[1])) #the largest possible number that this vector can have class_count = zeros(Int, nc) for i in 1:k indexes[i] = indmin(distances) #returns index of the minimum element in a collection distances[indexes[i]] = M #make sure this element is not selected again end klabels = labels[indexes] for i in 1:nc for j in 1:k if klabels[j] == class[i] class_count[i] +=1 end end end m, index = findmax(class_count) conf = m/k #confidence of prediction return class[index], conf end
Y, por supuesto, todas las funciones.
Tendremos un conjunto de entrenamiento
X en la entrada, el conjunto de entrenamiento marca
x , el conjunto de prueba
Y y el número de "vecinos"
k .
En la salida, recibiremos las etiquetas predichas y las probabilidades correspondientes de cada premio de clase.
function main{T1<:Number, T2<:Any}(X::Array{T1,2}, x::Array{T2,1}, Y::Array{T1,2}, k::Int) N = size(X,1) n = size(Y,1) D = Array(Float64,N) #initialize distance matrix z = Array(eltype(x),n) #initialize labels vector c = Array(Float64, n) #confidence of prediction for i in 1:n for j in 1:N D[j] = CalculateDistance(X[j,:], vec(Y[i,:])) end z[i], c[i] = Classify(D,x,k) end return z, c end
Prueba
Probemos lo que tenemos. Por conveniencia, guardamos el algoritmo en el archivo kNN.jl.
La base está prestada del
curso Open Machine Learning . El conjunto de datos se llama Samsung Human Activity Recognition. Los datos provienen de los acelerómetros y giroscopios de los teléfonos móviles Samsung Galaxy S3, y también se conoce el tipo de actividad de una persona con un teléfono en el bolsillo, ya sea que caminó, se paró, se acostó, se sentó o subió / bajó las escaleras. Resolveremos el problema de determinar el tipo de actividad física precisamente como un problema de clasificación.
Las etiquetas corresponderán a lo siguiente:
1 - caminar
2 - sube las escaleras
3 - bajando las escaleras
4 - asiento
5 - una persona estaba parada en este momento
6 - la persona estaba mintiendo
include("kNN.jl") training = readdlm("samsung_train.txt"); training_label = readdlm("samsung_train_labels.txt"); testing = readdlm("samsung_test.txt"); testing_label = readdlm("samsung_test_labels.txt"); training_label = map(Int, training_label) testing_label = map(Int, testing_label) z = main(training, vec(training_label), testing, 7) n = length(testing_label) println(sum(testing_label .== z[1]) / n)
Resultado: 0.9053274516457415La calidad se evalúa mediante la proporción de objetos pronosticados correctamente para toda la muestra de prueba. Parece que no es tan malo. Pero mi objetivo es más bien mostrarle a Julia, y que él tiene un lugar para estar en Data Science.
Visualización
A continuación, quería intentar visualizar los resultados de la clasificación. Para hacer esto, debe construir una imagen bidimensional, con 561 signos y sin saber cuáles son los más significativos. Por lo tanto, para reducir la dimensionalidad y el posterior diseño de datos en el subespacio ortogonal de las características, se decidió utilizar el
Análisis de componentes principales (PCA). En Julia, como en Python, hay paquetes listos para usar, por lo que simplificamos un poco nuestra vida.
using MultivariateStats #for PCA A = testing[1:10,:] #PCA for A M_A = fit(PCA, A'; maxoutdim = 2) Jtr_A = transform(M_A, A'); #PCA for training M = fit(PCA, training'; maxoutdim = 2) Jtr = transform(M, training'); using Gadfly #shows training points and uncertain point pl1 = plot(training, layer(x = Jtr[1,:], y = Jtr[2,:],color = training_label, Geom.point), layer(x = Jtr_A[1,:], y = Jtr_A[2,:], Geom.point)) #predicted values for uncertain points from testing data z1 = main(training, vec(training_label), A, 7) pl2 = plot(training, layer(x = Jtr[1,:], y = Jtr[2,:],color = training_label, Geom.point), layer(x = Jtr_A[1,:], y = Jtr_A[2,:],color = z[1], Geom.point)) vstack(pl1, pl2)
En la primera figura, se marcan el conjunto de entrenamiento y varios objetos del conjunto de prueba, que deberán asignarse a su clase. En consecuencia, la segunda figura muestra que estos objetos fueron marcados.

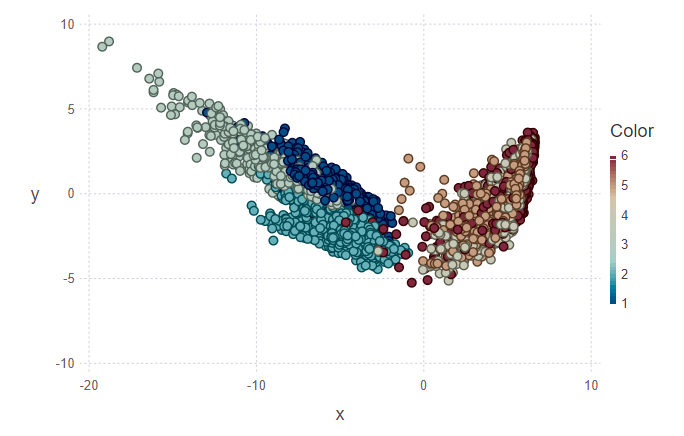
println(z[1][1:10], z[2][1:10]) > [5, 5, 5, 5, 5, 5, 5, 5, 5, 4][1.0, 0.888889, 0.888889, 0.888889, 1.0, 1.0, 1.0, 1.0, 0.777778, 0.555556]
Mirando las imágenes, quiero hacer la pregunta "¿por qué son tan feos estos grupos?". Te lo explicaré. Los grupos individuales no están delineados muy claramente debido a la naturaleza de los datos y al uso de PCA. Para la PCA, solo caminar y subir escaleras es como una clase: la clase de movimiento. En consecuencia, la segunda clase es la clase de descanso (sentado, de pie, acostado, que no son muy distinguibles entre sí). Y por lo tanto, una separación clara se puede rastrear en dos clases en lugar de seis.
Conclusión
Para mí, esto es solo una inmersión inicial en Julia y el uso de este lenguaje en el aprendizaje automático. Por cierto, en el que también soy más probable que sea un aficionado que un profesional. Pero mientras estoy interesado, continuaré estudiando este asunto más profundamente. Muchas fuentes extranjeras apuestan por Julia. Bueno, espera y verás.
PD: Si es interesante, puedo contarte en las siguientes publicaciones sobre las características de la sintaxis, sobre el IDE, con cuya instalación tuve problemas.