Este artículo analiza el uso de la biblioteca geométrica de funciones de WebGeometry para construir modelos de poliedros complejos. La biblioteca está escrita en Javascript.
Un enlace a GitHub con un ejemplo que proporciona un ejemplo simple de uso de la biblioteca. Comentarios y críticas son bienvenidos.
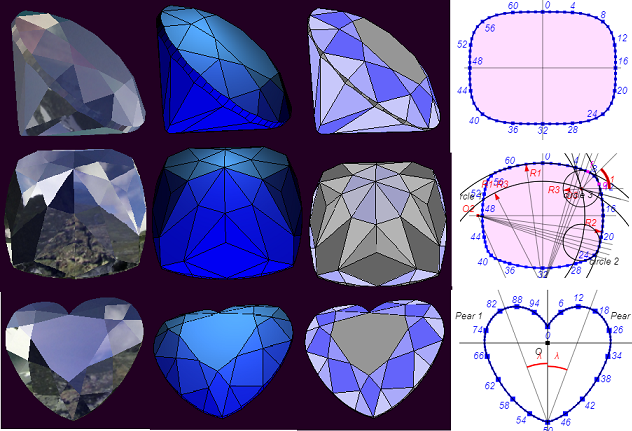
La biblioteca ThreeJS se usa para mostrar modelos precalculados usando funciones de la biblioteca WebGeometry. El lienzo HTML5 se usa para mostrar elementos de modelos planos individuales y mostrar información de soporte.
La tecnología WebGL y las bibliotecas creadas sobre esta base, como ThreeJS y BadylonJS, se utilizan en Internet para implementar una variedad de propósitos relacionados con los gráficos 3D. Pero básicamente se utilizan para mostrar modelos tridimensionales ya preparados en un navegador (previamente creado, por ejemplo, en programas
3ds Max o
Blender ). Si nos enfrentamos a la tarea de crear un modelo paramétrico, es decir, un modelo para el cual, en el proceso de mostrar un objeto terminado en el navegador, podemos cambiar sus elementos individuales estableciendo los parámetros del modelo apropiados (por ejemplo, aumentar el ángulo de una determinada cara), necesitamos tener Un conjunto de funciones geométricas que le permitirán crear un modelo para que en el futuro exista la posibilidad de variar interactivamente la forma de los elementos individuales del modelo o de todo el modelo. Para resolver este problema, necesitamos un conjunto de funciones en el lenguaje Javascript que implemente los métodos utilizados en geometría analítica. La biblioteca debe tener funciones para crear líneas, planos y círculos, encontrar puntos (o líneas) de su intersección, crear planos inclinados y mucho más. Las bibliotecas ThreeJS y BadylonJS tienen algunas de estas características, pero el número de acciones realizadas con ellas no le permitirá completar todas las tareas que surgen al construir un modelo paramétrico. Hay varias bibliotecas Javascript más puramente matemáticas. De estos,
glMatrix y
Sylvester son los más utilizados. La biblioteca
glMatrix está diseñada principalmente para trabajar con vectores, matrices y cuaterniones, pero no hay funciones para trabajar con líneas y planos en ella. La biblioteca
Sylvester tiene estas funciones, pero están presentes en una cantidad bastante limitada. Sin embargo, hay varios libros que describen la implementación de métodos de geometría analítica en C / C ++. Los programas C / C ++ correspondientes pueden usarse como prototipos para crear una biblioteca matemática en Javascript. Por lo tanto, cuando decidí crear modelos paramétricos tridimensionales de cortes de diamantes para mostrarlos en un navegador, elegí la biblioteca ThreeJS solo para mostrar modelos ya calculados; no se usó para calcular la forma de los modelos. Para el cálculo del formulario en sí, se creó la biblioteca WebGeometry. Esta biblioteca se basó en las funciones geométricas utilizadas anteriormente en C / C ++, que traduje al lenguaje Javascript. Consideremos las etapas de la construcción de un modelo piramidal (corte de diamante del tipo Pirámide).
En la
primera etapa, necesitamos dibujar la vista prevista del modelo y luego numerar sus vértices. La siguiente figura muestra la numeración de los vértices y los nombres de los elementos de corte incluidos en el modelo de corte piramidal.

Después de eso, se requiere formar caras a partir de los vértices numerados. Por ejemplo, para la cara del sitio y las caras de la corona, escriba la siguiente secuencia de vértices (el primer vértice duplicado de la cara indica que la cara ha terminado):
0, 3, 2, 1, 0;
Las caras deben estar en sentido antihorario. El archivo pyramid_index.js contiene el código fuente para atravesar todas las caras de la pirámide y comentarios detallados. El resultado del rastreo se escribe en la matriz index_cut.
En la
segunda etapa, podemos colorear las caras del modelo. Este paso es opcional si no necesitamos un color. Supongamos que queremos colorear un modelo piramidal de la siguiente manera:
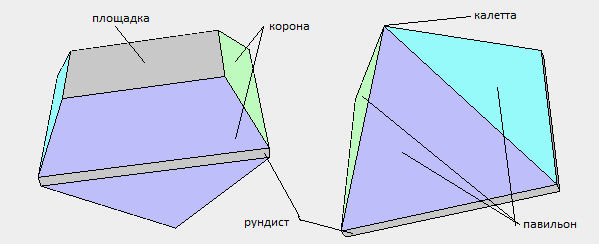
Para este fin, se crea el archivo pyramid_colors.js en el que se encuentra la función facet_colors (), que escribe los colores de todas las caras en la matriz de colores.
En la
tercera etapa , después de que se numeran todos los vértices y se registran las secuencias transversales de todos los vértices de las caras, es necesario establecer los parámetros del modelo y luego calcular las coordenadas de todos sus vértices. Por supuesto, se supone que ya hemos delineado el algoritmo de construcción para nosotros mismos y descubrimos cómo se ubicarán todas las caras del modelo en el espacio. Para la pirámide, elegiremos los siguientes parámetros, que determinarán los tamaños de sus partes individuales y de todo el modelo en su conjunto:
var DEGREE = 0.01745329251994;
La elección de los parámetros la determina el desarrollador del modelo. Por ejemplo, en lugar de establecer dos parámetros para dos ángulos de inclinación de la corona, puede especificar un solo parámetro para dos ángulos a la vez, entonces estos ángulos siempre serán los mismos. Puede ingresar un parámetro que determine el tamaño del sitio. En este caso, se requiere no establecer la altura de la corona o no establecer la inclinación de sus caras. Otra opción para elegir parámetros es hacer que algunos parámetros sean computables. En este caso, al cambiar algunos parámetros, otros pueden cambiar su valor inicial. Por ejemplo, si suponemos que para la pirámide hemos definido un parámetro para establecer el ángulo de inclinación de las caras coronales, otro parámetro para la altura de la corona y otro parámetro que establecerá el tamaño del área, entonces al cambiar el ángulo de las caras nos veremos obligados a cambiar el tamaño del área o altura de la corona Por otro lado, si cambia el parámetro que establece el tamaño de la almohadilla, el valor del parámetro que establece la altura o la pendiente de las caras coronales cambiará automáticamente. No se utiliza la opción asociada con la aplicación de los parámetros calculados en este programa, así como en la construcción de los otros modelos de corte presentados en el sitio.
En la
cuarta etapa , se calculan las coordenadas de los vértices del modelo. Los datos iniciales para el cálculo son los valores de los parámetros del modelo y cómo imaginamos su apariencia. El archivo pyramid_verts.js contiene el texto fuente (con comentarios detallados) de la función de cálculo de vértices del modelo, que se llama VerticesCalculation. Es con este cálculo que las funciones de la biblioteca WebGeometry se utilizan en esta función. Los resultados del cálculo de las coordenadas de los vértices se ingresan en la matriz de vértices. Tenga en cuenta que en el programa para encontrar las coordenadas de los vértices, se utilizan secuencias separadas de números para los vértices que forman la corona (cuatro vértices), los vértices que forman la faja (cuatro vértices) y los vértices que forman el pabellón (en el modelo de pirámide, solo el vértice está incluido en el pabellón). Esta opción de numeración de vértices adicional se usa para una orientación más fácil por parte del programador entre los vértices de corte, ya que el número de vértices suele exceder 100
En la
quinta etapa, después de completar el cálculo de las coordenadas de los vértices, se requiere construir mediante programación el poliedro (poliedro) del modelo. Los datos iniciales para su construcción son matrices creadas previamente de index_cut, colores y vértices. Un modelo de poliedro puede representarse simplemente como un conjunto de caras que unen un poliedro en el espacio. La función CreatePolyhedron está en el archivo polyhedron.js. Como resultado del trabajo de esta función, se crea una matriz de polígonos (polígonos) en la que consiste el modelo tridimensional. Cada polígono se describe mediante la siguiente función (de hecho, es una función constructora llamada por el nuevo operador al crear un nuevo polígono):
function Polygon() { this.IndexFacet = [];
Dado que WebGL y la biblioteca ThreeJS creada sobre su base funcionan con primitivas triangulares, se triangula para cada cara del modelo. Se supone que todas las caras del modelo son polígonos convexos. En última instancia, la función CreatePolyhedron toma todos los pasos necesarios para crear estructuras de datos que describan completamente todas las caras del poliedro de tal manera que puedan pasarse a las funciones de la biblioteca ThreeJS para mostrar el modelo en la pantalla.
En la
sexta etapa , el modelo se muestra en la pantalla utilizando las funciones ThreeJS. De manera estándar, se crean la escena, el renderizador y la cámara. Para examinar el modelo de corte desde todos los lados, el programa Pyramid usa el elemento orbitControls. Al crear otros modelos de corte, para inspeccionar los cortes desde todos los lados, no utilicé orbitControls, sino que introduje la capacidad de rotar el modelo en sí. Luego creamos las mallas modelo. Puedes hacer dos cosas.
En el primer método, consideramos el modelo de corte como un conjunto de mallas de cara separadas. En este caso, cada cara es un objeto 3D separado. Con esta representación del modelo, el proceso de seleccionar una cara individual usando el elemento Three.JS, que tiene el nombre de raycaster, es bastante simple. Además, este método puede complementarse con la creación de mallas de segmentos que bordean cada cara.
En la segunda forma, consideramos el modelo de corte como un solo objeto, representado por una sola malla que incluye inmediatamente todas las caras del modelo. Este método es conveniente de usar cuando se muestra un modelo usando sombreadores. Este método no se usa en el modelo de corte Pyramid, pero se usa para crear octágono, Brilliant y otros modelos de corte que se pueden ver en mi sitio web.
En la
séptima etapa , se crean botones y funciones adjuntas que les permiten cambiar el valor de los parámetros que determinan la forma y el tamaño del modelo. Cuando se presiona un botón, se llama a una función que aumenta o disminuye el valor del parámetro correspondiente. Esto significa que es necesario volver a calcular el valor de las coordenadas de los vértices del modelo. Después del recuento, se verifica la corrección del modelo recién construido. Por ejemplo, se determina si algunos valores están fuera de tolerancia. En el caso de los modelos de corte de diamante, esto generalmente se reduce a verificar si el corte convexo permanece después de su reconstrucción. La comprobación del bulto es la siguiente. A través de cada cara se dibuja un plano en el que se encuentra esta cara, y luego se determina la posición de cada vértice del modelo en relación con este plano. Todos los vértices deben ubicarse en el mismo lado de este plano. Si el modelo se considera incorrecto, el parámetro vuelve a su valor original y el modelo se reconstruye nuevamente. Para los modelos de corte que tienen una faja no convexa (solo este elemento de algunos cortes, como el Corazón, puede ser no convexo), la convexidad se verifica por separado para la corona y por separado para el pabellón. El rundista, sin embargo, está excluido del cheque. Para modelos simples, puede restringirse a una simple verificación de parámetros. Por ejemplo, si estamos construyendo un modelo de una casa, entonces el techo no debe tener más de una cierta altura de antemano. Por lo tanto, simplemente configurando la restricción de este parámetro en magnitud, obtenemos el resultado deseado. Después de agregar los botones de parámetros, es muy conveniente mostrar visualmente el valor de cada parámetro cuando cambia después de hacer clic en el botón. Para hacer esto, se crea un lienzo bidimensional HTML5 y al lado del botón correspondiente se muestra el valor del parámetro.
Por lo tanto, examinamos todas las etapas de la construcción de un modelo utilizando el ejemplo de la Pirámide. Para la pirámide (así como para todos los demás modelos en el sitio), creé otro programa Pyramid_text.html. El ejemplo de este programa muestra cómo puede mostrar texto tridimensional para numerar los vértices de un modelo. Si alguien quiere saber cómo se construyen los modelos complejos, entonces debería considerar construir modelos
(vea GitHub) en la siguiente secuencia:
Octágono Un modelo que demuestra la creación de planos de varias maneras y trabajando con estos planos. Al construir un modelo, también se utilizan los métodos utilizados al trabajar con vectores y líneas en el espacio.
Brillante Este es el corte de diamante clásico y más común. Algunos elementos de la construcción de un modelo tridimensional de este corte se utilizan en el futuro al crear facetas MoonMarquise, MoonPear y Heart. La forma en que se calcula la faja de este corte, que tiene la forma de un superelipse, se muestra por separado en el programa BrilliantGirdlt.html. En este programa, la línea de cintura se construye en un lienzo bidimensional (lienzo).
MoonMarquise . El corte Marquesa, como Brilliant, es uno de los clásicos cortes de diamantes. A diferencia de una faceta simple de este tipo (Marquesa), las llamadas "facetas lunares" se agregan a la faceta MoonMarquise del Pabellón. El cortador MoonMarquise está formado por dos arcos de elipses. Una construcción detallada de esta faja sobre lienzo se muestra en el programa MarquiseGirdle.html. El texto de este programa tiene comentarios detallados sobre la construcción. Observamos un punto con respecto al cálculo de la línea de cintura: usa la propiedad de una tangente a una elipse. Se considera, por ejemplo, en el libro "Curso de geometría analítica" (el autor de este libro es N.I. Muskhelishvili).
MoonPear El mero de corte MoonPear está formado por los arcos de tres elipses. Su construcción se basa en la construcción de la faja de corte Marquesa, pero es más compleja. Para ver la línea de cintura de Marquise y cómo dividir la gundist en segmentos, ejecute el programa PearGirdle.html.
Corazon El corte "corazón" es uno de los cortes clásicos, pero tiene, en contraste con la mayoría de los cortes, una forma de faja no convexa. El rudista de corte de corazón está formado por dos fajas de corte de pera inclinadas una respecto a la otra. En el lienzo, puede ver la línea de cintura ejecutando el programa HeartGirdle.html. Construir un corte de corazón es todo un desafío.
Cruz de Malta El cortador del corte "Cruz de Malta" está hecho en forma de "almohada" (cojín). Los esquejes con tal faja se han generalizado recientemente. La línea de esta faja es ocho arcos de círculos conjugados: cuatro arcos principales que bordean la almohada en cuatro lados y cuatro arcos de menor tamaño que combinan los arcos principales de la almohada en las esquinas de la faja. Al ejecutar los programas CushionGirdle_1.html y CushionGirdle_2.html, puede ver la forma de la línea de la faja, el trabajo de todos los parámetros que establecen su forma y la división de la faja en segmentos.
Estrella pentagonal . El cortador estelar pentagonal está formado por una línea que lleva el nombre del epitrocoide. El epitrocoide es una curva relacionada con el cicloide. En el programa Wavy_Pentagon_Girdle.html, al cambiar los valores de los parámetros, puede cambiar la "ondulación" de la faja e incluso cambiar el pentágono a un polígono con un número diferente de salientes ("pétalos"). Sin embargo, debe recordarse que el modelo de este corte en sí está construido para el valor del parámetro "Número de pétalos" igual a 5.
Como se mencionó anteriormente, para todos los modelos anteriores, los programas se crean mostrando el número de vértices de corte. En estos programas, se realiza un cambio entre la visualización directa de todos los vértices del modelo y la indicación de los números de vértice para la corona, la faja y el pabellón por separado. Suponga que en el modelo de corte maltés desea crear un plano que pase por los vértices con los números 84, 88 y 145. En lugar de usar estos números para identificar los puntos a través de los cuales pasa el plano al crear un plano usando la función CreatePlaneThreePoints, una grabación usando un separado Numeración de picos para la faja y el pabellón:
var plane = new Plane3D(); plane.CreatePlaneThreePoints(girdle[68], girdle[72], crown[1]);
Cabe señalar que los programas que muestran números de vértices modelo funcionan muy lentamente (al menos en mi computadora). Pueden pasar varios segundos antes de que se complete la salida de los números de vértice del modelo.
Para resumir todo lo anterior, en mi opinión, la elección de poliedros (modelos de corte) para demostrar el funcionamiento de las funciones geométricas es una de las mejores opciones. Después de examinar el trabajo de los ejemplos anteriores, podemos proceder a la creación de objetos geométricos relacionados con campos de actividad completamente diferentes que el modelado de corte de diamante.