Solución numérica de modelos matemáticos de objetos dados por sistemas de ecuaciones diferenciales.

Introducción

En el modelado matemático de varios dispositivos técnicos, se utilizan sistemas de ecuaciones diferenciales no lineales. Dichos modelos se utilizan no solo en tecnología, sino también en economía, química, biología, medicina y gestión.

El estudio del funcionamiento de tales dispositivos requiere la solución de estos sistemas de ecuaciones. Dado que la mayor parte de tales ecuaciones son no lineales y no estacionarias, a menudo es imposible obtener su solución analítica.

Es necesario utilizar métodos numéricos, el más famoso de los cuales es el método Runge - Kutta [1]. En cuanto a Python, en publicaciones sobre métodos numéricos, por ejemplo [2,3], hay muy pocos datos sobre el uso de Runge - Kutta, y no hay datos sobre su modificación al método Runge - Kutta - Felberg.

Actualmente, gracias a su interfaz simple, la función odeint del módulo scipy.integrate tiene la mayor distribución en Python. La segunda función oda de este módulo implementa varios métodos, incluido el método Runge-Kutta-Felberg de cinco rangos mencionado, pero, debido a su universalidad, tiene un rendimiento limitado.

El propósito de esta publicación es un análisis comparativo de los medios listados para resolver numéricamente sistemas de ecuaciones diferenciales con un autor modificado bajo Python usando el método Runge-Kutta-Felberg. La publicación también proporciona soluciones a problemas de valor límite para sistemas de ecuaciones diferenciales (SDE).

Breves datos teóricos y reales sobre los métodos y software considerados para la solución numérica de CDS

El problema de Cauchy

Para una ecuación diferencial del enésimo orden, el problema de Cauchy consiste en encontrar una función que satisfaga la igualdad:



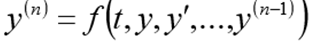
y condiciones iniciales



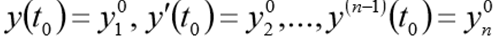
Antes de resolver este problema debe reescribirse en la forma de los siguientes CDS

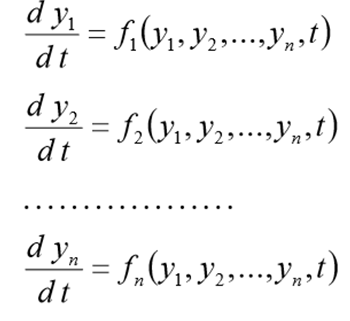
(1)

con condiciones iniciales



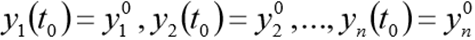Scipy.integrate module

El módulo tiene dos funciones ode () y odeint (), diseñadas para resolver sistemas de ecuaciones diferenciales ordinarias (ODE) de primer orden con condiciones iniciales en un punto (problema de Cauchy). La función ode () es más universal, y la función odeint () (integrador ODE) tiene una interfaz más simple y resuelve bien la mayoría de los problemas.

Función Odeint ()

La función odeint () tiene tres argumentos obligatorios y muchas opciones. Tiene el siguiente formato odeint (func, y0, t [, args = (), ...]) El argumento func es el nombre Python de la función de dos variables, la primera de las cuales es la lista y = [y1, y2, ..., yn ], y el segundo es el nombre de la variable independiente.

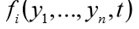
La función Func debería devolver una lista de n valores de función para un valor dado del argumento independiente t. De hecho, la función func (y, t) implementa el cálculo de los lados derechos del sistema (1).

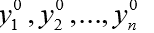
El segundo argumento y0 de odeint () es una matriz (o lista) de valores iniciales en t = t0.

El tercer argumento es una serie de puntos de tiempo en los que desea obtener una solución al problema. En este caso, el primer elemento de esta matriz se considera t0.

La función odeint () devuelve una matriz de tamaño len (t) x len (y0). La función odeint () tiene muchas opciones que controlan su funcionamiento. Las opciones rtol (error relativo) y atol (error absoluto) determinan el error de cálculo ei para cada valor de yi de acuerdo con la fórmula



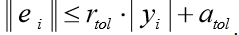
Pueden ser vectores o escalares. Por defecto



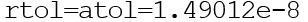Función Ode ()

La segunda función del módulo scipy.integrate, que está diseñado para resolver ecuaciones y sistemas diferenciales, se llama ode (). Crea un objeto ODE (tipo scipy.integrate._ode.ode). Al tener un enlace a dicho objeto, uno debería usar sus métodos para resolver ecuaciones diferenciales. De manera similar a la función odeint (), la función ode (func) implica reducir el problema a un sistema de ecuaciones diferenciales de la forma (1) y usar su función de los lados derechos.

La única diferencia es que la función del lado derecho func (t, y) acepta una variable independiente como primer argumento, y la lista de valores de las funciones deseadas como segundo. Por ejemplo, la siguiente secuencia de instrucciones crea un ODE que representa una tarea Cauchy.

Runge - Método Kutta

Al construir algoritmos numéricos, asumimos que existe una solución a este problema diferencial, que es única y tiene las propiedades de suavidad necesarias.

En la solución numérica del problema de Cauchy

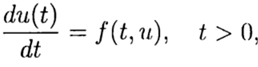
(2)

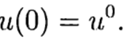
(3)

de acuerdo con la solución conocida en el punto t = 0, es necesario encontrar una solución de la ecuación (3) para otra t. En la solución numérica del problema (2), (3), usaremos una cuadrícula uniforme, por simplicidad, en la variable t con un paso t> 0.

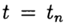
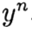
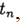
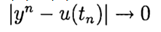
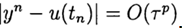
Una solución aproximada al problema (2), (3) en el punto denotar . El método converge en un punto si a las . El método tiene un orden de precisión pth si , p> 0 para . El esquema de diferencia más simple para una solución aproximada al problema (2), (3) es

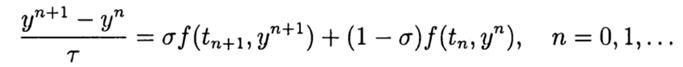
(4)

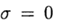
En tenemos un método explícito y en este caso el esquema de diferencia se aproxima a la ecuación (2) con el primer orden. Diseño simétrico en (4) tiene un segundo orden de aproximación. Este esquema pertenece a la clase de implícito: para determinar la solución aproximada en una nueva capa, es necesario resolver el problema no lineal.

Es conveniente construir esquemas de aproximación explícitos de segundo y mayor orden basados ​​en el método predictor-corrector. En la etapa del predictor (predicción), se utiliza un esquema explícito.

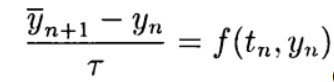
(5)

y en la etapa correctora (refinamiento), un diagrama



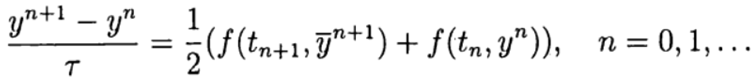
En los métodos Runge - Kutta de un solo paso, las ideas del predictor-corrector se realizan más plenamente. Este método está escrito en forma general:

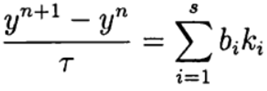
(6)

donde



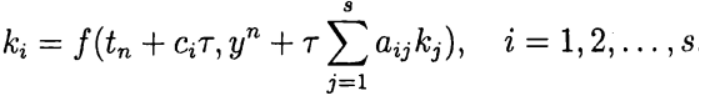
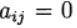
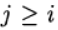
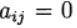
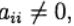
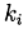
La fórmula (6) se basa en los cálculos de s de la función f y se llama s-stage. Si a las tenemos el método explícito Runge - Kutta. Si para j> 1 y entonces determinado implícitamente a partir de la ecuación:

(7)

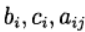
Se habla de este método Runge - Kutta como implícito en diagonal. Parámetros determinar una variante del método Runge - Kutta. Se utiliza la siguiente representación del método (tabla de carnicero)



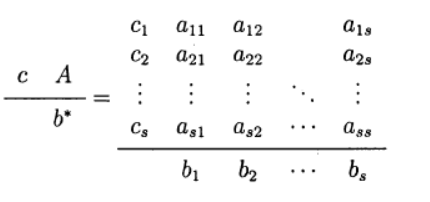
Uno de los más comunes es el método explícito de cuarto orden Runge - Kutta.

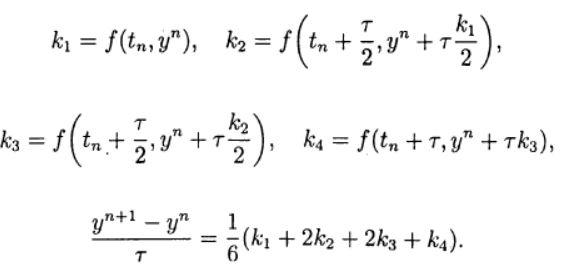
(8)

Runge - Kutta - Método Felberg

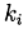
Doy el valor de los coeficientes calculados método

(9)

En vista de (9), la solución general tiene la forma:

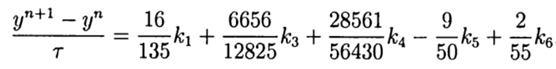
(10)

Esta solución proporciona el quinto orden de precisión, queda por adaptarlo a Python.

Experimento computacional para determinar el error absoluto de la solución numérica de una ecuación diferencial no lineal 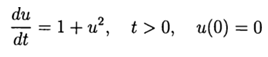utilizando las funciones def odein (), def oden () del módulo scipy.integrate y los métodos Runge - Kutta y Runge - Kutta - Felberg adaptados a Python

Obtenemos:









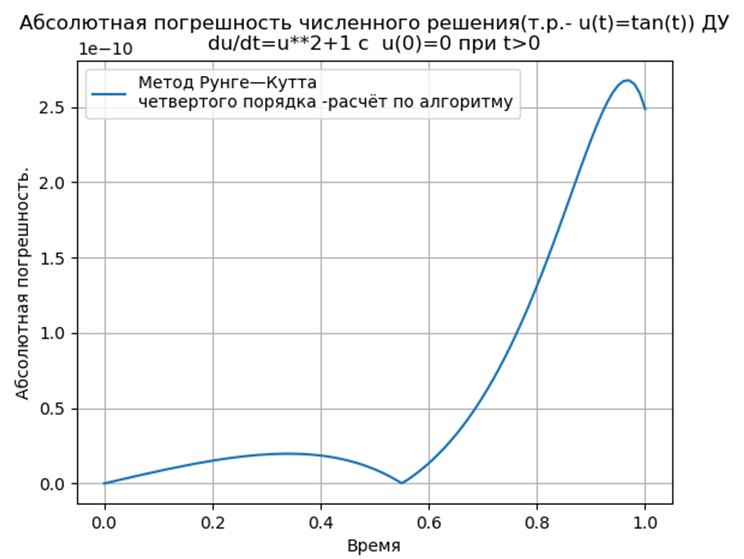
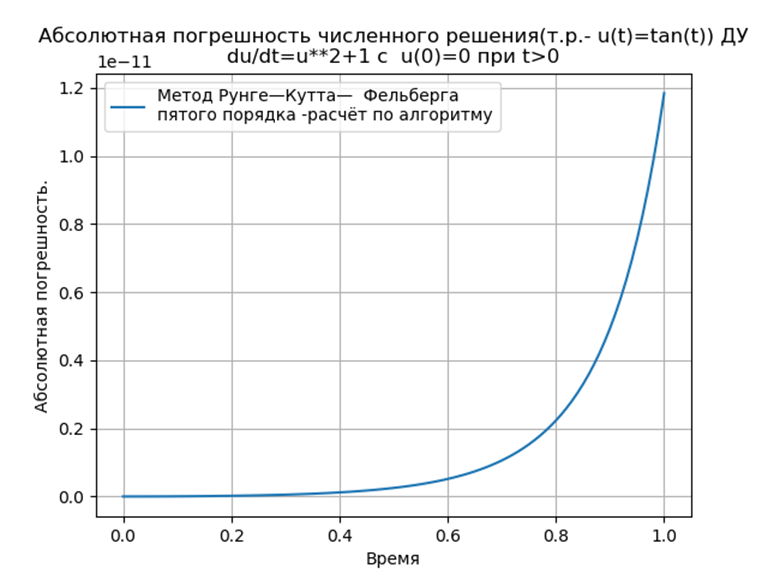
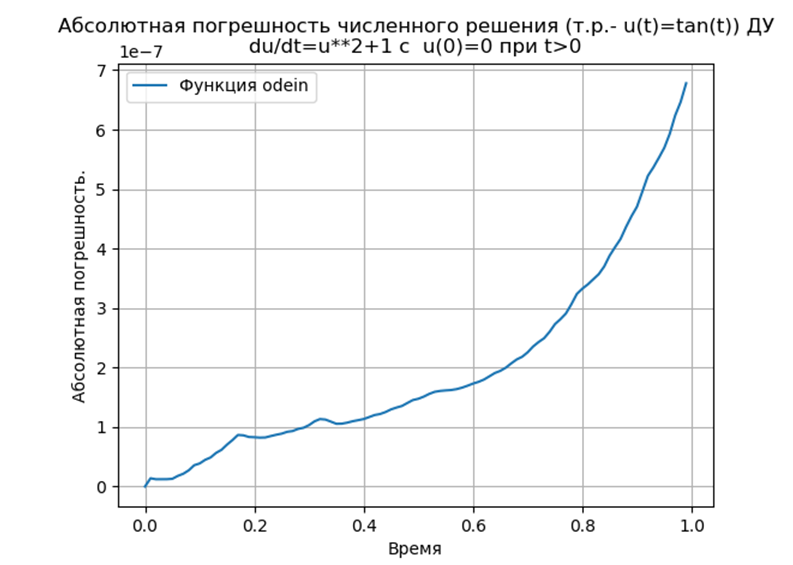
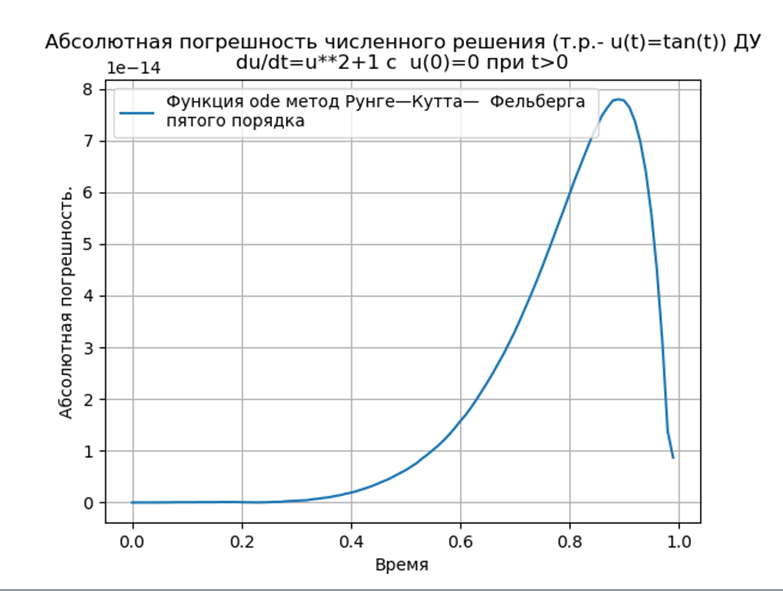Conclusión

Los métodos Runge - Kutta y Runge - Kutta - Felberg adaptados a Python tienen un absoluto más bajo que una solución que usa la función odeint, pero más que una solución que usa la función edu. Es necesario realizar un estudio de rendimiento.

Un experimento numérico que compara la velocidad de la solución numérica de la SDE cuando se usa la función oda con el atributo dopri5 (método Runge - Kutta de quinto orden) y se usa el método Runge - Kutta - Felberg adaptado a Python

Se realiza un análisis comparativo utilizando el problema modelo dado en [2] como ejemplo. Para no repetir la fuente, presentaré la formulación y solución del problema modelo de [2].

Resolvamos el problema de Cauchy, que describe el movimiento de un cuerpo arrojado con una velocidad inicial v0 en un ángulo α con respecto al horizonte bajo el supuesto de que la resistencia del aire es proporcional al cuadrado de la velocidad. En forma vectorial, la ecuación de movimiento tiene la forma



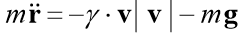
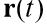
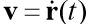
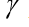
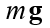
donde Es el radio del vector del cuerpo en movimiento, Es el vector de velocidad del cuerpo, - coeficiente de arrastre, vector fuerzas de peso corporal de masa m, g - aceleración de la gravedad.



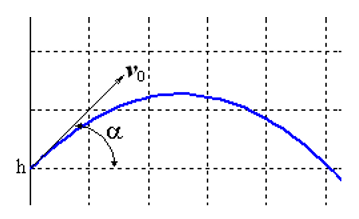
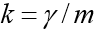
La peculiaridad de esta tarea es que el movimiento termina en un punto desconocido en el tiempo cuando el cuerpo cae al suelo. Si designado , luego en forma de coordenadas tenemos un sistema de ecuaciones:



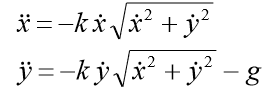
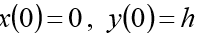
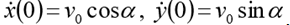
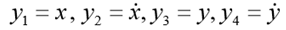
Las condiciones iniciales deben agregarse al sistema: (h altura inicial) . Poner . Luego, el sistema ODE de primer orden correspondiente toma la forma:



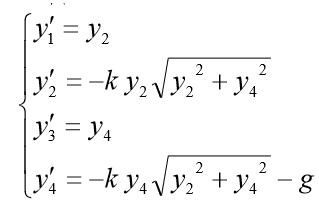
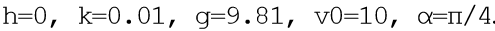
Para el problema modelo ponemos . Omitiendo una descripción bastante extensa del programa, solo daré una lista de los comentarios para los cuales, creo, el principio de su funcionamiento será claro. El programa ha agregado una cuenta regresiva para el análisis comparativo.



Obtenemos:

Tiempo de vuelo = 1.2316 Distancia = 5.9829 Altura = 1.8542
Tiempo de vuelo = 1.1016 Distancia = 4.3830 Altura = 1.5088
Tiempo de vuelo = 1.0197 Distancia = 3.5265 Altura = 1.2912
Tiempo de vuelo = 0.9068 Distancia = 2.5842 Altura = 1.0240
Tiempo para el problema del modelo: 0.454787



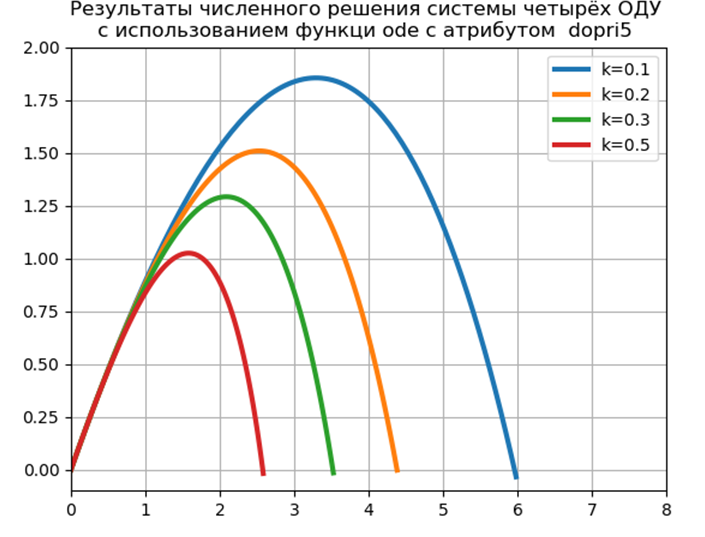
Para implementar una solución numérica del CDS usando herramientas de Python sin usar módulos especiales, propuse e investigué la siguiente función:

def increment(f, t, y, tau
k1=tau*f(t,y)
k2=tau*f(t+(1/4)*tau,y+(1/4)*k1)
k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2)
k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3)
k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4)
k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5)
return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6

La función de incremento (f, t, y, tau) proporciona el quinto orden del método de solución numérica. Otras características del programa se pueden encontrar en la siguiente lista:


Obtenemos:

Tiempo para el problema del modelo: 0.259927



Conclusión

La implementación de software propuesta para el problema del modelo sin el uso de módulos especiales tiene un rendimiento casi dos veces más rápido que con la función ode, pero no debemos olvidar que ode tiene una mayor precisión de la solución numérica y la posibilidad de elegir un método de solución.

Resolver un problema de valor límite con condiciones de límite separadas por hilos

Damos un ejemplo de un problema específico de valor límite con condiciones de límite separadas por hilos:

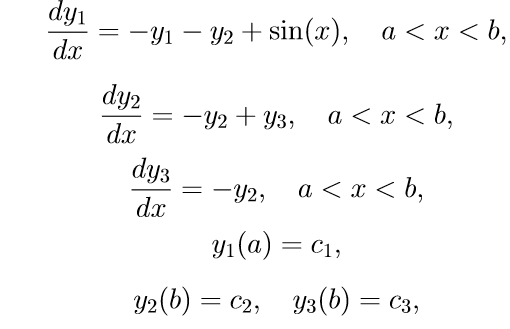
(11)

Para resolver el problema (11), utilizamos el siguiente algoritmo:

1. Resolvemos las tres primeras ecuaciones no homogéneas del sistema (11) con las condiciones iniciales

Introducimos la notación para resolver el problema de Cauchy:


2. Resolvemos las tres primeras ecuaciones homogéneas del sistema (11) con las condiciones iniciales

Introducimos la notación para resolver el problema de Cauchy:


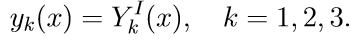
3. Resolvemos las tres primeras ecuaciones homogéneas del sistema (11) con las condiciones iniciales



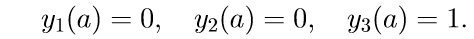
Introducimos la notación para resolver el problema de Cauchy:



4. La solución general del problema del valor límite (11) usando las soluciones de los problemas de Cauchy se escribe como una combinación lineal de soluciones:

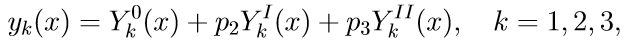
donde p2, p3 son algunos parámetros desconocidos.

5. Para determinar los parámetros p2, p3, utilizamos las condiciones de contorno de las dos últimas ecuaciones (11), es decir, las condiciones para x = b. Sustituyendo, obtenemos un sistema de ecuaciones lineales con respecto a p2, p3 desconocido:
(12)
Resolviendo (12), obtenemos las relaciones para p2, p3.

Usando el algoritmo anterior usando el método Runge - Kutta - Felberg, obtenemos el siguiente programa:


Obtenemos:

y0 [0] = 0.0
y1 [0] = 1.0
y2 [0] = 0.7156448588231397
y3 [0] = 1.324566562303714
y0 [N-1] = 0.9900000000000007
y1 [N-1] = 0.1747719838716767
y2 [N-1] = 0.8
y3 [N-1] = 0.5000000000000001
Tiempo para el problema del modelo: 0.070878

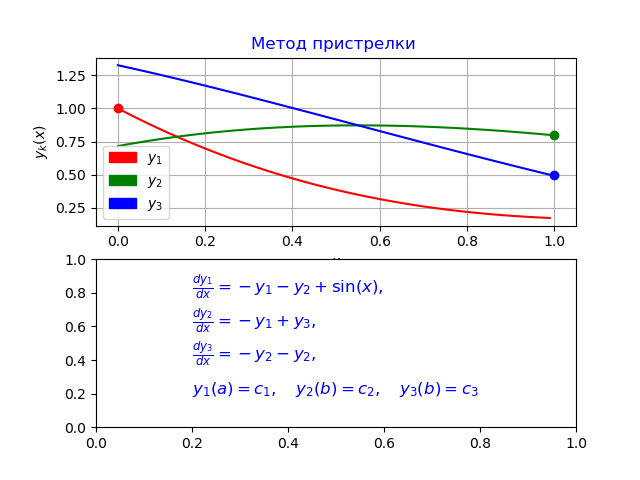
Conclusión

El programa desarrollado por mí difiere del error dado en [3], que confirma el análisis comparativo de la función odeint dada al comienzo del artículo con el método Runge - Kutta - Felberg implementado en Python.

Referencias

1. Solución numérica de modelos matemáticos de objetos definidos por sistemas compuestos de ecuaciones diferenciales.

2. Introducción a Python científico.

3. N.M. Polyakova, E.V. Shiryaeva Python 3. Creación de una interfaz gráfica de usuario (utilizando el ejemplo de resolución del problema del valor límite para ecuaciones diferenciales lineales ordinarias mediante el método de disparo). Rostov del Don 2017.