Manipulador "manual"

Una vez, durante mi segundo año en la universidad, me dieron la tarea: cocinar algo "más o menos" para confirmar el alto rango de "futuro ingeniero de robótica". En esta nota de pathos, entré en las profundidades de la conciencia para buscar ideas. Después de un corto viaje, surgió una idea sobre el dispositivo, cuya teoría de la creación quiero compartir con el público.

La esencia del desarrollo es esta. Considere el manipulador habitual de 5 ejes (el diagrama estructural cinemático se muestra en la figura a continuación). Sus capacidades cuando se mueve en el espacio son amplias: es capaz de hacer movimientos en 5 coordenadas, y al mismo tiempo, es decir. 3 coordenadas a lo largo de los tres ejes XYZ y rotación alrededor de dos de ellos. En este caso, el elemento de trabajo del manipulador puede ocupar cualquier posición en el espacio de trabajo y al mismo tiempo mantener la orientación requerida del cuerpo de trabajo (sin contar la rotación del elemento de trabajo alrededor de su propio eje).



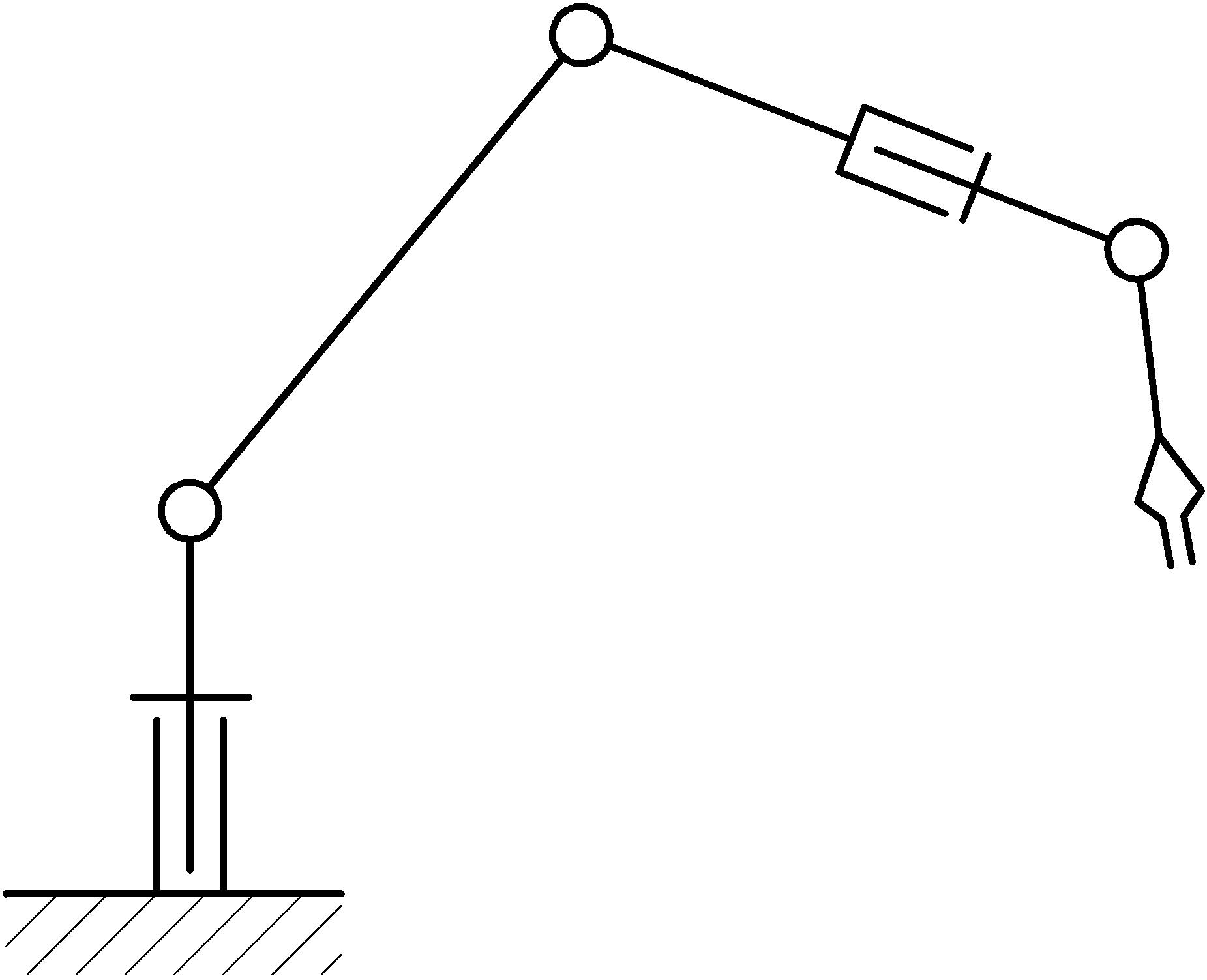
Este diseño se refiere a manipuladores de tipo antropomórfico y, por lo tanto, es capaz, aproximadamente, por supuesto, de reproducir el movimiento de una mano humana. Discutiendo sobre esta tesis, surgió la idea de que sería interesante hacer que el manipulador copie remotamente los movimientos de mi mano en tiempo real. De modo que solo puse un sensor en mi mano que lee los movimientos de la mano (tanto lineales como angulares), y esta cosa mecánica los repetirá después de mí. Como el manipulador puede realizar las funciones de mover y orientar el cuerpo de trabajo, así, con la ayuda de la mano, una persona puede mover y orientar la palma de su mano, por lo tanto, estos dos procesos son similares y pueden representarse como un proceso común: capturar el movimiento de la mano en tiempo real.


Esto completa la declaración del problema. Ahora analicemos la tarea (el lenguaje no se convierte en llamarla "tarea técnica"). Es necesario desarrollar dos dispositivos estructuralmente independientes: el manipulador en sí y el dispositivo de seguimiento del movimiento, que está montado en el brazo. Esto será seguido por el lento proceso de crear descripciones matemáticas, compilar un algoritmo y escribir software. Dividimos el proyecto en tres partes:

1. El desarrollo del manipulador.
2. Desarrollo de un dispositivo para rastrear el movimiento del brazo.
3. Todo lo demás

Brevemente sobre cada una de las etapas:

1. Aquí todo es trivial ... En CAD, diseñamos la estructura, realizamos dibujos de piezas y fabricación, luego ensamblamos. Luego calculamos la cinemática y escribimos nuestro propio software, que ocultará las llamadas de bajo nivel a las unidades.
2. En esta etapa, determinamos el tipo de sensores, diseñamos un diagrama de circuito, hacemos una placa de circuito impreso, desarrollamos un algoritmo para determinar la posición en el espacio, escribimos software.
3. En realidad, por lo que fueron las etapas anteriores: hacer que el manipulador obedezca al propietario. Aquí desarrollo un algoritmo para convertir coordenadas en el campo de trabajo del manipulador.

1. El desarrollo del manipulador.

En este proyecto, como se mencionó anteriormente, utilizamos un manipulador con 5 grados de libertad. Tal cantidad de grados de libertad es suficiente, porque incluyen tres desplazamientos lineales y dos rotacionales. Los dos últimos son necesarios para la orientación del cuerpo de trabajo, ya que la dirección de PO en el espacio se puede especificar en forma de un vector, y el vector definitivamente se puede restaurar desde dos ángulos de rotación (sin tener en cuenta la longitud). En este caso, necesitamos cinco coordenadas generalizadas, igual al número de ejes.

Los enlaces del manipulador están conectados por pares cinemáticos rotacionales de la quinta clase. El diseño del manipulador es estándar para su tipo (el esquema cinemático se presenta al principio del artículo). Tiene una cama fija, con la cual se conecta el sistema de coordenadas básico, un soporte giratorio, al que se unen los enlaces móviles restantes, conectados en una cadena. Se une un cuerpo de trabajo al eslabón final (brida), en este caso su imitación en forma de puntero en forma de flecha (ver imagen a continuación).




El modelo 3D fue construido en CAD "Compass 3D". Material de las piezas: madera contrachapada de 4 mm y PLA para piezas de plástico. Las piezas de madera contrachapada se cortaron en una máquina láser, las piezas de plástico se imprimieron en una impresora 3D. Los servos digitales Dynamixel AX-12 se utilizan como unidades de eje. La apariencia del manipulador se asemeja a un insecto vil, del que recibió el apodo de "Komar".

La descripción matemática de la cinemática.

En esta etapa, es necesario calcular la cinemática directa e inversa del manipulador. La tarea directa es determinar la posición de los enlaces en relación con algún sistema de coordenadas básico utilizando los valores conocidos de las coordenadas generalizadas (en este caso, los ángulos de rotación de los enlaces). La tarea inversa a ella se llama cinemática inversa o inversa, consiste en determinar los parámetros de las coordenadas generalizadas para lograr la posición y orientación deseadas del cuerpo de trabajo del manipulador.

Comencemos calculando la cinemática inversa. Describamos el esquema geométrico del manipulador, a partir del cual las relaciones geométricas de interés para nosotros serán claras.



La posición requerida está representada por un vector de radio $$$\ vec {r}$ . Vale la pena explicar por qué el vector $$$\ vec {r}$ dibujado al punto de brida, y no al punto final de la RO. Dado que conocemos de antemano la orientación del cuerpo de trabajo (yo mismo lo determino según algunos requisitos), es necesario que el punto de la brida esté en el lugar correcto, indicado como un vector $$$\ vec {r}$ . Este vector se obtiene restando del vector de radio $$$\ vec {R}$ dibujado al punto final de PO, su vector de orientación $$$\ vec {v_0}$ , relativo a BSK, es decir:

$$ $$\ vec {r} = \ vec {R} - \ vec {v_0}$$

Considere la transición del punto de brida a la posición deseada. Se lleva a cabo mediante la rotación de los enlaces a y b (los representé en forma de vectores) en las bisagras A , B y C. El origen del sistema de coordenadas base (BSC) se coloca en el punto de la bisagra B. El eje de rotación de la bisagra A se dirige a lo largo del eje Z , los ejes B y C se dirigen perpendicularmente a Z.

Cuando se cumplan todas las formalidades, vayamos al grano. Para resolver el problema de la cinemática inversa, utilicé un enfoque geométrico debido a la simplicidad del diseño del manipulador. De la geometría se puede ver que el vector $$$\ vec {r}$ igual a la suma de los vectores de enlace $$$\ vec {a}$ y $$$\ vec {b}$ . Ángulos $$$\ theta$ , $$$\ gamma_1$ , $$$\ gamma_2$ - los ángulos de rotación de los enlaces A , B y C, respectivamente.
Considere un triángulo delimitado por vectores $$$\ vec {r}$ , $$$\ vec {a}$ y $$$\ vec {b}$ . Desde este triángulo, por el teorema del coseno, encontramos los ángulos $$$\ alpha$ y $$$\ beta$ . Deje que las longitudes de los vectores sean iguales a:

$$ $$| \ vec {r} | = r \ quad | \ vec {a} | = a \ quad | \ vec {b} | = b$$

Escribimos el teorema del coseno con respecto a los ángulos deseados:

$$ $$b ^ 2 = a ^ 2 + r ^ 2-2ar \ cos (\ alpha) \\ r ^ 2 = a ^ 2 + b ^ 2-2ab \ cos (\ beta)$$

Expresa los ángulos $$$\ alpha$ y $$$\ beta$ :

$$ $$\ alpha = \ arccos \ left (\ frac {a ^ 2 + r ^ 2-b ^ 2} {2ar} \ right) \ quad \ beta = \ arccos \ left (\ frac {a ^ 2 + b ^ 2 -r ^ 2} {2ab} \ right)$$

Se puede ver en el diagrama geométrico que:

$$ $$\ theta = \ arctan = \ left (\ frac {r_y} {r_x} \ right) \ quad \ omega = \ arcsin = \ left (\ frac {r_z} {r} \ right)$$

Entonces:

$$ $$\ gamma_1 = \ omega + \ alpha \ quad \ gamma_2 = 180 ^ \ circ- \ beta$$

Finalmente, la transición de una coordenada lineal a los ángulos de rotación de los enlaces se realiza mediante las fórmulas:

$$ $$\ theta = arctan \ left (\ frac {r_y} {r_x} \ right) \\ \ gamma_1 = arcsin \ left (\ frac {r_z} {r} \ right) + arccos \ left (\ frac {a ^ 2 + r ^ 2-b ^ 2} {2ab} \ right) \\ \ gamma_2 = 180 ^ \ circ-arccos \ left (\ frac {a ^ 2 + b ^ 2-r ^ 2} {2ar} \ right) $$$

Ahora que ha movido el punto de brida a la posición deseada, debe orientar adecuadamente el cuerpo de trabajo. Para hacer esto, necesitas saber las coordenadas del vector $$$\ vec {v}$ relativo al punto de la brida, es decir coordenadas en base al sistema de coordenadas local (LSC) - $$${E '}$ , cuyo comienzo se encuentra en el punto de brida del manipulador.

$$ $$E '= \ left [\ vec {x}' \ \ vec {y} '\ \ vec {z}' \ right]$$

Vector $$$\ vec {x} '$ dirigido por el enlace b , vector $$$\ vec {y} '$ - a lo largo del eje del eslabón giratorio f1 .
Para encontrar una base $$$E '$ Definimos la matriz de transición de BSK (con base $$$E_0$ ) y LSK. Esta matriz se obtiene mediante una combinación de rotaciones en las bisagras A , B y C :

$$ $$E '= CE_0$$

donde

$$ $$C = R_CR_BR_A$$

Porque matriz $$$E_0$ es soltero, entonces:

$$ $$E '= C = R_CR_BR_A$$

Matriz $$$C$ Se calcula multiplicando las matrices de rotación alrededor del eje por un ángulo .
Definimos una función que calcula esta matriz:

$$ $$f = axisAngle2rotMat (eje, ángulo)$$

El eje se toma en forma de un vector como una columna de la matriz obtenida por rotaciones anteriores, y los ángulos ya se calcularon anteriormente.

$$ $$C_A = axisAngle2rotMat (E_0 ^ {\ langle3 \ rangle}, \ theta) \\ C_ {BA} = R_BC_A = axisAngle2rotMat (C_A ^ {\ langle2 \ rangle}, \ gamma_1) C_A \\ C_ {CBA} = R_CC_ { BA} = axisAngle2rotMat (C_ {BA} ^ {\ langle2 \ rangle}, \ gamma_1) C_ {BA}$$

Como resultado, obtenemos:

$$ $$C = C_ {CBA} \ quad E '= C$$

Deje que el vector del cuerpo de trabajo en BSK $$$\ vec {v_0}$ . Entonces la igualdad es verdadera:

$$ $$\ vec {v_0} = E '\ vec {v}$$

Desde aquí expresamos $$$\ vec {v}$ - vector del cuerpo de trabajo en la base $$$E '$ es decir relativo al punto de brida:

$$ $$\ vec {v} = E '^ T \ vec {v_0}$$

Ahora, conociendo el vector PO, podemos calcular los ángulos de rotación de los ejes de orientación f1 y f2


Para mover el PO a una posición dada, debe hacer una rotación en las esquinas $$$\ varphi_1$ y $$$\ varphi_2$ . La figura muestra que

$$ $$\ varphi_1 = arctan \ left (\ frac {v_y} {v_z} \ right) \ quad \ varphi_2 = arcsin \ left (\ frac {\ sqrt {v_y ^ 2 + v_z ^ 2}} {V} \ right)$$

donde $$$V = | \ vec {v} | = \ sqrt {v_x ^ 2 + v_y ^ 2 + v_z ^ 2}$ - la longitud del cuerpo de trabajo,
$$$v_x, v_y, v_z$ - coordenadas vectoriales $$$\ vec {v}$ .

El software del manipulador se divide en dos niveles, superior e inferior. El nivel superior está escrito en Matlab en forma de biblioteca y varios métodos de comando, el inferior, en el microcontrolador Atmega328. La tarea del nivel superior es formular los comandos enviados al microcontrolador. Su tarea es conseguir que el equipo y, de acuerdo con él, instale las unidades en la posición correcta. De esta forma, el sistema de control resultó ser confiable (hasta ahora ...) y cómodo de usar.


La formulación del comando y el envío desde el nivel superior es el siguiente: el usuario en la ventana de comando Matlab llama a una función de la biblioteca (por ejemplo, la función de simplemente moverse a un punto), indica los argumentos necesarios (generalmente estas son las coordenadas y la orientación del PO). Después de las consideraciones matemáticas descritas anteriormente, registradas en la biblioteca, se calculan los ángulos de rotación de los ejes y, si es necesario, la velocidad de rotación. Después de un protocolo simple, ensamblamos el comando y lo enviamos al microcontrolador de nivel inferior a través del puerto serie COM.

Algunas palabras sobre la biblioteca escrita. Tiene las siguientes funciones a su disposición:

1. funciones de conexión en serie
2. funciones de movimiento

• hasta cierto punto, con una velocidad constante de todas las unidades
• hasta un punto, con una parada final de todas las unidades (la velocidad de la unidad se selecciona en proporción a su propio ángulo de rotación más grande. Por lo tanto, al final del acercamiento al punto, todas las unidades dejan de moverse)
• hasta cierto punto, con un movimiento suave de cada unidad (en este caso, el gráfico de velocidad se ve como un trapecio con áreas de aceleración, velocidad constante y frenado)
  
  
  Graph

  

  
  
  
  
• hasta un punto, de acuerdo con los ángulos de rotación especificados manualmente de los ejes y la velocidad de rotación

La lista de funciones, por supuesto, se puede ampliar, pero esta funcionalidad fue suficiente para resolver directamente el problema para el que se diseñó el manipulador.

El video muestra el funcionamiento del manipulador.

2. Desarrollo de un dispositivo para rastrear el movimiento del brazo.

Ve al siguiente paso. Aquí deberá diseñar un dispositivo especial que pueda rastrear en tiempo real la posición en la palma de su mano. Además, este proceso se llama "captura de movimiento". Para implementar el plan, decidí usar el sistema de navegación inercial (SINS) basado en tres sensores: un giroscopio, un acelerómetro y un magnetómetro. Un grupo de estos sensores se llama IMU, un sensor (en traducción, este es el mismo PECADO).

Primero, diseñé una placa de circuito impreso con la funcionalidad que necesitaba, en la que coloqué estos tres sensores. Como controlador de procesamiento, elegí (o más bien tomé lo que era) el microcontrolador Atmega2560. Los sensores usados ​​son comunes y baratos en el mercado chino. Estos son sensores de giroscopio y acelerómetro de tres ejes emparejados MPU6050 y magnetómetro HMC5883l.



El algoritmo para calcular la posición en el espacio es bastante simple: primero, determinamos la orientación en forma de la base del sistema de coordenadas local (LSC), que está conectado con los sensores, y finalmente con la palma de la mano.



La orientación se determina en relación con el sistema de coordenadas inicial (NSC), que es esencialmente la posición inicial del dispositivo en el momento del encendido. Las bases de NSC y LSC consisten en vectores de columna de su orth:

$$ $$E_0 = \ left [\ vec {X} \ \ vec {Y} \ \ vec {Z} \ right] = \ left [\ begin {array} {cccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {array} \ right] \\ E '= \ left [\ vec {x}' \ \ vec {y} '\ \ vec {z}' \ right]$$

Están relacionados por la relación:

$$ $$E '= CE_0$$

Donde $$$C$ Es una matriz de transición, también es una matriz de rotación en el espacio. Consideramos la base del NSC como la matriz de identidad. Por lo tanto

$$ $$E '= C$$

.
Después, el vector de aceleración $$$\ vec {A}$ , que se conoce con respecto al LSC, debe determinarse en el NSC. Esto se hace multiplicando el vector de la columna de aceleración por la base LSC:

$$ $$\ vec {A} = E '\ vec {A}'$$

Luego integramos el vector de aceleración obtenido dos veces en el tiempo y obtenemos la distancia, es decir coordenadas:

$$ $$\ vec {r} = \ iint \ vec {A} dt$$

Los primeros intentos de implementar este algoritmo fueron muy ingenuos ... La ingenuidad fue que solo consideraba posible desde el giroscopio, utilizando una integración discreta, obtener una matriz de rotación alrededor del eje. El eje en este caso puede considerarse como un pseudovector de velocidad angular, cuyos componentes (proyección en el eje) son la salida del sensor giroscópico. Y el ángulo, a su vez, se obtiene integrando el módulo vectorial. El entusiasmo inicial y el entusiasmo desaparecieron cuando vi un monstruoso tamaño, la llamada "deriva cero", causada por el error de acumulación debido al error de integración discreta y el ruido intrínseco del sensor. Incluso entonces, pensé que de acuerdo con el acelerómetro, que en reposo muestra el vector, el inverso del vector de aceleración de la gravedad (en adelante denominado el vector de gravedad), puede hacer la corrección de la matriz, pero aquí hay incertidumbre asociada con el hecho de que la corrección es posible solo hasta la rotación del ángulo alrededor del eje Z. La corrección se completará si será posible restaurar la matriz de rotación de una manera alternativa, es decir, sin usar datos de giroscopio.


Entonces es necesario usar otro factor por el cual será posible hacer un ajuste completo de la situación. Este factor es el campo magnético de la Tierra, que, junto con la gravedad en un solo punto del planeta, no cambia con el tiempo (por supuesto, a corto plazo). Se mide utilizando el sensor HMC5883l mencionado anteriormente. En este caso, tenemos dos vectores, que son suficientes para determinar la posición en el espacio en relación con ellos.

Ahora surge una pregunta lógica: "¿cómo hacer esto?" Después de intentos fallidos de responder a esta pregunta, me subí a Internet, donde encontré la información que necesitaba. La tarea de determinar la orientación en el espacio de acuerdo con tres mediciones (velocidad angular, vector de gravedad y vector de campo magnético) también surge en el diseño de aviones aficionados (por ejemplo, helicópteros), por lo que este problema se ha resuelto repetidamente por varios métodos. Un método popular es el llamado filtro Majwick (Sebastian OH Madgwick). Después de leer el artículo original y no entender el inglés, recurrí a una traducción maravillosa (gracias al autor por el trabajo realizado). Mientras profundizaba en el estudio del artículo, cada vez tenía más la idea de intentar escribir mi propio algoritmo de filtro de determinación de posición, dado que en este momento mi nivel de conocimiento en esta área había aumentado significativamente. En aras del interés, "inventar una bicicleta"! Y lo "inventé". A continuación les doy mi razonamiento.

El algoritmo usa las lecturas de los tres sensores. Permítame recordarle que la tarea del algoritmo es calcular la orientación del objeto y compensar la deriva cero del giroscopio, dado el par dado del acelerómetro y el magnetómetro. Como herramienta matemática que describe la posición, se utiliza un cuaternión, porque es conveniente en términos de construcción y optimización del algoritmo y requiere menos operaciones matemáticas para calcularlo, a diferencia de las matrices. El cuaternión de rotación en el espacio es el siguiente:

$$ $$q = \ left [q_1 \ q_2 \ q_3 \ q_4 \ right]$$

Conocer el eje de rotación descrito por el vector normalizado. $$$\ vec {v} = \ left [v_x \ v_y \ v_z \ right]$ y ángulo $$$\ varphi$ (de donde vienen arriba) puedes calcular el cuaternión:

$$ $$q_ {v, \ varphi} = \ left [\ cos \ left (\ frac {\ varphi} {2} \ right) \ \ v_x \ sin \ left (\ frac {\ varphi} {2} \ right) \ \ v_y \ sin \ left (\ frac {\ varphi} {2} \ right) \ \ v_z \ sin \ left (\ frac {\ varphi} {2} \ right) \ right] \ quad (*)$$

Luego, usando solo el giroscopio, en cada iteración del ciclo calcularemos el valor actual del cuaternión de acuerdo con la expresión:

$$ $$q_n ^ G = q_ {n-1} q_ {v, d \ varphi}$$

Aqui $$$q_n ^ G$ - cuaternión en un momento dado. El índice G en la parte superior indica que este valor se refiere a la medida relativa a las lecturas del giroscopio, es decir. velocidad angular; $$$q_ {n-1}$ - el valor del cuaternión en el momento anterior en el tiempo; $$$q_ {v, d \ varphi}$ –Cambiando la posición en un paso de medición, podemos decir un cambio discreto de posición por un ángulo $$$d \ varphi$ para $$$dt$ Es el período de muestreo expresado por el cuaternión de rotación (*).

El siguiente paso en el cálculo es encontrar la matriz de rotación basada en datos de un par de sensores de acelerómetro y magnetómetro. Específicamente, consideramos el vector de gravedad y el vector de inducción del campo magnético de la Tierra, que, como se mencionó anteriormente, son estáticos con respecto a la Tierra y el NSC asociado. Aquí la tesis es la siguiente: conociendo los valores de gravedad e inducción en base al LSC y al NSC, podemos calcular la matriz de transición (rotación) del NSC al LSC y el cuaternión de rotación en el espacio .

Denote por $$$\ vec {G}$ vector de gravedad inicial normalizado. Se puede tomar de la siguiente manera:

$$ $$\ vec {G} = {\ left [0 \ 0 \ 1 \ right]} ^ T$$

A través de $$$\ vec {H}$ denotar el vector de inducción magnética inicial normalizado:

$$ $$\ vec {H} = {\ left [H_x \ H_y \ H_z \ right]} ^ T$$

También se requiere un tercer vector. $$$\ vec {K}$ que está asociado con estos dos. Se obtiene por multiplicación vectorial. $$$\ vec {H}$ en $$$\ vec {G}$ :

$$ $$\ vec {K} = {\ left [K_x \ K_y \ K_z \ right]} ^ T = \ vec {H} \ times \ vec {G} = {\ left [H_y \ -H_x \ 0 \ right]} ^ T$$

Ahora se forma la matriz $$$M_0$ que caracteriza la posición inicial, es decir NSC, ya que en el momento inicial, el LSC coincide con el NSC. La matriz se obtiene de los componentes de los vectores. $$$\ vec {H}$ , $$$\ vec {G}$ y $$$\ vec {K}$ :

$$ $$M_0 = \ left [\ vec {H} \ \ vec {G} \ \ vec {K} \ right] = \ left [\ begin {array} {cccc} H_x & 0 & H_y \\ H_y & 0 & -H_x \\ H_z & 1 & 0 \ end { matriz} \ right]$$

Del mismo modo, pero ya en cada iteración del bucle, se crea una matriz similar $$$M '= \ left [\ vec {h} \ \ vec {g} \ \ vec {k} \ right]$ donde $$$\ vec {h}$ Es el vector de inducción magnética normalizado actual, $$$\ vec {g}$ Es el vector de gravedad normalizado actual, $$$\ vec {k} = \ vec {h} \ times \ vec {g}$ . Esta matriz caracteriza la posición del LSC, porque Estos vectores son conocidos en el sistema de coordenadas de los sensores, que coincide con el LSC. Luego, conociendo ambas matrices, podemos escribir la siguiente ecuación:

$$ $$E'M '= E_0M_0$$

Vincula dos matrices encontradas en diferentes circunstancias. Dada una expresión $$$E '= CE_0$ y que base $$$E_0$ Es la matriz de identidad, obtenemos:

$$ $$CM '= M_0$$

Desde aquí expresamos la matriz de transición. $$$C$ :

$$ $$C = {\ left (M_0 ^ {- 1} \ right)} ^ TM '^ T$$

El primer factor, como puede comprender, se calcula solo una vez al comienzo del algoritmo, y no requiere un recuento en el proceso. El segundo factor se forma con bastante facilidad y no a la fuerza en cada iteración del ciclo.

Después, cuando se encuentra la matriz de transición, la transformamos en un cuaternión. $$$q_n ^ A$ (El algoritmo para convertir de una matriz a un cuaternión es algo público y no lo daré aquí).

Como resultado, sabemos que dos cuaterniones se encuentran independientemente uno del otro. Y para combinar los resultados, apliqué un filtro complementario simple con un coeficiente $$$F$ , que se toma del rango de 0 a 1:

$$ $$q_n = Fq_n ^ G + \ left (1-F \ right) q_n ^ A$$

Como resultado, obtenemos un cuaternión, que contiene información actualizada sobre la posición en el espacio del dispositivo con el módulo SINS.

La bicicleta funcionó ... El algoritmo funcionó, pero en algunas situaciones se comportó de manera inapropiada, lo que en principio no interfirió, pero no dio razones para pensar positivamente al respecto. Satisface mi interés deportivo, y ahora puedes recurrir a soluciones ya preparadas, mejor. Luego volví nuevamente al artículo de Sebastian Majwik y decidí usar su algoritmo, afortunadamente, de que esta maravillosa persona publicó todos los códigos fuente en el sitio web del proyecto . El archivo tenía códigos fuente en diferentes idiomas, incluido el lenguaje Matlab. Este hecho influyó en mi decisión de abandonar la idea de hacer todos los cálculos en el microcontrolador (especialmente porque es de 8 bits) y escribir el programa que ya está en la computadora en el entorno Matlab. El microcontrolador se usa solo para interrogar sensores y enviar datos a una PC (una situación similar con el manipulador). En este caso, el código del programa principal que sufre cambios y depuración se basa en el entorno Matlab, que es muy conveniente en el proceso.

Bueno, la orientación dada por el cuaternión que obtuvimos. ¿Qué sigue de acuerdo al plan? Y luego sigue las coordenadas lineales del objeto según el acelerómetro. Bueno, aquí es mejor decir simplemente que es imposible determinar las coordenadas usando el acelerómetro con la precisión necesaria. ¡Incluso al menos encuentre un cambio de posición que sea adecuado! Por supuesto, hubo intentos de resolver este problema, pero en tiempo real no fue posible encontrar las coordenadas. Por qué Porque la doble integración discreta de las lecturas ruidosas del sensor solo condujo a la estratosfera, y a una velocidad frenética, pero no a un resultado positivo. Por lo tanto, corté el algoritmo indicado al comienzo del párrafo hasta que se encontró la orientación, y me detuve allí.

3. Todo lo demás

Entonces, llegué a la etapa final del diseño, después de haber jugado lo suficiente con el manipulador y envolver el sensor IMU. Mientras trabajaba en los dos pasos anteriores, ya tenía una idea clara de cómo funcionaría todo y por qué algoritmo. Por lo tanto, lidié con esta etapa lo suficientemente rápido. Como solo se conoce la orientación de la palma, trabajamos directamente con el cuerpo de trabajo, que se requiere para orientarse en consecuencia. RO puede tomar cualquier dirección, si no viola el área de trabajo (rotar todo 360 no funciona).

En el ítem sobre el desarrollo del manipulador, el vector del PO se configuró manualmente, y luego se encontraron los ángulos de rotación de las unidades. Por lo tanto, este vector debe determinarse en función de la orientación de la palma de la mano. La orientación se puede expresar como base $$$E '$ encontrarlo convirtiendo el cuaternión en una matriz. La base consiste en vectores de columna de sus orths; por lo tanto, obtenemos tres vectores $$$\ vec {x} '$ , $$$\ vec {y} '$ y $$$\ vec {z} '$ . Será conveniente tomar el vector como orientación $$$\ vec {x} '$ , dado que asumí tal posición inicial del manipulador, cuando todos los enlaces y el PO están ubicados en el plano XZ del sistema de coordenadas base, y el PO es horizontal en ese momento, es decir vector $$$\ vec {v_0}$ Al principio, está alineado con el eje X del BSK y el NSC (colocamos la posición inicial del módulo SINS para que el NSC coincida con el BSK del manipulador). En este caso, la primera columna de la matriz $$$E '$ vector de igualación $$$\ vec {v_0}$ . Luego lo normalizamos a lo largo del PO y obtenemos el vector requerido relativo al sistema de coordenadas base del manipulador. Luego seguimos la secuencia de cálculo de coordenadas generalizadas de la p. 1.

Vale la pena señalar que el manipulador, al cambiar la orientación de la RO, es capaz de moverse en dos modos: el primero, cuando el punto de brida es estacionario, el segundo, cuando el punto final del PO es estacionario, pero se observa su orientación. El segundo modo es más interesante porque incluso en ausencia de movimiento lineal, todos los ejes de rotación todavía están involucrados para mover el punto de la brida, mientras se observa la orientación del PO. Sin embargo, la transición del primer modo al segundo ocurre con la adición de una sola operación de sustracción de vectores para encontrar el vector $$$\ vec {r}$ (ver párrafo 1)

Todas las operaciones anteriores también se programaron en el entorno de Matlab. En términos generales, la estructura del programa es la siguiente:

1. Calibración al inicio. Configuramos toda la granja en su posición original y, sin atrevernos a tocarla, calibramos el módulo SINS para una cierta cantidad de datos sin procesar. La calibración es necesaria, porque necesita eliminar el desplazamiento inicial que produjo el filtro (no entendía por qué, y funcionó bien).
2. El comienzo del guión. Inicializamos todas las bibliotecas y variables, establecemos la posición inicial de la brida o el punto final del PO.
3. Inicio de ciclo. En cada iteración, interrogamos a los sensores, encontramos el cuaternión, lo traducimos a una matriz, que es la base $$$E '$ , es la base en la que se encuentra el RO. La primera columna se toma como la orientación del PO y encontramos todas las coordenadas generalizadas utilizando las consideraciones matemáticas de la Sec. 1.
4. Conociendo las coordenadas generalizadas en el último momento y en el presente, calculamos la velocidad angular de rotación de los ejes.
5. Enviamos un paquete de datos al microcontrolador del manipulador.

Resultó, por supuesto, torpe, pero si observa más de cerca, puede ver un resultado positivo del estudio. Este trabajo, por supuesto, no pretende estar terminado y requiere mucho esfuerzo para refinar, pero solo si se puede usar. Pero aún no he encontrado una aplicación específica ... ¿Alguien puede decirme?