Hola Habr! En este artículo hablaré sobre la creación de un modelo matemático de una tubería larga para el programa CAE SimulationX en Modelica. Se tratará de calcular procesos de onda (pulsaciones de presión, golpe de ariete, etc.) en una línea hidráulica utilizando el método de características. A pesar de que este método es bastante antiguo, no hay suficiente información en RuNet sobre su aplicación para resolver problemas aplicados.

Debajo del corte, trataré de explicar por qué es necesario tener en cuenta los procesos de olas en las tuberías, para resaltar los problemas que encontré durante la programación y al final compararé el proceso de pulsación de presión cuando una bomba de agua de alta presión de tres émbolos opera en una tubería larga simple en el modelo y en el soporte URACA en Alemania

Introduccion

En la práctica de la ingeniería, por regla general, se presta poca atención a los procesos ondulatorios en tuberías. El ejemplo más famoso, cuando los procesos de olas estropean la vida de un ingeniero, es un golpe de ariete:



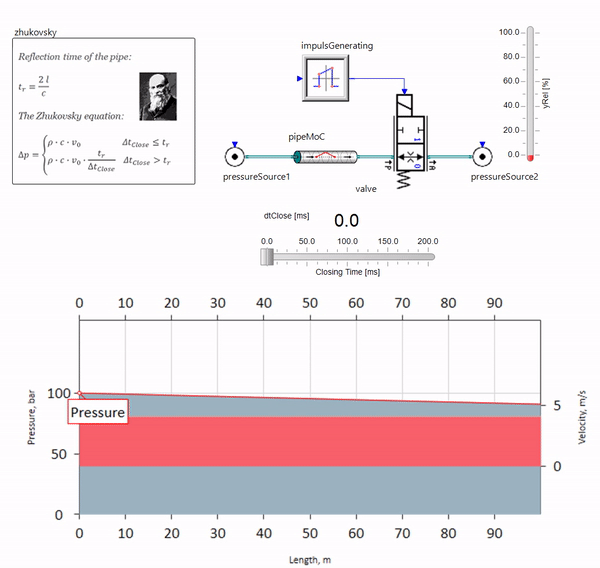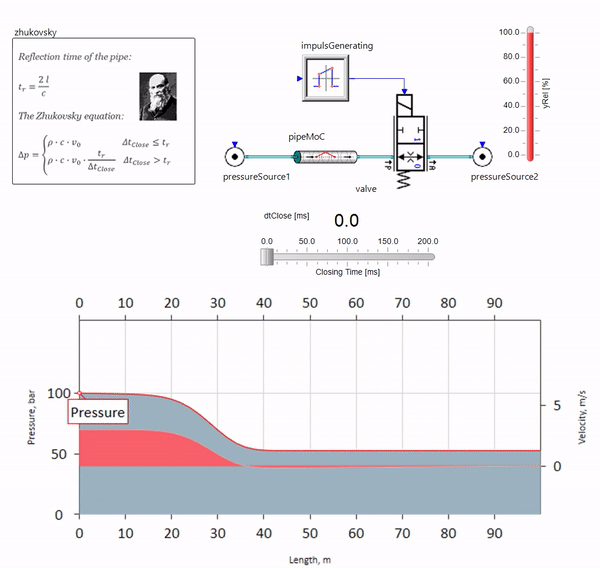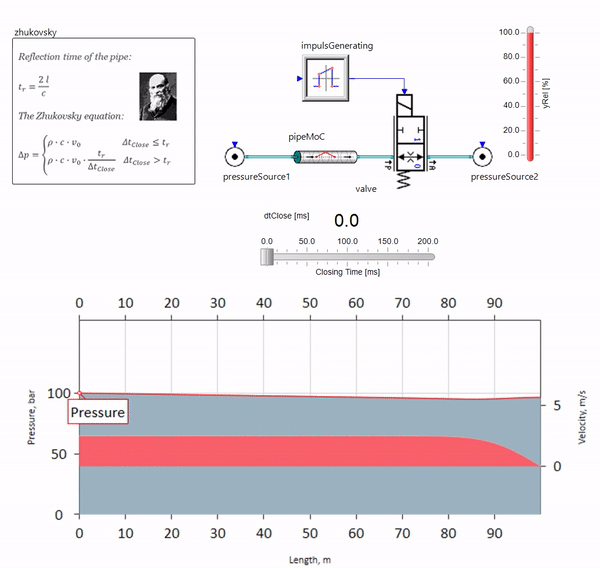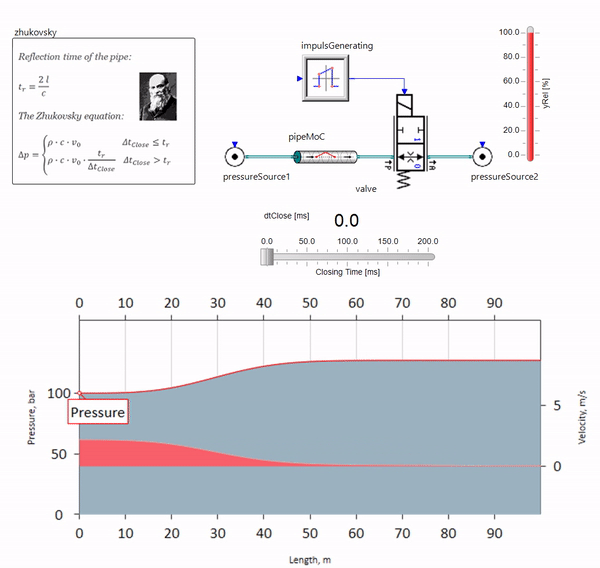
Cuando la válvula se cierra rápidamente al final de la tubería, aguas abajo, se produce una onda de presión que se mueve aguas arriba a la velocidad local del sonido (para el agua, aproximadamente 1,500 m / s), se refleja desde una fuente de presión constante, vuelve a la válvula y se refleja desde ella esta vez con un signo negativo. Este proceso se repite hasta que toda la energía se consume por fricción, y hasta entonces la válvula y toda la tubería están sujetas a cargas de choque, cuya amplitud y frecuencia dependen de la longitud de la tubería y la velocidad inicial del flujo del fluido.

Nikolai Zhukovsky describió el hidroblow con la precisión necesaria para resolver problemas prácticos a fines del siglo XIX, resolviendo así el problema de los accidentes en el suministro de agua de Moscú. Desde entonces, la fórmula para calcular el salto de presión cuando la válvula se cierra rápidamente se llama fórmula de Zhukovsky en todo el mundo:

$$

$$\ Delta p = \ rho \ cdot c \ cdot \ Delta v$$

El golpe de ariete en la práctica se manifiesta, como regla, con longitudes de tubería de cien metros. En las siguientes longitudes, ya es difícil encontrar equipos hidráulicos que puedan cerrarse más rápido que la onda de presión que pasa desde la válvula hacia atrás (la condición para la ocurrencia de un golpe de ariete). Sin embargo, incluso las tuberías relativamente cortas pueden arruinar la vida de los ingenieros si el sistema tiene una fuente de pulsaciones de flujo (por ejemplo, una bomba volumétrica con un número finito de émbolos).



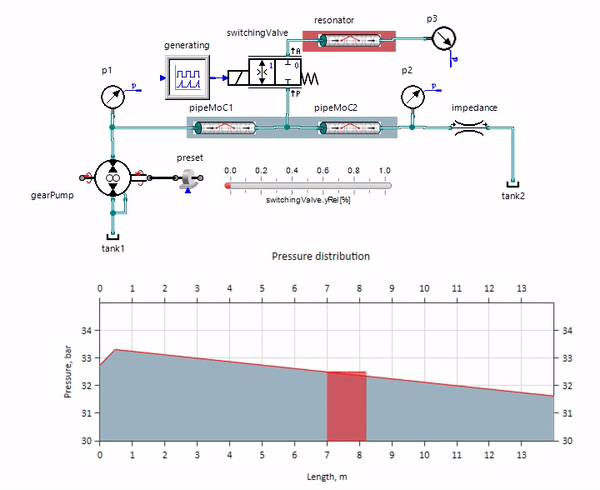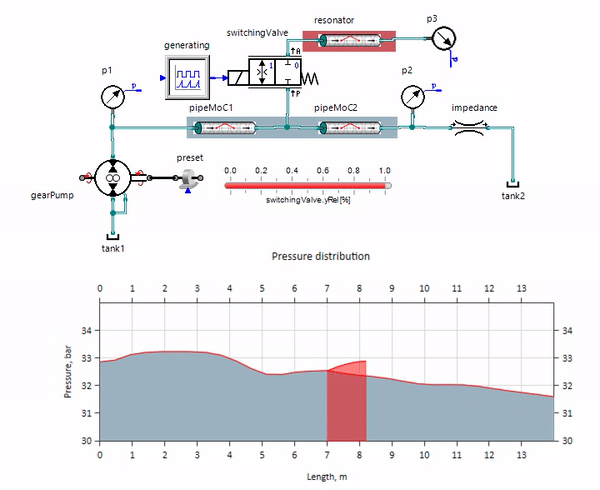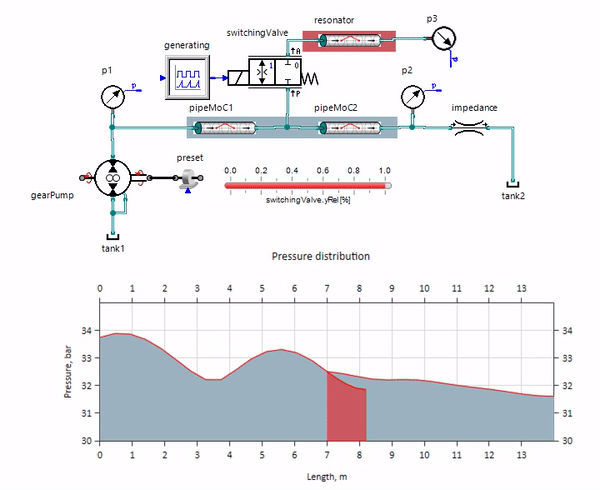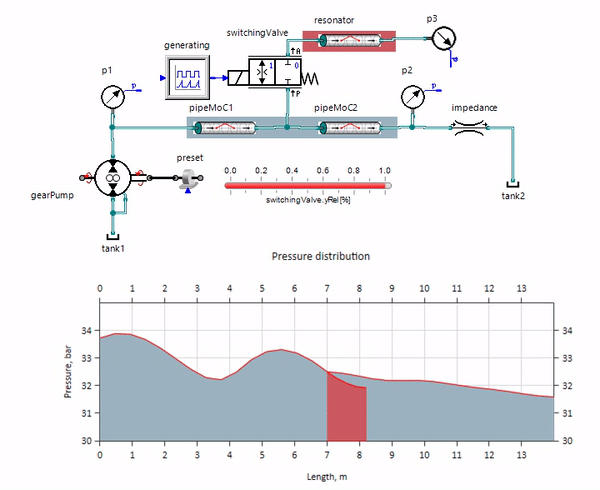
El gif muestra el efecto beneficioso de una tubería de poco más de un metro de largo. Su longitud es igual a un cuarto de la longitud de onda de la presión, por lo que cuando la conecta a la tubería principal, la llamada onda estacionaria, que en antifase golpea la fuente de las pulsaciones y las suprime de esta manera (este es el llamado amortiguador de pulsaciones de cuarto de onda). Está claro que con una desafortunada combinación de circunstancias, el efecto puede ser el contrario.

En mi práctica, intenté durante mucho tiempo descartar los procesos de onda, porque su cálculo requirió una comprensión más profunda de matan y métodos numéricos, que a lo largo de mis estudios traté con negligencia indulgente. Pero cuando un día vi con mis propios ojos que el consejo estándar (poner en todas partes un HPP, un acumulador hidráulico, organizar un respaldo en la entrada de la bomba) no ayuda a deshacerse de las pulsaciones en el banco, ni, además, acercarlos a comprender los procesos, tuve que profundizar en la alfombra. . Especialmente para mi vergüenza, mi supervisor de investigación ya ha comenzado a escribir un modelo de canalización en C ++ para mí.

1. Modelo unidimensional de una línea hidráulica en parámetros distribuidos.

El principal problema que hace que los modelos unidimensionales tradicionales descritos por las ecuaciones diferenciales ordinarias vayan más allá de la zona de confort es que la tubería más simple, incluso con los supuestos más atroces (está completamente llena de líquido, tiene una longitud transversal constante, la velocidad del fluido se promedia sobre la sección transversal, los procesos de transferencia de calor no son considerado) se describe mediante ecuaciones diferenciales en parámetros distribuidos (ecuaciones de Euler, solo teniendo en cuenta la fuerza de masa y la fricción en el lado derecho de la segunda avneniya):

$$

$$\ frac {\ partial \ rho} {\ partial t} + \ frac {\ partial (\ rho v)} {\ partial x} = 0,$$

$$

$$\ frac {\ partial (\ rho v)} {\ partial t} + \ frac {\ partial (\ rho v ^ 2 + p)} {\ partial x} = \ rho \ cdot (G + F),$$

donde $$$\ rho$- densidad $$$v$- velocidad $$$p$- presión $$$F$- pérdidas por fricción, $$$G$- caída de presión causada por la fuerza gravitacional.

Es decir integra ahora no solo necesitas a tiempo $$$t$pero también en coordenadas espaciales $$$x$.
En el caso de los líquidos, puede simplificar su vida un poco más si reescribe las ecuaciones de variables conservadoras a variables primitivas (velocidad y presión):

$$

$$\ frac {\ partial p} {\ partial t} + v \ frac {\ displaystyle \ partial p} {\ displaystyle \ partial x} + \ rho \; c ^ 2 \ frac {\ partial v} {\ partial x } = 0$$

$$

$$\ frac {\ partial v} {\ partial t} + \ frac1 \ rho \ frac {\ displaystyle \ partial p} {\ displaystyle \ partial x} + v \ frac {\ displaystyle \ partial v} {\ displaystyle \ partial x} = F + G$$

donde $$$c$- velocidad del sonido.

Ahora, si aceptamos que la velocidad del sonido es significativamente mayor que la velocidad del movimiento del fluido $$$v \ ll c$(lo cual es cierto en ausencia de cavitación), las ecuaciones serán aún más simples:

$$

$$\ frac {\ partial p} {\ partial t} + \ rho \; c ^ 2 \ frac {\ partial v} {\ partial x} = 0$$

$$

$$\ frac {\ partial v} {\ partial t} + \ frac1 \ rho \ frac {\ displaystyle \ partial p} {\ displaystyle \ partial x} = F + G$$

Para resolver estas ecuaciones, de una forma u otra, elimine la diferenciación en coordenadas espaciales $$$x$. Esto se puede hacer de frente si reemplaza el diferencial espacial con un esquema de diferencia finita, y en el caso del tiempo, simplemente vaya al diferencial completo, diciendo que dentro de la misma celda, los parámetros de estado no dependen de la coordenada:

$$

$$\ frac {dp} {dt} = - \ rho \; c ^ 2 \ frac {\ triangle v} {\ triangle x}$$

$$

$$\ frac {dv} {dt} = F + G- \ frac1 \ rho \ frac {\ displaystyle \ triangle p} {\ displaystyle \ triangle x}$$

Ahora estas ecuaciones se pueden resolver como ecuaciones diferenciales ordinarias, dividiendo la longitud de la tubería en muchos volúmenes finitos. Entonces, esto se hace , por ejemplo, en el paquete Simscape, en MATLAB Simulink, y así el problema se resolvió hasta hace poco en SimulationX .
Por supuesto, se puede calcular algo de esta manera, pero las fluctuaciones numéricas que surgen en este caso se ven muy obstaculizadas:

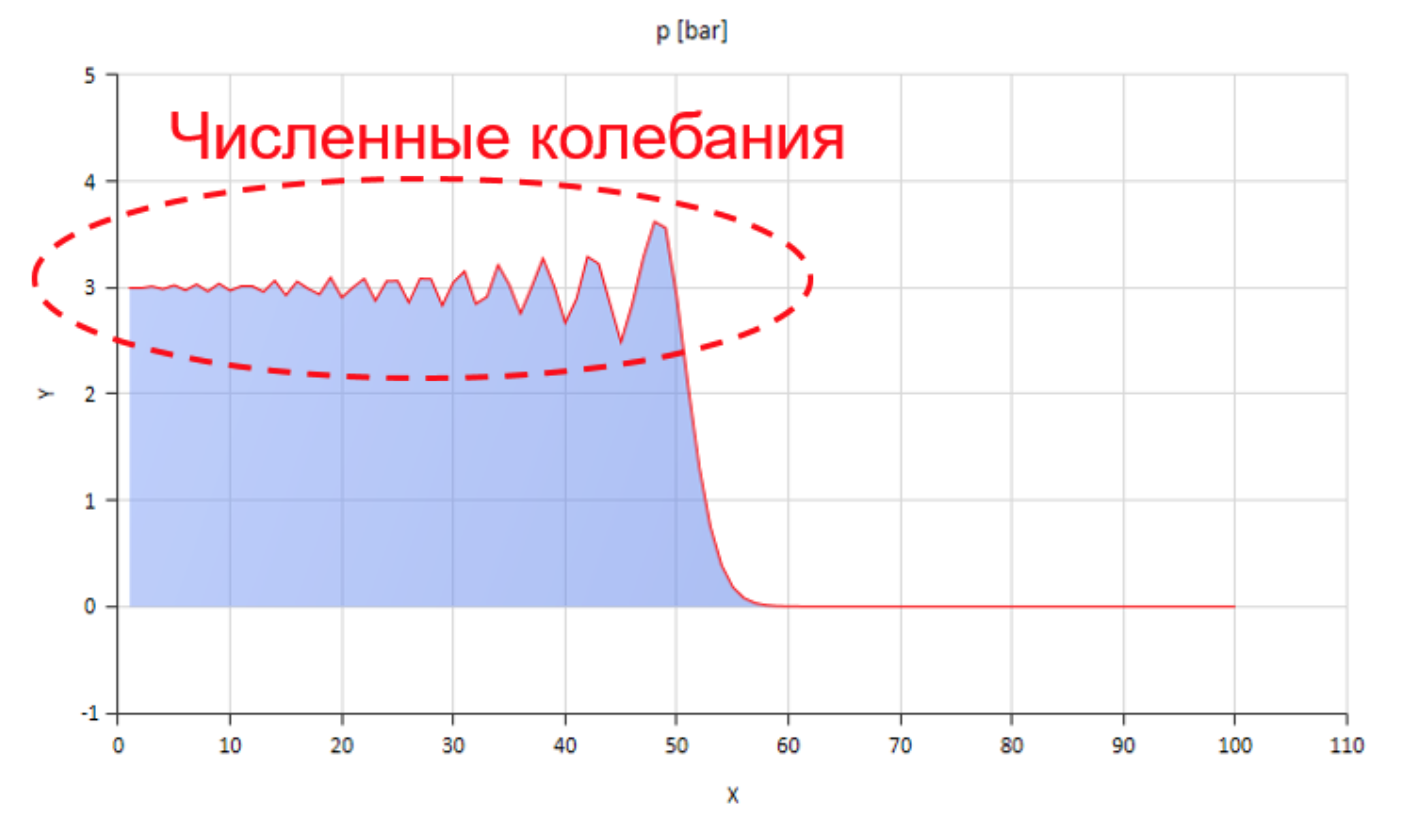La figura muestra el frente de la onda de presión moviéndose de izquierda a derecha.

Puede lidiar con estas oscilaciones, por ejemplo, introduciendo difusión numérica, pero luego la velocidad de propagación de la onda se distorsiona significativamente. Puede aumentar la fricción (especialmente ayudando a aumentar su componente no estacionario), pero luego el modelo deja de reflejar la esencia física.

Es mejor utilizar un método diferente para transformar ecuaciones en parámetros distribuidos en ecuaciones diferenciales ordinarias, por ejemplo, el método de características.

2. Método de caracterización

Wikipedia recomienda "Método de características" recomienda:

... para encontrar características a lo largo de las cuales la ecuación diferencial parcial se convierte en una ecuación diferencial ordinaria. Tan pronto como se encuentran las ecuaciones diferenciales ordinarias, se pueden resolver a lo largo de las características y la solución encontrada se puede convertir en una solución de la ecuación diferencial parcial original.

Es como la piedra filosofal, pero en lugar de convertir metales en oro, convertimos las ecuaciones diferenciales parciales en ordinarias, y viceversa. Surge la pregunta: "¿cómo aplicar esto en la práctica?", Y preferiblemente más efectivamente que los alquimistas medievales ...

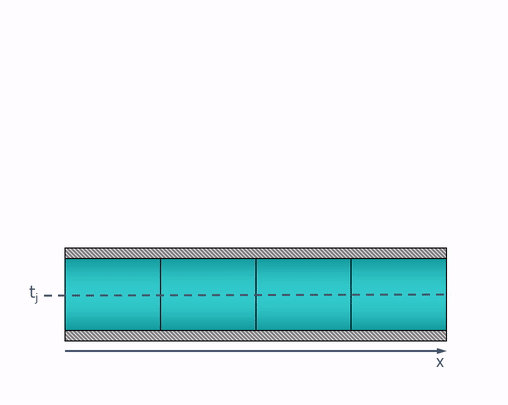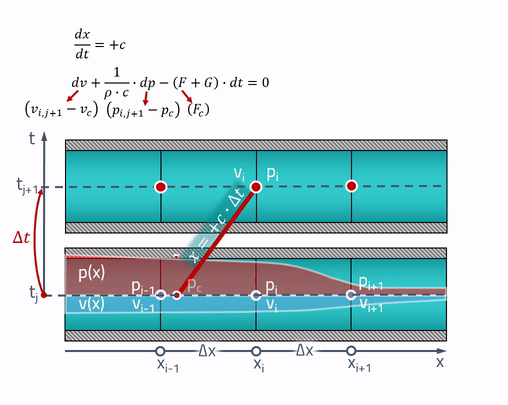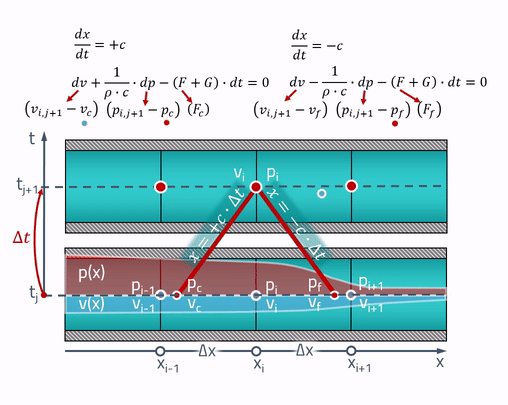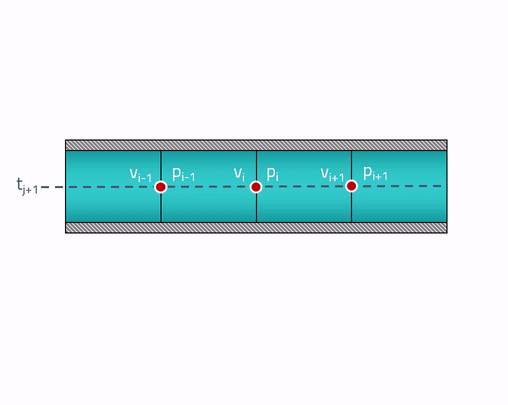
Para empezar, entenderemos el enunciado del problema. En nuestro momento inicial de tiempo, tenemos algún tipo de distribución de presiones y velocidades a lo largo de la tubería. Primero, dividimos la tubería en un número finito de elementos y asignamos un valor de presión a cada cara $$$p_i$y velocidad $$$v_i$.


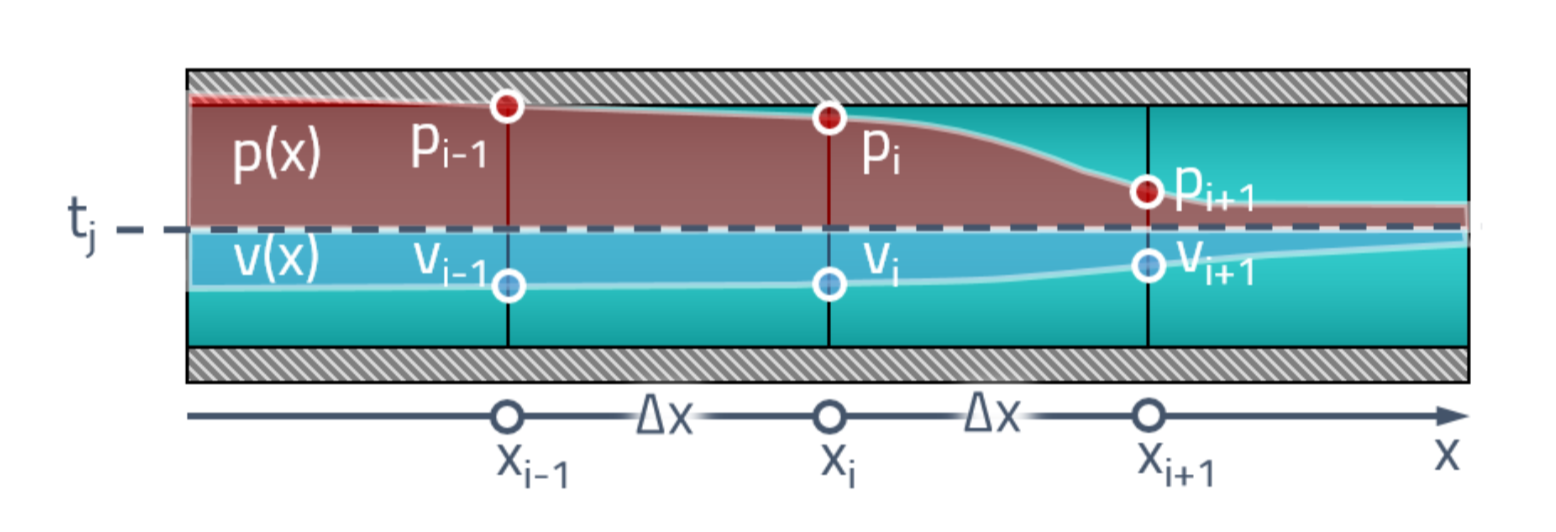
Estamos interesados ​​en cómo cambian los valores en estos puntos con el tiempo $$$\ triangle t$. Avance rápidamente al espacio-tiempo y coloque el estado de la tubería en el futuro por encima del estado inicial:



¡Aquí es donde las características "mágicas" son útiles! La explicación campesina de trabajo es que todos los cambios en la tubería ocurren a la velocidad del sonido. Presión y velocidad en el momento actual. $$$i$dependerá de la presión y la velocidad en esos puntos de la tubería donde estaba la onda de sonido (sería) $$$\ triangle t$hace segundos Esto se ilustra de la siguiente manera:



Se dibujan dos líneas simétricas desde cualquier punto, cuya pendiente está determinada por la velocidad del sonido. Estas son las características a lo largo de las cuales las ecuaciones diferenciales parciales se convierten en ecuaciones diferenciales ordinarias. Si nombramos los puntos en los que las características se cruzan con el estado de la tubería en el pasado como $$$c$y $$$f$, las ecuaciones se escriben de la siguiente manera:

$$

$$dv + \ frac1 {\ rho c} dp- (F + G) dt = 0 \; for \; \ frac {dx} {dt} = + c$$

$$

$$dv- \ frac1 {\ rho c} dp- (F + G) dt = 0 \; for \; \ frac {dx} {dt} = - c$$

Los valores de presiones y velocidades en estos puntos se pueden obtener por interpolación lineal entre los valores de los parámetros de estado en la cuadrícula:


¡Es importante tener en cuenta que estos puntos siempre deben estar dentro de las celdas vecinas! Para esto, el paso de tiempo debe satisfacer el criterio de Courant - Friedrichs - Levy (CFL):

$$

$$\ triangle t <\ frac {\ triangle x} c$$

Ahora, al menos el esquema de diferencia más simple se puede aplicar a estas ecuaciones:

$$

$$(v_ {i, \; j + 1} -v_c) + \ frac1 {\ rho c} (p_ {i, \; j + 1} -p_c) - (F + G) \ triangulo t = 0$$

$$

$$(v_ {i, \; j + 1} -v_f) - \ frac1 {\ rho c} (p_ {i, \; j + 1} -p_f) - (F + G) \ triangulo t = 0$$

En el sistema resultante de dos ecuaciones, dos incógnitas: presión $$$p_ {i, \; j + 1}$y velocidad $$$v_ {i, \; j + 1}$. Puede resolverlo numéricamente, pero no hay ningún problema particular para obtener una solución analítica. Luego, si aceptamos la constancia de la velocidad del sonido, obtenemos un esquema de diferencia completamente explícito.

Para consolidar, daré una animación del método de características:

3. Experimento

Tuve la oportunidad de recordar finalmente el modelo cuando comencé a trabajar en ESI ITI GmbH en Dresden. Una vez, recibí un boleto en Helpdesk, donde los ingenieros de URACA se quejaron de que no podían lograr la convergencia con el experimento con nuestra tubería "vieja".
Fabrican bombas de émbolo de agua a alta presión, un enorme "Karcher", y les gustaría poder predecir posibles efectos resonantes debido a la inclusión Procesos de onda en la tubería. El problema es que tales bombas, como regla, tienen muy pocos émbolos y funcionan a bajas velocidades (250-500 rpm):



Debido a esto, y también debido a la influencia de la compresibilidad del líquido, el flujo de salida es muy desigual:



Las brechas y las no linealidades dificultan la linealización y el análisis del modelo en el dominio de la frecuencia, y los cálculos de CFD para tal tarea se disparan desde un cañón a los gorriones. Además, ya tenían modelos en SimulationX, donde tenían en cuenta la dinámica de la parte mecánica de la bomba, la elasticidad del bastidor y las características del motor eléctrico, por lo que sería interesante ver cómo la tubería afecta esto.

El diseño del banco de pruebas es bastante simple:



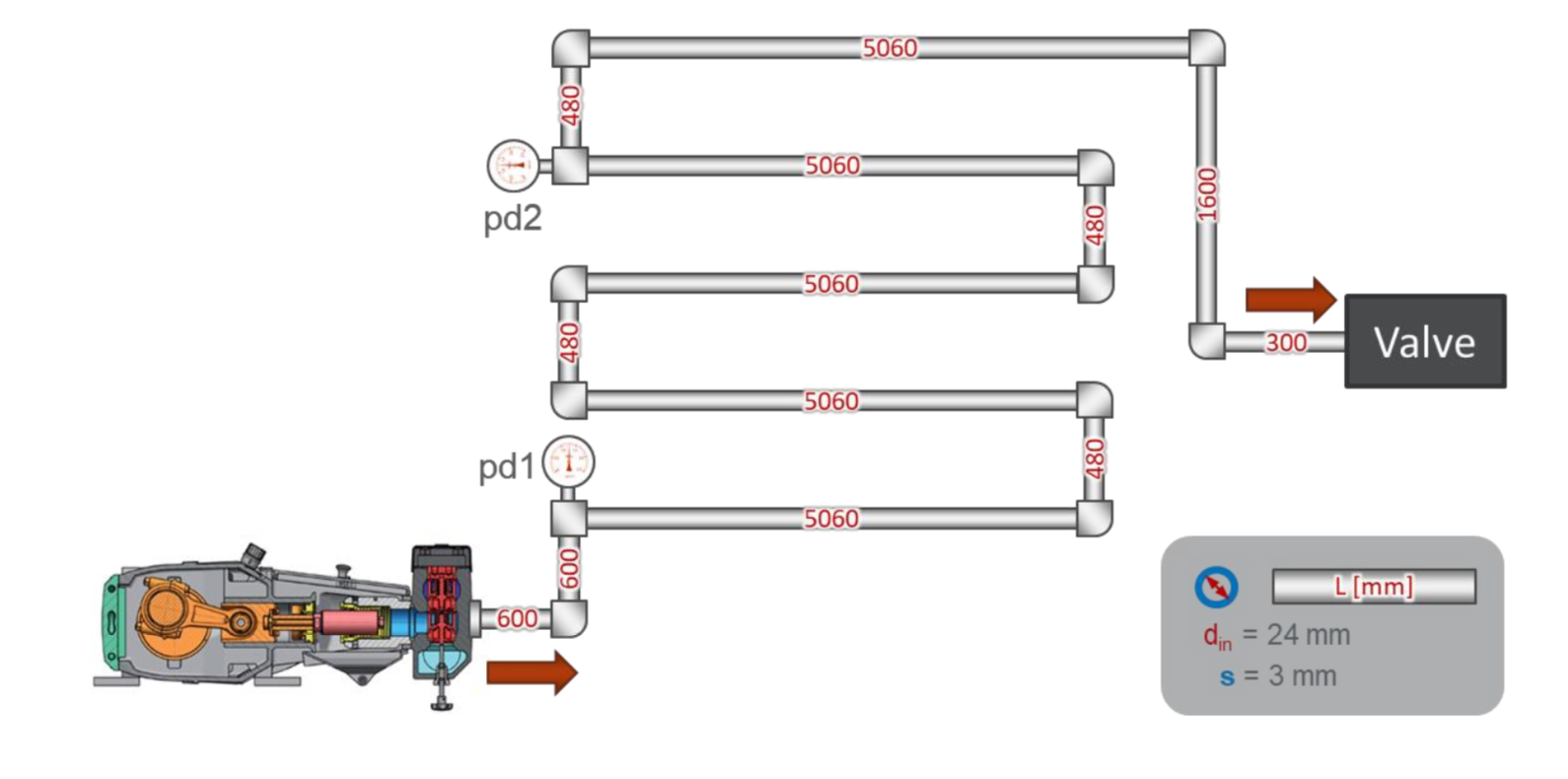
Hay una tubería simple con una longitud total de aproximadamente 30 metros. Al comienzo de la tubería, se instala un sensor de presión pd1, a una distancia de 22 metros, un sensor de presión pd2. Al final de la tubería hay una válvula que ajusta la presión en el sistema.

Sugerí probar la versión beta de mi modelo, como resultado de que dicho modelo fue construido en SimulationX:



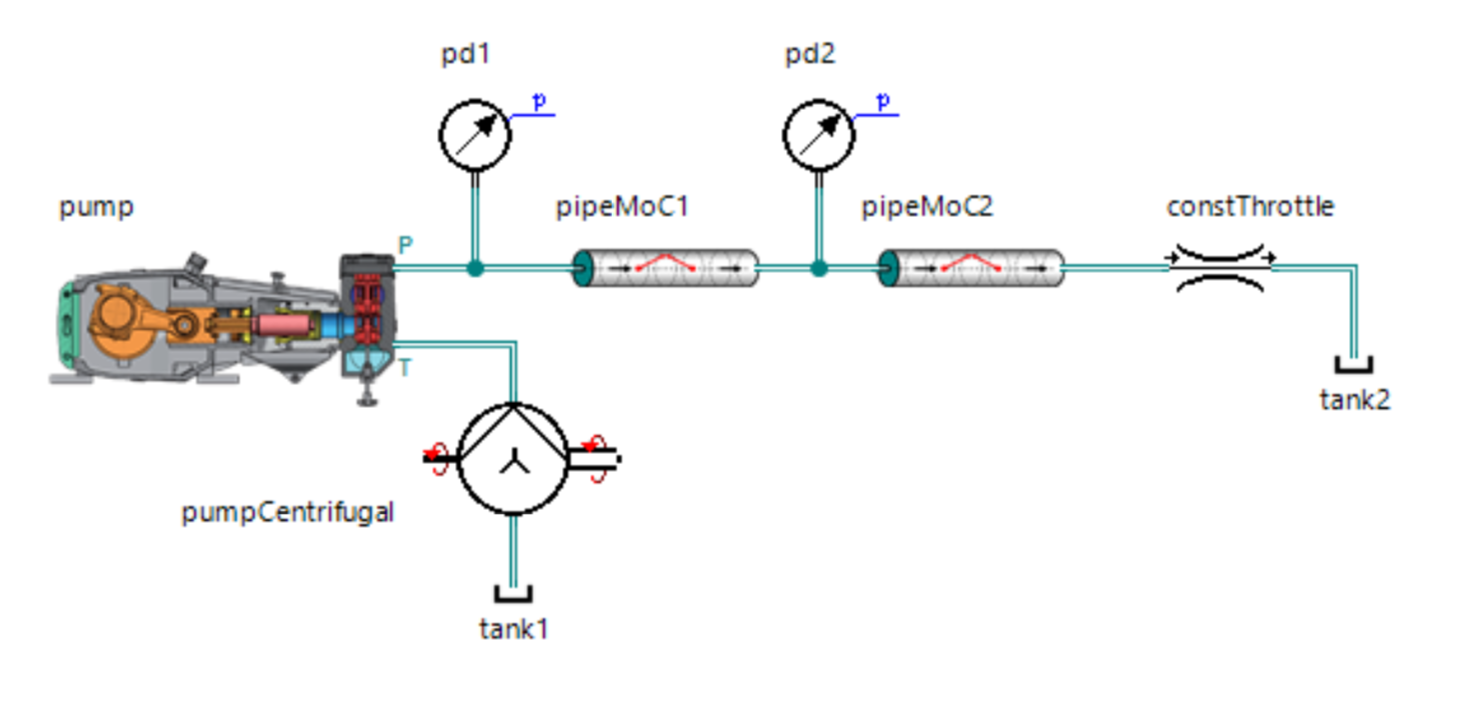
Los resultados incluso me sorprendieron gratamente:




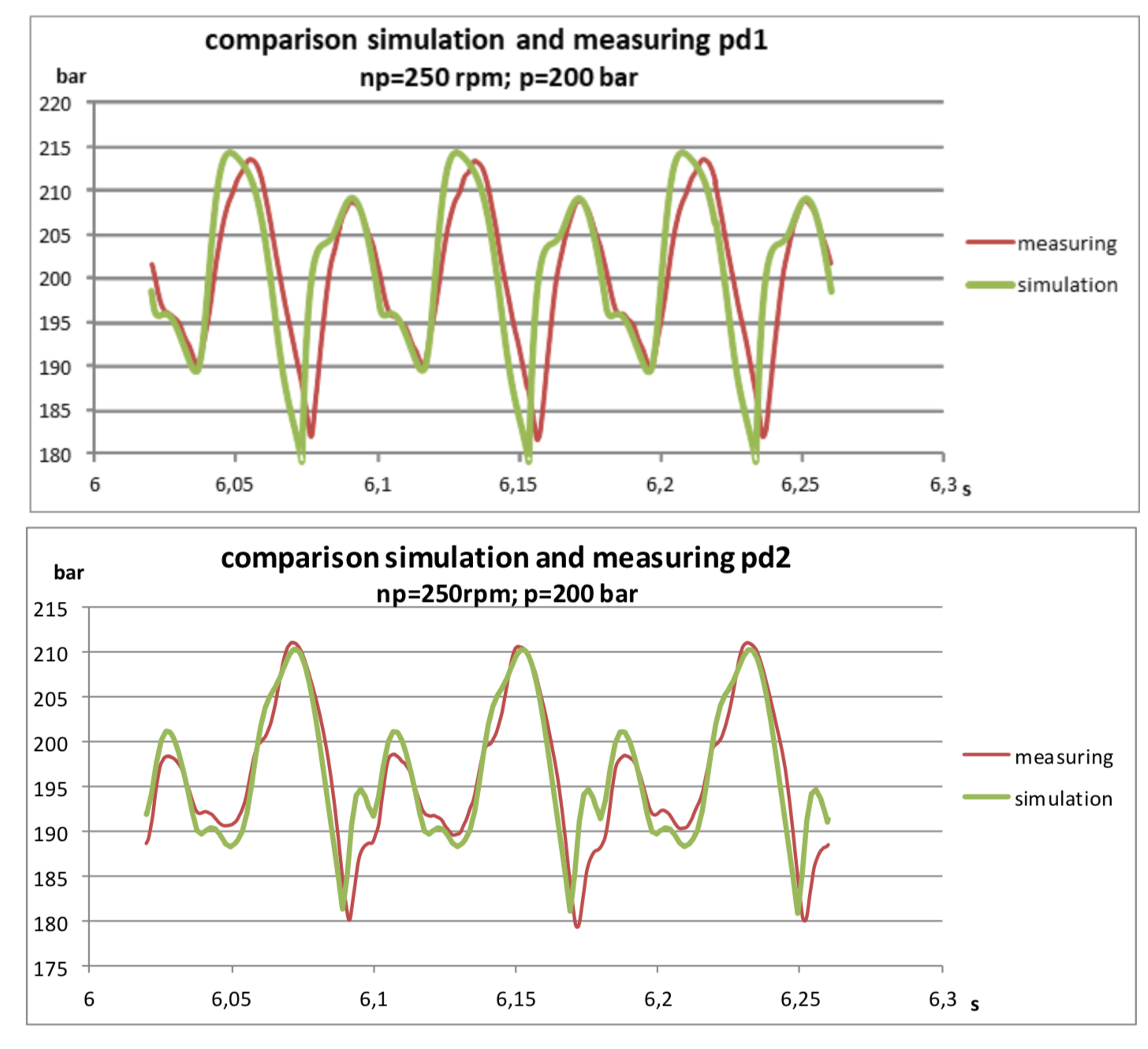
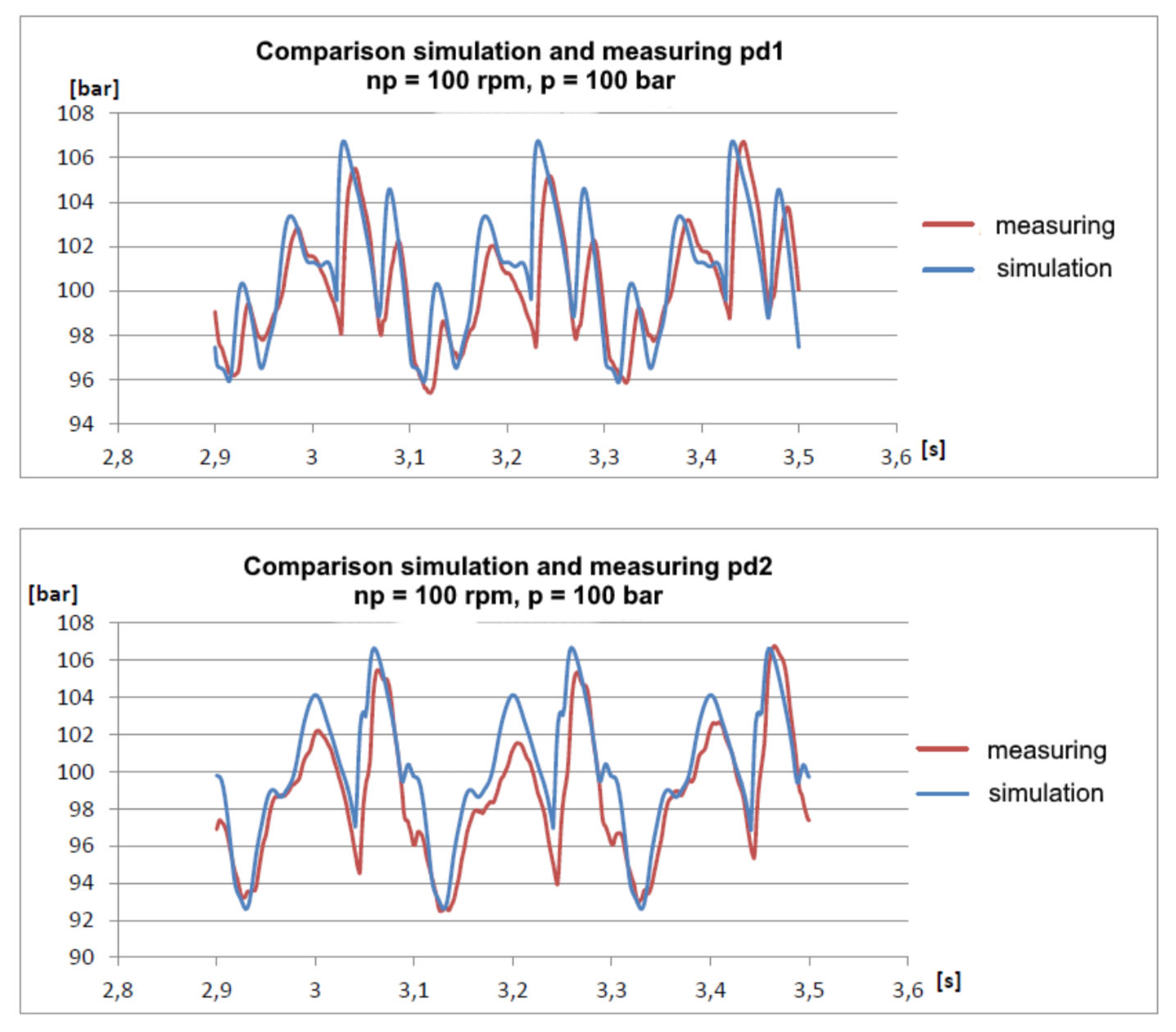
Se puede ver que el modelo está ligeramente amortiguado, lo cual es comprensible siempre que no tenga en cuenta la resistencia hidráulica. Sin embargo, los armónicos fundamentales son bastante buenos en coincidencia y permiten predecir amplitudes de presión con bastante buena precisión.

Esta experiencia me permitió lanzar rápidamente un nuevo modelo de la línea hidráulica en el lanzamiento de SimulationX, y me sumergí en este tema y no noté cómo, junto con el estudiante interno, también vi el modelo de la línea neumática, donde todo era mucho más interesante. Allí, tuve que usar un método basado en el método Godunov, que a su vez se basa en la solución del problema de Riemann de descomposición de una discontinuidad arbitraria, pero ¿qué pasa con esto en otro momento ...

Literatura

1. En la literatura nacional, el método de características para aplicaciones de ingeniería se describe mejor en el libro "Hidromecánica", D. N. Popov, S. S. Panaiotti, M. V. Riabinina
2. En su publicación
   Simulación de tubería por el método de características para calcular la pulsación de presión de una bomba de émbolo de agua de alta presión

   "Dr.-Ing. (Rus) Maxim Andreev, Dipl.-Ing. Uwe Grätz y Dipl.-Ing. (FH) Achim Lamparter ”, 11ª Conferencia Internacional de Energía Fluida, 11. IFK, 19-21 de marzo de 2018, Aquisgrán, Alemania, consulte el texto en PM
   Examiné con más detalle los problemas de acoplar el método de características y el solucionador del ODE.
3. Quién tiene acceso a las bibliotecas alemanas, la mejor visión general de los métodos para resolver ecuaciones hiperbólicas aplicadas a las líneas hidráulicas que he conocido se encuentra en la siguiente disertación: Beck, M., Modellierung und Simulation der Wellenbewegung en kavitierenden Hydraulikleitungen, Univ. Stuttgart, Alemania, 2003.
4. Clásicos del género de ecuaciones hiperbólicas en general: Randall J. Leveque, Métodos de volumen finito para problemas hiperbólicos, Cambridge University Press, Cambridge, Reino Unido, 2002.