Programación dinámica en problemas olímpicos

Hola

Recientemente resolví problemas del archivo Timus Online Judge y encontré una sección llamada tareas de programación dinámica . Este tipo de tarea es de particular interés para mí, porque a menudo este enfoque garantiza la velocidad y la elegancia de la solución. ¿Qué es la programación dinámica?

La programación dinámica es un enfoque para resolver problemas en el que hay una división en subtareas que son "más simples" en comparación con la original. La palabra "dinámico" tiene un significado cercano a "inductivo": se supone que la respuesta se conoce por algún significado $$$k$, y quiero encontrar la respuesta para $$$k + 1$. En matemáticas, esto se llama transición inductiva y es la idea principal de la programación dinámica.

Ejemplos simples

La tarea más llamativa e indicativa es la tarea de computación $$$n$número de la secuencia de Fibonacci. Se sabe que la secuencia tiene las siguientes propiedades:

$$

$$F_0 = F_1 = 1, \ F_n = F_ {n-1} + F_ {n-2}.$$

Esto implica inmediatamente la fórmula de recurrencia:

int Fibonacci(int n) { if(n == 1 || n == 2) return 1; return Fibonacci(n-1) + Fibonacci(n-2); } 

Si la recursión está buscando un número "desde el final", entonces el siguiente método calcula secuencialmente todos los números ubicados entre $$$0$y $$$n$:

 int dpFibonacci(int n) { int prev1 = 1; int prev2 = 1; int curr = 0; for(int j = 2; j < n; j++) { curr = prev1 + prev2; prev1 = prev2; prev2 = curr; } return curr; } 

Está claro que para lo suficientemente grande $$$n$Este algoritmo funciona mucho más rápido: no calcula valores intermedios varias veces. Considere un ejemplo un poco más complejo.

Ejemplo 1. Estás caminando por una escalera de peaje. Pisar $$$i$paso tienes que pagar $$$a_i$monedas Puede pasar al siguiente paso o saltar sobre uno. Tarea: pasar $$$n$pasos y gastar la menor cantidad de monedas posible.

Está claro que al pasar por cada paso, minimizamos el número de "pagos", pero podemos encontrar un paso muy costoso, que nos gustaría evitar. Crea una matriz de valores $$$d$en el cual en $$$j$-el puesto será el número (mínimo) de monedas que se deben gastar para llegar a $$$j$paso Está claro de inmediato que $$$d_1 = a_1, \ d_2 = a_2$. Y luego tomaremos un mínimo de los dos pasos anteriores y agregaremos el costo del paso en sí:

$$

$$d_i = \ min \ left (d_ {i-1}, d_ {i-2} \ right) + a_ {i}.$$

Cambiamos un poco las condiciones del problema: supongamos que en algunos pasos puede obtener monedas (esto significará que $$$a_k <0$) ¿Qué hay que cambiar en el algoritmo para que dé el resultado correcto?


Considere otro ejemplo que utiliza dinámicas "bidimensionales".

Ejemplo 2. En el laberinto hay $$$n \ veces m$habitaciones, cada una de las cuales contiene oro (en una jaula $$$(i, j)$mentiras $$$a_ {ij}$oro). La tarea es determinar qué cantidad máxima de oro se puede recolectar con una ruta óptima desde un punto $$$(0,0)$hasta el punto $$$(n, m)$si puedes ir hacia abajo o hacia la derecha.

Entonces, queremos saber la mejor ruta a la celda $$$(i, j)$. Podemos llegar aquí desde dos celdas: $$$(i-1, j)$y $$$(i, j-1)$. Dado que se conocen las rutas óptimas para estas dos celdas (se almacenan en alguna tabla $$$d$), entonces la respuesta para la celda $$$(i, j)$obtenido de la siguiente manera:

$$

$$d_ {ij} = \ max \ left (d_ {i-1j}, d_ {ij-1} \ right) + a_ {ij}.$$

Esta es otra tarea de programación dinámica clásica, cuyas modificaciones son bastante comunes en las tareas de programación deportiva. Una tarea similar se explica con más detalle aquí .

Tareas más desafiantes

Si lo desea, se puede atornillar un enfoque dinámico donde lo desee. Considere una tarea del archivo Timus Online Judge.

La formulación matemática del problema es la siguiente: se requiere encontrar el número mínimo de términos necesarios para descomponer un número dado en cuadrados completos.

Como antes, supongamos que sabemos las respuestas para todos los números. $$$k-1$que se almacenan en alguna matriz $$$d$y nos gustaría encontrar $$$d_ {k}$.

Toma este número $$$k$y analizar qué situaciones pueden ser:

1. $$$k$Es una plaza llena. En este caso $$$d_ {k} = 1$.
2. Quizás el número anterior $$$k-1$Era un cuadrado completo. Entonces $$$d_ {k} = d_ {k-1} + 1$.

En general, la opción de agregar una unidad a la anterior no parece tan mala.

Procedemos de la siguiente manera: buscamos una descomposición $$$k = q ^ 2 + s$tal que

$$

$$d_ {q ^ 2} + d_s <d_ {k-1} + 1.$$

Desde $$$q ^ 2$- plaza completa entonces $$$d_ {q ^ 2} = 1$y

$$

$$d_s <d_ {k-1},$$

es decir, encontramos una partición que es simplemente mejor que $$$d_ {k-1} + 1$, y la respuesta en este caso será

$$

$$d_k = d_ {s} + d_ {q ^ 2} = d_s + 1.$$

Considere el siguiente problema . El objetivo es construir una escalera desde $$$N$cubos según las reglas:

1. la escalera tiene al menos dos escalones;
2. una escalera no puede tener dos escalones idénticos;
3. los escalones de las escaleras van en orden ascendente (es decir, el siguiente es más grande que el anterior).

Esta vez construiremos dinámicas bidimensionales. Crear una tabla $$$d$en el que el puesto $$$(i, j)$el número de escaleras que consiste en $$$i$cubos cuya altura no exceda $$$j$. Si funciona, la respuesta a nuestro problema será la suma.

$$

$$\ sum \ limits_ {j = 1} ^ n d_ {nj}.$$

Entonces, resolveremos el problema de encontrar el número de escaleras compuesto por $$$i$cubos que son altos $$$j$. La imagen muestra las escaleras que caen en $$$d_ {74}$:

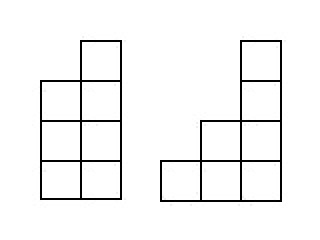
Como conocemos todas las escaleras, que consisten en menos cubos, las dividiremos. $$$(i, j)$columna derecha El resultado es una escalera c $$$i-j$cubos Ejemplo para $$$i = 9, \ j = 4$:

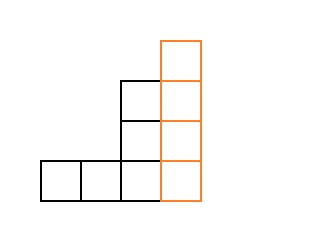
Pero para tales escaleras, el resultado ya se conoce, por lo que clasificaremos todas esas escaleras con un ciclo en $$$k$y sumar todos los resultados. De esta manera

$$

$$d_ {ij} = \ sum \ limits_ {k = 1} ^ {j-1} d_ {i-jk}.$$

Ahora clasificaremos las alturas de las escaleras:

$$

$$d_ {ij} = \ sum \ limits_ {k = 1} ^ {j-1} d_ {i-jk}, \ j = \ overline {1, i}.$$

Finalmente cambiando $$$i$de $$$1$antes $$$n$Obtenemos la respuesta.

Importante : en el proceso de construcción de nuestra matriz, es necesario considerar $$$d_ {ii} = 1$, ya que de lo contrario algunos tipos de escaleras se “perderán” (cuando se “separen”), pero no hace falta decir que dicha escalera no satisface las condiciones del problema, por lo que la respuesta será el número $$$d_ {nn} - 1$.


La siguiente tarea se resuelve utilizando una matriz unidimensional.

Entonces lo que tenemos. El primero ent sabe 2 palabras. Cada ent enseña todas las palabras que él mismo conoce dos ents: jóvenes y viejos. A su vez, a los jóvenes se les enseñaron tantas palabras como él ya sabe, y al viejo solo se le enseñó una palabra. Necesitas saber cuántos ents saben exactamente $$$K$palabras (es necesario deducir el número de estos módulos ents $$$P$)

La solución es bastante simple. Crea una matriz $$$d$en el cual en $$$i$-º lugar almacenaremos el número de ents (módulo $$$P$) quien sabe $$$i$palabras Todo comienza con el primer ent, que conoce dos palabras, por lo tanto $$$d_2 = 1$. Y luego todo es simple:

• Todos los entrantes que conocen un número impar de palabras son viejos y solo pudieron aprender de los anteriores. Por lo tanto para impar $$$i: \ d_i = d_ {i-1};$
• En cuanto a los entrantes que saben un número par de palabras, estos son todos aquellos que recibieron la misma cantidad de palabras de los elfos (jóvenes) $$$+$aquellos que han aprendido de lo anterior (antiguo); es decir, incluso $$$i$tenemos $$$d_i = d _ {{i \ barra invertida 2}} + d_ {i-1}$.

Queda por tratar con el módulo de cálculo. Para no almacenar grandes cantidades, recordaremos de inmediato todos los módulos de valores.


Recursos utilizados:

1. Timus Juez en línea;
2. Un poco sobre programación dinámica;
3. Propiedades de comparación módulo.