Introduccion
La ecuación de tipo elíptico más común es la ecuación de Poisson.
Muchos problemas de física matemática se reducen a la solución de esta ecuación, por ejemplo, los problemas de la distribución de temperatura estacionaria en un sólido, problemas de difusión, los problemas de distribución del campo electrostático en un medio no conductor en presencia de cargas eléctricas, y muchos otros.
Para resolver ecuaciones elípticas en el caso de varias mediciones, se utilizan métodos numéricos para convertir ecuaciones diferenciales o sus sistemas en sistemas de ecuaciones algebraicas. La precisión de la solución está determinada por el paso de la cuadrícula de coordenadas, el número de iteraciones y la cuadrícula de bits de la computadora [1]
El propósito de la publicación es obtener una solución a la ecuación de Poisson para las condiciones de contorno de Dirichlet y Neumann, para investigar la convergencia del método de solución de relajación utilizando ejemplos.
La ecuación de Poisson se refiere a ecuaciones de tipo elíptico y en el caso unidimensional tiene la forma [1]:
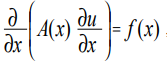
(1)
donde x es la coordenada; u (x) es la función deseada; A (x), f (x) son algunas funciones de coordenadas continuas.
Resolvemos la ecuación de Poisson unidimensional para el caso A = 1, que en este caso toma la forma:
(2)
En el intervalo [xmin, xmax] definimos una cuadrícula de coordenadas uniforme con un paso Δ:
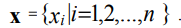
(3)
Las condiciones de contorno del primer tipo (condiciones de Dirichlet) para el problema considerado pueden representarse como:
(4)
donde x1, xn son las coordenadas de los puntos límite de la región [xmin, xmax]; g1, g2 - algunos
constantes
Las condiciones de contorno del segundo tipo (condiciones de Neumann) para el problema considerado pueden representarse como:
(5)
Discretizando las condiciones de contorno de Dirichlet en una cuadrícula de coordenadas uniforme (3) usando el método de diferencia finita, obtenemos:
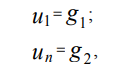
(6)
donde u1, un son los valores de la función u (x) en los puntos x1, xn, respectivamente.
Discretizando las condiciones de contorno de Neumann en la cuadrícula (3), obtenemos:
(7)
Discretizando la ecuación (2) para los puntos internos de la cuadrícula, obtenemos:
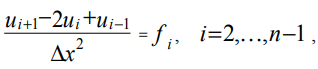
(8)
donde ui, fi son los valores de las funciones u (x), f (x) en el punto de la cuadrícula con la coordenada xi.
Por lo tanto, como resultado de la discretización, obtenemos un sistema de ecuaciones algebraicas lineales de dimensión n que contiene n - 2 ecuaciones de la forma (8) para puntos internos de la región y ecuaciones (6) y (7) para dos puntos límite [1].
La siguiente es una lista de Python de una solución numérica a la ecuación (2) con condiciones de contorno (4) - (5) en la cuadrícula (3).
Solución de listadofrom numpy import* from numpy.linalg import solve import matplotlib.pyplot as plt x0=0
Obtenemos:
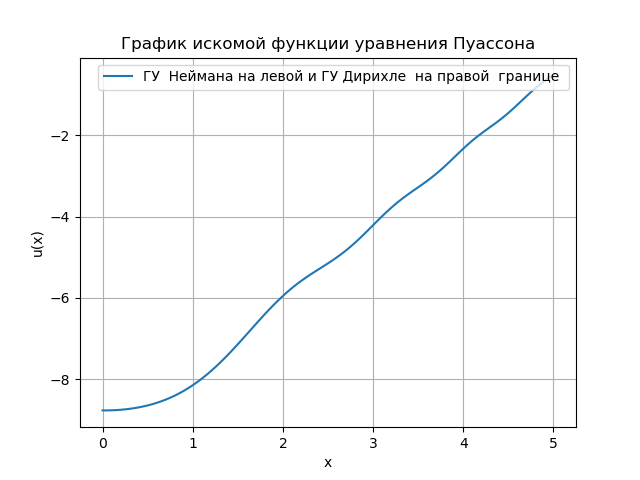
El programa que desarrollé en Python es conveniente para analizar las condiciones de contorno. El algoritmo de solución de Python anterior utiliza la función Numpy - u = linalg.solve (a, bT) .T para resolver un sistema de ecuaciones algebraicas, lo que aumenta la velocidad con la matriz cuadrada {a}. Sin embargo, con un aumento en el número de mediciones, es necesario cambiar al uso de tres matrices diagonales, cuya solución es complicada incluso para una tarea muy simple, encontré un ejemplo en el foro:
Ejemplo de una solución con matriz de tres diagonales. from __future__ import print_function from __future__ import division import numpy as np import time ti = time.clock() m = 1000 A = np.zeros((m, m)) B = np.zeros((m, 1)) A[0, 0] = 1 A[0, 1] = 2 B[0, 0] = 1 for i in range(1, m-1): A[i, i-1] = 7 A[i, i] = 8 A[i, i+1] = 9 B[i, 0] = 2 A[m-1, m-2] = 3 A[m-1, m-1] = 4 B[m-1, 0] = 3 print('A \n', A) print('B \n', B) x = np.linalg.solve(A, B)
El programa de solución numérica en el uniforme en cada dirección de la cuadrícula Problema de Dirichlet para la ecuación de convección-difusión
[2]
(9)
Utilizamos aproximaciones por diferencias centrales para el término convectivo y un método iterativo de relajación. Para la dependencia de la tasa de convergencia en el parámetro de relajación para la solución numérica del problema con f (x) = 1 y 6 (x) = 0.10. En la tarea de cuadrícula:
(10)
Representamos la matriz A como la suma de las matrices diagonales, triangulares inferiores y triangulares superiores:
(10)
El método de relajación corresponde al uso del método iterativo :
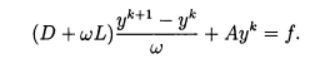
(11)
En
\ hablamos de relajación superior, cuando
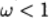
- Sobre la relajación inferior.
Listado de programas from numpy import * """ - . .""" def relaxation(b, f, I1, I2, n1, n2, omega, tol = 1.e-8): h1 = I1 / n1 h2 = I2 / n2 d = 2. / h1**2 + 2. / h2**2 y = zeros([n1+1, n2+1]) ff = zeros([n1+1, n2+1]) bb = zeros([n1+1, n2+1]) for j in arange(1,n2,1): for i in arange(1,n1,1): ff [i,j] = f(i*h1, j*h2) bb[i,j] = b(i*h1, j*h2)
)
Obtenemos:
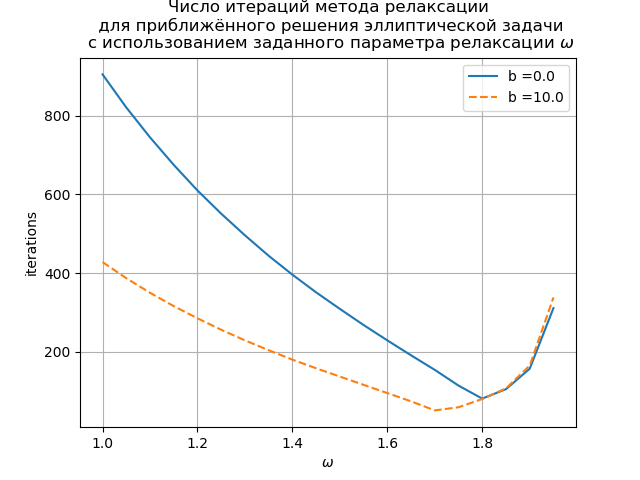
El gráfico muestra la dependencia del número de iteraciones en el parámetro de relajación para la ecuación de Poisson (b (x) = 0) y la ecuación de convección-difusión (b (x) = 10). Para la ecuación de la cuadrícula de Poisson, el valor óptimo del parámetro de relajación se encuentra analíticamente, y el método iterativo converge en
.
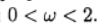
Conclusiones:
- La solución del problema elíptico en Python con un sistema flexible para establecer condiciones de contorno
- Se muestra que el método de relajación tiene un rango óptimo ( 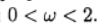) parámetro de relajación.
Referencias
- Ryndin E.A. Métodos para resolver problemas de física matemática. - Taganrog:
Editorial de TRTU, 2003. - 120 p. - Vabishchevich P.N. Métodos numéricos: Taller computacional. - M .: Casa del libro
Librocom, 2010. - 320 p.