Tareas del libro de texto escolar I

Parte 1
Parte II
Parte III

Considere la solución algorítmica al problema número 38 del libro "Tareas para niños de 5 a 15 años"

Calcule la cantidad:

$$

$$\ frac {1} {1 \ cdot2} + \ frac {1} {2 \ cdot3} + \ frac {1} {3 \ cdot4} + ... + \ frac {1} {99 \ cdot100}$$

(con un error de no más del 1% de la respuesta)

A continuación se muestra un algoritmo para calcular sumas parciales de esta serie en Scheme (Lisp) en drRacket (drRacket le permite realizar cálculos en fracciones ordinarias):

#lang racket (define series_sum ( lambda (n) (if (= n 0) 0 (+ (/ 1 (* n (+ n 1))) (series_sum(- n 1))) ) ) ) (series_sum 10) (series_sum 100) (series_sum 1000) (series_sum 10000) (series_sum 100000) (series_sum 1000000) (define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* n (+ n 1.0))) (series_sum_1(- n 1.0))) ) ) ) (series_sum_1 10) (series_sum_1 100) (series_sum_1 1000) (series_sum_1 10000) (series_sum_1 100000) (series_sum_1 1000000) 

Los dos últimos ejemplos drRacket calculados con un error



Este programa se puede ejecutar en línea ide ideone.com y codepad.org .



Si consideramos sumas parciales en fracciones ordinarias, podemos ver que la suma de la serie es

$$

$$\ frac {n} {n + 1}$$

Déjame recordarte que $$$\ lim \ frac {n} {n + 1} = \ frac {1} {1+ \ frac {1} {n}} = \ frac {1} {1} = 1$ a las $$$n \ to \ infty$

El segundo volumen del Curso de cálculo diferencial e integral 363 (4) considera el caso general

$$

$$\ sum \ frac {1} {(\ alpha + n) (\ alpha + n +1)} = \ frac {1} {\ alpha + 1}$$

La tarea del curso "Matemáticas para desarrolladores":
Encuentra el número de miembros en una secuencia $$$\ frac {2n-1} {4n + 5}$ acostado fuera del intervalo $$$(1- \ frac {1} {1000}; 1+ \ frac {1} {1000})$

Pasemos al tema principal del artículo.

Consideremos un ejemplo más de un libro de problemas.
43) Números de conejos (Fibonacci), forman una secuencia $$$(a_ {1} = 1), 1, 3, 5, 8, 13, 21, 34, ...,$ en el cual $$$a_ {n + 2} = a_ {n + 1} + a_ {n}$ para todos $$$n = 1, 2, ...$ . Encuentra el máximo divisor común de números $$$a_ {100}$ y $$$a_ {99}$ .

Respuesta: Dos números adyacentes de Fibonacci son coprimos, es decir. $$$\ gcd (u_ {n + 1}, u_ {n}) = 1$
(mcd es el máximo divisor común, es decir, MCD).

"Prueba del libro" Más allá de las páginas de un libro de texto de matemáticas "[10-11]


En la siguiente tarea, debe calcular la proporción áurea , $$$\ frac {\ sqrt {5} + 1} {2} \ aprox 1.618$ . [Esta es la relación de aspecto de una postal que permanece similar al cortar un cuadrado cuyo lado es el lado más pequeño de la postal]

53) Para una secuencia de números de Fibonacci $$$a_ {n}$ tareas 43 encuentran el límite de la relación $$$\ frac {a_ {n + 1}} {a_ {n}}$ mientras se esfuerza $$$n$ hasta el infinito

$$

$$\ frac {a_ {n + 1}} {a_ {n}} = 2, \ frac {3} {2}, \ frac {5} {3}, \ frac {8} {5}, \ frac { 13} {8}, \ frac {21} {13}, \ frac {34} {21}. $$$

Considere los segmentos que representan las diferencias de dos miembros adyacentes de la serie. $$$\ frac {a_ {n + 1}} {a_ {n}}$ .

Incluso miembros de la serie. $$$\ frac {a_ {n + 1}} {a_ {n}}$ representar una secuencia creciente $$$x_ {n}$

$$

$$\ frac {3} {2}, \ frac {8} {5}, \ frac {21} {13}, ...,$$

Miembros de fila impares $$$\ frac {a_ {n + 1}} {a_ {n}}$ representar una secuencia decreciente $$$y_ {n}$

$$

$$2, \ frac {5} {3}, \ frac {13} {8}, ...,$$

Por el lema de intervalo incrustado (Curso de cálculo diferencial e integral, 38)

$$

$$c = \ lim x_ {n} = \ lim y_ {n}$$

Para nuestra fila en un punto $$$c$ igualdad justa $$$\ frac {a_ {n + 2}} {a_ {n + 1}} = \ frac {a_ {n + 1}} {a_ {n}}$

Dividiendo $$$a_ {n + 2} = a_ {n + 1} + a_ {n}$ en $$$a_ {n + 1}$ obtenemos la ecuación $$$\ frac {a_ {n + 2}} {a_ {n + 1}} = 1 + \ frac {a_ {n}} {a_ {n + 1}}$ .
Al reemplazar $$$\ frac {a_ {n + 2}} {a_ {n + 1}} = x, \ frac {a_ {n}} {a_ {n + 1}} = \ frac {1} {x}$ obtenemos la ecuación cuadrática $$$x = 1 + \ frac {1} {x}$ .

Si en el programa de geogebra conectamos los puntos 2 y $$$\ frac {3} {2}$ , $$$\ frac {3} {2}$ y $$$\ frac {5} {3}$ , $$$\ frac {5} {3}$ y $$$\ frac {8} {5}$ etc. - obtener una figura similar




En general, existe un algoritmo estándar para calcular los números de Fibonacci en Python.
Este algoritmo está disponible en Python.org

 def fib(n): a, b = 0, 1 while a < n: print(a) a, b = b, a+b fib(100) 

Puedes consultar el enlace
Cambie este algoritmo para que imprima una aproximación a la proporción áurea. Para dos números adyacentes a y b, dividiremos la suma a + b por b

 def fib(n): a, b = 0.0 , 1.0 while a < n: print((a+b)/b) a, b = b, a+b fib(100) 

Puedes consultar el enlace

Aquí hay algunas tareas del tutorial SICP con respecto a la proporción áurea.


El siguiente ejemplo del libro de tareas "Tareas para niños de 5 a 15 años"
54) Calcular fracción continua infinita

$$

$$1 + \ frac {1} {2 + \ frac {1} {1+ \ frac {1} {2+ \ frac {1} {1+ \ frac {1} {2 + ...}}}}} $$$

UPD Considera la ecuación

$$

$$\ alpha = 1+ \ frac {1} {2 + \ frac {1} {\ alpha}}$$

Según los teoremas 236 y 235 del libro "Teoría de números":

$$

$$\ alpha = \ frac {P_ {1} \ alpha + P_ {0}} {Q_ {1} \ alpha + Q_ {0}}$$

Componimos una tabla de valores $$$P_ {n}$ y $$$Q_ {n}$ a las $$$n = 0,1:$



para que $$$\ alpha = \ frac {3 \ alpha + 1} {2 \ alpha + 1}, 2 \ alpha ^ {2} - 2 \ alpha -1 = 0$

y desde $$$\ alpha> 0,$ entonces

$$

$$\ alpha = \ frac {1 + \ sqrt {3}} {2}$$

Considere el problema del libro "Detrás de las páginas de un libro de texto de matemáticas" [10-11]
4) Muestra ese número $$$\ sqrt {1+ \ sqrt {1 + \ sqrt {1 + ...}}}$ igual al número $$$\ varphi$ definiendo la proporción áurea.

Considera la opción $$$x_ {n} = \ sqrt {c + \ sqrt {c + ... + \ sqrt {c}}}$
Curso de cálculo diferencial e integral, 35 (2)

De esta manera $$$x_ {n + 1}$ obtenido de $$$x_ {n}$ de acuerdo con la fórmula

$$

$$x_ {n + 1} = \ sqrt {c + x_ {n}}$$

... Por el teorema principal, opciones $$$x_ {n}$ tiene un límite finito $$$a$ . Para determinarlo, pasamos al límite en la igualdad

$$

$$x_ {n + 1} ^ {2} = c + x_ {n}; $$$

Nos metemos de tal manera que $$$a$ satisface la ecuación cuadrática

$$

$$a ^ {2} = c + a$$

Esta ecuación tiene las raíces de diferentes signos; pero el límite que nos interesa $$$a$ no puede ser negativo, por lo tanto, es exactamente igual a la raíz positiva:

$$

$$a = \ frac {\ sqrt {4c + 1} + 1} {2}$$

De lo cual podemos concluir que la "proporción áurea" es una solución a la ecuación $$$a ^ {2} = c + a$
a las $$$c = 1$ .


Además, en el Curso de cálculo diferencial e integral, 35 (3), se considera un algoritmo para calcular el número inverso

Dejar $$$c$ Es cualquier número positivo, y pon $$$x_ {n} = cy_ {n}$ . La relación de recurrencia escrita arriba será reemplazada por:

$$

$$y_ {n + 1} = y_ {n} (2 - cy_ {n})$$

Tomando el valor inicial $$$y_ {0}$ bajo la condición: $$$0 <y_ {0} <\ frac {1} {c}$ lo entendemos $$$y_ {n}$ aumentando monótonamente, tenderá a $$$\ frac {1} {c}$ . Según este esquema, en las máquinas de conteo, se calcula el número inverso $$$c$ .

Algoritmo de cálculo de números inversos $$$c$ en Python:
( Ideone.com y codepad.org )

 def reciprocal(c,y0,n): arr=[] for i in range(n): arr.append(y0) y0=y0*(2-c*y0) return arr 

La función recíproca toma un número como entrada $$$c$ valor inicial $$$y_ {0}$ , número de iteraciones $$$n$ y devuelve una serie de "aproximaciones" al número $$$\ frac {1} {c}$ .
$$$y_ {0} = 0.1$ a las $$$c <10$
$$$y_ {0} = 0.01$ a las $$$10 <c <100$
$$$y_ {0} = 0.001$ a las $$$100 <c <1000$
etc.
Ejemplos de cómo funciona la función recíproca con varios $$$c$

 >>> reciprocal(3,0.1,10) 

[0.1, 0.17, 0.2533, 0.31411733000000003, 0.3322255689810133, 0.3333296519077525,
0.3333333332926746, 0.3333333333333333337, 0.3333333333333333337, 0.33333333333333337]

 >>> reciprocal(8,0.1,10) 

[0.1, 0.12, 0.1248, 0.12499968, 0.1249999999991808, 0.125, 0.125, 0.125, 0.125, 0.125]

 >>> reciprocal(5,0.1,10) 

[0.1, 0.15000000000000002, 0.18750000000000003, 0.19921875000000003, 0.19999694824218753, 0.1999999999534339, 0.20000000000000004, 0.19999999999999998,
0.19999999999999998, 0.19999999999999998]

Interpretación geométrica

Intentemos usar el método tangente para aproximar el número inverso.
Tangentes $$$y = f '(x_ {0}) (x-x_ {0}) + f (x_ {0})$ para funcionar gráfico $$$y = \ frac {1} {x}$ son expresados ​​por la fórmula $$$y = \ frac {2} {x_ {0}} - \ frac {x} {x_ {0} ^ {2}}$

Números de sustitución $$$1,2,3,4, ...$ en lugar de $$$x_ {0}$ obtenemos las ecuaciones de las tangentes

$$

$$y = 2-x$$

$$

$$y = 1- \ frac {x} {4}$$

$$

$$y = \ frac {2} {3} - \ frac {x} {9}$$

$$

$$y = \ frac {1} {2} - \ frac {x} {16}$$

Construye estos gráficos


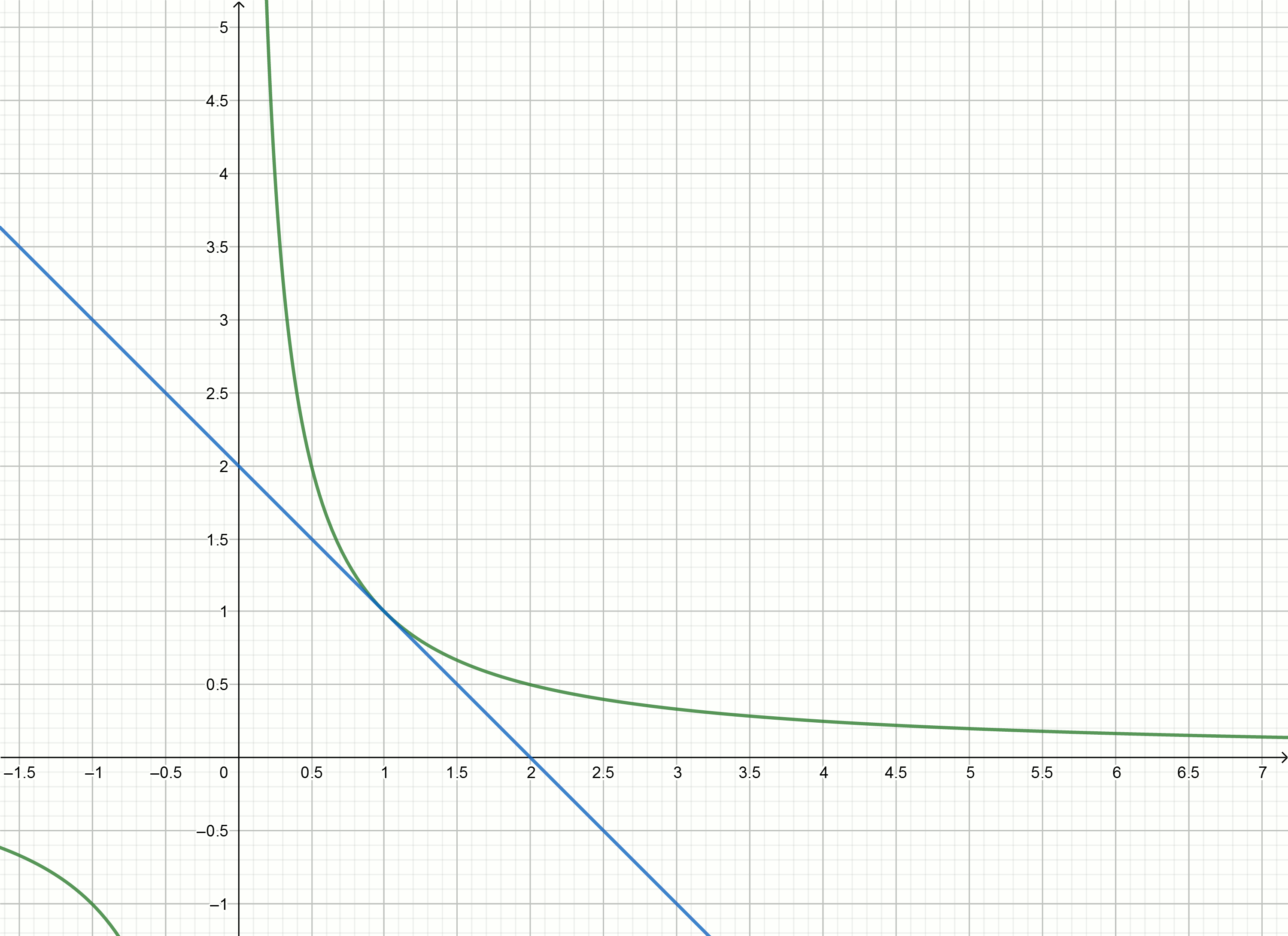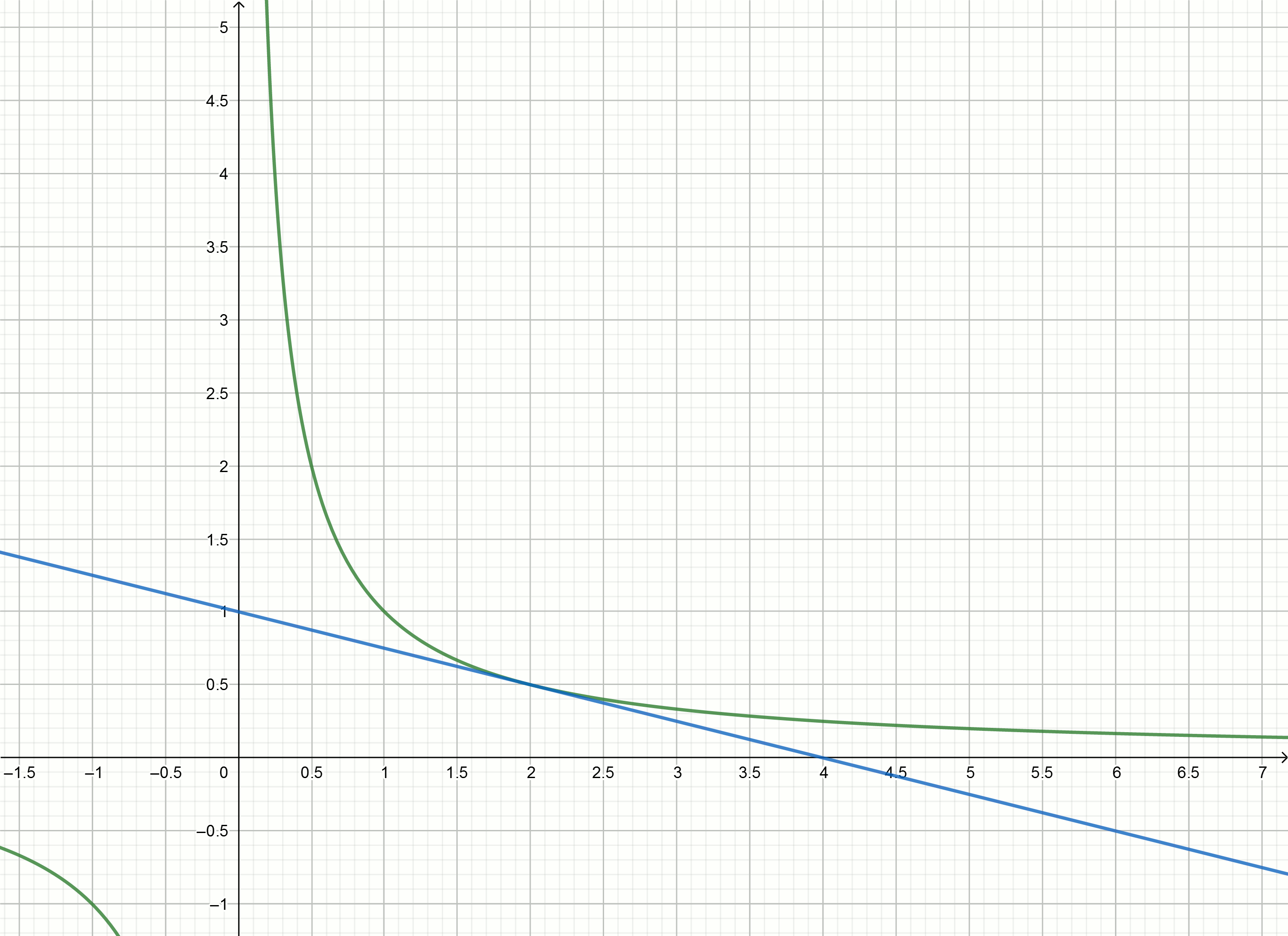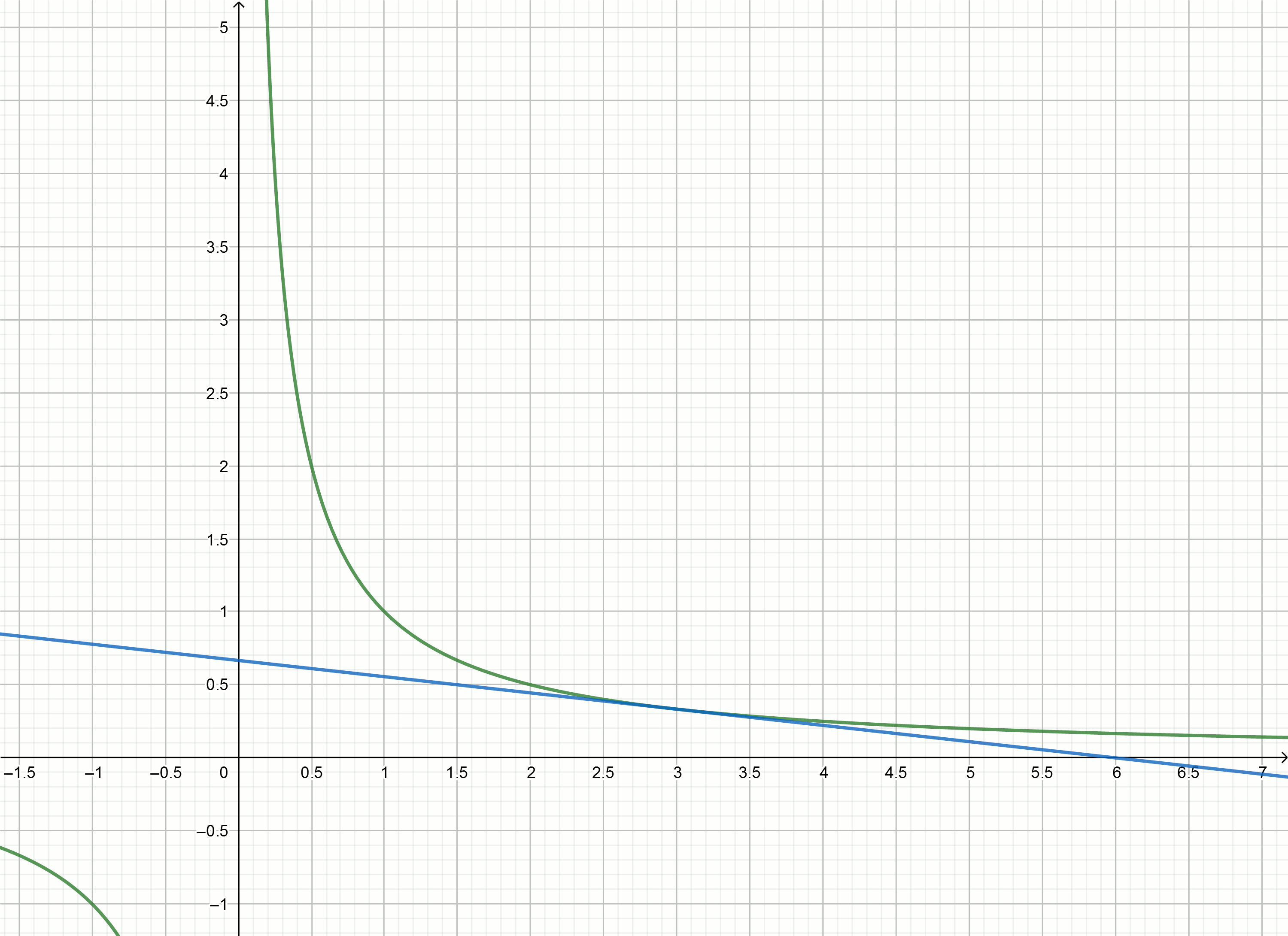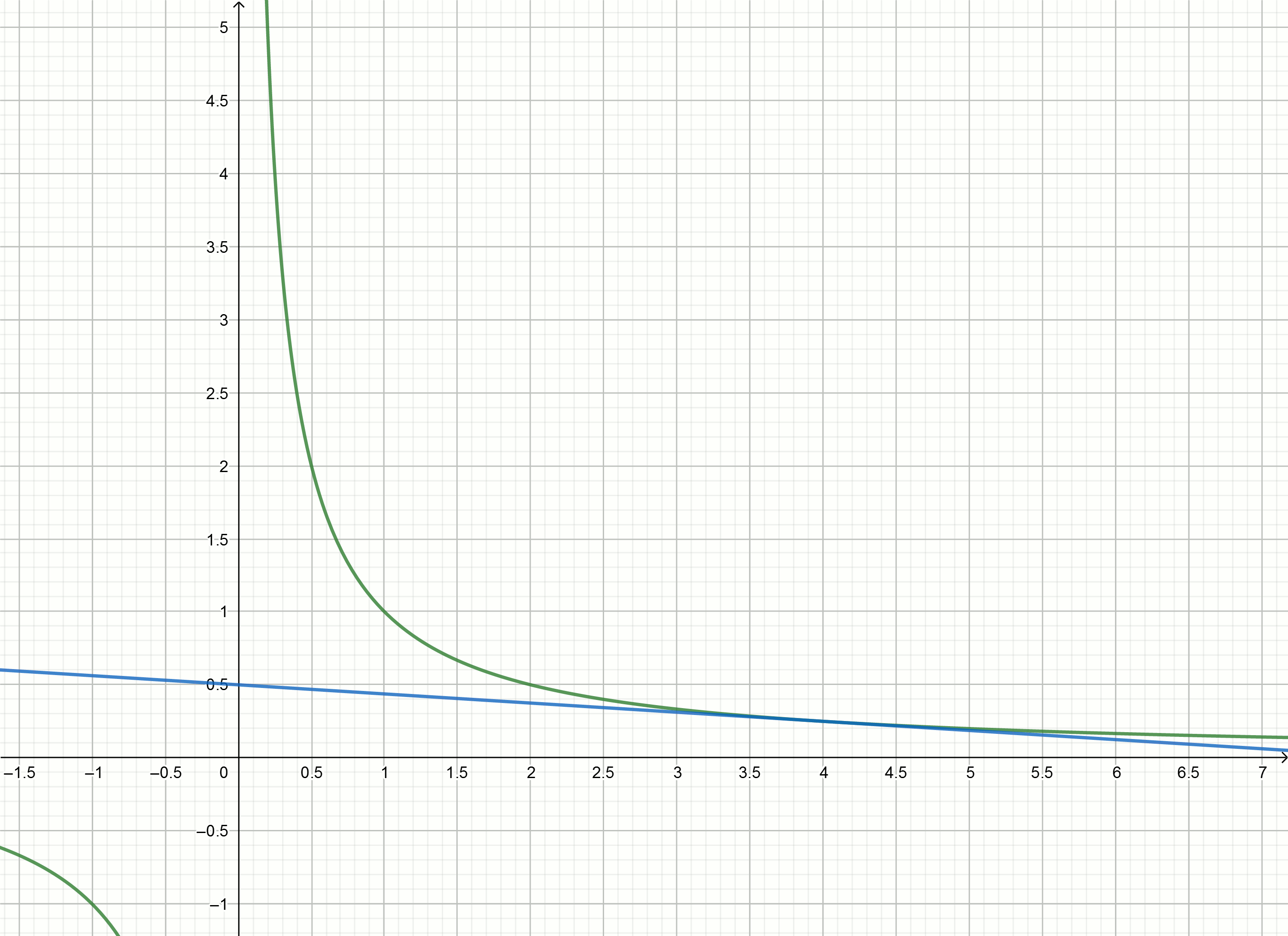
Si mueve la hipérbola hacia abajo $$$\ alpha$ , luego cruza el eje de abscisas en el punto $$$\ frac {1} {\ alpha}$ .
La ecuación tangente se convierte en $$$y = \ frac {2} {x_ {0}} - \ frac {x} {x_ {0} ^ {2}} - \ alpha$
Además, equiparar la ecuación de la tangente a cero y expresar $$$x$ obtenemos la ecuación $$$x = x_ {0} - \ frac {f (x_ {0})} {f '(x_ {0})}$

En cambio $$$f (x_ {0})$ sustituto $$$\ frac {1} {x_ {0}} - \ alpha$
En cambio $$$f '(x_ {0})$ sustituto $$$- \ frac {1} {x_ {0} ^ {2}}$

Obtenemos la expresión $$$x = x_ {0} + (\ frac {1} {x_ {0}} - \ alpha) x_ {0} ^ {2}$
Expandiendo los corchetes, obtenemos $$$x = x_ {0} + x_ {0} - \ alpha x_ {0} ^ {2}$

Sustituto $$$0.1$ en la ecuación $$$x = x_ {0} (2- \ alpha x_ {0})$ y ver qué valores "correrán" $$$x$ a las $$$\ alpha = 2$ tenemos $$$0.1, 0.18, 0.29, 0.42, 0.49, 0.5$

Sustituyendo estos valores en la ecuación $$$y = \ frac {2} {x_ {0}} - \ frac {x} {x_ {0} ^ {2}} - 2$ nos ponemos directos

$$

$$y = 0.111 - \ frac {x} {0.897}$$

$$

$$y = 0.222 - \ frac {x} {0.81}$$

$$

$$y = 0.816 - \ frac {x} {0.504}$$

$$

$$y = 0.857 - \ frac {x} {0.49}$$

$$

$$y = 1.5 - \ frac {x} {0.326}$$

$$

$$y = 2 - \ frac {x} {0.25}$$

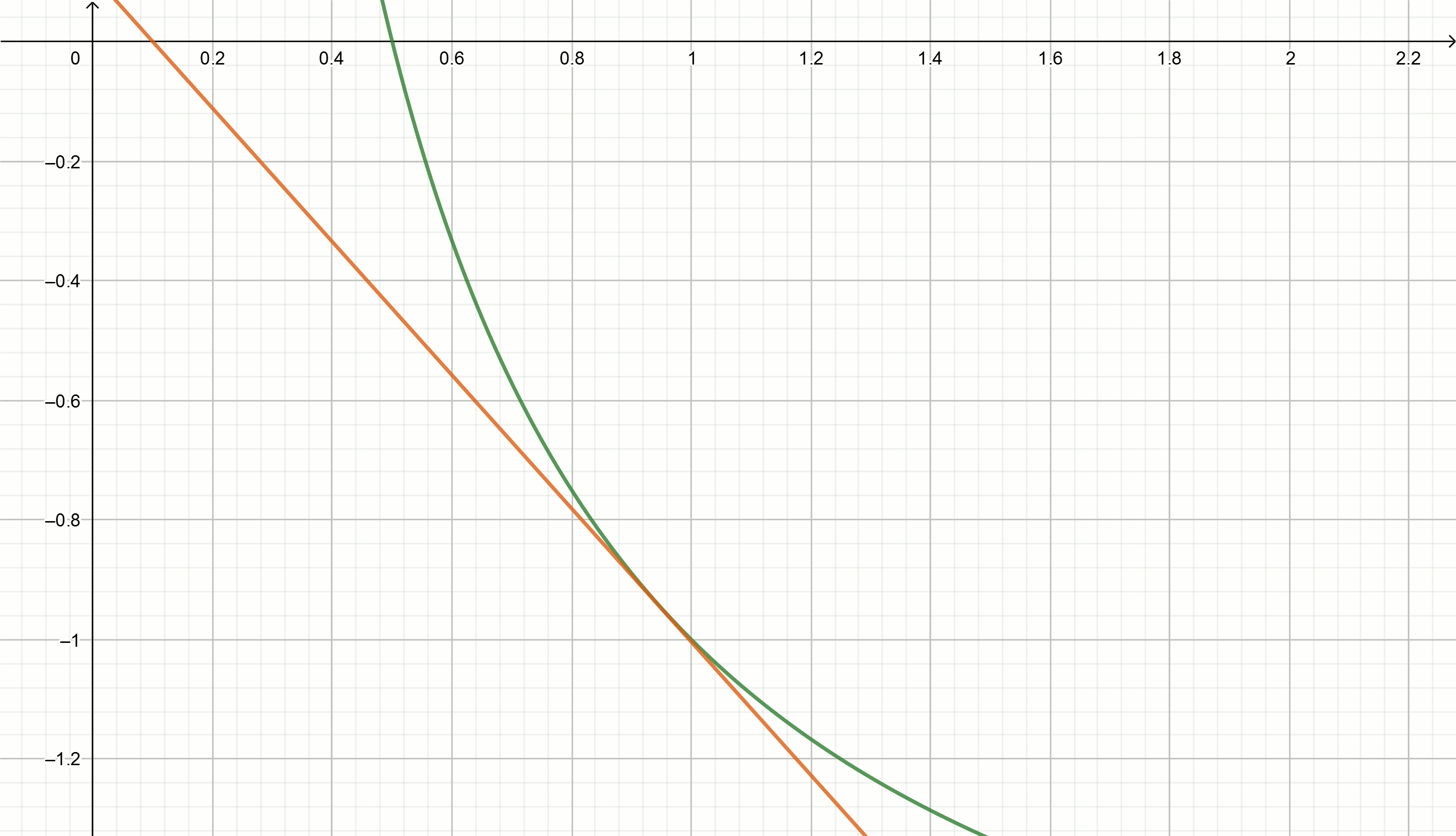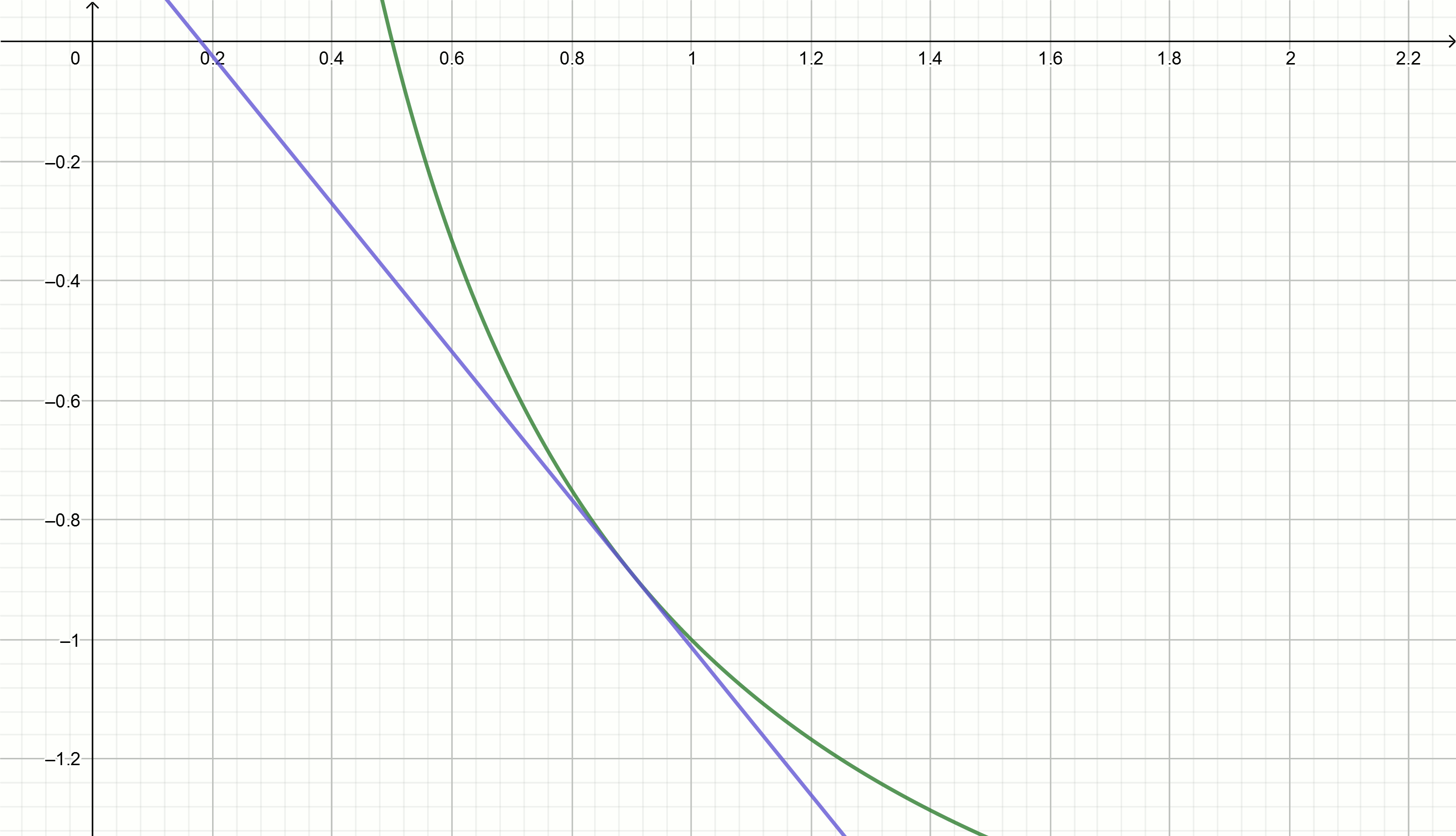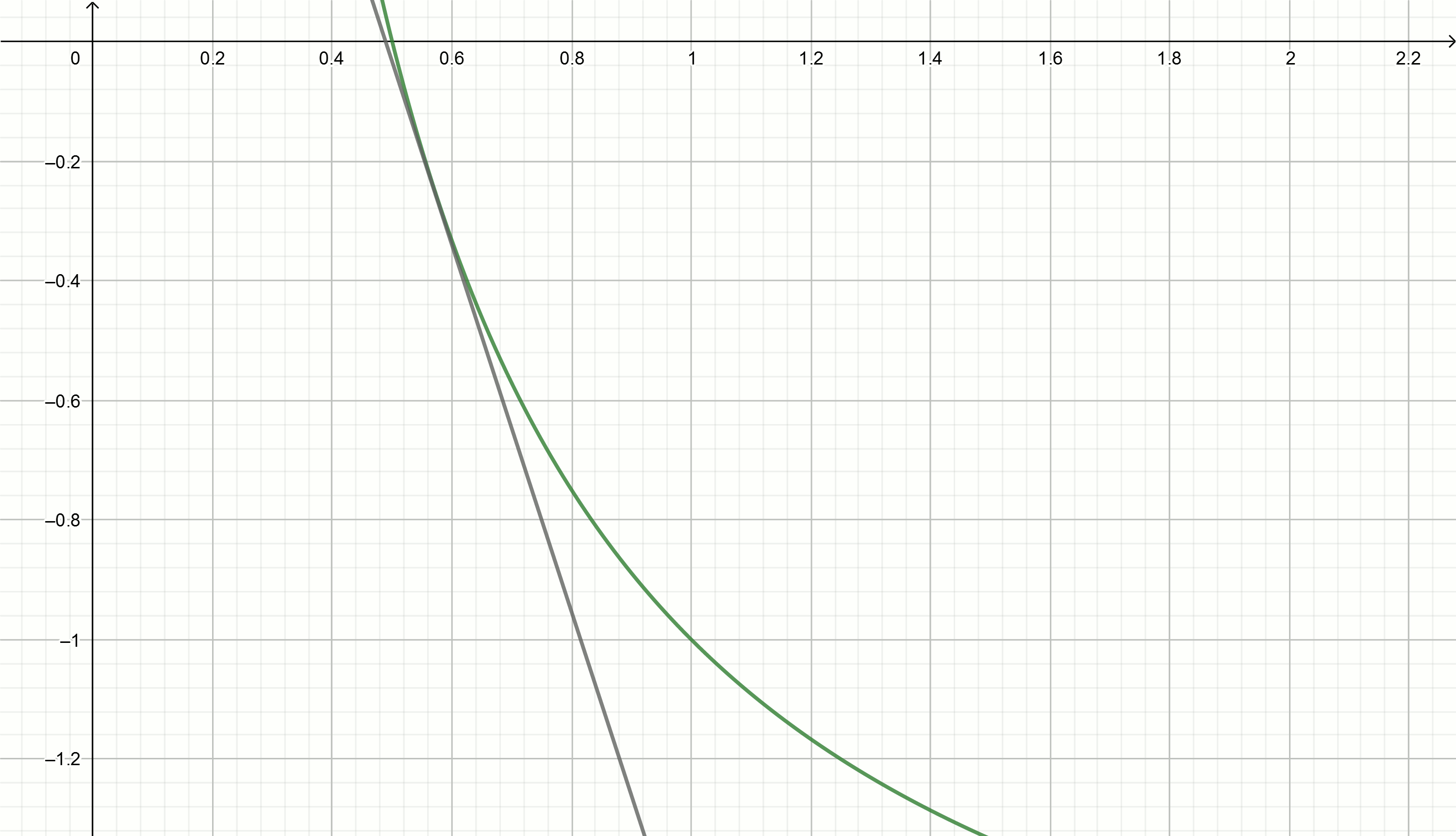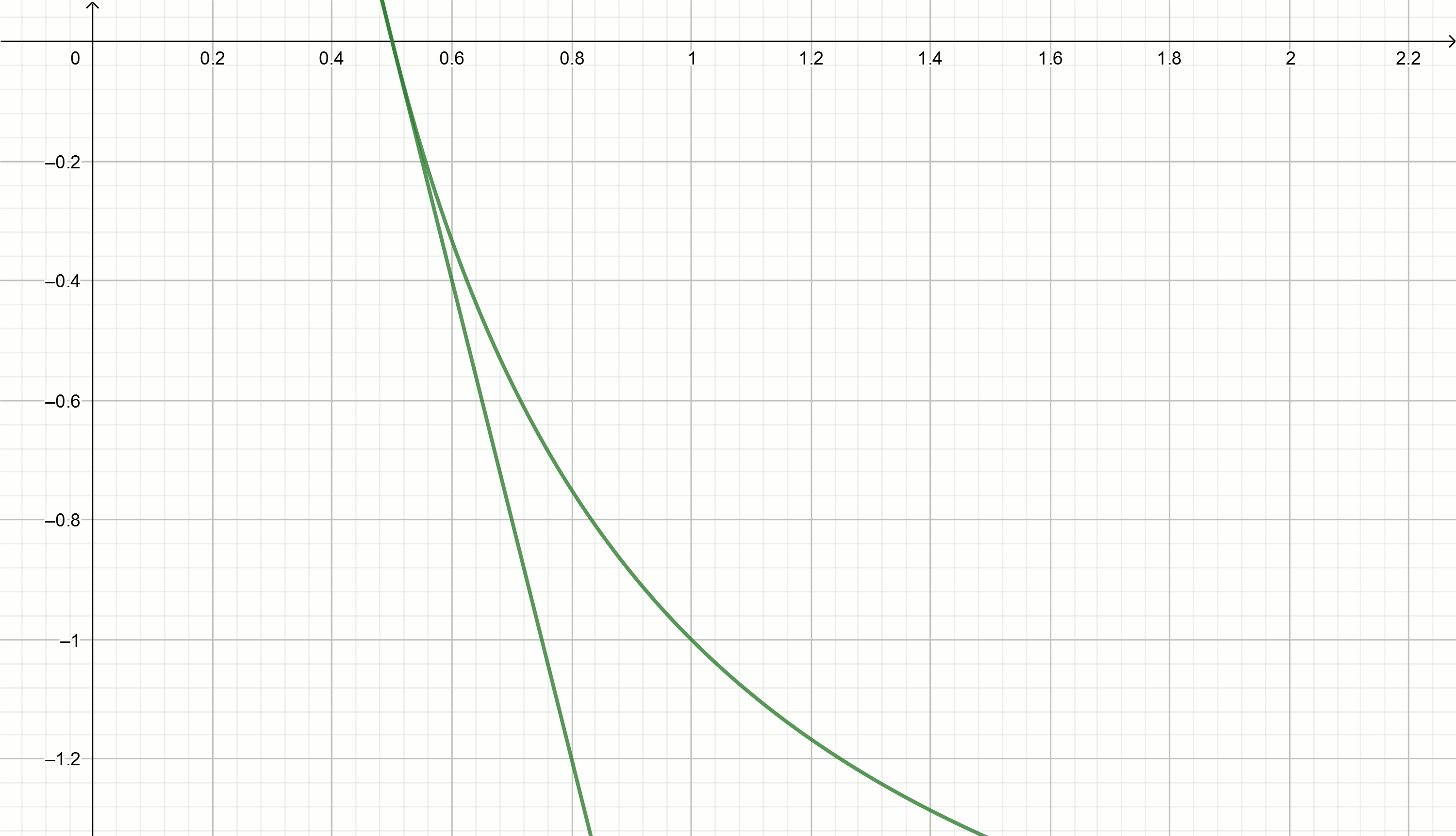
Extracción de raíz cuadrada

Volviendo a las expresiones irracionales, consideramos un método iterativo para extraer la raíz cuadrada.
Escribiremos un algoritmo usando el método iterativo Heron

$$

$$x_ {n + 1} = \ frac {1} {2} (x_ {n} + \ frac {a} {x_ {n}})$$

 def square_root(a,n): # a -  , n -   x0=1 #    1 arr=[] for i in range(n): arr.append(x0) #      x0=0.5*(x0+a/x0) #      return arr print square_root(2,10) 

codepad.org

Cálculo de la raíz cuadrada utilizando fracciones continuas utilizadas por Rafael Bombelli

Para encontrar el valor $$$\ sqrt {n}$ , primero definimos toda su aproximación: $$$\ sqrt {n} = a \ pm r$ donde $$$0 <r <1$ . Entonces $$$n = (a \ pm r) ^ {2} = a ^ {2} \ pm 2ar + r ^ {2}$ . A partir de aquí es fácil deducir que $$$r = {\ frac {| n-a ^ {2} |} {2a \ pm r}}$ . Reemplazar la expresión resultante en la fórmula $$$\ sqrt {n} = a \ pm r$ , obtenemos una expansión de fracción continua:

$$

$$a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm \ cdots}}}}}}$$

Entonces, podemos escribir el algoritmo de extracción de raíz cuadrada usando descomposición en una fracción continua

 def square_root(n,a,n_count): # n- , a -    x0=a #    a arr=[] for i in range(n_count): #       a arr.append(x0-a) #  a x0=2*a+(na*a)/x0 return arr print square_root(2.0,1.0,10) 

codepad.org

En general, los números reales y complejos, así como las funciones de una o más variables, pueden ser numeradores y denominadores privados.
El método de extracción de la parte entera le permite a uno representar un número irracional en forma de una fracción continua infinita con unidades en los numeradores (numeradores frecuentes iguales a la unidad).
Aquí hay un ejemplo de una expansión fraccional continua de un número $$$\ sqrt {5}$ del libro "Álgebra"

$$

$$\ sqrt {5} -2 = \ frac {(\ sqrt {5} -2) (\ sqrt {5} +2)} {\ sqrt {5} +2} = \ frac {1} {\ sqrt { 5} +2}$$

De esta manera $$$\ sqrt {5} = 2+ \ frac {1} {\ sqrt {5} +2}$

Seleccione la parte entera del número. $$$\ sqrt {5} +2: E (\ sqrt {5} +2) = 4$ . Significa $$$\ sqrt {5} +2$ puede ser representado como $$$4 + \ alpha$ . Está claro que $$$\ alpha = \ sqrt {5} + 2-4 = \ sqrt {5} -2$ por lo tanto $$$\ sqrt {5} + 2 = 4 + \ sqrt {5} + 2$ . Nuevamente, destruimos la irracionalidad en el numerador del segundo término:

$$

$$\ sqrt {5} -2 = \ frac {1} {\ sqrt {5} +2}$$

El resultado es:

$$

$$\ sqrt {5} = 2 + \ frac {1} {4+ \ frac {1} {\ sqrt {5} +2}}$$

Hagamos otro paso similar:

$$

$$\ sqrt {5} = 2 + \ frac {1} {4+ \ frac {1} {4+ \ frac {1} {\ sqrt {5} +2}}}$$

Es fácil ver que el proceso de aislar toda la parte y la formación de una fracción continua en este ejemplo no tiene fin. En cada nuevo denominador aparecerá $$$4$ y plazo $$$\ sqrt {5} -2$ . Por lo tanto, está claro que $$$\ sqrt {5}$ se representa como una fracción continua infinita:

$$

$$\ sqrt {5} = [2, 4, 4, 4, ...]$$

Hipótesis

Si $$$d \ in \ mathbb {N}, \ sqrt {d} \ notin \ mathbb {N}$ entonces la fracción continua del número $$$\ sqrt {d} + [\ sqrt {d}]$ puramente periódico
Evarist Galois demostró esta hipótesis.

Es decir si a la parte no periódica de la fracción $$$[1; 2,2,2, ...] = \ sqrt {2}$ agrega toda la parte $$$[\ sqrt {2}] = 1$ entonces obtenemos una fracción puramente periódica $$$[2,2,2, ...]$ .

$$$\ sqrt {3} = [1; 1,2, ...];$
$$$\ sqrt {3} +1 = [2,1, ...]$

$$$\ sqrt {5} = [2; 4,4,4, ...];$
$$$\ sqrt {5} +2 = [4,4,4, ...]$

$$$\ sqrt {6} = [2; 2,4, ...]; $$
$$$\ sqrt {6} +2 = [4,2, ...]$

$$$\ sqrt {13} = [3; 1,1,1,1,6, ...];$
$$$\ sqrt {13} +3 = [6,1,1,1,1,1, ...]$


Si en la descomposición de la raíz según el método de Bombelli

$$

$$\ sqrt {n} = a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ { 2} |} {2a \ pm \ cdots}}}}}}}$$

agregar al primer término $$$a$ , obtenemos una fracción puramente periódica

$$

$$\ sqrt {n} + a = 2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm {\ frac {| na ^ {2} |} {2a \ pm \ cdots}}}}}}}$$

Queda por llevar la fracción a una forma más familiar (con unidades en el numerador).
Divide el numerador y el denominador de la fracción entre $$$| n-a ^ {2} | $$ obtenemos la expresión

$$

$$\ sqrt {n} + a = 2 a \ pm {\ frac {1} {\ frac {2a} {| na ^ {2} |} \ pm {\ frac {1} {2a \ pm {\ frac { 1} {\ frac {2a} {| na ^ {2} |} \ pm \ cdots}}}}}}}$$

De esta manera

$$

$$\ sqrt {2} +1 = 2+ \ frac {1} {\ frac {2} {1} + \ frac {1} {2 + \ frac {1} {\ frac {2} {1} +. ..}}} = [2,2,2, ...]$$

$$

$$\ sqrt {3} +1 = 2+ \ frac {1} {\ frac {2} {2} + \ frac {1} {2 + \ frac {1} {\ frac {2} {2} +. ..}}} = [2,1, ...]$$

$$

$$\ sqrt {5} +2 = 4+ \ frac {1} {\ frac {4} {1} + \ frac {1} {4 + \ frac {1} {\ frac {4} {1} +. ..}}} = [4,4,4, ...]$$

$$

$$\ sqrt {6} +2 = 4+ \ frac {1} {\ frac {4} {2} + \ frac {1} {4 + \ frac {1} {\ frac {4} {2} +. ..}}} = [4,2, ...]$$

$$

$$\ sqrt {13} +3 = 6+ \ frac {1} {\ frac {6} {4} + \ frac {1} {6 + \ frac {1} {\ frac {6} {4} +. ..}}} = [6, \ frac {3} {2}, ...]$$

Escribiremos un programa que calcule la aproximación de fracción continua $$$[6, \ frac {3} {2}, ...]$

 #lang racket (define continued_fraction ( lambda (n) (if (= n 0) 1 (+ 6 (/ 1 (+ 3/2 (/ 1 (continued_fraction(- n 1)))))) ))) (continued_fraction 4) 

codepad.org
En el cuarto paso obtenemos $$$6 \ frac {3818} {6305}$ que es igual $$$6.60555114 ...$ mientras que $$$\ sqrt {13} +3 \ aprox. 6.60555127$ .




PS Resuelva el problema ("Problemas para niños de 5 a 15 años")
27) Probar que el resto de la división de un número $$$2 ^ {p-1}$ impar impar
$$$p$ es igual a $$$1$
(ejemplos: $$$2 ^ {2} = 3a + 1, 2 ^ {4} = 5b + 1, 2 ^ {6} = 7c + 1, 2 ^ {10} -1 = 1023 = 10 \ cdot 93)$ .
Este problema se considera en el artículo Amazing Adventures of Continued Fractions de la revista Quantum.

Libros:
"Tareas para niños de 5 a 15 años" V. I. Arnold.
"El curso del cálculo diferencial e integral" G. M. Fichtenholtz
"Teoría de los números" A. A. Buchstab
"Detrás de las páginas de un libro de texto de matemáticas" N. Ya. Vilenkin, L. P. Shibasov, Z. F. Shibasova
"Álgebra" N. Ya. Vilenkin, R. S. Guter, S. I. Schwarzburd
Aritmética digital Ercegovac Milos D., Lang Tomas
"La estructura e interpretación de los programas de computadora" Harold Abelson, Gerald Sassman

Ver también
El artículo "Sobre una tarea que ya no se ofrece en la entrevista".
El blog de Spice IT Recruitment publica tareas de entrevistas en varias empresas.
Tareas para entrevistas en Yandex.
En este video, A. Savvateev resuelve problemas con entrevistas en Tesla.