Métodos numéricos para resolver sistemas de ecuaciones no lineales.

Introduccion

Muchos problemas aplicados conducen a la necesidad de encontrar una solución general a un sistema de ecuaciones no lineales. No se encontró una solución analítica general del sistema de ecuaciones no lineales. Solo hay métodos numéricos.

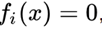
Cabe señalar un hecho interesante de que cualquier sistema de ecuaciones sobre números reales puede representarse mediante una ecuación equivalente, si tomamos todas las ecuaciones en la forma , cuadrarlos y doblarlos.

Para la solución numérica, se utilizan métodos iterativos de aproximaciones sucesivas (iteración simple) y el método de Newton en varias modificaciones. Los procesos iterativos se generalizan naturalmente al caso de un sistema de ecuaciones no lineales de la forma:

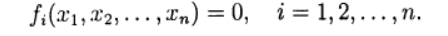
(1)

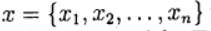
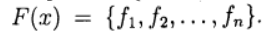
Denote por vector de incógnitas y definir una función vectorial Entonces el sistema (1) se escribe en la forma de la ecuación:

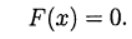
(2)

Ahora, volvamos a nuestro amado Python y notemos su primacía entre los lenguajes de programación que quieren aprender [1].



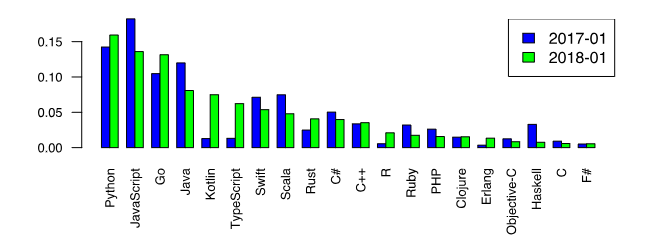
Este hecho es un incentivo adicional para considerar métodos numéricos en Python. Sin embargo, existe una opinión entre los amantes de Python de que las funciones especiales de la biblioteca, como scipy.optimize.root, spsolve_trianular, newton_krylov , son la mejor opción para resolver problemas por métodos numéricos.

Es difícil estar en desacuerdo con esto, aunque solo sea porque la variedad de módulos también ha llevado a Python a la cima de la popularidad. Sin embargo, hay casos en los que, incluso con un examen superficial, el uso de métodos conocidos directos sin usar funciones especiales de la biblioteca SciPy también da buenos resultados. En otras palabras, lo nuevo es lo viejo y olvidado.

Entonces, en la publicación [2], sobre la base de experimentos computacionales, se demostró que la función de biblioteca newton_krylov, diseñada para resolver grandes sistemas de ecuaciones no lineales, tiene la mitad de velocidad que el algoritmo TSLS + WD
(mínimos cuadrados de dos pasos) implementado por la biblioteca NumPy.

El propósito de esta publicación es comparar el número de iteraciones, la velocidad y, lo más importante, el resultado de resolver un problema modelo en forma de un sistema de cien ecuaciones algebraicas no lineales usando la función de biblioteca scipy.optimize.root y el método Newton implementado usando la biblioteca NumPy.

Capacidades de resolución Scipy.optimize.root para resolver numéricamente sistemas de ecuaciones no lineales algebraicas

La función de biblioteca scipy.optimize.root se eligió como base de comparación porque tiene una extensa biblioteca de métodos adecuados para el análisis comparativo.

scipy.optimize.root ( diversión, x0, args = (), método = 'hybr', jac = Ninguno, tol = Ninguno, devolución de llamada = Ninguno, ptions = Ninguno )
fun - Una función vectorial para encontrar la raíz.
x0 - Condiciones iniciales para encontrar raíces

método:
hybr: se utiliza la modificación Powell del método híbrido;
lm - resuelve sistemas de ecuaciones no lineales usando el método de mínimos cuadrados.
Como se deduce de la documentación [3], los métodos broyden1, broyden2, anderson, linearmixing, diagbroyden, emocionantemixing, krylov son los métodos exactos de Newton. Los parámetros restantes son "opcionales" y se pueden encontrar en la documentación.

Métodos para resolver sistemas de ecuaciones no lineales.

El material que figura a continuación puede leerse en la literatura, por ejemplo, en [4], pero respeto a mi lector y, para su comodidad, si es posible, presento la derivación del método de forma resumida. Aquellos a quienes no les gustan las fórmulas se saltan esta sección.

En el método de Newton, una nueva aproximación para resolver el sistema de ecuaciones (2) se determina a partir de la solución del sistema de ecuaciones lineales :

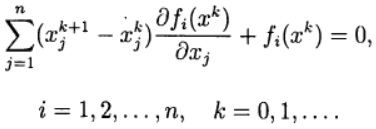
(3)

Defina la matriz de Jacobi:

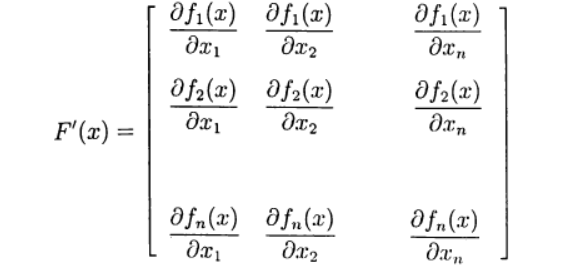
(4)

Escribimos (3) en la forma:

(5)

Muchos métodos de un solo paso para la solución aproximada de (2) por analogía con métodos iterativos de dos capas para resolver sistemas de ecuaciones algebraicas lineales se pueden escribir en la forma:

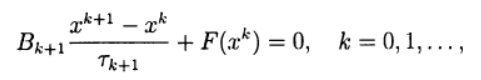
(6)

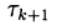
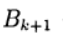
donde Son parámetros iterativos, un - una matriz cuadrada n x n que tiene el inverso.

Cuando se usa el registro (6), el método de Newton (5) corresponde a la elección:



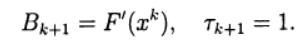
El sistema de ecuaciones lineales (5) para encontrar una nueva aproximación se puede resolver de forma iterativa. En este caso, tenemos un proceso iterativo de dos etapas con iteraciones externas e internas. Por ejemplo, un proceso iterativo externo puede llevarse a cabo de acuerdo con el método de Newton, y las iteraciones internas pueden llevarse a cabo sobre la base del método iterativo de Seidel.

Al resolver sistemas de ecuaciones no lineales, uno puede usar análogos directos de métodos iterativos estándar que se usan para resolver sistemas de ecuaciones lineales. El método no lineal de Seidel aplicado a la solución (2) da:

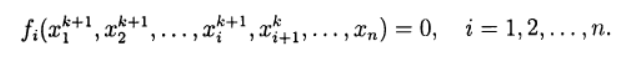
(7)

En este caso, cada componente de la nueva aproximación a partir de la solución de la ecuación no lineal se puede obtener sobre la base del método de iteración simple y el método de Newton en varias modificaciones. Por lo tanto, nuevamente llegamos a un método iterativo de dos etapas en el que las iteraciones externas se llevan a cabo de acuerdo con el método de Seidel, y las iteraciones internas se realizan utilizando el método de Newton.

Las principales dificultades computacionales en la aplicación del método de Newton para la solución aproximada de sistemas de ecuaciones no lineales están relacionadas con la necesidad de resolver un sistema lineal de ecuaciones con una matriz de Jacobi en cada iteración , y esta matriz cambia de iteración a iteración. En el método Newton modificado, la matriz de Jacobi se invierte solo una vez:

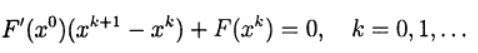
(8)

Selección de funciones del modelo

Tal elección no es una tarea simple, ya que con un aumento en el número de ecuaciones en el sistema de acuerdo con un aumento en el número de variables, el resultado de la solución no debería cambiar, ya que de lo contrario es imposible rastrear la corrección de la solución del sistema de ecuaciones al comparar dos métodos. Traigo la siguiente solución para la función del modelo:

n=100 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i] - x[i-1] - 2*x[i+1] - 2 f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f 

La función f crea un sistema de n ecuaciones no lineales, cuya solución no depende del número de ecuaciones y es igual a la unidad para cada una de las n variables.

Un programa para probar una función modelo con los resultados de resolver un sistema de ecuaciones no lineales algebraicas usando la función de biblioteca optimice.root para diferentes métodos de encontrar raíces

 from numpy import* from scipy import optimize import time ti = time.clock() n=100 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i] - x[i-1] - 2*x[i+1] - 2 f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f x0 =zeros([n]) sol = optimize.root(f,x0, method='krylov') print('Solution:\n', sol.x) print('Krylov method iteration = ',sol.nit) print('Optimize root time', round(time.clock()-ti,3), 'seconds') 

Solo uno de los métodos dados en la documentación [3] pasó las pruebas en el resultado de resolver una función modelo, este es el método 'krylov' .

Solución para n = 100:

Solución:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Iteración del método de Krylov = 4219
Optimizar el tiempo de raíz 7.239 segundos:


Conclusión: con un aumento en el número de ecuaciones en un factor de dos, la aparición de errores en la solución es notable. Con un aumento adicional en n, la solución se vuelve inaceptable, lo que es posible debido a la adaptación automática al paso, la misma razón para una fuerte caída en el rendimiento. Pero esto es solo mi suposición.

Un programa para probar una función modelo con los resultados de resolver un sistema de ecuaciones no lineales algebraicas usando un programa escrito en Python 3 teniendo en cuenta las relaciones (1) - (8) para encontrar las raíces usando el método Newton modificado

Solución para n = 100:

Solución:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Iteración de Newton = 13
Tiempo del método de Newton 0.496 segundos

Solución para n = 200:

Solución:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1.]
Iteración de Newton = 14
Newton método tiempo 1.869 segundos

Para asegurarnos de que el programa realmente resuelva el sistema, reescribimos la función del modelo para evitar la raíz con un valor de 1 en la forma:

 n=10 def f(x): f = zeros([n]) for i in arange(0,n-1,1): f[i] = (3 + 2*x[i])*x[i]*sin([i]) - x[i-1] - 2*x[i+1] - 2+e**-x[i] f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3 f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4 return f 

Obtenemos:
Solución:
[0.96472166 0.87777036 0.48175823 -0.26190496 -0.63693762 0.49232062
-1.31649896 0.6865098 0.89609091 0.98509235]
Iteración de Newton = 16
Tiempo del método de Newton 0.046 segundos

Conclusión: el programa también funciona cuando cambia la función del modelo.

Ahora volvemos a la función del modelo inicial y verificamos un rango más amplio para n, por ejemplo, en 2 y 500.
n = 2
Solución:
[1. 1.]
Iteración de Newton = 6
Newton método tiempo 0.048 segundos
n = 500

Conclusiones:

Un programa escrito en Python usando el método Newton modificado, cuando resuelve sistemas de ecuaciones no lineales de la función de modelo dada, tiene más estabilidad de solución que cuando resuelve usando la función de biblioteca optimice.root (f, x0, método = 'krylov') para el método Krylov. En cuanto a la velocidad de la conclusión final, es imposible dibujar debido al enfoque diferente para el control de pasos.

Referencias

1. Valoración de lenguajes de programación 2018.
2. Cooper I.V., Faleychik B.V. Procesos iterativos no matriciales con supresión de error cuadrático medio raíz para grandes sistemas de ecuaciones no lineales.
3. scipy.optimize.root.
4. Vabishchevich P.N. Métodos numéricos: taller computacional. - M .: Casa del libro "LIBROCOM", 2010. - 320 p.