Construyendo órbitas de cuerpos celestes usando Python

Sistemas de referencia para determinar la órbita.

Para encontrar las trayectorias de los movimientos relativos en la mecánica clásica, se utiliza la suposición del tiempo absoluto en todos los marcos de referencia (tanto inerciales como no inerciales).

Usando esta suposición, consideramos el movimiento del mismo punto en dos marcos de referencia diferentes $$$K$ y $$$K ^ {'}$ de los cuales el segundo se mueve con relación al primero a una velocidad arbitraria $$$\ vec {V (t)} = \ dot {\ vec {R (t)}}$ donde $$$\ vec {R (t)}$ vector de radio que describe la posición del origen del sistema de coordenadas $$$K ^ {'}$ relativo al marco de referencia $$$K$ )

Describiremos el movimiento de un punto en el sistema. $$$K ^ {'}$ vector de radio $$$\ vec {r ^ {'}} (t)$ dirigido desde el origen del sistema $$$K ^ {'}$ a la posición actual del punto. Luego, el movimiento del punto considerado en relación con el marco de referencia $$$K$ descrito por un vector de radio $$$\ vec {r (t)}$ :

$$$\ vec {r} (t) = \ vec {r ^ {'}} (t) + \ vec {R} (t)$ , (1)

y velocidad relativa $$$\ vec {v (t)}$

$$$\ vec {v} (t) = \ dot {\ vec {r ^ {'}}} (t) + \ dot {\ vec {R}} (t)$ , (2)

donde $$$\ dot {\ vec {r ^ {'}}} (t)$ - velocidad del punto relativo al sistema $$$K ^ {'}$ ; $$$\ dot {\ vec {R}} (t)$ velocidad de cuadro $$$K ^ {'}$ relativo al marco de referencia $$$K$ .



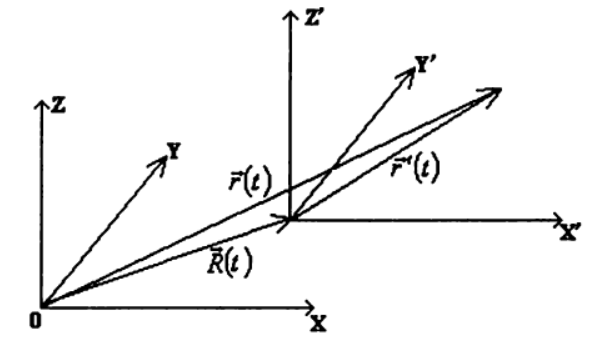
Por lo tanto, para encontrar la ley de movimiento de un punto en un marco de referencia arbitrario $$$K$ necesario:

1) establecer la ley de movimiento del punto - $$$\ vec {r ^ {'}} (t)$ relativo al marco de referencia $$$K ^ {'}$ ;
2) establecer la ley de movimiento - $$$\ vec {R} (t)$ sistemas de referencia $$$K ^ {'}$ relativo al marco de referencia $$$K$
3) determinar la ley de movimiento del punto - $$$\ vec {r} (t) = \ vec {r ^ {'}} (t) + \ vec {R} (t)$ relativo al marco de referencia $$$K$ .

Construcción de la órbita de la luna en el marco de referencia heliocéntrico.

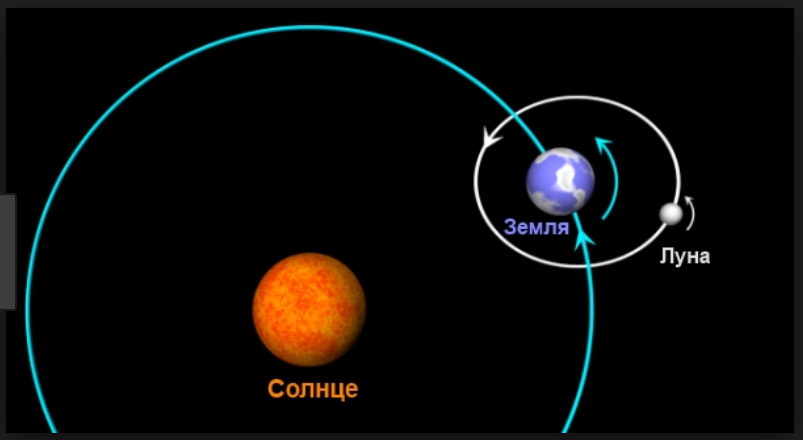
En el sistema de referencia heliocéntrico (sistema $$$K$ ) La Tierra se mueve en un círculo de radio
$$$R_ {1} = 1.496 \ cdot 10 ^ {8}$ km (período de circulación $$$T_ {1} = 3,156 \ cdot 10 ^ {7}$ s.). La luna, a su vez, se mueve alrededor de la Tierra (sistema K ') alrededor de un círculo de radio. $$$R_ {2} = 3.844 \ cdot 10 ^ {5}$ km (período de circulación $$$T_ {2} = 2.36 \ cdot 10 ^ {6}$ s Como se sabe [1,2], cuando un punto material se mueve a lo largo de un círculo de radio $$$R$ con velocidad angular constante $$$\ omega$ Las coordenadas del vector de radio dibujado desde el origen hasta la posición actual del punto cambian de acuerdo con la ley:

$$

$$\ vec {R (t)} = \ binom {R \ cdot cos (\ omega \ cdot t + \ varphi _ {0})} {R \ cdot sin (\ omega \ cdot t + \ varphi _ {0})} = \ binom {R \ cdot cos (\ frac {2 \ pi} {T}) + \ varphi _ {0})} {R \ cdot sin (\ frac {2 \ pi} {T} + \ varphi _ { 0})}, (3)$$

donde $$$\ varphi _ {0}$ - la fase inicial que caracteriza la posición de la partícula en el tiempo $$$t = 0$ , que en el futuro asumiremos que es igual a cero. Sustitución en (3) $$$R$ en $$$R_ {1}$ y $$$R_ {2}$ y sustituyendo en (1), obtenemos la dependencia del vector de radio de la luna en el sistema de coordenadas heliocéntricas en el tiempo:

$$

$$\ vec {r (t)} = \ binom {x (t)} {y (t)} = \ binom {R_ {2} cos (\ frac {2 \ pi} {T_ {2}} t) + R_ {1} cos (\ frac {2 \ pi} {T_ {1}} t)} {R_ {2} sin (\ frac {2 \ pi} {T_ {2}} t) + R_ {1} sin (\ frac {2 \ pi} {T_ {1}} t)}, (4)$$

La expresión (4) establece la órbita de la Luna ( $$$y = y (x (t))$ ) en forma paramétrica, donde el parámetro es el tiempo. Para construir la órbita deseada usando Python, establecemos los radios de las órbitas y los períodos de rotación de la Tierra y la Luna.

La Tierra se mueve en un sistema de coordenadas heliocéntricas ( $$$K$ ) su radio orbital y el período de revolución son respectivamente iguales $$$R_ {1} = 1.496 \ cdot 10 ^ {8} km, T_ {1} = 3.156 \ cdot 10 ^ {7} s$ La luna se mueve alrededor de la tierra en un sistema de coordenadas ( $$$K ^ {'}$ ) su radio orbital y el período de revolución son respectivamente iguales $$$R_ {2} = 3.844 \ cdot 10 ^ {5} km, T_ {2} = 2.36 \ cdot 10 ^ {6} s$ .

En vista de (4), determinamos las funciones de la dependencia de las coordenadas en el tiempo:

$$

$$\ binom {(X (t) = R_ {1} \ cdot cos (\ frac {2 \ pi} {T_ {1}} \ cdot t), Y (t) = R_ {1} \ cdot sin (\ frac {2 \ pi} {T_ {1}} \ cdot t)} {x (t) = R_ {2} \ cdot cos (\ frac {2 \ pi} {T_ {2}} \ cdot t), y (t) = R_ {2} \ cdot sin (\ frac {2 \ pi} {T_ {2}} \ cdot t)}, (5)$$

Usando (5), obtenemos un par de coordenadas para la órbita de la luna:

$$

$$\ binom {X_ {g} (t) = X (t) + x (t)} {Y_ {g} (t) = Y (t) + y (t)}, (6)$$

Establecemos el número de puntos en los que se calculan las coordenadas N = 1000 y el tiempo discreto en el intervalo del período de rotación de la Tierra. $$$dt = \ frac {T_ {1}} {N}$ . Escribiremos un programa y crearemos un gráfico para el área de cambio de coordenadas positivas:


Obtenemos:


Fig. 1

El horario creado le permite expandir la tarea de entrenamiento y ver cuál será la órbita de la luna si el radio de la órbita de la luna es $$$R_ {2} = 3.844 \ cdot 10 ^ {7}$ . . Está claro para el lector que ni siquiera tiene un conocimiento especial en astronomía que la Luna no puede tener esa órbita en campos no gravitacionales de la Tierra, y se utiliza un radio hipotético para estudiar las condiciones para la aparición de bucles . Haremos los cambios apropiados al programa:


Obtenemos:


Fig.2

Al comparar las órbitas de la luna que se muestran en la Fig. 1 y 2, encontramos sus diferencias significativas. Para explicar las razones de estas diferencias, es necesario comparar las velocidades lineales de la luna en el primer y segundo caso y la velocidad lineal de la tierra.

Dado que la dirección de la velocidad lineal de la Tierra en relación con el Sol, así como la dirección de la velocidad lineal de la Luna en relación con la Tierra, cambia en el tiempo y la velocidad permanece constante en magnitud.

Como una característica cuantitativa de la relación de las velocidades lineales de la luna y la tierra en un sistema de coordenadas heliocéntricas, uno debe elegir la diferencia entre el módulo de velocidad lineal de la tierra y la proyección de la velocidad lineal de la luna en la dirección de la velocidad lineal de la tierra:

$$

$$v_ {o} (t) = \ left | \ vec {V} (t) \ right | - \ frac {(\ vec {V} (t) \ cdot \ vec {v} (t))} {\ left | \ vec {V} (t) \ right |}, (7)$$

Definimos las funciones que describen las leyes de cambio de los componentes de la velocidad de la Tierra y la Luna:

$$

$$\ begin {matrix} V_ {x} (t) = \ frac {d} {dt} X (t), V_ {y} (t) = \ frac {d} {dt} Y (t) & \\ vx (t) = \ frac {d} {dt} x (t), vy (t) = \ frac {d} {dt} y (t) \ end {matrix}, (8)$$

Para determinar la velocidad resultante, teniendo en cuenta la proyección, usamos la relación:

$$$D (t) = \ sqrt {V_ {x} (t) ^ {2} + V_ {y} (t) ^ {2}} - \ sqrt {vx (t) ^ {2} + vy (t) ^ {2}} \ cdot \ frac {V_ {x} (t) \ cdot vx (t) + V_ {y} (t) \ cdot vy (t)} {\ sqrt {V_ {x} (t) ^ {2} + V_ {y} (t) ^ {2}} \ cdot \ sqrt {vx (t) ^ {2} + vy (t) ^ {2}}}, (9)$

Escribiremos un programa teniendo en cuenta (5), (8), (9) y el radio de la órbita de la luna $$$R_ {2} = 3.844 \ cdot 10 ^ {5}$ km.:


Obtenemos:


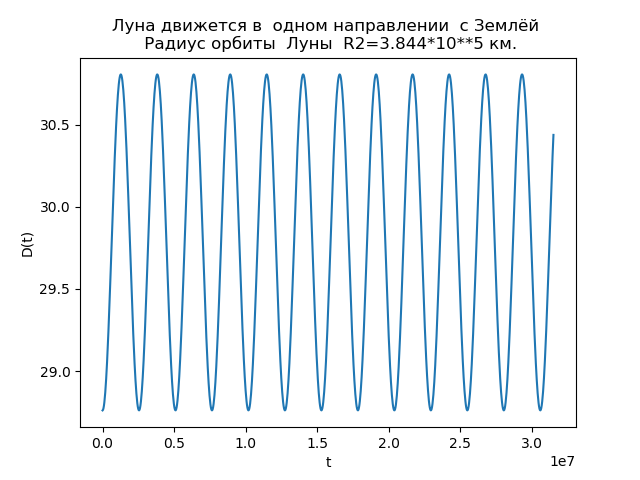Fig.3.

Escribiremos un programa teniendo en cuenta (5), (8), (9) y el radio de la órbita de la Luna R2 = 3.844 * 10 ** 7 km:


Obtenemos:


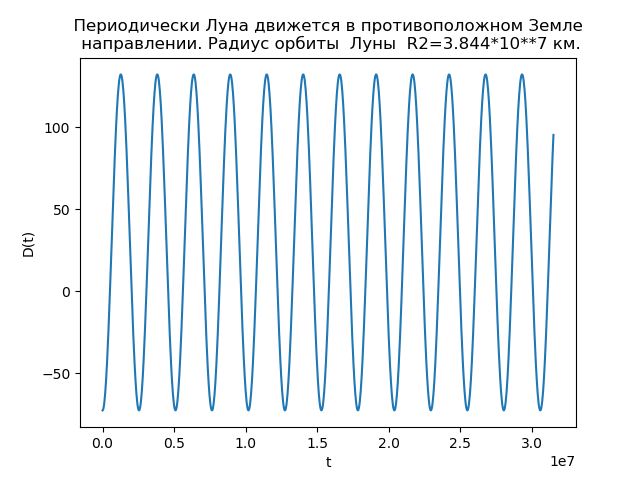Fig.4.

El análisis de las dependencias nos permite explicar la razón de las diferencias en las órbitas. La función D (t) para $$$R_ {2} = 3.844 \ cdot 10 ^ {5}$ km siempre es positivo, es decir, la luna siempre se mueve en la dirección del movimiento de la Tierra y no se forman bucles. En $$$R_ {2} = 3.844 \ cdot 10 ^ {7}$ valor de km $$$D (t)$ toma valores negativos, y hay momentos en que la luna se mueve en la dirección opuesta a la dirección del movimiento de la tierra, y por lo tanto la órbita tiene bucles. Este era el significado de usar la órbita inexistente de la luna en los cálculos.

Construcción de la órbita de Marte en el marco de referencia asociado con la Tierra.

.


En el sistema de referencia heliocéntrico (sistema K), la Tierra se mueve en un círculo de radio $$$R_ {1} = 1.496 \ cdot 10 ^ {8}$ km, periodo de circulación $$$T_ {1} = $ 365.2$ día, Marte se mueve a lo largo de una elipse, cuyo eje semi mayor $$$am = 2.28 \ cdot 10 ^ {8}$ km, el período de revolución de Marte $$$T_ {m} = $ 689,9$ días., la excentricidad de la órbita $$$e = $ 0.09$ [3] El movimiento de la Tierra se describe mediante el vector de radio R (t) definido por la expresión (3). Debido al hecho de que la órbita de Marte es una elipse, dependencias $$$x = x (t), y = y (t)$ desde el tiempo se configuran paramétricamente [4]:

$$$x (\ varepsilon) = a_ {m} \ cdot (cos (\ varepsilon) -e)$ , (10)

$$$y (\ varepsilon) = a_ {m} \ cdot \ sqrt {1-e ^ {2}} \ cdot sin (\ varepsilon)$ , (11)

$$$t (\ varepsilon) = \ frac {T_ {m}} {2 \ pi} \ cdot (\ varepsilon-e \ cdot sin (\ varepsilon))$ , (12)

Una revolución de elipse completa corresponde a un cambio en el parámetro <img $$$\ varepsilon$ de 0 a $$$2 \ pi$ . Para construir la órbita de Marte, es necesario calcular las coordenadas de los vectores de radio en los mismos momentos que describen la posición de la Tierra y Marte en el marco de referencia heliocéntrico, luego de acuerdo con la relación $$$\ vec {r ^ {'}} (t) = \ vec {r} (t) - \ vec {R} (t)$ Calcule las coordenadas de Marte en el marco de referencia asociado con la Tierra.

Para construir la órbita de Marte en el marco de referencia conectado con la Tierra, utilizamos los parámetros dados previamente de las órbitas de la Tierra y Marte, las relaciones (10) - (12), y también las relaciones para las coordenadas de la Tierra:

$$$X (t) = R_ {1} \ cdot cos (\ frac {2 \ pi} {T_ {1}} t)$ , (13)

$$$Y (t) = R_ {1} \ cdot sin (\ frac {2 \ pi} {T_ {1}} t)$ , (14)

Cabe señalar que el número de períodos de revolución de Marte alrededor del Sol es $$$K = 9$ , entonces el número de puntos en los que se debe hacer el cálculo y la distancia entre ellos se determinará a partir de las relaciones:

$$$N = 4000 \ cdot K, \ varepsilon_ {i} = \ frac {2 \ pi} {N} \ cdot i, i = 0 ... N$ (15)


Obtenemos:


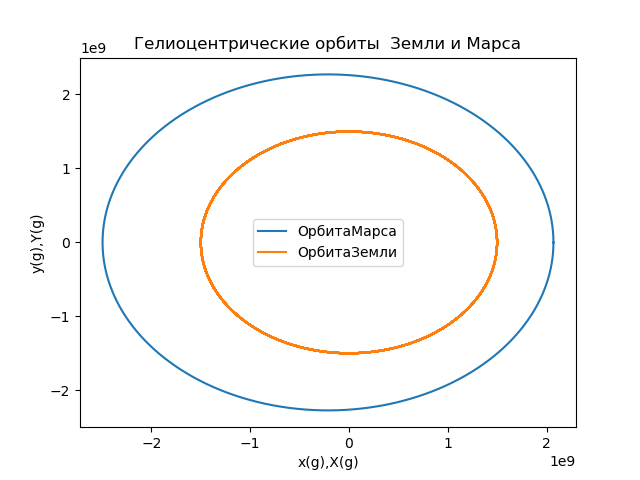Fig.5

Calculamos las coordenadas del vector de radio que describe la posición de Marte en el marco de referencia conectado con la Tierra, y construimos las órbitas (Fig. 6) usando la relación:

$$$x1_ {i} = x (\ varepsilon_ {i}) - X (t (\ varepsilon_ {i})), y1_ {i} = y (\ varepsilon_ {i}) - Y (t (\ varepsilon_ {i} ))$ (16)


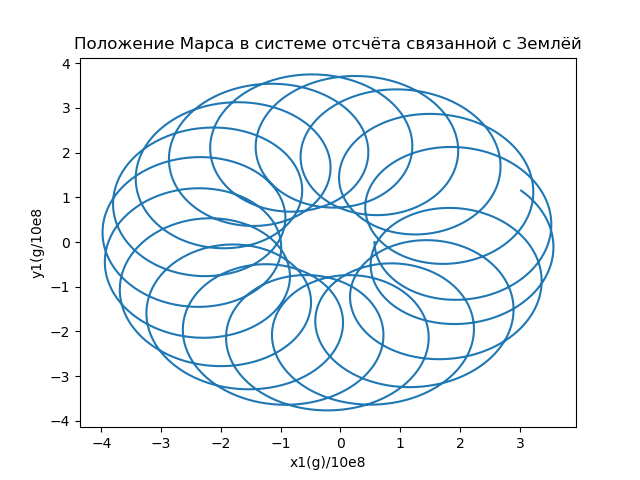Fig.6

Otra característica importante del movimiento de Marte (principalmente para vuelos espaciales interplanetarios) es la distancia entre la Tierra y Marte s (t), que está determinada por el módulo del vector de radio que describe la posición de Marte en el marco de referencia asociado con la Tierra. La figura 7 presenta la dependencia de la distancia entre la Tierra y Marte en el tiempo medido en años terrestres.


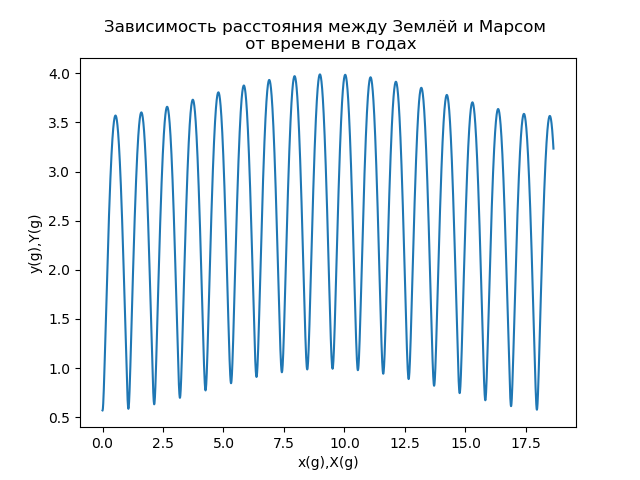Fig. 7

Un análisis de la dependencia que se muestra en la Fig. 7 muestra que la distancia entre la Tierra y Marte es una función periódica compleja del tiempo. Si usamos la terminología de la teoría de la señal [5], entonces podemos decir acerca de la dependencia s (t) de que es una señal de amplitud modulada, que generalmente se representa como el producto de dos funciones de una función de alta frecuencia (portadora) y de baja frecuencia que define la modulación de amplitud (envolvente) :

$$$u (t) = (\ bar {u} + a \ cdot sin (\ omega_ {1} t)) \ cdot (1+ \ Delta a \ cdot sin (\ omega_ {2} t))$ (17)

donde $$$\ bar {u}$ - componente constante de la función $$$u (t)$ ; $$$a$ - amplitud de señal; $$$\ omega_ {1}$ - frecuencia portadora; $$$\ Delta a$ - la amplitud de la función que establece la profundidad de la modulación de amplitud; $$$\ omega_ {2}$ - frecuencia de la función de modulación.

De la Fig. 7 se puede ver que el período del portador es de aproximadamente 2 años, el período de la función de modulación es de aproximadamente 17 años [6].

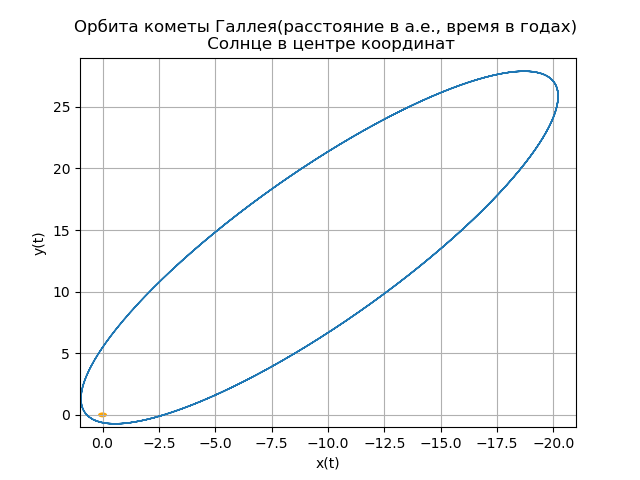
Construcción de la órbita heliocéntrica del cometa Halley

La última vez que el cometa Halley pasó a través de su perihelio (el punto de órbita más cercano al Sol) el 9 de febrero de 1986. (Se considera que el Sol mismo está ubicado en el origen).

Las coordenadas y componentes de velocidad del cometa Halley en ese momento eran iguales $$$p_ {0} = (0.325514, 0.459460, 0.166229)$ y $$$v_ {0} = (–9.096111, –6.916686, –1.305721)$ respectivamente, y la distancia aquí se expresa en unidades astronómicas de longitud - a.u.d., o simplemente a.u. (unidad astronómica, es decir, la longitud de los principales semiaxis principales de la órbita de la Tierra), y el tiempo en años. En estas unidades de medida, las ecuaciones tridimensionales de movimiento del cometa tienen la forma:

$$

$$\ left \ {\ begin {matrix} \ frac {d ^ {2} x} {dt ^ {2}} = - \ frac {\ mu \ cdot x} {r ^ {3}} \\ \ frac { d ^ {2} y} {dt ^ {2}} = - \ frac {\ mu \ cdot y} {r ^ {3}} \\ \ frac {d ^ {2} z} {dt ^ {2} } = - \ frac {\ mu \ cdot z} {r ^ {3}} \ end {matrix} \ right., (18)$$

(18)

donde: $$$\ mu = 4 \ pi ^ {2}, r = \ sqrt {x ^ {2} + y ^ {2} + z ^ {2}}$


Obtenemos:









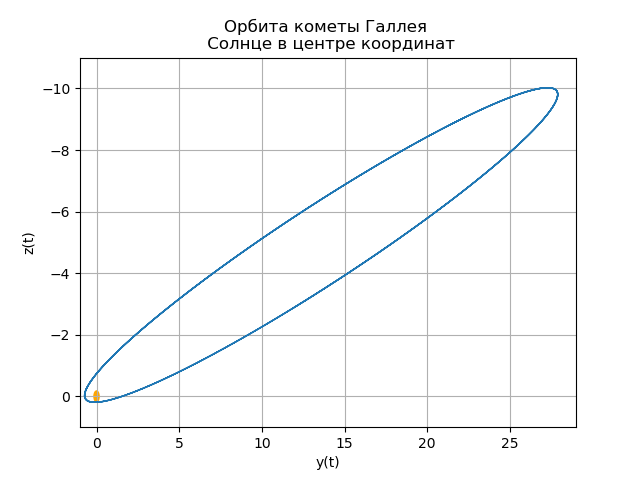
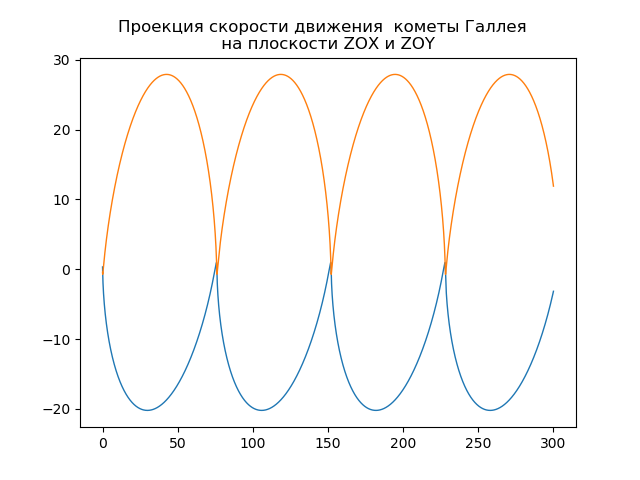Tu propio cometa

Prueba un experimento. Por la noche, montas tu telescopio en la cima de una colina no muy lejos de tu casa. La noche debe ser clara, sin nubes, estrellada y, si la fortuna te sonríe: a las 0.30 a.m. notarás un nuevo cometa.

Después de repetidas observaciones en las siguientes noches, podrá calcular sus coordenadas en esa primera noche. Coordenadas en el sistema de coordenadas heliocéntricas: P0 = (x0, y0, z0) y el vector de velocidad v0 = (vx0, vy0, vz0).

Usando estos datos, determine:

• la distancia del cometa al Sol en el perihelio (el punto de órbita más cercano al Sol) y en el afelio (el punto de órbita más alejado del Sol);
• velocidad del cometa cuando pasa a través del perihelio y a través del afelio;
• el período de revolución del cometa alrededor del Sol;
• En las dos fechas siguientes, el cometa pasa a través del perihelio.

Si medimos la distancia en unidades astronómicas y el tiempo en años, entonces la ecuación de movimiento del cometa tomará la forma (18). Para su propio cometa, seleccione coordenadas iniciales arbitrarias y velocidades del mismo orden que el cometa Halley.

Si es necesario, vuelva a hacer una elección arbitraria de la posición inicial y el vector de velocidad hasta obtener una órbita excéntrica plausible que vaya más allá de la órbita de la Tierra (como la mayoría de los cometas reales).

Referencias

1. Feynman R., Leighton R., Sands M. Feynman Lectures in Physics. 3ra ed. T. 1.-2. M .: Mir, 1977.
2. Matveev A.N. Mecánica y teoría de la relatividad. M .: Superior. escuela., 1986.
3. Enciclopedia Física T. 3. M .: Big Russian Encyclopedia, 1992.
4. Landau L.D., Lifshits E.M. Curso de Física Teórica. La mecanica. M .: Fu-matgiz, 1958.
5. Baskakov S.I. Circuitos y señales de ingeniería de radio. M .: Superior. escuela., 1988.
6. Porshnev C.V. Simulación por computadora de procesos físicos utilizando el paquete mathcad .