Cómo en 1C: Enterprise resolvemos sistemas de ecuaciones algebraicas

Trabajar con matrices numéricas en general y resolver sistemas de ecuaciones algebraicas lineales en particular es un problema matemático y algorítmico clásico que se usa ampliamente en el modelado y el cálculo de una gran clase de procesos comerciales (por ejemplo, al calcular el costo). Al crear y operar configuraciones 1C: Enterprise, muchos desarrolladores se enfrentaron a la necesidad de implementar manualmente algoritmos de cálculo SLAU, y luego con el problema de una larga espera para una solución.

"1C: Enterprise" 8.3.14 contendrá una funcionalidad que puede reducir significativamente el tiempo que lleva resolver sistemas de ecuaciones lineales utilizando un algoritmo basado en la teoría de grafos.

Está optimizado para su uso en datos que tienen una estructura dispersa (es decir, que no contiene más del 10% de coeficientes distintos de cero en las ecuaciones) y, en promedio y en el mejor de los casos, muestra los asintóticos (n⋅log (n) ⋅log (n)), donde n es el número de variables y, en el peor de los casos (cuando el sistema está lleno ~ 100%), su comportamiento asintótico es comparable con los algoritmos clásicos (Θ (n ³ )). Además, en sistemas con ~ 10 ⁵ incógnitas, el algoritmo muestra la aceleración cientos de veces en comparación con los implementados en bibliotecas de álgebra lineal especializadas (por ejemplo, superlu o lapack ).


Importante: el artículo y el algoritmo descrito requieren una comprensión de álgebra lineal y teoría de grafos en el nivel de primer año de una universidad.

Presentación del SLAE como gráfico.

Considere el sistema disperso más simple de ecuaciones lineales:


Atención: el sistema se genera aleatoriamente y se usará más tarde para demostrar los pasos del algoritmo

A primera vista, surge una asociación con otro objeto matemático: la matriz de adyacencia del gráfico. Entonces, ¿por qué no convertir los datos a listas de adyacencia, ahorrar RAM en tiempo de ejecución y acelerar el acceso a coeficientes distintos de cero?

Para hacer esto, es suficiente transponer la matriz y establecer la invariante “A [i] [j] = z ⇔ la variable i-ésima ingresa la ecuación j-ésima con el coeficiente z” , y luego para cualquier A [i] [j] distinto de cero construya el borde correspondiente del vértice i al vértice j.

El gráfico resultante se verá así:



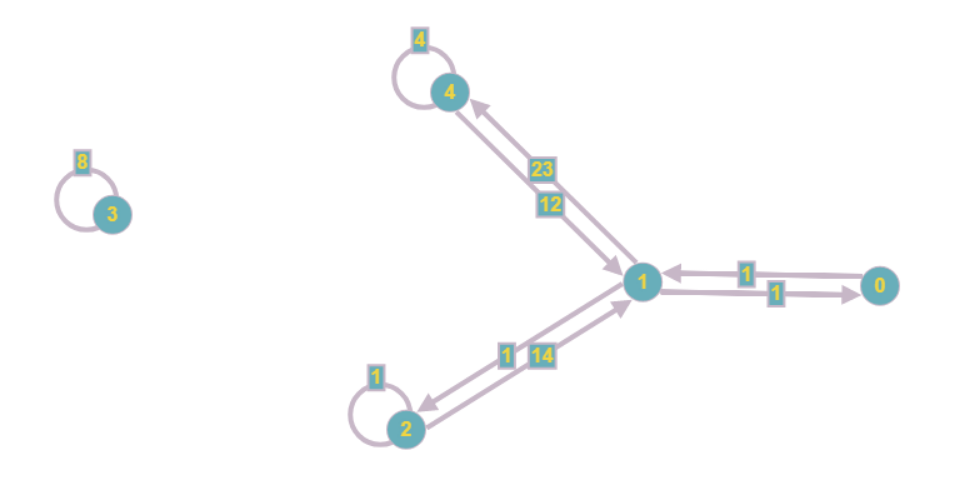
Incluso visualmente, resulta menos engorroso, y los costos de la memoria asintótica disminuyen de O (n ² ) a O (n + m), donde m es el número de coeficientes en el sistema.

Aislamiento de componentes débilmente conectados.

La segunda idea algorítmica que viene a la mente al considerar la entidad resultante: el uso del principio de "divide y vencerás". En términos del gráfico, esto conduce a la separación del conjunto de vértices en componentes débilmente conectados.

Permítame recordarle que el componente débilmente conectado es un subconjunto de vértices que es máximo en inclusión que entre dos cualesquiera existe una ruta desde los bordes en un gráfico no dirigido. Podemos obtener un gráfico no dirigido del original, por ejemplo, agregando el opuesto a cada borde (con eliminación posterior). Luego, un vértice de la conexión incluirá todos los vértices que podemos alcanzar cuando rodeamos el gráfico en profundidad.

Después de la separación de los componentes débilmente conectados, el gráfico tomará la siguiente forma:



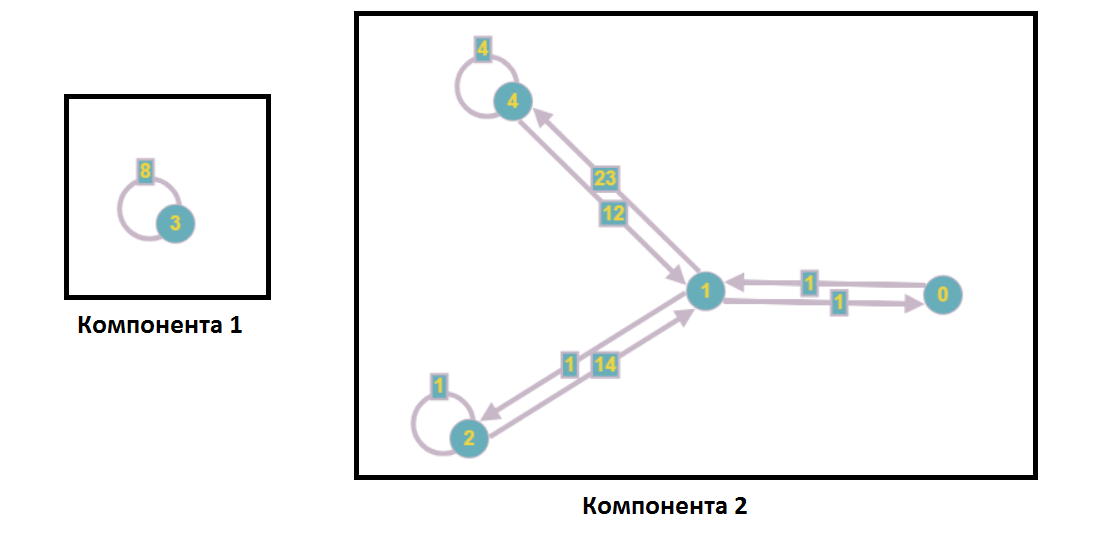
Como parte del análisis de un sistema de ecuaciones lineales, esto significa que no se incluye ningún vértice del primer componente en las ecuaciones con los números del segundo componente y viceversa, es decir, podemos resolver estos subsistemas de forma independiente (por ejemplo, en paralelo).

Reducción del vértice gráfico

El siguiente paso del algoritmo es exactamente qué es la optimización para trabajar con matrices dispersas. Incluso en el gráfico del ejemplo hay picos "colgantes", lo que significa que algunas de las ecuaciones incluyen solo un desconocido y, como sabemos, el valor de este desconocido es fácil de encontrar.

Para determinar tales ecuaciones, se propone almacenar una matriz de listas que contienen el número de variables incluidas en la ecuación que tienen el número de este elemento de matriz. Luego, cuando la lista alcanza el tamaño de la unidad, podemos reducir el vértice "solo" e informar al resto de las ecuaciones en las otras ecuaciones en las que entra este vértice.

Por lo tanto, podemos reducir el vértice 3 del ejemplo inmediatamente después de procesar completamente el componente:

$$

$$8⋅_3 = 4⇒_3 = 1/2$$

Procedemos de manera similar con la ecuación 0, ya que contiene solo una variable:

$$

$$1⋅x_1 = 1⇒x_1 = 1$$

Otras ecuaciones también cambiarán después de encontrar este resultado:

$$$$ display $$ 1⋅_1 ​​+ 1⋅_2 = 3⇒1⋅_2 = 3-1 = 2 $$ display $$

El gráfico toma la siguiente forma:



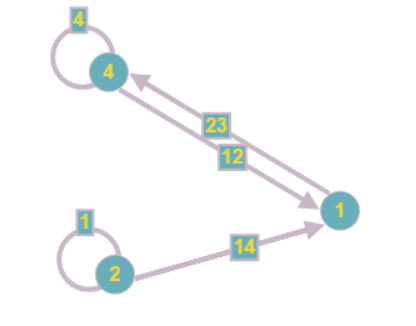
Tenga en cuenta que al reducir un vértice, también pueden aparecer otros que también contienen uno desconocido. Por lo tanto, este paso del algoritmo debe repetirse hasta que al menos uno de los vértices pueda reducirse.

Reconstrucción de gráficos

Los lectores más atentos podrían notar que es posible una situación en la que cada uno de los vértices del gráfico tendrá un grado de ocurrencia de al menos dos y será imposible continuar reduciendo constantemente los vértices.

El ejemplo más simple de tal gráfico: cada vértice tiene un grado de ocurrencia igual a dos, ninguno de los vértices se puede reducir.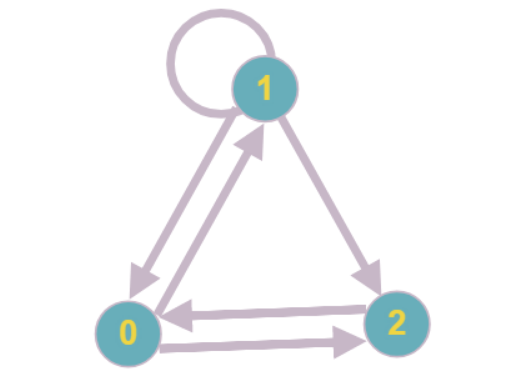



Como parte de la optimización para matrices dispersas, se supone que tales subgrafías serán de tamaño pequeño, sin embargo, aún debe trabajar con ellas. Para calcular los valores de las incógnitas que forman parte del subsistema de ecuaciones, se propone utilizar métodos clásicos para resolver SLAEs (es por eso que la introducción indica que para una matriz en la que todos o casi todos los coeficientes en las ecuaciones son distintos de cero, nuestro algoritmo tendrá la misma complejidad asintótica que los estándares). )

Por ejemplo, puede devolver el conjunto de vértices restantes después de la reducción a la forma de matriz y aplicarle el método de Gauss para resolver SLAE . Por lo tanto, obtendremos la solución exacta, y la velocidad del algoritmo se reducirá debido a que no se procesa todo el sistema, sino solo una parte de él.

Prueba de algoritmo

Para probar la implementación de software del algoritmo, tomamos varios sistemas reales de ecuaciones de gran volumen, así como una gran cantidad de sistemas generados aleatoriamente.
La generación de un sistema aleatorio de ecuaciones pasó por la adición secuencial de bordes de peso arbitrario entre dos vértices aleatorios. En total, el sistema estaba lleno del 5-10%. La corrección de las soluciones se verificó sustituyendo las respuestas obtenidas en el sistema original de ecuaciones.


Los sistemas oscilaron entre 1,000 y 200,000 incógnitas

Para comparar el rendimiento, utilizamos las bibliotecas más populares para resolver problemas de álgebra lineal, como superlu y lapack. Por supuesto, estas bibliotecas se centran en resolver una amplia clase de problemas y la solución de SLAE en ellas no está optimizada de ninguna manera, por lo que la diferencia de velocidad resultó ser significativa.


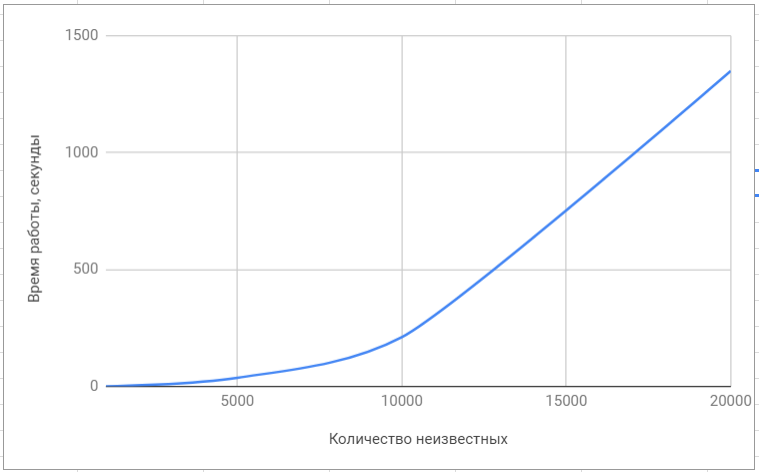Probar la biblioteca lapack


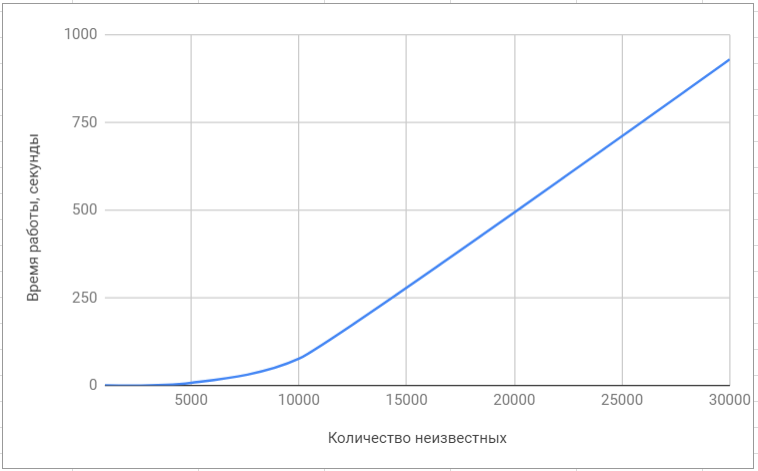Probar la biblioteca 'superlu'

Aquí está la comparación final de nuestro algoritmo con los algoritmos implementados en bibliotecas populares:

Conclusión

Incluso si no es un desarrollador de configuración 1C: Enterprise, las ideas y los métodos de optimización descritos en este artículo pueden ser utilizados por usted no solo al implementar un algoritmo para resolver SLAEs, sino también para toda una clase de problemas de álgebra lineal asociados con matrices.

Para los desarrolladores de 1C, agregamos que la nueva funcionalidad de la solución SLAE admite el uso paralelo de los recursos informáticos, y puede ajustar la cantidad de hilos de cálculo utilizados.