Descripción general del algoritmo de entrevista de trabajo: generación de conjuntos

Hola Habr!

Esta publicación comienza el análisis de tareas sobre los algoritmos que a las grandes empresas de TI (Mail.Ru Group, Google, etc.) les encanta dar candidatos para entrevistas (si la entrevista con algoritmos no es buena, entonces las posibilidades de conseguir un trabajo en una empresa soñada, por desgracia tienden a cero). En primer lugar, esta publicación es útil para aquellos que no tienen la experiencia de la programación de olimpiadas o cursos pesados ​​como ShAD o LKS, en los que los temas de los algoritmos se toman lo suficientemente en serio, o para aquellos que desean actualizar sus conocimientos en un campo determinado.

Al mismo tiempo, no se puede argumentar que todas las tareas que se tratarán aquí se cumplirán en la entrevista, sin embargo, los enfoques mediante los cuales se resuelven esas tareas son similares en la mayoría de los casos.

La narración se dividirá en diferentes temas, y comenzaremos generando conjuntos con una estructura específica.

1. Comencemos con el acordeón de botones: debe generar todas las secuencias de paréntesis correctas con paréntesis del mismo tipo ( cuál es la secuencia de paréntesis correcta ), donde el número de paréntesis es k.

Este problema puede resolverse de varias maneras. Comencemos con recursivo .

Este método supone que estamos comenzando a iterar sobre secuencias de una lista vacía. Después de agregar el corchete (apertura o cierre) a la lista, la llamada de recursión se realiza nuevamente y se verifican las condiciones. Cuales son las condiciones? Es necesario controlar la diferencia entre abrir y cerrar corchetes (variable cnt ): no puede agregar un corchete de cierre a la lista si esta diferencia no es positiva; de lo contrario, la secuencia de corchetes dejará de ser correcta. Queda por implementar cuidadosamente esto en el código.

 k = 6 #   init = list(np.zeros(k)) #  ,    cnt = 0 #    ind = 0 # ,       def f(cnt, ind, k, init): #  . ,     if (cnt <= k-ind-2): init[ind] = '(' f(cnt+1, ind+1, k, init) # .    ,  cnt > 0 if cnt > 0: init[ind] = ')' f(cnt-1, ind+1, k, init) #      if ind == k: if cnt == 0: print (init) 

La complejidad de este algoritmo es $$$O ((C_k ^ {k / 2} - C_k ^ {k / 2 -1}) * k)$memoria adicional requerida $$$O (k)$.

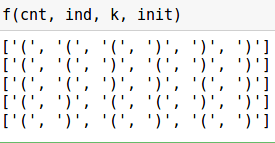
Con los parámetros dados, la llamada a la función $$$f (cnt, ind, k, init)$dará como resultado lo siguiente:

Una forma iterativa de resolver este problema: en este caso, la idea será fundamentalmente diferente: debe introducir el concepto de orden lexicográfico para las secuencias de paréntesis.

Todas las secuencias de paréntesis correctas para un tipo de paréntesis se pueden ordenar teniendo en cuenta el hecho de que $$$'(' <')'$. Por ejemplo, para n = 6, la secuencia más lexicográficamente más baja es $$$((()))$y el más viejo $$$() () ()$.

Para obtener la siguiente secuencia lexicográfica, debe encontrar el corchete de apertura más a la derecha, antes del cual hay un corchete de cierre, para que cuando se intercambien, la secuencia del corchete permanezca correcta. Los intercambiamos y hacemos que el sufijo sea el menor más lexicográfico; para esto, debe calcular en cada paso la diferencia entre el número de paréntesis.

En mi opinión, este enfoque es un poco lúgubre que recursivo, pero puede usarse para resolver otros problemas de generación de conjuntos. Implementamos esto en el código.

 #  ,    n = 6 arr = ['(' for _ in range(n//2)] + [')' for _ in range(n//2)] def f(n, arr): #    print (arr) while True: ind = n-1 cnt = 0 #  . ,    while ind>=0: if arr[ind] == ')': cnt -= 1 if arr[ind] == '(': cnt += 1 if cnt < 0 and arr[ind] =='(': break ind -= 1 #   ,     if ind < 0: break #   .  arr[ind] = ')' #      for i in range(ind+1,n): if i <= (n-ind+cnt)/2 +ind: arr[i] = '(' else: arr[i] = ')' print (arr) 

La complejidad de este algoritmo es la misma que en el ejemplo anterior.

Por cierto, hay un método simple que demuestra que el número de secuencias de paréntesis generadas para un n / 2 dado debe coincidir con los números catalanes .

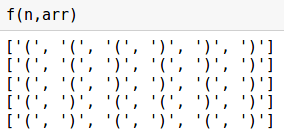
Funciona!

Genial, con los corchetes por ahora, pasemos a generar subconjuntos. Comencemos con un simple rompecabezas.

2. Dada una matriz de orden ascendente con números de $$$0$antes $$$n-1$, se requiere generar todos sus subconjuntos.

Tenga en cuenta que el número de subconjuntos de dicho conjunto es exactamente $$$2 ^ n$. Si cada subconjunto se representa como una matriz de índices, donde $$$0$significa que el elemento no está incluido en el conjunto, pero $$$1$- lo que está incluido, entonces la generación de todos estos arreglos será la generación de todos los subconjuntos.

Si consideramos la representación en bits de los números del 0 al $$$2 ^ n - 1$, luego especificarán los subconjuntos deseados. Es decir, para resolver el problema, es necesario implementar la adición de la unidad a un número binario. Comenzamos con todos los ceros y terminamos con una matriz en la que hay una unidad.

 n = 3 B = np.zeros(n+1) #  B   1  (    ) a = np.array(list(range(n))) #   def f(B, n, a): #   while B[0] == 0: ind = n #     while B[ind] == 1: ind -= 1 #   1 B[ind] = 1 #      B[(ind+1):] = 0 print (a[B[1:].astype('bool')]) 

La complejidad de este algoritmo es $$$O (n * 2 ^ n)$, de memoria - $$$O (n)$.

Ahora vamos a complicar un poco la tarea anterior.

3. Dada una matriz ordenada en orden ascendente con números de $$$0$antes $$$n-1$, necesitas generarlo todo $$$k$-conjuntos de elementos (resueltos de forma iterativa).

Observo que la formulación de este problema es similar a la anterior y se puede resolver utilizando aproximadamente la misma metodología: tome la matriz inicial con $$$k$unidades y $$$n-k$ceros e iterar sobre todas las variantes de tales secuencias en longitud $$$n.$

Sin embargo, se requieren cambios menores. Necesitamos clasificar todo $$$k$-valorizados conjuntos de números de $$$0$antes $$$n-1$. Debe comprender exactamente cómo debe ordenar los subconjuntos. En este caso, podemos introducir el concepto de orden lexicográfico para tales conjuntos.

También organizamos la secuencia por códigos de caracteres: $$$1 <0$(Esto, por supuesto, es extraño, pero es necesario, y ahora entenderemos por qué). Por ejemplo, para $$$n = 4, k = 2$el más joven y el más viejo será la secuencia $$$[1,1,0,0]$y $$$[0,0,1,1]$.

Queda por comprender cómo describir la transición de una secuencia a otra. Aquí todo es simple: si cambiamos $$$1$en $$$0$, luego a la izquierda escribimos el mínimo lexicográfico teniendo en cuenta la preservación de la condición en $$$k$. Código:

 n = 5 k = 3 a = np.array(list(range(n))) #    k -   init = [1 for _ in range(k)] + [0 for _ in range(nk)] def f(a, n, k, init): #   k-  print (a[a[init].astype('bool')]) while True: unit_cnt = 0 cur_ind = 0 #   ,     1 while (cur_ind < n) and (init[cur_ind]==1 or unit_cnt==0): if init[cur_ind] == 1: unit_cnt += 1 cur_ind += 1 #        -    if cur_ind == n: break #  init[cur_ind] = 1 #   . .  for i in range(cur_ind): if i < unit_cnt-1: init[i] = 1 else: init[i] = 0 print (a[a[init].astype('bool')]) 

Ejemplo de trabajo:

La complejidad de este algoritmo es $$$O (C_n ^ k * n)$, de memoria - $$$O (n)$.

4. Dada una matriz de orden ascendente con números de $$$0$antes $$$n-1$, necesitas generarlo todo $$$k$-conjuntos de elementos (resolver recursivamente).

Ahora intentemos la recursividad. La idea es simple: esta vez sin una descripción, vea el código.

 n = 5 a = np.array(list(range(n))) ind = 0 # ,       num = 0 # ,       k = 3 sub = list(-np.ones(k)) #  def f(n, a, num, ind, k, sub): #   k  ,     if ind == k: print (sub) else: for i in range(n - num): #  ,      k  if (n - num - i >= k - ind): #      sub[ind] = a[num + i] #     f(n, a, num+1+i, ind+1, k, sub) 

Ejemplo de trabajo:

La complejidad es la misma que en el método anterior.

5. Dada una matriz de orden ascendente con números de $$$0$antes $$$n-1$, se requiere para generar todas sus permutaciones.

Resolveremos usando la recursividad. La solución es similar a la anterior, donde tenemos una lista auxiliar. Inicialmente es cero si está activado $$$i$-el lugar del elemento es una unidad, entonces el elemento $$$i$Ya en la permutación. Apenas dicho que hecho:

 a = np.array(range(3)) n = a.shape[0] ind_mark = np.zeros(n) #   perm = -np.ones(n) #     def f(ind_mark, perm, ind, n): if ind == n: print (perm) else: for i in range(n): if not ind_mark[i]: #     ind_mark[i] = 1 #   perm[ind] = i f(ind_mark, perm, ind+1, n) #   -    ind_mark[i] = 0 

Ejemplo de trabajo:

La complejidad de este algoritmo es $$$O (n ^ 2 * n!)$, de memoria - $$$O (n).$

Ahora considere dos rompecabezas muy interesantes para los códigos Gray . En pocas palabras, este es un conjunto de secuencias de la misma longitud, donde cada secuencia difiere de sus vecinos en una categoría.

6. Genere todos los códigos grises bidimensionales de longitud n.

La idea de resolver este problema es genial, pero si no conoce la solución, puede ser muy difícil de pensar. Observo que el número de tales secuencias es $$$2 ^ n$.

Resolveremos iterativamente. Supongamos que generamos alguna parte de tales secuencias y se encuentran en alguna lista. Si duplicamos dicha lista y la escribimos en el orden inverso, entonces la última secuencia de la primera lista coincide con la primera secuencia de la segunda lista, la penúltima coincide con la segunda, etc. Combina estas listas en una.

¿Qué debe hacerse para que todas las secuencias de la lista difieran entre sí en la misma categoría? Coloque una unidad en los lugares apropiados en los elementos de la segunda lista para obtener los códigos grises.

Es difícil de percibir "de oído", representaremos iteraciones de este algoritmo.

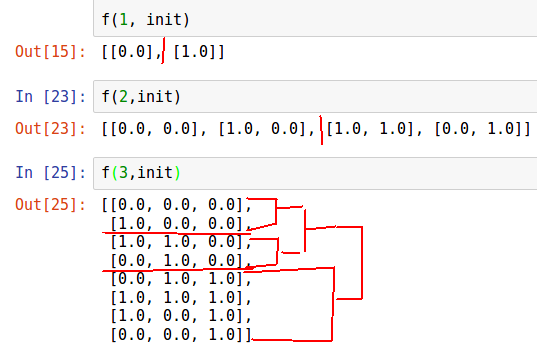
 n = 3 init = [list(np.zeros(n))] def f(n, init): for i in range(n): for j in range(2**i): init.append(list(init[2**i - j - 1])) init[-1][i] = 1.0 return init 

La complejidad de esta tarea es $$$O (n * 2 ^ n)$, de memoria lo mismo.

Ahora vamos a complicar la tarea.

7. Genere todos los códigos grises k-dimensionales de longitud n.

Está claro que la tarea pasada es solo un caso especial de esta tarea. Sin embargo, de la hermosa manera en que se resolvió la tarea pasada, esto no se puede resolver; aquí es necesario ordenar las secuencias en el orden correcto. Vamos a obtener una matriz bidimensional $$$k * n$. Inicialmente, la última línea tiene unidades, y el resto tiene ceros. Además, en la matriz, $$$-1$. Aqui $$$1$y $$$-1$difieren entre sí en la dirección: $$$1$señala $$$-1$apunta hacia abajo. Importante: en cada columna en cualquier momento solo puede haber uno $$$1$o $$$-1$, y los números restantes serán ceros.

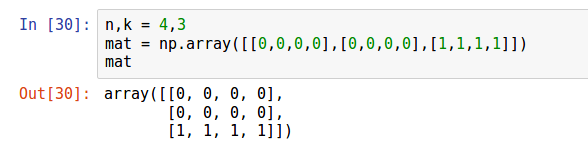
Ahora entenderemos cómo es posible ordenar estas secuencias para obtener códigos Gray. Comience desde el final para mover el elemento hacia arriba.

En el siguiente paso, llegamos al techo. Escribimos la secuencia resultante. Después de alcanzar el límite, debe comenzar a trabajar con la siguiente columna. Debe buscarlo de derecha a izquierda, y si encontramos una columna que se puede mover, entonces, para todas las columnas con las que no podríamos trabajar, las flechas cambiarán en la dirección opuesta para que puedan moverse nuevamente.

Ahora puede mover la primera columna hacia abajo. Lo movemos hasta que toque el piso. Y así sucesivamente, hasta que todas las flechas toquen el piso o el techo y no queden columnas que puedan moverse.

Sin embargo, en el marco del ahorro de memoria, resolveremos este problema utilizando dos matrices unidimensionales de longitud $$$n$: en una matriz, los elementos de la secuencia mismos se ubicarán, y en la otra dirección (flechas).

 n,k = 3,3 arr = np.zeros(n) direction = np.ones(n) #   ,    def k_dim_gray(n,k): #    print (arr) while True: ind = n-1 while ind >= 0: #    ,    if (arr[ind] == 0 and direction[ind] == 0) or (arr[ind] == k-1 and direction[ind] == 1): direction[ind] = (direction[ind]+1)%2 else: break ind -= 1 #     ,     if ind < 0: break #    1 ,   1  arr[ind] += direction[ind]*2 - 1 print (arr) 

Ejemplo de trabajo:

La complejidad del algoritmo es $$$O (n * k ^ n)$, de memoria - $$$O (n)$.

La exactitud de este algoritmo se demuestra por inducción en $$$n$Aquí no describiré la evidencia.

En la próxima publicación analizaremos las tareas para la dinámica.