Cálculo de integrales definidas: algoritmos básicos

Esta publicación describe los métodos más simples para calcular las integrales de funciones de una variable en un segmento, también llamadas fórmulas de cuadratura. Por lo general, estos métodos se implementan en bibliotecas matemáticas estándar, como la Biblioteca científica GNU para C, SciPy para Python y otras. La publicación tiene como objetivo demostrar cómo funcionan estos métodos "bajo el capó" y llamar la atención sobre algunos problemas de precisión y rendimiento de los algoritmos. También me gustaría señalar la relación de las fórmulas en cuadratura y los métodos de integración numérica de las ecuaciones diferenciales ordinarias, sobre las cuales quiero escribir otra publicación.

Definición de la integral

Integral (según Riemann) de una función $$$f (x)$ en el segmento $$$[a; b]$ El siguiente límite se llama:

donde $$$\ Delta x = \ max \ lbrace x_ {i + 1} - x_i \ rbrace$ - finura de la partición, $$$x_0 = a$ , $$$x_n = b$ , $$$\ xi_i$ - un número arbitrario en el segmento $$$[x_i; x_ {i + 1}]$ .

Si existe la integral de la función, entonces el valor límite es el mismo independientemente de la partición, si solo fuera lo suficientemente pequeño.

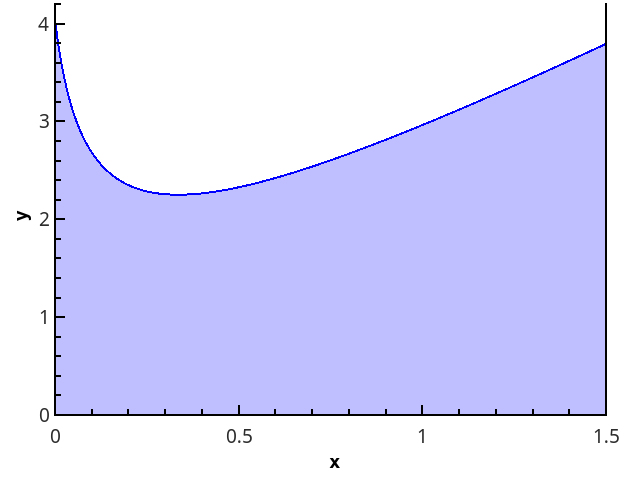
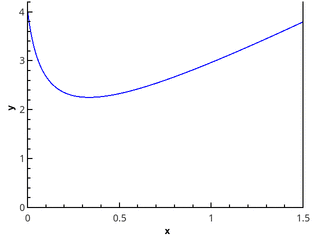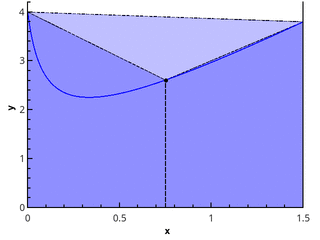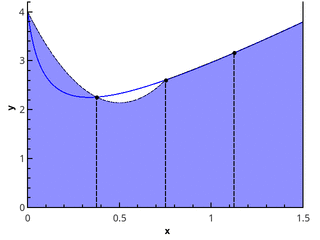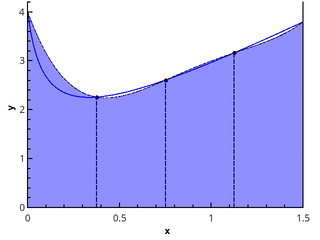
La definición geométrica es más clara: la integral es igual al área del trapecio curvado delimitado por el eje 0 x , el gráfico de la función y las líneas rectas x = a y x = b (región rellena en la figura).

Fórmulas de cuadratura

La definición de integral (1) se puede reescribir en la forma

donde $$$w_i$ - coeficientes de ponderación, cuya suma debe ser igual a 1, y los coeficientes en sí mismos - tienden a cero con un número creciente $$$n$ puntos en los que se calcula la función.

La expresión (2) es la base de todas las fórmulas de cuadratura (es decir, fórmulas para el cálculo aproximado de la integral). El desafío es seleccionar puntos $$$\ lbrace \ xi_i \ rbrace$ y peso $$$w_i$ de modo que la suma en el lado derecho se aproxima a la integral requerida con la mayor precisión posible.

Tarea computacional

Conjunto de funciones $$$f (x)$ para lo cual existe un algoritmo para calcular valores en cualquier punto del intervalo $$$[a; b]$ (Me refiero a los puntos representados por un número de coma flotante, ¡no hay funciones de Dirichlet allí!).

Se requiere encontrar el valor aproximado de la integral $$$\ int_a ^ b f (x) dx$ .
Las soluciones se implementarán en Python 3.6.

Para verificar los métodos, use la integral $$$\ int_0 ^ {3/2} \ left [2x + \ frac {1} {\ sqrt {x + 1/16}} \ right] dx = 17/4$ .

Aproximación constante por partes

Las fórmulas de cuadratura idealmente simples surgen de la aplicación de la expresión (1) "en la frente":

Porque del método de dividir un segmento por puntos $$$\ lbrace x_i \ rbrace$ y seleccione puntos $$$\ lbrace \ xi_i \ rbrace$ el valor límite no depende, entonces los elegimos para que puedan calcularse convenientemente; por ejemplo, tomamos la partición de manera uniforme y para los puntos del cálculo de la función consideramos las opciones: 1) $$$\ xi_i = x_i$ ; 2) $$$\ xi_i = x_ {i + 1}$ ; 3) $$$\ xi_i = (x_i + x_ {i + 1}) / 2$ .

Obtenemos los métodos de rectángulos izquierdos, rectángulos derechos y rectángulos con un punto medio, respectivamente.

def _rectangle_rule(func, a, b, nseg, frac): """  .""" dx = 1.0 * (b - a) / nseg sum = 0.0 xstart = a + frac * dx # 0 <= frac <= 1    , #    , #     dx for i in range(npoints): sum += func(xstart + i * dx) return sum * dx def left_rectangle_rule(func, a, b, nseg): """  """ return _rectangle_rule(func, a, b, nseg, 0.0) def right_rectangle_rule(func, a, b, nseg): """  """ return _rectangle_rule(func, a, b, npoints, 1.0) def midpoint_rectangle_rule(func, a, b, nseg): """    """ return _rectangle_rule(func, a, b, nseg, 0.5) 

Para analizar el rendimiento de las fórmulas en cuadratura, construimos una gráfica del error en las coordenadas "el número de puntos es la diferencia entre el resultado numérico y el exacto".

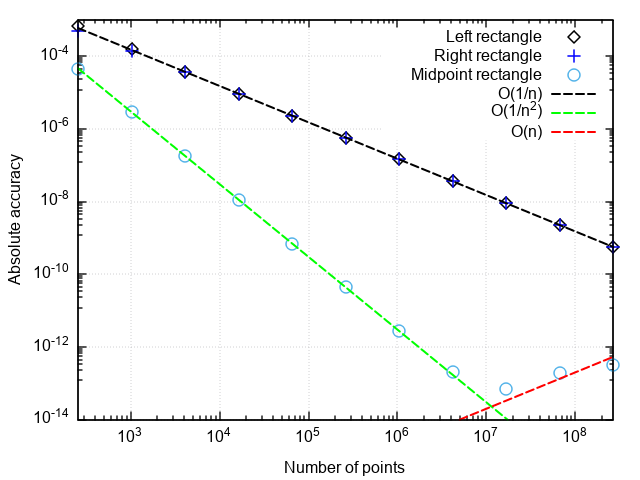
Lo que puedes notar:

1. Una fórmula con un punto medio es mucho más precisa que con un punto derecho o izquierdo
2. El error de la fórmula con el punto medio cae más rápido que los otros dos
3. Con una partición muy pequeña, el error de la fórmula con el punto medio comienza a aumentar
   Los primeros dos puntos están relacionados con el hecho de que la fórmula de los rectángulos con un punto medio tiene un segundo orden de aproximación, es decir. $$$| I_n - I | = O (1 / n ^ 2)$ , y las fórmulas de los rectángulos derecho e izquierdo son de primer orden, es decir $$$| I_n - I | = O (1 / n)$ .
   Un aumento en el error durante la rectificación del paso de integración se asocia con un aumento en el error de redondeo al sumar una gran cantidad de términos. Este error crece como $$$| I_n - I | = O (1 / n)$ eso no permite la integración para lograr la precisión de la máquina.
   Conclusión: los métodos de rectángulos con puntos derecho e izquierdo tienen baja precisión, que también crece lentamente con el refinamiento de la partición. Por lo tanto, solo tienen sentido para fines de demostración. El método de los rectángulos con un punto medio tiene un orden de aproximación más alto, lo que le da la oportunidad de ser utilizado en aplicaciones reales (más sobre eso a continuación).

Aproximación lineal por partes

El siguiente paso lógico es aproximar la función integrable en cada uno de los subsegmentos mediante una función lineal, que proporciona la fórmula en cuadratura de los trapecios:

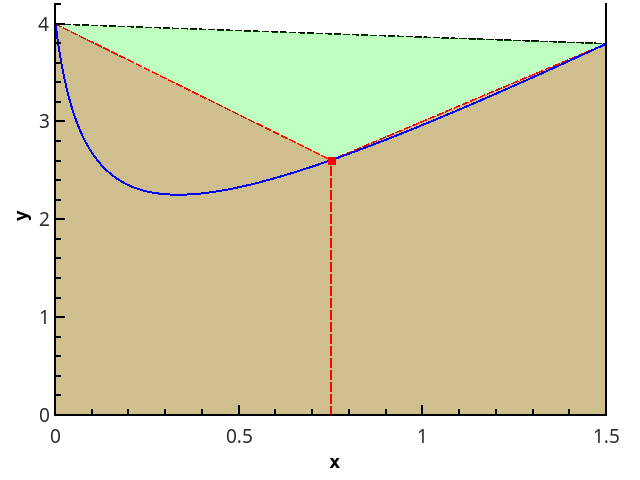
Ilustración del método trapezoidal para n = 1 yn = 2.

En el caso de una cuadrícula uniforme, las longitudes de todos los segmentos de la partición son iguales, y la fórmula tiene la forma

 def trapezoid_rule(func, a, b, nseg): """  nseg -  ,    [a;b]""" dx = 1.0 * (b - a) / nseg sum = 0.5 * (func(a) + func(b)) for i in range(1, nseg): sum += func(a + i * dx) return sum * dx 

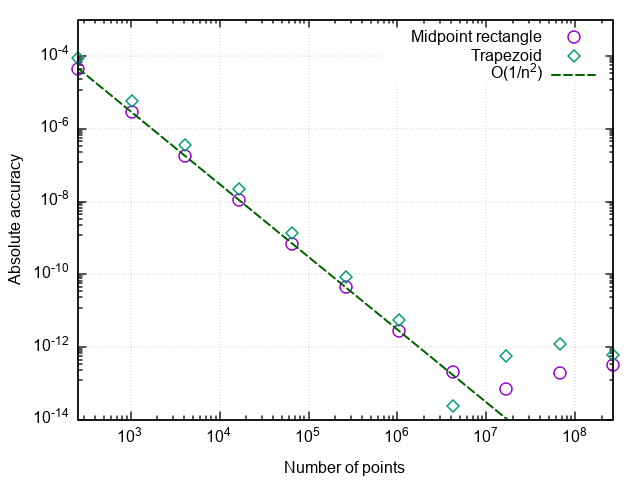
Después de trazar el error versus el número de puntos divididos, vemos que el método trapezoidal también tiene un segundo orden de aproximación y generalmente da resultados ligeramente diferentes del método del rectángulo del punto medio (en adelante, simplemente el método del rectángulo).

Control de precisión de cálculo

Establecer el número de puntos divididos como un parámetro de entrada no es muy práctico, ya que generalmente se requiere calcular la integral no con una densidad de partición dada, sino con un error dado. Si el integrando se conoce de antemano, entonces podemos estimar el error de antemano y elegir un paso de integración de tal manera que se logre la precisión especificada. Pero esto rara vez es el caso en la práctica (y, en general, ¿no es más fácil, con la función conocida de antemano, integrar la integral por adelantado?), Por lo tanto, es necesario un procedimiento para ajustar automáticamente el paso a un error dado.

¿Cómo implementar esto? Uno de los métodos simples para estimar el error, la regla Runge , la diferencia en los valores de las integrales calculados a partir de n y 2 n puntos, proporciona una estimación de error: $$$\ Delta_ {2n} \ aprox | I_ {2n} - I_n |$ . El método trapezoidal es más conveniente para duplicar la finura de una partición que el método de rectángulos con un punto central. Al calcular mediante el método trapezoidal, para duplicar el número de puntos, solo se necesitan nuevos valores de la función en el medio de los segmentos de la partición anterior, es decir, la aproximación previa de la integral se puede usar para calcular la siguiente.

Desde aquí obtenemos el siguiente código para el método trapezoidal con control de precisión:

 def trapezoid_rule(func, a, b, rtol = 1e-8, nseg0 = 1): """  rtol -     nseg0 -    """ nseg = nseg0 old_ans = 0.0 dx = 1.0 * (b - a) / nseg ans = 0.5 * (func(a) + func(b)) for i in range(1, nseg): ans += func(a + i * dx) ans *= dx err_est = max(1, abs(ans)) while (err_est > abs(rtol * ans)): old_ans = ans ans = 0.5 * (ans + midpoint_rectangle_rule(func, a, b, nseg)) #      #       nseg *= 2 err_est = abs(ans - old_ans) return ans 

Con este enfoque, el integrando no se calculará varias veces en un punto, y todos los valores calculados se utilizan para el resultado final.

Pero, ¿es posible lograr una mayor precisión con el mismo número de cálculos de funciones? Resulta que es posible, hay fórmulas que funcionan con mayor precisión que el método trapezoidal en la misma cuadrícula.

Aproximación parabólica por partes

El siguiente paso es aproximar la función con elementos parabólicos. Esto requiere que el número de segmentos de la partición sea par, luego se pueden dibujar parábolas a través de triples de puntos con abscisas {( x ₀ = a , x ₁ , x ₂ ), ( x ₂ , x ₃ , x ₄ ), ..., ( x _{n -2} , x _{n -1} , x _n = b )}.

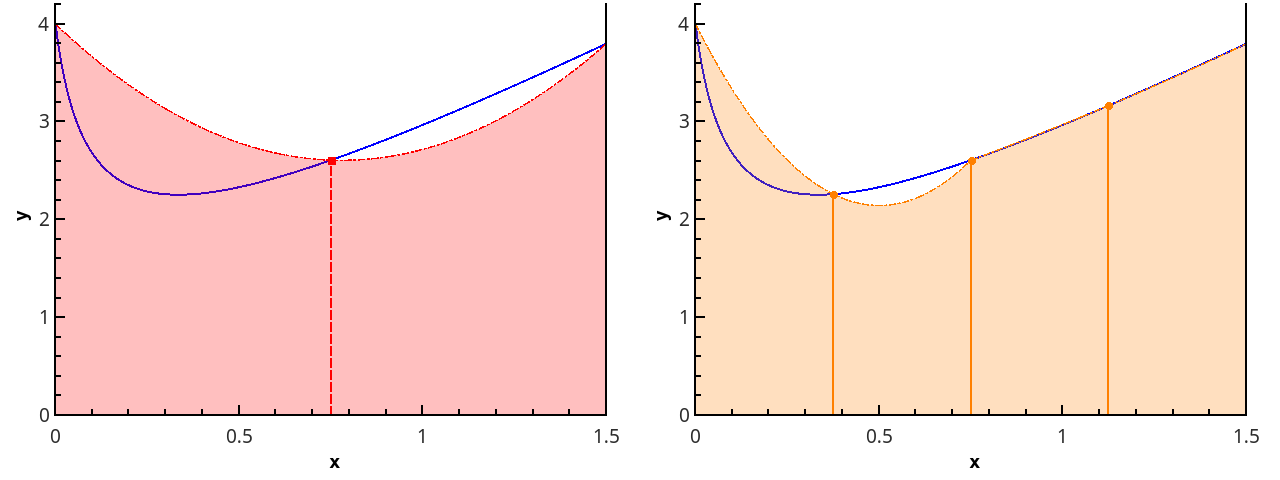
Ilustración de una aproximación parabólica por partes en 3 y 5 puntos ( n = 2 yn = 3).

Acercarse a la integral de la función en cada uno de los segmentos [ x _k ; x _{k +2} ] por la integral de la aproximación parabólica en este segmento y suponiendo que los puntos se distribuyan uniformemente ( x _{k +1} = x _k + h ), obtenemos la fórmula de Simpson :

La fórmula (4) produce directamente una implementación "ingenua" del método Simpson:

 def simpson_rule(func, a, b, nseg): """  nseg -  ,    [a;b]""" if nseg%2 = 1: nseg += 1 dx = 1.0 * (b - a) / nseg sum = (func(a) + 4 * func(a + dx) + func(b)) for i in range(1, nseg / 2): sum += 2 * func(a + (2 * i) * dx) + 4 * func(a + (2 * i + 1) * dx) return sum * dx / 3 

Para estimar el error, puede usar el mismo cálculo de la integral con los pasos h y h / 2, pero aquí está el problema, al calcular la integral con un paso más pequeño, el resultado del cálculo anterior deberá descartarse, aunque la mitad de los cálculos de la nueva función estarán en los mismos puntos que antes.

Afortunadamente, puede evitar perder el tiempo de la máquina si implementa el método Simpson de una manera más ingeniosa. Después de mirar más de cerca, notamos que la integral por la fórmula de Simpson se puede representar a través de dos integrales por la fórmula trapezoidal con diferentes pasos. Esto se ve más claramente en el caso básico de aproximación de la integral en tres puntos. $$$(a, f_0), ~ (a + h, f_1), ~ (a + 2h, f_2)$ :

Por lo tanto, si implementamos el procedimiento de reducir el paso a la mitad y almacenamos los dos últimos cálculos mediante el método trapezoidal, el método Simpson con control de precisión se implementa de manera más eficiente.

 class Quadrature: """    """ __sum = 0.0 __nseg = 1 #    __ncalls = 0 #      def __restart(func, x0, x1, nseg0, reset_calls = True): """    .       """ if reset_calls: Quadrature.__ncalls = 0 Quadrature.__nseg = nseg0 #           nseg0 Quadrature.__sum = 0.5 * (func(x0) + func(x1)) dx = 1.0 * (x1 - x0) / nseg0 for i in range(1, nseg0): Quadrature.__sum += func(x0 + i * dx) Quadrature.__ncalls += 1 + nseg0 return Quadrature.__sum * dx def __double_nseg(func, x0, x1): """  .       """ nseg = Quadrature.__nseg dx = (x1 - x0) / nseg x = x0 + 0.5 * dx i = 0 AddedSum = 0.0 for i in range(nseg): AddedSum += func(x + i * dx) Quadrature.__sum += AddedSum Quadrature.__nseg *= 2 Quadrature.__ncalls += nseg return Quadrature.__sum * 0.5 * dx def trapezoid(func, x0, x1, rtol = 1e-10, nseg0 = 1): """     . rtol -  , nseg0 -    """ ans = Quadrature.__restart(func, x0, x1, nseg0) old_ans = 0.0 err_est = max(1, abs(ans)) while (err_est > abs(rtol * ans)): old_ans = ans ans = Quadrature.__double_nseg(func, x0, x1) err_est = abs(old_ans - ans) print("Total function calls: " + str(Quadrature.__ncalls)) return ans def simpson(func, x0, x1, rtol = 1.0e-10, nseg0 = 1): """     . rtol -  , nseg0 -    """ old_trapez_sum = Quadrature.__restart(func, x0, x1, nseg0) new_trapez_sum = Quadrature.__double_nseg(func, x0, x1) ans = (4 * new_trapez_sum - old_trapez_sum) / 3 old_ans = 0.0 err_est = max(1, abs(ans)) while (err_est > abs(rtol * ans)): old_ans = ans old_trapez_sum = new_trapez_sum new_trapez_sum = Quadrature.__double_nseg(func, x0, x1) ans = (4 * new_trapez_sum - old_trapez_sum) / 3 err_est = abs(old_ans - ans) print("Total function calls: " + str(Quadrature.__ncalls)) return ans 

Compare la efectividad del método de trapecio y parábola:

 >>> import math >>> Quadrature.trapezoid(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9) Total function calls: 65537 4.250000001385811 >>> Quadrature.simpson(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9) Total function calls: 2049 4.2500000000490985 

Como puede ver, con ambos métodos se puede obtener la respuesta con una precisión bastante alta, pero el número de llamadas al integrando es muy diferente: ¡un método de orden superior es 32 veces más eficiente!

Al trazar el error de integración frente al número de pasos, podemos verificar que el orden de aproximación de la fórmula de Simpson es cuatro, es decir error de integración numérica $$$| I_ {Simps, n} - I | = O (1 / n ^ 4)$ (¡y las integrales de polinomios cúbicos que usan esta fórmula se calculan hasta errores de redondeo para cualquier par n > 0!).

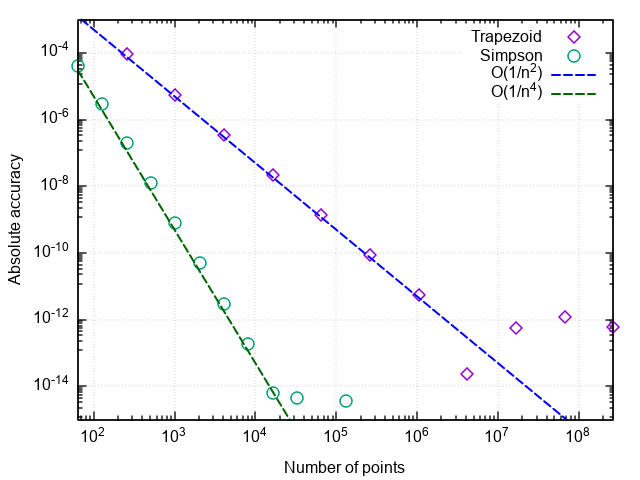
Por lo tanto, tal aumento en la eficiencia surge en comparación con la fórmula trapezoidal simple.

Que sigue

La lógica adicional de aumentar la precisión de las fórmulas de cuadratura es generalmente comprensible: si continuamos aproximando la función con polinomios de un grado cada vez mayor, entonces la integral de estos polinomios se aproximará cada vez con mayor precisión a la integral de la función original. Este enfoque se llama la construcción de fórmulas cuadráticas de Newton-Cotes . Se conocen fórmulas de hasta 8 órdenes de aproximación, pero los términos alternos aparecen entre los coeficientes de ponderación w _i en (2), y las fórmulas pierden estabilidad en los cálculos.

Probemos a la inversa. El error de la fórmula en cuadratura se representa como una serie en potencias del paso de integración h . Una propiedad notable del método trapezoidal (¡y rectángulos con un punto medio!) Es que, para él, esta serie consta solo de grados pares:

La extrapolación de Richardson se basa en encontrar aproximaciones sucesivas a esta expansión: en lugar de aproximar el integrando por un polinomio, a partir de las aproximaciones calculadas de la integral $$$I (h)$ se construye una aproximación polinómica, que para h = 0 debería dar la mejor aproximación al valor verdadero de la integral.

Ampliar el error de integración en potencias pares del paso de partición acelera bruscamente la convergencia de la extrapolación, porque para la aproximación del orden 2 n , el método trapezoide solo necesita n valores de la integral.

Si asumimos que cada término subsiguiente es menor que el anterior, entonces podemos excluir secuencialmente los grados de h , teniendo aproximaciones integrales calculadas con diferentes pasos. Dado que la implementación anterior nos permite dividir fácilmente la partición por la mitad, es conveniente considerar las fórmulas para los pasos h y h / 2.

Es fácil demostrar que la excepción del término principal del error de la fórmula trapezoidal dará exactamente la fórmula de Simpson:

Repitiendo un procedimiento similar para la fórmula de Simpson, obtenemos:

Si continúa, aparece la siguiente tabla:

La primera columna contiene las integrales calculadas por el método trapezoidal. Cuando se mueve desde la fila superior hacia abajo, la división del segmento se vuelve dos veces más pequeña, y cuando se mueve desde la columna izquierda hacia la derecha, el orden de aproximación de la integral aumenta (es decir, la segunda columna contiene las integrales por el método Simpson, etc.).

Los elementos de la tabla, como se puede deducir de la expansión (5), están relacionados por la relación de recurrencia:

El error de la aproximación de la integral se puede estimar a partir de la diferencia de fórmulas de diferentes órdenes en una línea, es decir.

El uso de la extrapolación de Richardson junto con la integración trapezoidal se llama método Romberg . Si el método Simpson toma en cuenta los dos valores anteriores por el método trapezoidal, el método Romberg usa todos los valores calculados previamente por el método trapezoidal para obtener una estimación más precisa de la integral.

 class Quadrature: """    """ __sum = 0.0 __nseg = 1 #    __ncalls = 0 #      def __restart(func, x0, x1, nseg0, reset_calls = True): """    .       """ if reset_calls: Quadrature.__ncalls = 0 Quadrature.__nseg = nseg0 #          nseg0  Quadrature.__sum = 0.5 * (func(x0) + func(x1)) dx = 1.0 * (x1 - x0) / nseg0 for i in range(1, nseg0): Quadrature.__sum += func(x0 + i * dx) Quadrature.__ncalls += 1 + nseg0 return Quadrature.__sum * dx def __double_nseg(func, x0, x1): """  .       """ nseg = Quadrature.__nseg dx = (x1 - x0) / nseg x = x0 + 0.5 * dx i = 0 AddedSum = 0.0 for i in range(nseg): AddedSum += func(x + i * dx) Quadrature.__sum += AddedSum Quadrature.__nseg *= 2 Quadrature.__ncalls += nseg return Quadrature.__sum * 0.5 * dx def romberg(func, x0, x1, rtol = 1e-10, nseg0 = 1, maxcol = 5, reset_calls = True): """   nseg0 -     maxcol -   """ #   Itable = [[Quadrature.__restart(func, x0, x1, nseg0, reset_calls)]] i = 0 maxcol = max(0, maxcol) ans = Itable[i][i] error_est = max(1, abs(ans)) while (error_est > abs(rtol * ans)): old_ans = ans i += 1 d = 4.0 ans_col = min(i, maxcol) Itable.append([Quadrature.__double_nseg(func, x0, x1)] * (ans_col + 1)) for j in range(0, ans_col): diff = Itable[i][j] - Itable[i - 1][j] Itable[i][j + 1] = Itable[i][j] + diff / (d - 1.0) d *= 4.0 ans = Itable[i][ans_col] if (maxcol <= 1): #       error_est = abs(ans - Itable[i - 1][-1]) elif (i > maxcol): error_est = abs(ans - Itable[i][min(i - maxcol - 1, maxcol - 1)]) else: error_est = abs(ans - Itable[i - 1][i - 1]) print("Total function calls: " + str(Quadrature.__ncalls)) return ans 

Veamos cómo funciona la aproximación de alto orden:

 >>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 0) #  Total function calls: 65537 4.250000001385811 >>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 1) #  Total function calls: 2049 4.2500000000490985 >>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 4) Total function calls: 257 4.250000001644076 

Estamos convencidos de que, en comparación con el método de la parábola, el número de llamadas al integrando ha disminuido otras 8 veces. Con un aumento adicional en la precisión requerida, las ventajas del método Romberg se vuelven aún más pronunciadas:

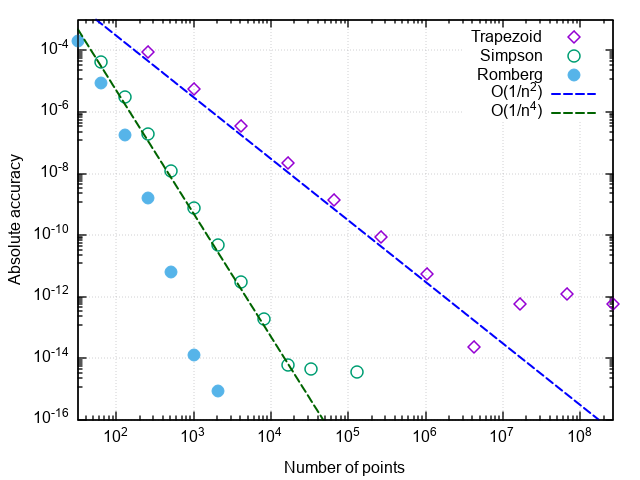
Algunas notas

Observación 1. El número de llamadas a funciones en estos problemas caracteriza el número de sumas al calcular la integral. Reducir el número de cálculos del integrando no solo ahorra recursos informáticos (aunque también es el caso de una implementación más optimizada), sino que también reduce el efecto de los errores de redondeo en el resultado. Entonces, cuando intenta calcular la integral de la función de prueba, el método trapezoidal se congela cuando intenta alcanzar una precisión relativa de 5 × ^10-15 , el método de parábola - con la precisión deseada de 2 × ^10-16 (que es el límite para números de doble precisión), y el método Romberg hace frente al cálculo prueba integral hasta la precisión de la máquina (con un error de bit bajo) Es decir, no solo se aumenta la precisión de la integración para un número dado de llamadas de función, sino también la precisión máxima alcanzable del cálculo de la integral.

Observación 2. Si el método converge cuando se especifica una cierta precisión, esto no significa que el valor calculado de la integral tenga la misma precisión. En primer lugar, esto se aplica a los casos en que el error especificado está cerca de la precisión de la máquina.

Observación 3. Aunque el método Romberg para una serie de funciones funciona de una manera casi mágica, se supone que el integrando tiene derivados acotados de órdenes altas. Esto significa que para funciones con torceduras o interrupciones, puede resultar peor que los métodos simples. Por ejemplo, integre f ( x ) = | x |:

 >>> Quadrature.trapezoid(abs, -1, 3, rtol=1e-5) Total function calls: 9 5.0 >>> Quadrature.simpson(abs, -1, 3, rtol=1e-5) Total function calls: 17 5.0 >>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 2) Total function calls: 17 5.0 >>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 3) Total function calls: 33 5.0 >>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 4) Total function calls: 33 5.000001383269357 

Observación 4. Puede parecer que cuanto mayor sea el orden de aproximación, mejor. De hecho, es mejor limitar el número de columnas en la tabla de Romberg a 4-6. Para entender esto, mira la fórmula (6). El segundo término es la diferencia de dos elementos consecutivos de la j -1ª columna dividida por aproximadamente 4 ^j . Porque la j -ésima columna contiene aproximaciones de una integral de orden 2 j , entonces la diferencia en sí misma es del orden de (1 / n _i ) ^{2 j} ~ 4 ^{- ij} . Teniendo en cuenta la división, ^se obtiene ~ 4 ^{- ( i +1) j} ~ 4 ^{- j 2} . Es decir para j ~ 7, el segundo término en (6) pierde precisión después de la reducción de las órdenes al agregar números de punto flotante, y un aumento en el orden de aproximación puede conducir a la acumulación de errores de redondeo.

Observación 5. Las partes interesadas pueden usar los métodos descritos para encontrar la integral por interés. $$$\ int_0 ^ 1 \ sqrt {x} \ sin {x} dx$ y equivalente a él $$$\ int_0 ^ 1 2t ^ 2 \ sin {t ^ 2} dt$ . Como dicen, siente la diferencia.

Conclusión

Se presenta la descripción e implementación de los métodos básicos de integración numérica de funciones en una cuadrícula uniforme. Se demuestra cómo, utilizando una modificación simple, obtener la clase de fórmulas en cuadratura utilizando el método de Romberg sobre la base del método trapezoidal, que acelera significativamente la convergencia de la integración numérica. El método funciona bien para integrar funciones "ordinarias", es decir variando débilmente en el intervalo de integración, no teniendo singularidades en los bordes del segmento (ver Observación 5), oscilaciones rápidas, etc.

( [3] — C++).

1. .. , .. . . .: . 1989.
2. J. Stoer, R. Bulirsch. Introduction to Numerical Analysis: Second Edition. Springer-Verlag New York. 1993.
3. WH Press, SA Teukolsky, WT Vetterling, BP Flannery. Numerical Recipes: Third Edition. Cambridge University Press. 2007.