Luché con la tentación de nombrar el artículo algo así como "La aterradora ineficiencia de los algoritmos STL", ya sabes, solo por el entrenamiento en el arte de crear titulares llamativos. Sin embargo, decidió permanecer dentro de los límites de la decencia: es mejor recibir comentarios de los lectores sobre el contenido del artículo que indignación por su gran nombre.
En este punto, supondré que conoce un poco de C ++ y STL, y también se encargará de los algoritmos utilizados en su código, su complejidad y relevancia para las tareas.
Algoritmos
Uno de los consejos bien conocidos que puede escuchar de la comunidad moderna de desarrolladores de C ++ no es idear bicicletas, sino utilizar algoritmos de la biblioteca estándar. Este es un buen consejo. Estos algoritmos son seguros, rápidos y probados a lo largo de los años. También a menudo doy consejos sobre cómo aplicarlos.
Cada vez que desee escribir otro, primero debe recordar si hay algo en el STL (o impulso) que ya resuelve este problema en una línea. Si lo hay, a menudo es mejor usar esto. Sin embargo, en este caso, también debemos entender qué tipo de algoritmo subyace a la llamada de la función estándar, cuáles son sus características y limitaciones.
Por lo general, si nuestro problema coincide exactamente con la descripción del algoritmo de STL, sería una buena idea tomarlo y aplicarlo "frente". El único problema es que los datos no siempre se almacenan en la forma en que el algoritmo implementado en la biblioteca estándar quiere recibirlos. Entonces podemos tener la idea de convertir primero los datos y luego aplicar el mismo algoritmo. Bueno, ya sabes, como en ese chiste de matemáticas: "Apaga el fuego de la tetera". La tarea se reduce a la anterior.
Intersección de conjuntos
Imagine que estamos tratando de escribir una herramienta para programadores de C ++ que encuentre todas las lambdas en el código con la captura de todas las variables predeterminadas ([=] y [&]) y muestre sugerencias para convertirlas en lambdas con una lista específica de variables capturadas. Algo como esto:
std::partition(begin(elements), end(elements), [=] (auto element) {
En el proceso de analizar el archivo con el código, tendremos que almacenar la colección de variables en algún lugar del alcance actual y circundante, y si se detecta una lambda con la captura de todas las variables, compare estas dos colecciones y brinde consejos sobre su conversión.
Un conjunto con variables en el ámbito primario y otro con variables dentro del lambda. Para formar un consejo, el desarrollador solo necesita encontrar su intersección. Y este es el caso cuando la descripción del algoritmo de STL es perfecta para la tarea:
std :: set_intersection toma dos conjuntos y devuelve su intersección. El algoritmo es hermoso en su simplicidad. Toma dos colecciones ordenadas y las ejecuta en paralelo:
- Si el elemento actual en la primera colección es idéntico al elemento actual en la segunda, agréguelo al resultado y pase a los siguientes elementos en ambas colecciones
- Si el elemento actual en la primera colección es menor que el elemento actual en la segunda colección, vaya al siguiente elemento en la primera colección
- Si el elemento actual en la primera colección es más grande que el elemento actual en la segunda colección, vaya al siguiente elemento en la segunda colección
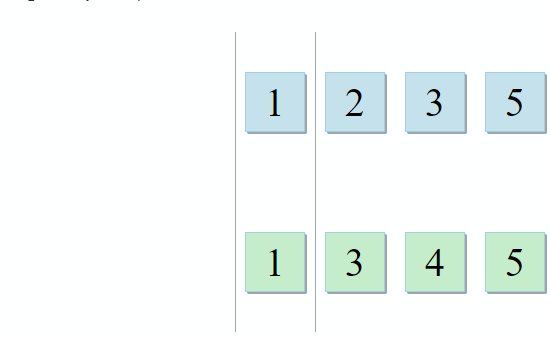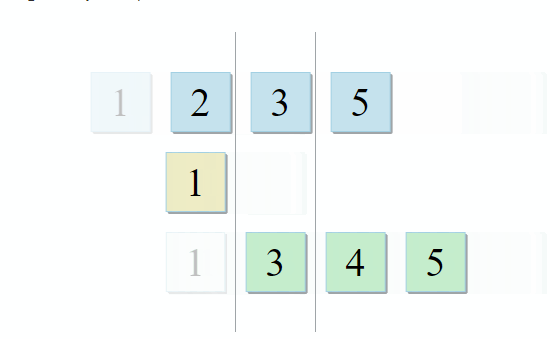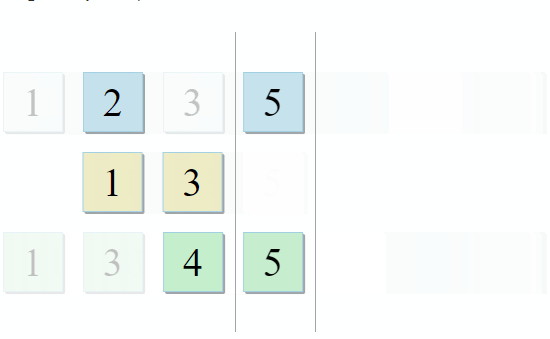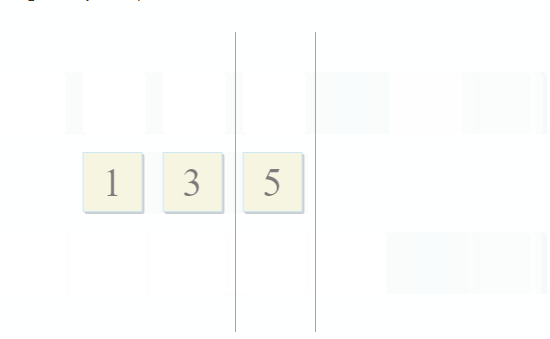
Con cada paso del algoritmo, nos movemos a lo largo de la primera, segunda o ambas colecciones, lo que significa que la complejidad de este algoritmo será lineal: O (m + n), donde n y m son los tamaños de las colecciones.
Simple y efectivo. Pero esto es solo hasta ahora las colecciones de entrada están ordenadas.
Clasificación
El problema es que, en general, las colecciones no están ordenadas. En nuestro caso particular, es conveniente almacenar variables en una estructura de datos similar a una pila agregando variables al siguiente nivel de pila al ingresar un ámbito anidado y eliminarlas de la pila al salir de este ámbito.
Esto significa que las variables no se ordenarán por nombre y no podemos usar directamente std :: set_intersection en sus colecciones. Dado que std :: set_intersection requiere colecciones ordenadas exactamente en la entrada, puede surgir la idea (y a menudo vi este enfoque en proyectos reales) para ordenar colecciones antes de llamar a la función de biblioteca.
Ordenar en este caso eliminará la idea de usar una pila para almacenar variables de acuerdo con su alcance, pero aún así esto es posible:
template <typename InputIt1, typename InputIt2, typename OutputIt> auto unordered_intersection_1(InputIt1 first1, InputIt1 last1, InputIt2 first2, InputIt2 last2, OutputIt dest) { std::sort(first1, last1); std::sort(first2, last2); return std::set_intersection(first1, last1, first2, last2, dest); }
¿Cuál es la complejidad del algoritmo resultante? Algo como O (n log n + m log m + n + m) es la complejidad cuasilineal.
Menos clasificación
¿No podemos usar la clasificación? Podemos, por qué no. Solo buscaremos cada elemento de la primera colección en la segunda búsqueda lineal. Obtenemos la complejidad O (n * m). Y también vi este enfoque en proyectos reales con bastante frecuencia.
En lugar de las opciones "ordenar todo" y "no ordenar nada", podemos intentar encontrar Zen y seguir la tercera vía: clasifique solo una de las colecciones. Si una de las colecciones está ordenada, pero la segunda no, entonces podemos iterar sobre los elementos de la colección sin clasificar uno por uno y buscarlos en la búsqueda binaria ordenada.
La complejidad de este algoritmo será O (n log n) para ordenar la primera colección y O (m log n) para buscar y verificar. En total, obtenemos la complejidad O ((n + m) log n).
Si decidimos ordenar otra de las colecciones, obtenemos la complejidad O ((n + m) log m). Como comprenderá, sería lógico ordenar una colección más pequeña aquí para obtener la complejidad final O ((m + n) log (min (m, n))
La implementación se verá así:
template <typename InputIt1, typename InputIt2, typename OutputIt> auto unordered_intersection_2(InputIt1 first1, InputIt1 last1, InputIt2 first2, InputIt2 last2, OutputIt dest) { const auto size1 = std::distance(first1, last1); const auto size2 = std::distance(first2, last2); if (size1 > size2) { unordered_intersection_2(first2, last2, first1, last1, dest); return; } std::sort(first1, last1); return std::copy_if(first2, last2, dest, [&] (auto&& value) { return std::binary_search(first1, last1, FWD(value)); }); }
En nuestro ejemplo con funciones lambda y captura de variables, la colección que clasificaremos generalmente será la colección de variables utilizadas en el código de la función lambda, ya que es probable que haya menos variables que las variables en el alcance lambda circundante.
Hashing
Y la última opción discutida en este artículo será usar hashing para una colección más pequeña en lugar de ordenarla. Esto nos dará la oportunidad de buscar O (1) en él, aunque la construcción del hash, por supuesto, llevará algún tiempo (de O (n) a O (n * n), lo que puede convertirse en un problema):
template <typename InputIt1, typename InputIt2, typename OutputIt> void unordered_intersection_3(InputIt1 first1, InputIt1 last1, InputIt2 first2, InputIt2 last2, OutputIt dest) { const auto size1 = std::distance(first1, last1); const auto size2 = std::distance(first2, last2); if (size1 > size2) { unordered_intersection_3(first2, last2, first1, last1, dest); return; } std::unordered_set<int> test_set(first1, last1); return std::copy_if(first2, last2, dest, [&] (auto&& value) { return test_set.count(FWD(value)); }); }
El enfoque de hashing será un ganador absoluto cuando nuestra tarea sea comparar constantemente un conjunto pequeño A con un conjunto de otros conjuntos (grandes) B₁, B₂, B ... En este caso, necesitamos construir un hash para A solo una vez, y podemos usar su búsqueda instantánea para compararlo con los elementos de todos los conjuntos B bajo consideración.
Prueba de rendimiento
Siempre es útil confirmar la teoría con la práctica (especialmente en casos como este último, cuando no está claro si los costos iniciales del hashing pagarán con una ganancia en el rendimiento de búsqueda).
En mis pruebas, la primera opción (con la clasificación de ambas colecciones) siempre mostró los peores resultados. Ordenar solo una colección más pequeña funcionó un poco mejor en colecciones del mismo tamaño, pero no demasiado. Pero el segundo y tercer algoritmo mostraron un aumento muy significativo en la productividad (aproximadamente 6 veces) en los casos en que una de las colecciones era 1000 veces más grande que la otra.