Este artículo es una continuación lógica de la introducción de sombreadores de programación para diseñadores de diseño . En él, creamos una plantilla para crear varios efectos bidimensionales con fotos usando sombreadores y observamos un par de ejemplos. En este artículo, agregaremos un par de texturas más, aplicaremos la división Voronoi en la práctica para crear mosaicos a partir de ellos, hablaremos sobre la creación de varias máscaras en sombreadores, sobre pixelación y también tocaremos algunos problemas de la antigua sintaxis GLSL que todavía existe en nuestros navegadores.
Al igual que la última vez, habrá un mínimo de teoría y un máximo de práctica y razonamiento en un lenguaje cotidiano mundano. Los principiantes encontrarán aquí una secuencia de acciones con consejos y notas útiles, y los vendedores frontales experimentados pueden encontrar un par de ideas para inspirarse.
Una encuesta en un artículo anterior mostró que el tema de los efectos de WebGL para los sitios puede ser de interés no solo para las máquinas de escribir, sino también para nuestros colegas de otras especializaciones. Para no confundirlos con las últimas características de ES, nos restringimos deliberadamente a construcciones de sintaxis más tradicionales que todos entienden. Y nuevamente, llamo la atención de los lectores sobre el hecho de que los editores integrados de CodePen afectan el rendimiento de lo que se hace en ellos.
Pero empecemos ...
Plantilla para trabajar con sombreadores
Para aquellos que no han leído el artículo anterior, creamos esta plantilla para trabajar con sombreadores:
En él se crea un plano (en nuestro caso, un cuadrado) en el que se "dibuja" la textura de la imagen. Sin dependencias innecesarias y un sombreador de vértices muy simple. Luego desarrollamos esta plantilla, pero ahora comenzaremos desde el momento en que aún no hay lógica en el sombreador de fragmentos.
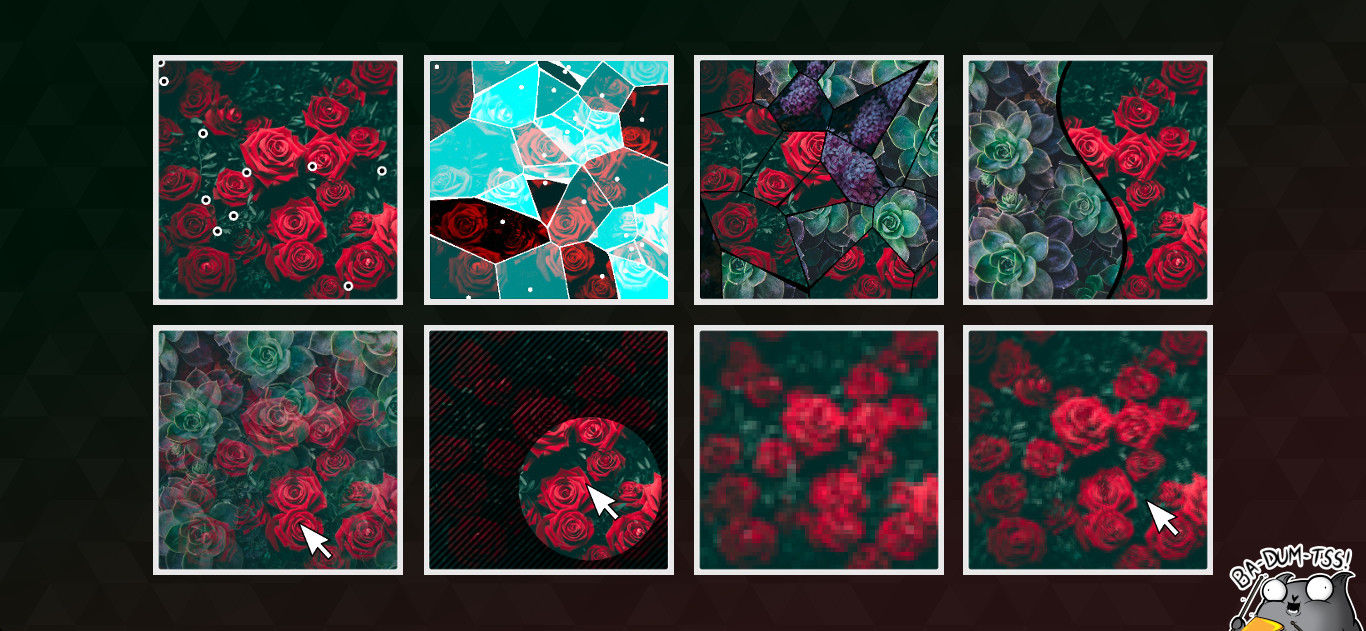
Mosaico
Mosaico es un plano dividido en pequeñas áreas, donde cada una de las áreas se rellena con un determinado color o, como en nuestro caso, textura. ¿Cómo podemos incluso romper nuestro avión en pedazos? Obviamente, puedes dividirlo en rectángulos. Pero esto ya es tan fácil de hacer con la ayuda de SVG, arrastrar WebGL a esta tarea y dejar todo de la nada sin ningún propósito.
Para que el mosaico sea interesante, debe tener diferentes fragmentos, tanto en forma como en tamaño. Hay un enfoque muy simple, pero al mismo tiempo muy entretenido para construir tal partición. Es conocido como el mosaico de Voronoi o la partición de Dirichlet, y en Wikipedia escriben que Descartes usó algo similar en el lejano siglo XVII. La idea es algo como esto:
- Toma un conjunto de puntos en el avión.
- Para cada punto en el plano, encuentre el punto más cercano de este conjunto.
- Eso es todo El plano se divide en áreas poligonales, cada una de las cuales está determinada por uno de los puntos del conjunto.
Probablemente sea mejor mostrar este proceso con un ejemplo práctico. Existen diferentes algoritmos para generar esta partición, pero actuaremos en la frente, porque calcular algo para cada punto en el plano es solo la tarea del sombreador. Primero necesitamos hacer un conjunto de puntos aleatorios. Para no cargar el código de ejemplos, crearemos una variable global para ellos.
function createPoints() { for (let i = 0; i < NUMBER_OF_POINTS; i++) { POINTS.push([Math.random(), Math.random()]); } }
Ahora tenemos que pasarlos a los sombreadores. Los datos son globales, por lo que utilizaremos el modificador uniform . Pero hay un punto sutil: no podemos simplemente pasar una matriz. Parecería que el siglo XXI está en el patio, pero sin embargo no saldrá nada. Como resultado, debe transferir una matriz de puntos uno a la vez.
for (let i = 0; i < NUMBER_OF_POINTS; i++) { GL.uniform2fv(GL.getUniformLocation(PROGRAM, 'u_points[' + i + ']'), POINTS[i]); }
Hoy, a menudo encontraremos problemas similares de inconsistencia entre lo que se espera y lo que está en los navegadores reales. Por lo general, las lecciones de WebGL usan THREE.js y esta biblioteca oculta parte de la suciedad en sí misma, como jQuery alguna vez hizo en sus tareas, pero si la elimina, realmente le duele el cerebro.
En el sombreador de fragmentos, tenemos una variable de matriz para puntos. Solo podemos crear matrices de una longitud fija. Comencemos con 10 puntos:
#define NUMBER_OF_POINTS 10 uniform vec2 u_points[NUMBER_OF_POINTS];
Asegúrese de que todo esto funciona dibujando círculos en los lugares de los puntos. Tal dibujo de varias primitivas geométricas se usa a menudo durante la depuración: son claramente visibles y puede comprender de inmediato qué se encuentra y hacia dónde se mueve.
Use el "dibujo" de círculos, líneas y otros puntos de referencia para los objetos invisibles sobre los que se construyen las animaciones. Esto dará pistas obvias sobre cómo funcionan, especialmente si los algoritmos son complejos de entender rápidamente sin una preparación previa. Luego, todo esto puede comentarse y dejarse en manos de sus colegas: dirán gracias.
for (int i = 0; i < NUMBER_OF_POINTS; i++) { if (distance(texture_coord, u_points[i]) < 0.02) { gl_FragColor = WHITE; break; } }
Bueno Agreguemos también algo de movimiento a los puntos. Para comenzar, deje que se muevan en círculo, luego volveremos a este tema más adelante. Los coeficientes también se ponen en el ojo, solo para ralentizar ligeramente su movimiento y reducir la amplitud de las oscilaciones.
function movePoints(timeStamp) { if (timeStamp) { for (let i = 0; i < NUMBER_OF_POINTS; i++) { POINTS[i][0] += Math.sin(i * timeStamp / 5000.0) / 500.0; POINTS[i][1] += Math.cos(i * timeStamp / 5000.0) / 500.0; } } }
Regresa al sombreador. Para futuros experimentos, encontraremos números útiles de áreas en las que se dividirá todo. Entonces, encontramos el punto más cercano al píxel actual del conjunto y guardamos el número de ese punto: es el número de área.
float min_distance = 1.0; int area_index = 0; for (int i = 0; i < NUMBER_OF_POINTS; i++) { float current_distance = distance(texture_coord, u_points[i]); if (current_distance < min_distance) { min_distance = current_distance; area_index = i; } }
Para probar el rendimiento, nuevamente pintamos todo en colores brillantes:
gl_FragColor = texture2D(u_texture, texture_coord); gl_FragColor.g = abs(sin(float(area_index))); gl_FragColor.b = abs(sin(float(area_index)));
La combinación de módulo (abs) y funciones limitadas (en particular, sin y cos) se utilizan a menudo cuando se trabaja con efectos similares. Por un lado, esto agrega un poco de aleatoriedad, y por otro lado, inmediatamente da un resultado normalizado de 0 a 1, lo cual es muy conveniente: tenemos muchos valores que se encuentran precisamente dentro de estos límites.
También encontraremos puntos más o menos equidistantes de varios puntos del conjunto y los colorearemos. Esta acción no lleva una carga útil especial, pero mirar el resultado sigue siendo interesante.
int number_of_near_points = 0; for (int i = 0; i < NUMBER_OF_POINTS; i++) { if (distance(texture_coord, u_points[i]) < min_distance + EPSILON) { number_of_near_points++; } } if (number_of_near_points > 1) { gl_FragColor.rgb = vec3(1.0); }
Deberías obtener algo como esto:
Esto todavía es un borrador, todavía lo finalizaremos. Pero ahora el concepto general de tal separación del avión es claro.
Mosaico de fotos
Está claro que en su forma pura no hay mucho beneficio de tal partición. Para ampliar tus horizontes y solo por diversión, puedes jugar con él, pero en un sitio real valdría la pena agregar un par de fotos más y hacer un mosaico de ellas. Vamos a rehacer un poco la función de crear texturas, para que haya más de una.
function createTextures() { for (let i = 0; i < URLS.textures.length; i++) { createTexture(i); } } function createTexture(index) { const image = new Image(); image.crossOrigin = 'anonymous'; image.onload = () => { const texture = GL.createTexture(); GL.activeTexture(GL['TEXTURE' + index]); GL.bindTexture(GL.TEXTURE_2D, texture); GL.pixelStorei(GL.UNPACK_FLIP_Y_WEBGL, true); GL.texImage2D(GL.TEXTURE_2D, 0, GL.RGB, GL.RGB, GL.UNSIGNED_BYTE, image); GL.texParameteri(GL.TEXTURE_2D, GL.TEXTURE_WRAP_S, GL.CLAMP_TO_EDGE); GL.texParameteri(GL.TEXTURE_2D, GL.TEXTURE_WRAP_T, GL.CLAMP_TO_EDGE); GL.texParameteri(GL.TEXTURE_2D, GL.TEXTURE_MIN_FILTER, GL.LINEAR); GL.uniform1i(GL.getUniformLocation(PROGRAM, 'u_textures[' + index + ']'), index); }; image.src = URLS.textures[index]; }
No sucedió nada inusual, simplemente reemplazamos los ceros con el parámetro de index y reutilizamos el código existente para cargar las tres texturas. En el sombreador, ahora tenemos una variedad de texturas:
#define NUMBER_OF_TEXTURES 3 uniform sampler2D u_textures[NUMBER_OF_TEXTURES];
Ahora podemos usar el número de área guardado anteriormente para seleccionar una de las tres texturas. Pero ...
Pero antes de eso me gustaría hacer una pequeña digresión. Sobre dolor Sobre la sintaxis. Javascript moderno (condicionalmente ES6 +) es un buen lenguaje. Le permite expresar sus pensamientos a medida que surgen, no limita el marco a ningún paradigma de programación específico, completa algunos puntos para nosotros y le permite centrarse más en la idea que en su implementación. Para el creador, eso es todo. Algunas personas creen que les da demasiada libertad y cambian a TypeScript, por ejemplo. Pure C es un lenguaje más riguroso. También permite mucho, puedes atraer cualquier cosa, pero después de JS se percibe como un poco incómodo, anticuado o algo así. Sin embargo, él todavía es bueno. GLSL tal como existe en los navegadores es simplemente algo. No solo es un orden de magnitud más estricto que C, sino que también carece de muchos operadores familiares y construcciones de sintaxis. Este es probablemente el mayor problema al escribir sombreadores más o menos complejos para WebGL. Detrás del horror en que se convierte el código, puede ser muy difícil echar un vistazo al algoritmo original. Algunos programadores piensan que hasta que aprendan C, el camino hacia los sombreadores está cerrado para ellos. Entonces: el conocimiento de C no ayudará particularmente aquí. Aquí hay una especie de mundo propio. El mundo de la locura, dinosaurios y muletas.
¿Cómo puedo elegir una de las tres texturas que tienen un número? El número de área. El resto viene a la mente dividiendo el número por el número de texturas. Buena idea Solo el operador % , que las manos ya escriben, no está aquí. La impresión de comprender este hecho está bien descrita en la imagen:

Por supuesto, usted dice: "Sí, no hay problema, hay una función de mod , ¡vamos a tomarla!". Pero resulta que ella no acepta dos enteros, solo fracciones. Ok, bueno, haz un float con ellos. También tenemos un float , pero necesitamos un int . Debe volver a convertir todo, de lo contrario, existe una posibilidad no falsa de obtener un error de compilación.
int texture_index = int(mod(float(area_index), float(NUMBER_OF_TEXTURES)))
Y aquí hay una pregunta retórica: ¿tal vez será más fácil realizar su función del resto de la división de enteros que tratar de ensamblarla a partir de métodos estándar? Y esta sigue siendo una función simple, y sucede que se obtienen secuencias muy profundas de tales transformaciones en las que ya no está claro lo que está sucediendo.
Bien, dejémoslo como está por ahora. Simplemente tome el color del píxel deseado de la textura seleccionada y gl_FragColor a la variable gl_FragColor . Entonces? ¿Ya hicimos esto? Y entonces este gato aparece de nuevo. No puede usar una no constante al acceder a una matriz. Y todo lo que calculamos ya no es una constante. Ba-dum-tsss !!!
Tienes que hacer algo como esto:
if (texture_index == 0) { gl_FragColor = texture2D(u_textures[0], texture_coord); } else if (texture_index == 1) { gl_FragColor = texture2D(u_textures[1], texture_coord); } else if (texture_index == 2) { gl_FragColor = texture2D(u_textures[2], texture_coord); }
De acuerdo, dicho código es un camino directo a govnokod.ru , pero no obstante, es diferente de alguna manera. Incluso la switch-case no está aquí para al menos de alguna manera ennoblecer esta desgracia. Realmente hay otra muleta menos obvia que resuelve el mismo problema:
for (int i = 0; i < 3; i++) { if (texture_index == i) { gl_FragColor = texture2D(u_textures[i], texture_coord); } }
Contadores de ciclos, que aumentan en uno, el compilador puede contar como una constante. Pero esto no funcionó con una variedad de texturas: en el último Chrome, apareció un error que decía que era imposible hacer esto con una variedad de texturas. Con una serie de números, funcionó. ¿Adivina por qué funciona con una matriz, pero no con otra? Si pensabas que el sistema de conversión de tipos en JS estaba lleno de magia, ordena el sistema "constante - no constante" en GLSL. Lo curioso es que los resultados también dependen de la tarjeta de video utilizada, por lo que las muletas difíciles que funcionaron en la tarjeta gráfica NVIDIA pueden descomponerse en AMD.
Es mejor evitar tales decisiones basadas en suposiciones sobre el compilador. Tienden a romperse y son difíciles de probar.
La tristeza es tristeza. Pero, si queremos hacer cosas interesantes, necesitamos abstraernos de todo esto y continuar.
Por el momento, tenemos un mosaico de fotos. Pero hay un detalle: si los puntos se acercan mucho, entonces hay una transición rápida de dos áreas. No es muy bonita Debe agregar algún algoritmo que no permita que los puntos se acerquen. Puede hacer una opción simple, en la que se verifican las distancias entre puntos y, si es menor que un cierto valor, los separamos. Esta opción no está exenta de inconvenientes, en particular, a veces conduce a una pequeña contracción de los puntos, pero en muchos casos puede ser suficiente, especialmente porque no hay muchos cálculos aquí. Las opciones más avanzadas serían un sistema de cargas móviles y una "telaraña" en la cual pares de puntos están conectados por resortes invisibles. Si está interesado en implementarlos, puede encontrar fácilmente todas las fórmulas en el libro de referencia de física para la escuela secundaria.
for (let i = 0; i < NUMBER_OF_POINTS; i++) { for (let j = i; j < NUMBER_OF_POINTS; j++) { let deltaX = POINTS[i][0] - POINTS[j][0]; let deltaY = POINTS[i][1] - POINTS[j][1]; let distance = Math.sqrt(deltaX * deltaX + deltaY * deltaY); if (distance < 0.1) { POINTS[i][0] += 0.001 * Math.sign(deltaX); POINTS[i][1] += 0.001 * Math.sign(deltaY); POINTS[j][0] -= 0.001 * Math.sign(deltaX); POINTS[j][1] -= 0.001 * Math.sign(deltaY); } } }
El principal problema con este enfoque, así como con el que usamos en el sombreador, es comparar todos los puntos con todos. No necesita ser un gran matemático para comprender que la cantidad de cálculos de distancia será increíble si no hacemos 10 puntos, sino 1000. Sí, incluso 100 es suficiente para que todo disminuya la velocidad. Por lo tanto, tiene sentido aplicarlo solo para un pequeño número de puntos.
Si queremos hacer un mosaico para una gran cantidad de puntos, entonces podemos usar la división familiar del plano en cuadrados idénticos. La idea es poner un punto en cada cuadrado y luego llevar a cabo todas las comparaciones solo con puntos de cuadrados vecinos. Una buena idea, pero los experimentos han demostrado que con una gran cantidad de puntos, las computadoras portátiles económicas con tarjetas de video integradas aún no pueden hacer frente. Por lo tanto, vale la pena pensar diez veces antes de decidir hacer un mosaico en su sitio a partir de una gran cantidad de fragmentos.
No sean rábanos, verifique el rendimiento de sus artesanías no solo en su granja minera, sino también en computadoras portátiles comunes. Los usuarios serán básicamente los únicos.
Particionar un plano de acuerdo con un gráfico de función
Veamos otra opción para dividir un plano en partes. Ya no requerirá una gran potencia informática. La idea principal es tomar alguna función matemática y construir su gráfica. La línea resultante dividirá el plano en dos partes. Si usamos una función de la forma y = f(x) , obtenemos la división en forma de corte. Reemplazando X con Y, podemos cambiar la sección horizontal a vertical. Si toma la función en coordenadas polares, entonces necesita traducir todo al cartesiano y viceversa, pero la esencia de los cálculos no cambiará. En este caso, el resultado no es un corte en dos partes, sino un corte de agujero. Pero veremos la primera opción.
Para cada Y, calcularemos el valor de X para hacer una sección vertical. Podríamos tomar una onda sinusoidal para estos fines, por ejemplo, pero es demasiado aburrido. Es mejor tomar algunas piezas a la vez y doblarlas.
Tomamos varias sinusoides, cada una de las cuales está vinculada a una coordenada a lo largo de Y y al tiempo, y las sumamos. Los físicos llamarían a esta adición superposición. Obviamente, multiplicando el resultado completo por algún número, cambiamos la amplitud. Sácalo en una macro separada. Si multiplica la coordenada, el parámetro seno, la frecuencia cambiará. Ya hemos visto esto en un artículo anterior. También eliminamos el modificador de frecuencia común a todos los sinusoides de la fórmula. No será superfluo jugar con el tiempo, un signo negativo dará el efecto de mover la línea en la dirección opuesta.
float time = u_time * SPEED; float x = (sin(texture_coord.y * FREQUENCY) + sin(texture_coord.y * FREQUENCY * 2.1 + time) + sin(texture_coord.y * FREQUENCY * 1.72 + time * 1.121) + sin(texture_coord.y * FREQUENCY * 2.221 + time * 0.437) + sin(texture_coord.y * FREQUENCY * 3.1122 + time * 4.269)) * AMPLITUDE;
Habiendo hecho tales ajustes globales para nuestra función, enfrentaremos el problema de repetir el mismo movimiento a intervalos bastante cortos. Para resolver este problema, necesitamos multiplicar todo por coeficientes para los cuales el múltiplo común más pequeño es muy grande. Algo similar también se usa en el generador de números aleatorios, ¿recuerdas? En este caso, no pensamos y tomamos números ya preparados de algún ejemplo de Internet, pero nadie se molesta en experimentar con nuestros valores.
Solo queda elegir una de las dos texturas para los puntos por encima de nuestro gráfico de funciones y la segunda para los puntos debajo de ella. Más precisamente a izquierda y derecha, todos giramos:
if (texture_coord.x - 0.5 > x) { gl_FragColor = texture2D(u_textures[0], texture_coord); } else { gl_FragColor = texture2D(u_textures[1], texture_coord); }
Lo que recibimos se parece a las ondas sonoras. Más precisamente, su imagen en el osciloscopio. De hecho, podríamos, en lugar de nuestros sinusoides, transmitir datos desde algún tipo de archivo de sonido. Pero trabajar con sonido es un tema para un artículo separado.
Mascaras
Los ejemplos anteriores deberían llevar a un comentario bastante lógico: todo esto se parece al trabajo de las máscaras en SVG (si no ha trabajado con ellas, vea ejemplos del artículo Máscaras SVG y efectos wow ). Es solo que aquí los hacemos un poco diferente. Y el resultado es el mismo: algunas áreas están pintadas con una textura, otras con otra. Solo las transiciones suaves aún no han sido. Así que hagamos uno.
Eliminamos todo lo innecesario y devolvemos las coordenadas del mouse. Haga un degradado radial con el centro en la ubicación del cursor y úselo como máscara. En este ejemplo, el comportamiento del sombreador se parecerá más a la lógica de las máscaras en SVG que en los ejemplos anteriores. Necesitamos una función de mix y alguna función de distancia. El primero mezclará los valores de color de píxel de ambas texturas, tomando como tercer parámetro un coeficiente (de 0 a 1) que determina cuál de los valores prevalecerá como resultado. Tomamos el módulo seno en función de la distancia; solo dará un cambio suave en el valor entre 0 y 1.
gl_FragColor = mix( texture2D(u_textures[0], texture_coord), texture2D(u_textures[1], texture_coord), abs(sin(length(texture_coord - u_mouse_position / u_canvas_size))))
Eso es todo Veamos el resultado:
La principal ventaja sobre SVG es obvia:
A diferencia de SVG, aquí podemos hacer fácilmente gradientes suaves para diversas funciones matemáticas, y no recopilarlos de muchos gradientes lineales.
Si tiene una tarea más simple que no requiere transiciones suaves o formas complejas que se calculan en el proceso, lo más probable es que sea más fácil de implementar sin el uso de sombreadores. Sí, y es probable que el rendimiento en hardware débil sea mejor. Elija una herramienta basada en sus tareas.
Para fines educativos, veamos otro ejemplo. Primero, haz un círculo en el que la textura permanecerá como está:
gl_FragColor = texture2D(u_textures[0], texture_coord); float dist = distance(texture_coord, u_mouse_position / u_canvas_size); if (dist < 0.3) { return; }
Y rellena el resto con rayas diagonales:
float value = sin((texture_coord.y - texture_coord.x) * 200.0); if (value > 0.0) { gl_FragColor.rgb *= dist; } else { gl_FragColor.rgb *= dist / 10.0; }
Las aceptaciones son las mismas: multiplicamos el parámetro para el seno para aumentar la frecuencia de las rayas; dividir los valores obtenidos en dos partes; Para cada una de las mitades, transformamos el color de los píxeles a nuestra manera. Es útil recordar que dibujar líneas diagonales generalmente se asocia con la adición de coordenadas en X e Y. Tenga en cuenta que también usamos la distancia al cursor del mouse cuando cambiamos los colores, creando así una especie de sombra. De la misma manera, puede usarlo con transformaciones geométricas, pronto veremos esto en el ejemplo de pixelación. Mientras tanto, mira el resultado de este sombreador:
Simple y bonita
Y sí, si se confunde un poco, puede crear texturas no a partir de imágenes, sino a partir de cuadros de videos (hay muchos ejemplos en la red, puede resolverlos fácilmente) y aplicarles todos nuestros efectos. Muchos sitios de directorio como Awwwards usan estos efectos junto con el video.
Vale la pena recordar un pensamiento más:
Nadie se molesta en usar una de las texturas como máscara. Podemos tomar una foto y usar los valores de color de sus píxeles en nuestras transformaciones, ya sea cambios en otros colores, cambios a los lados o algo más que se te ocurra.
Pero volvamos a dividir el avión en partes.
Pixelización
Este efecto es algo obvio, pero al mismo tiempo es tan común que sería un error pasar por alto. Divida nuestro plano en cuadrados, de la misma manera que en el ejemplo con el generador de ruido, y luego para todos los píxeles dentro de cada cuadrado establecemos el mismo color. Se obtiene mezclando valores de las esquinas de un cuadrado, ya hicimos algo similar. Para este efecto, no necesitamos fórmulas complejas, así que solo suma todos los valores y divide entre 4, el número de ángulos del cuadrado.
float block_size = abs(sin(u_time)) / 20.0; vec2 block_position = floor(texture_coord / block_size) * block_size; gl_FragColor = ( texture2D(u_textures[0], block_position) + texture2D(u_textures[0], block_position + vec2(1.0, 0.0) * block_size) + texture2D(u_textures[0], block_position + vec2(0.0, 1.0) * block_size) + texture2D(u_textures[0], block_position + vec2(1.0, 1.0) * block_size) ) / 4.0;
Nuevamente vinculamos uno de los parámetros al tiempo a través del módulo seno para ver visualmente qué sucede cuando cambia.
Olas de píxeles
, .
float block_size = abs(sin( length(texture_coord - u_mouse_position / u_canvas_size) * 2.0 - u_time)) / 100.0 + 0.001;
, 0 1; , , , . , .
"" , , -. . " ", , . . — . .
Resumen
, , , , . -. - - . . . , , , .
PS: , WebGL ( ) ? , , . ?