Continuamos nuestro ciclo sobre el dispositivo blockchain de Monero, y el artículo de hoy estará dedicado al protocolo RingCT (Ring Confidential Transactions), que presenta transacciones confidenciales y nuevas firmas de anillo. Desafortunadamente, hay poca información en Internet sobre cómo funciona, y tratamos de llenar este vacío.

Hablaremos sobre cómo la red oculta la cantidad de transferencias utilizando este protocolo, por qué rechazamos las firmas de anillo clásicas para cryptonote y cómo esta tecnología se desarrollará aún más.
Dado que este protocolo es una de las tecnologías más complejas en Monero, el lector necesitará conocimientos básicos sobre el dispositivo de esta cadena de bloques y conocimientos superficiales en criptografía en curvas elípticas (para actualizar este conocimiento, puede leer los primeros capítulos de nuestro artículo anterior sobre
firmas múltiples ).
Protocolo RingCT
Uno de los posibles ataques a las monedas cryptonote es el análisis de blockchain basado en el conocimiento de la cantidad y el tiempo de la transacción enviada. Permite
reduzca significativamente la búsqueda de los resultados de interés para el atacante. Para protegerse contra dicho análisis, Monero introdujo un protocolo de transacción anónimo que oculta por completo la cantidad de transferencias en la red.
Vale la pena señalar que la idea de ocultar cantidades no es nueva. Uno de los primeros en describirlo fue el desarrollador de Bitcoin Core Greg Maxwell en su
artículo de Transacciones confidenciales . La implementación actual de RingCT es su modificación con la posibilidad de usar firmas de anillo (sin ellas), y así obtuvo su nombre: Transacciones confidenciales de anillo.
Entre otras cosas, el protocolo ayuda a deshacerse de los problemas con la mezcla de salidas de polvo: salidas por una pequeña cantidad (generalmente obtenida en forma de cambio de las transacciones), lo que creó más problemas de lo que ellos mismos cuestan.
En enero de 2017, se llevó a cabo la red de hard fork de Monero, lo que permitió el uso opcional de transacciones confidenciales. Y en septiembre de ese año, con la versión 6 hard fork, tales transacciones se convirtieron en las únicas permitidas en la red.
RingCT utiliza varios mecanismos a la vez: firmas de grupos anónimos espontáneos enlazables de varias capas (en lo sucesivo, MLSAG), compromisos de Pedersen y pruebas de rango (este término no tiene traducción establecida al ruso).
El protocolo RingCT introduce dos tipos de transacciones anónimas: simples y completas. La primera billetera se genera cuando una transacción usa más de una entrada, la segunda, en la situación opuesta. Difieren en la validación de los montos de las transacciones y los datos firmados por la firma MLSAG (hablaremos más sobre esto a continuación). Además, las transacciones de tipo completo se pueden generar con cualquier número de entradas, no hay una diferencia fundamental. El libro
"Cero para Monero" sobre este tema dice que la decisión de limitar las transacciones completas a una entrada se hizo con prisa y puede cambiar en el futuro.
Firma MLSAG
Recordemos cuáles son las entradas firmadas de una transacción. Cada transacción gasta algo de dinero y genera. Los fondos se generan creando salidas de transacciones (una analogía directa son los billetes), y la salida que gasta una transacción (porque en la vida real gastamos dinero en billetes) se convierte en una entrada (con cuidado, es muy fácil confundirse aquí).
La entrada se refiere a varias salidas, pero gasta solo una, creando así una "pantalla de humo" para dificultar el análisis de la historia de las traducciones. Si una transacción tiene más de una entrada, dicha estructura se puede representar en forma de matriz, donde las filas son entradas y las columnas son salidas de amasado. Para demostrar a la red que la transacción gasta sus salidas (conoce sus claves secretas), las entradas se firman con una firma de anillo. Dicha firma garantiza que el firmante conocía las claves secretas de todos los elementos de cualquiera de las columnas.
Las transacciones confidenciales ya no usan las firmas de anillo de
criptonota clásicas, sino que han sido reemplazadas por MLSAG, una versión de entrada múltiple de las firmas de anillo similares de una sola capa,
LSAG .
Se llaman de varias capas porque firman varias entradas a la vez, cada una de las cuales se mezcla con varias otras, es decir, se firma una matriz, no una fila. Como veremos más adelante, esto ayuda a ahorrar en el tamaño de la firma.
Veamos cómo se forma una firma de anillo, usando el ejemplo de una transacción que gasta 2 salidas reales y usa m - 1 al azar de blockchain para amasar. Denote las claves públicas de los resultados que gastamos como
, e imágenes clave para ellos respectivamente:
Por lo tanto, obtenemos una matriz de
2 x m . Primero, necesitamos calcular los llamados desafíos para cada par de salidas:
Comenzamos los cálculos con los resultados que gastamos usando sus claves públicas:
y números aleatorios
Como resultado, obtenemos los valores:
que usamos para calcular el desafío
el siguiente par de resultados (para que sea más fácil entender dónde estamos sustituyendo, resaltamos estos valores en diferentes colores). Todos los siguientes valores se calculan en un círculo de acuerdo con las fórmulas dadas en la primera ilustración. El desafío para un par de salidas reales se calcula en último lugar.
Como podemos ver, en todas las columnas, excepto la que contiene las salidas reales, se utilizan números generados aleatoriamente
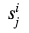
. Para la columna π, también los necesitamos. Convertir
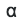
en s:
La firma en sí es una tupla de todos estos valores:
Además, estos datos se escriben en la transacción.
Como podemos ver, MLSAG contiene solo un desafío
c 0 , que ahorra en el tamaño de la firma (que ya requiere mucho espacio). Luego, cualquier revisor que use los datos
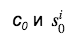
, restaura los valores c
1 , ..., c
m y verifica que

. Por lo tanto, nuestro anillo se cerró y la firma pasó la verificación.
Para las transacciones RingCT de tipo completo, se agrega una línea más a la matriz con salidas mixtas, pero hablaremos de esto a continuación.
Compromisos de Pedersen
Los esquemas de compromiso (a menudo usan el término en inglés: compromisos) se utilizan para que un lado pueda probar que conoce un cierto secreto (número), sin revelarlo realmente. Por ejemplo, arroja un cierto número en los huesos, considera el compromiso y se lo pasa a la parte que confía. Por lo tanto, al momento de revelar el número secreto, el inspector considera independientemente el compromiso, asegurándose de que no lo haya engañado.
Los compromisos de Monero se utilizan para ocultar la cantidad de transferencias y utilizan la opción más común: los compromisos de Pedersen. Por cierto, un hecho curioso: al principio, los desarrolladores sugirieron ocultar las cantidades con el amasamiento habitual, es decir, agregar salidas a cantidades arbitrarias para introducir incertidumbre, pero luego cambiaron a compromisos (no el hecho de que ahorraron en el tamaño de la transacción, como veremos a continuación).
En general, el compromiso es el siguiente:
Donde
C es el valor del compromiso en sí,
a es la cantidad que debe ocultarse,
H es el punto fijo en la curva elíptica (generador adicional) y
x es una máscara arbitraria que oculta el factor generado aleatoriamente. Aquí se necesita la máscara para que el tercero no pueda seleccionar el valor del compromiso con una simple fuerza bruta.
Al generar una nueva salida, la billetera calcula un compromiso y, al gastarla, toma el valor calculado durante la generación o lo vuelve a contar, según el tipo de transacción.
Ringct simple
En el caso de transacciones simples de RingCT, para garantizar que la transacción haya creado salidas iguales a la suma de las entradas (no ganó dinero desde el aire), los compromisos de la primera y la segunda deben ser los mismos, es decir:
Las comisiones de compromiso consideran un poco diferente, sin una máscara:
, donde
a es el importe de la comisión, está disponible públicamente.
Este enfoque nos permite demostrarle a la parte que confía que usamos las mismas cantidades sin revelarlas.
Para aclarar las cosas, veamos un ejemplo. Suponga que una transacción gasta dos salidas (es decir, se convierten en entradas) en 10 y 5 XMR y genera tres salidas por un total de 12 XMR: 3, 4 y 5 XMR. Al mismo tiempo paga una comisión de 3 XMR. Por lo tanto, la cantidad de dinero gastado más la cantidad generada y la comisión es igual a 15 XMR. Tratemos de calcular los compromisos y observemos la diferencia en sus montos (recuerde las matemáticas):
Aquí vemos que la ecuación converge: las sumas de las máscaras de las entradas y salidas que necesitamos son las mismas. Para hacer esto, la billetera genera aleatoriamente
x 1 , y 1 , y 2 e y 3 , y el
x 2 restante calcula de esta manera:
Con estas máscaras, podemos demostrar a cualquiera que verifique que no generamos más fondos de los que gastamos sin revelar el monto. Original, ¿verdad?
RingCT lleno
En las transacciones completas de RingCT, verificar la cantidad de transferencias es algo más complejo. En estas transacciones, la billetera no cuenta los compromisos para las entradas, sino que usa los calculados cuando se generan. En este caso, debemos suponer que la diferencia en las cantidades que ya no tenemos es igual a cero, sino que:
Aquí
z es la diferencia entre las máscaras de las entradas y salidas. Si consideramos
zG como una clave pública (que es de facto), entonces
z es una clave privada. Por lo tanto, conocemos las claves públicas y privadas correspondientes. Con estos datos, podemos usarlos en la firma del anillo MLSAG junto con las claves públicas de las salidas de amasado:
Por lo tanto, una firma de anillo válida garantizará que conozcamos todas las claves privadas de una de las columnas, y solo podemos conocer la clave privada en la última fila si la transacción no genera más fondos de los que gasta. Por cierto, aquí está la respuesta a la pregunta "¿por qué la diferencia en las cantidades de los compromisos no conducen a cero"? Si
zG = 0 , entonces
abriremos la columna con resultados reales.
Pero, ¿cómo sabe el destinatario cuánto dinero le enviaron? Aquí todo es simple: el remitente de la transacción y el destinatario intercambian claves utilizando el protocolo Diffie-Hellman, utilizando la clave de transacción y la clave de visualización del destinatario, y calculan el secreto compartido. El remitente escribe en los campos especiales de los datos de la transacción en las sumas de las salidas cifradas con esta clave compartida.
Pruebas de rango
Pero, ¿qué sucede si usa un número negativo como la cantidad en los compromisos? ¡Esto puede conducir a la generación de monedas adicionales! Tal resultado es inaceptable, por lo tanto, necesitamos una garantía de que las cantidades que usamos no son negativas (sin revelar estas cantidades, por supuesto, de lo contrario es mucho trabajo y todo en vano). En otras palabras, debemos demostrar que la suma está en el intervalo
[0, 2 n - 1] .
Para esto, la suma de cada salida se divide en dígitos binarios y el compromiso para cada dígito se considera por separado. Cómo sucede esto, es mejor considerar un ejemplo.
Supongamos que tenemos pequeñas cantidades y ajustamos 4 bits (en la práctica, esto es 64 bits), y creamos una salida para la cantidad de 5 XMR. Consideramos compromisos para cada categoría y un compromiso general para el monto total:
A continuación, cada compromiso se mezcla con un sustituto
(C i -2 i H) y se firma en pares con la firma del anillo Borromeo (otra firma del anillo) propuesta por Greg Maxwell en 2015 (puede encontrar más información al respecto
aquí ):
Juntos, esto se llama prueba de rango y garantiza que los compromisos usen cantidades en el intervalo
[0, 2 n - 1] .
Que sigue
En la implementación actual, las pruebas de rango ocupan mucho espacio: 6176 bytes por salida. Esto lleva a grandes transacciones y, en consecuencia, mayores comisiones. Para reducir el tamaño de la transacción de Monero, los desarrolladores están introduciendo en lugar de las firmas de Borromeo a prueba de balas, un mecanismo de prueba de rango sin compromisos bit a bit.
Según algunas estimaciones , pueden reducir el tamaño de prueba de rango al 94%. Por cierto, a mediados de julio, la tecnología fue
auditada por Kudelski Security, que no reveló ninguna deficiencia significativa en la tecnología en sí o en su implementación. La tecnología ya se usa en la red de prueba, y con el nuevo hard fork, probablemente se pueda mover a la red principal.
Haga sus preguntas, sugiera temas para nuevos artículos sobre tecnologías de criptomonedas y suscríbase a nuestro grupo en
Facebook para mantenerse al tanto de nuestros eventos y publicaciones.