Geekly articles weekly

Ordenar por selección



¿Cuál es la idea de ordenar por elección?

  1. En una submatriz sin clasificar, se busca un máximo local (mínimo).
  2. El máximo (mínimo) encontrado cambia de lugar con el último (primer) elemento en la submatriz.
  3. Si las submatrices sin clasificar permanecen en la matriz, consulte el punto 1.

Una ligera digresión lírica. Inicialmente, en mi serie de artículos, planeaba presentar constantemente material sobre clases de clasificación en un orden estricto. Después de la clasificación de la biblioteca , se planearon artículos sobre otros algoritmos de inserción: clasificación de solitario, clasificación por una tabla Young, clasificación por inversión, etc.

Sin embargo, ahora la tendencia es no lineal, por lo tanto, sin escribir todas las publicaciones sobre la clasificación por insertos, hoy comenzaré una rama paralela sobre la clasificación por selección. Luego haré lo mismo para otras clases algorítmicas: fusionar clases, distribuir clases, etc. Esto generalmente permitirá que se publiquen publicaciones sobre un tema y luego sobre otro. Con una rotación tan temática será más divertido.

Tipo de selección




Simple y sin pretensiones: revisamos la matriz en busca del elemento máximo. El máximo encontrado se intercambia con el último elemento. La parte no ordenada de la matriz disminuyó en un elemento (no incluye el último elemento donde reorganizamos el máximo encontrado). Aplicamos las mismas acciones a esta parte no ordenada: encontramos el máximo y lo colocamos en el último lugar en la parte no ordenada de la matriz. Y así continuamos hasta que la parte no ordenada de la matriz se reduzca a un elemento.

def selection(data): for i, e in enumerate(data): mn = min(range(i, len(data)), key=data.__getitem__) data[i], data[mn] = data[mn], e return data


Ordenar con una simple elección es una doble búsqueda aproximada. ¿Se puede mejorar? Veamos algunas modificaciones.

Doble selección de clasificación :: Doble selección de clasificación




Una idea similar se utiliza en la clasificación de agitadores , que es una variante de la clasificación de burbujas. Al pasar por la parte no ordenada de la matriz, además del máximo, también encontramos simultáneamente el mínimo. Ponemos el mínimo en primer lugar, el máximo en el último. Por lo tanto, la parte sin clasificar en cada iteración se reduce en dos elementos a la vez.

A primera vista, parece que esto acelera el algoritmo 2 veces: después de cada pasada, el subconjunto sin clasificar se reduce no de uno, sino de dos lados a la vez. Pero al mismo tiempo, el número de comparaciones aumentó 2 veces, y el número de intercambios se mantuvo sin cambios. La selección doble solo aumenta ligeramente la velocidad del algoritmo, y en algunos idiomas incluso funciona más lento por alguna razón.

La diferencia entre ordenar por elección de ordenar por inserción


Puede parecer que ordenar por selección y ordenar por inserciones es una misma cosa, una clase común de algoritmos. Bueno, o ordenar por insertos es un tipo de clasificación por elección. O la clasificación por elección es un caso especial de clasificación por insertos. Y allí y allá, nos turnamos desde la parte no ordenada de la matriz para extraer los elementos y redirigirlos al área ordenada.

La principal diferencia: al ordenar por inserciones, extraemos cualquier elemento de la parte no ordenada de la matriz y lo insertamos en su lugar en la parte ordenada. En la ordenación por selección, buscamos a propósito el elemento máximo (o mínimo) con el que complementamos la parte ordenada de la matriz. En las inserciones que estamos buscando dónde insertar el siguiente elemento, y en la elección, ya sabemos de antemano qué lugar colocaremos, pero al mismo tiempo necesitamos encontrar el elemento que corresponde a este lugar.

Esto hace que ambas clases de algoritmos sean completamente diferentes entre sí en su esencia y los métodos utilizados.

Bingo sort :: Bingo sort


Una característica interesante de las opciones de clasificación es la independencia de la velocidad de la naturaleza de los datos que se ordenan.

Por ejemplo, si la matriz está casi ordenada, entonces, como sabe, la ordenación por inserciones la procesará mucho más rápido (incluso más rápido que la ordenación rápida). Una matriz de orden inverso para ordenar por inserciones es un caso degenerado, lo ordenará el mayor tiempo posible.

Y para ordenar por selección, el ordenamiento parcial o inverso de la matriz no juega un papel: lo procesará aproximadamente a la misma velocidad que uno aleatorio regular. Además, para la clasificación clásica, no importa si la matriz consta de elementos únicos o repetitivos, esto prácticamente no afecta la velocidad.

Pero, en principio, puede idear y modificar el algoritmo para que funcione más rápido con algunos conjuntos de datos. Por ejemplo, la ordenación del bingo tiene en cuenta si la matriz consiste en elementos repetitivos.



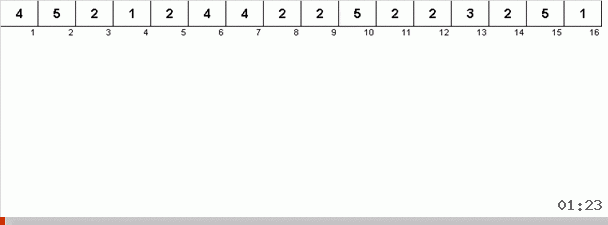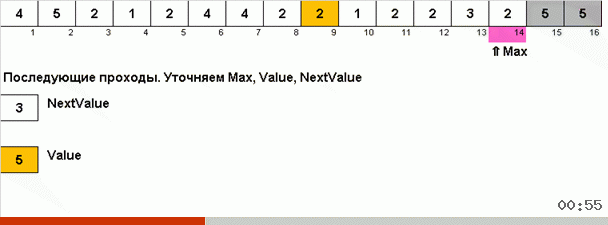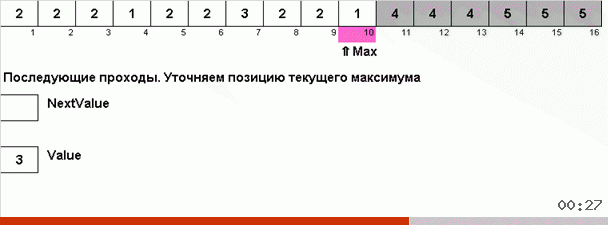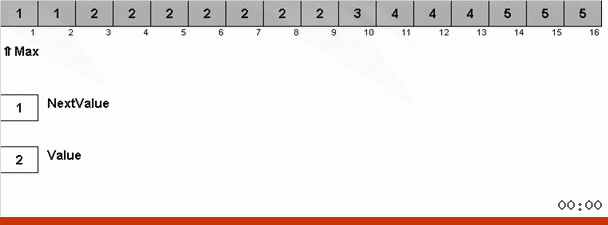
El truco aquí es que no solo se recuerda el elemento máximo en la parte desordenada, sino que también se determina el máximo para la próxima iteración. Esto permite que los máximos repetidos no los busquen nuevamente cada vez, sino que los coloquen en su lugar tan pronto como este máximo se encuentre nuevamente en la matriz.

La complejidad algorítmica se mantuvo igual. Pero si la matriz consiste en números repetitivos, entonces la clasificación del bingo funcionará diez veces más rápido que la clasificación normal por elección.

 # - def bingo(data): #  . max = len(data) - 1 nextValue = data[max] for i in range(max - 1, -1, -1): if data[i] > nextValue: nextValue = data[i] while max and data[max] == nextValue: max -= 1 #  . while max: value = nextValue nextValue = data[max] for i in range(max - 1, -1, -1): if data[i] == value: data[i], data[max] = data[max], data[i] max -= 1 elif data[i] > nextValue: nextValue = data[i] while max and data[max] == nextValue: max -= 1 return data


Ciclo de clasificación :: Ciclo de clasificación


La ordenación en bucle es interesante (y valiosa desde un punto de vista práctico) ya que los cambios entre los elementos de la matriz ocurren si y solo si el elemento se coloca en su lugar final. Esto puede ser útil si la reescritura en una matriz es demasiado costosa y cuidar la memoria física requiere minimizar el número de cambios en los elementos de la matriz.



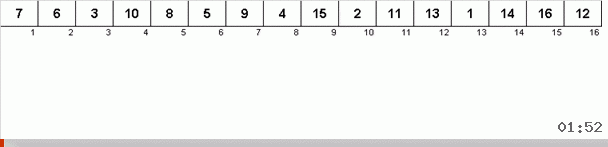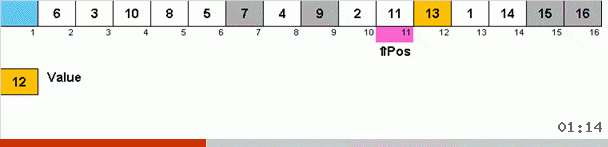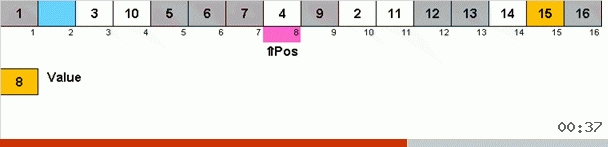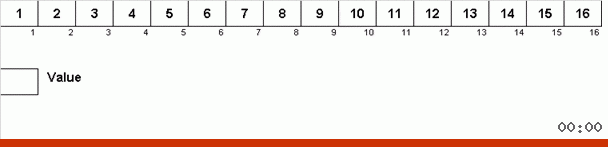
Funciona asi. Ordenamos la matriz, llamamos a X la siguiente celda de este bucle externo. Y observamos qué lugar en la matriz necesitamos para insertar el siguiente elemento de esta celda. En el lugar donde desea pegar se encuentra otro elemento, lo enviamos al portapapeles. Para este elemento en el búfer, también buscamos su lugar en la matriz (y lo pegamos en este lugar, y enviamos al búfer el elemento que aparece en este lugar). Y para el nuevo número en el búfer, realizamos las mismas acciones. ¿Cuánto tiempo debe continuar este proceso? Hasta que el siguiente elemento en el portapapeles resulte ser el elemento que debe insertarse con precisión en la celda X (el lugar actual en la matriz en el bucle principal del algoritmo). Tarde o temprano, este momento sucederá y luego, en el bucle externo, puede ir a la siguiente celda y repetir el mismo procedimiento.

En otros tipos, por elección, buscamos máximo / mínimo para ponerlos en último / primer lugar. En la ordenación por ciclo, resulta que al menos el primer lugar en la submatriz se encuentra, por así decirlo, en el proceso de cómo se colocan otros elementos en el lugar que les corresponde en algún lugar en el medio de la matriz.

Y aquí, la complejidad algorítmica también permanece dentro de O ( n 2 ). En la práctica, la ordenación cíclica funciona incluso varias veces más lentamente que la ordenación regular por elección, ya que tiene que recorrer la matriz más y comparar más a menudo. Este es el precio por el menor número posible de reescrituras.

 #   def cycle(data): #        for cycleStart in range(0, len(data) - 1): value = data[cycleStart] # ,    pos = cycleStart for i in range(cycleStart + 1, len(data)): if data[i] < value: pos += 1 #      ,   #      if pos == cycleStart: continue #   ,     #        while value == data[pos]: pos += 1 data[pos], value = value, data[pos] #      , #         while pos != cycleStart: # ,    pos = cycleStart for i in range(cycleStart + 1, len(data)): if data[i] < value: pos += 1 #      #      while value == data[pos]: pos += 1 data[pos], value = value, data[pos] return data


Pancake Sort


Un algoritmo que ha dominado todos los niveles de la vida, desde bacterias hasta Bill Gates .



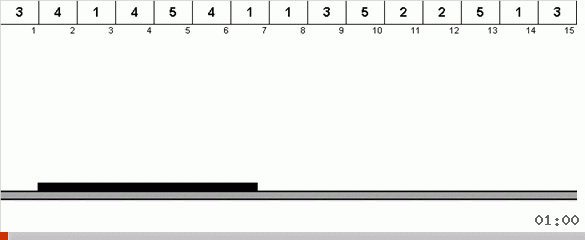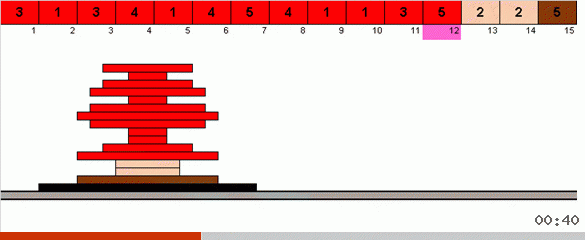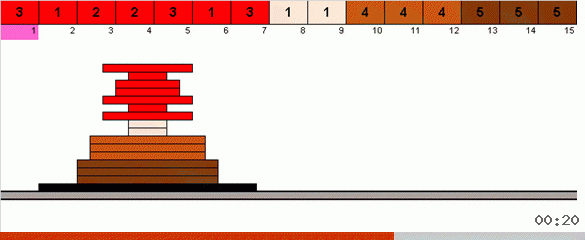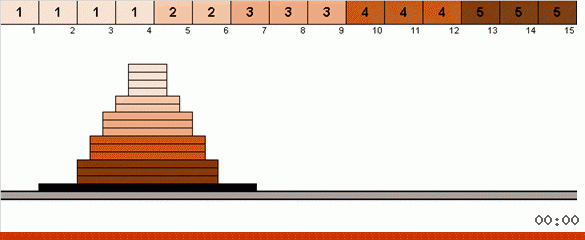
En el caso más simple, estamos buscando el elemento máximo en la parte no ordenada de la matriz. Cuando se encuentra el máximo, hacemos dos giros bruscos. Primero, giramos la cadena de elementos para que el máximo esté en el extremo opuesto. Luego volcamos todo el subconjunto sin clasificar, como resultado de lo cual el máximo cae en su lugar.

Tales cordillets, en general, conducen a una complejidad algorítmica en O ( n 3 ). Estos ciliados entrenados están cayendo de un solo golpe (por lo tanto, en su ejecución la complejidad es O ( n 2 )), y cuando se programa, la inversión de parte de la matriz es un ciclo adicional.

La clasificación de panqueques es muy interesante desde un punto de vista matemático (las mejores mentes estaban pensando en evaluar el número mínimo de vueltas suficientes para la clasificación), hay formulaciones más complejas del problema (con el supuesto lado quemado). El tema de los panqueques es extremadamente interesante, tal vez escribiré una monografía más completa sobre estos temas.

 #   def pancake(data): if len(data) > 1: for size in range(len(data), 1, -1): #      maxindex = max(range(size), key = data.__getitem__) if maxindex + 1 != size: #    ,    if maxindex != 0: #  , #     data[:maxindex+1] = reversed(data[:maxindex+1]) #    , #      data[:size] = reversed(data[:size]) return data



La ordenación por selección es tan efectiva como la búsqueda del elemento mínimo / máximo en la parte no ordenada de la matriz. En todos los algoritmos analizados hoy, la búsqueda se realiza en forma de doble búsqueda. Y en la búsqueda doble, digamos lo que se diga, la complejidad algorítmica siempre no será mejor que O ( n 2 ). ¿Significa esto que todas las clasificaciones por elección están destinadas a significar complejidad cuadrada? En absoluto, si el proceso de búsqueda se organiza de una manera fundamentalmente diferente. Por ejemplo, considere un conjunto de datos como un montón y busque en el montón. Sin embargo, el tema de los montones ni siquiera es un artículo, sino una saga completa, definitivamente hablaremos de montones, sino en otra ocasión.

Referencias


Selección / Ciclo , Panqueque / Panqueques

Artículos de la serie:



El bingo, el ciclo y el panqueque de hoy se han agregado a la aplicación AlgoLab. En el último, en relación con el dibujo de panqueques, se ha establecido una restricción: los valores de los elementos en la matriz deben ser del 1 al 5. Por supuesto, puede poner más, pero las macros tomarán números al azar de este rango.

Source: https://habr.com/ru/post/es422085/

More articles:


All Articles